运用“等效碰撞”解题 提升模型拓展能力

王利东 姜连国

（1.首都师范大学附属苹果园中学，北京 100144；2.北京市第八十中学，北京 100102）

1 引言

2017年版高中物理课程标准强调物理学科的核心素养，更加重视学生科学思维和科学探究的培养.新课标对物理建模能力提出了明确的要求，在物理学科的核心素养中，模型建构是科学思维的重要组成部分，要求学生基于经验事实建构物理模型，运用抽象概括、分析综合、推理论证等科学方法，基于事实证据和科学推理对不同观点和结论提出质疑和批判，进行检验和修正，进而提出创造性见解.物理模型是物理知识的主要成分，物理建模是学生建构和使用物理知识、进而认识真实世界的过程.在物理建模活动中，学习者必须根据已有的物理知识和生活经验，使用所给予的材料和工具来探究面对的新情境，建构起对当前情境的理解，并将自己的这种理解表达出来.

碰撞是动量和守恒部分的重要模型，涉及到动量和能量的知识.这一部分内容综合性强，从经典碰撞模型的建立，到模型的应用和拓展，都对学生提出了较高的要求.新课标对不同层次的学业水平作出了细致的描述，其中水平4是高考要求达到的层次.在水平4对建模能力的描述中，要求“能将实际问题中的对象和过程转换成所学的物理模型”，在实际问题和过程中抽象物理模型，建模情境更复杂，难度更高；要求“能对综合性物理问题进行分析和推理，获得结论并作出解释”，模型优化更全面，综合性更高；要求“能恰当使用证据证明物理结论”明确提出论证需要，不仅要明确观点，还要指出理由；要求“能对已有结论提出有依据的质疑，采用不同方式分析解决物理问题”，通过运用类比迁移、质疑创新等高阶思维，实现物理模型的拓展和推广.［1］

高考对碰撞模型的考查不仅局限于经典模型的提取，还常常涉及到碰撞模型在不同领域的拓展，结合新颖的题目情境考查学生的创新能力.要求学生发展迁移的技巧，能用建立的模型来解释新情境，甚至在已建立模型基础上进行延伸，再建构一个新的模型.在日常教学中，我们既要重视基础知识的学习和巩固，也要注重对学生综合能力和面对新情境问题的训练，提升学生的科学思维和科学探究的水平.下面从经典力学、电场、电磁感应、热学、光学、原子物理等知识情境下，讨论“广义”碰撞问题.

2 不同情境下的碰撞

随着新课改的实施，考题多在不同的问题情境下设置，更着重考查学生的科学思维和科学探究的能力，学生解题时需要提取重要信息，联想基础知识，建立模型，最后再选择运用不同工具解决问题.有些题目是在原始物理问题情境中出现，［2］难度会更大些，临场应对能力更加全面.

2.1 经典力学情境

例1.（2020年北京高考真题）在同一竖直平面内，3个完全相同的小钢球（1号、2号、3号）悬挂于同一高度；静止时小球恰能接触且悬线平行，如图1所示.在下列实验中，悬线始终保持绷紧状态，碰撞均为对心正碰.以下分析正确的是

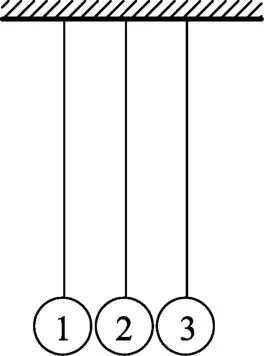
图1

（A）将1号移至高度h释放，碰撞后，观察到2号静止、3号摆至高度h.若2号换成质量不同的小钢球，重复上述实验，3号仍能摆至高度h.

（B）将1、2号一起移至高度h释放，碰撞后，观察到1号静止，2、3号一起摆至高度h，释放后整个过程机械能和动量都守恒.

（C）将右侧涂胶的1号移至高度h释放，1、2号碰撞后粘在一起，根据机械能守恒，3号仍能摆至高度h.

（D）将1号和右侧涂胶的2号一起移至高度h释放，碰撞后，2、3号粘在一起向右运动，未能摆至高度h，释放后整个过程机械能和动量都不守恒.

解析：3个完全相同的小钢球碰撞，结合选项给出的控制条件，提取不同的碰撞模型分析判断.

选项（A）1号球与质量不同的2号球相碰后，1号球的速度不为0，则碰后2号球获得的动能小于1号球刚要碰2号前的动能，所以2号球与3号球相碰后，3号球获得的动能也小于2号球刚要碰3号球前的动能，所以3号球不能摆到h高度，故（A）错误.

选项（B）1、2号球释放后，3小球之间的碰撞为弹性碰撞，且3小球组成的系统只有重力做功，所以系统的机械能守恒，但整个过程中，系统所受合外力不为零，所以系统动量不守恒，故（B）错误.

选项（C）1、2号碰撞后粘在一起，为完全非弹性碰撞，碰撞过程有机械能损失，所以1、2号球再与3号球相碰后，3号球获得的动能不足以使其摆至高度，故（C）错误.

选项（D）碰撞后，2、3号粘在一起，为完全非弹性碰撞，碰撞过程有机械能损失，且整个过程中，系统所受合外力不为0，所以系统的机械能和动量都不守恒，故（D）正确.

点评：题目中虽然没有要求计算，只是个定性判断的问题，但对弹性碰撞、非弹性碰撞和完全非弹性碰撞的区别要比较熟悉.在（A）、（B）选项中，对弹性碰撞的不同情况加以讨论，（A）选项中2号球质量与1号球的质量不同，它所获得的动能要小.（B）、（D）选项中对动量守恒的条件要很清楚，不然容易选错.题目基于牛顿摆实验设计，设置不同的控制条件，突破典型碰撞过程的动量守恒，通过改变小球质量、两个同时摆动、小球涂胶等等进行模型变式，考查学生的模型提取和论证能力.

2.2 电场情境

例2.（2012 年 北 京高考理综真题第24题）匀强电场的方向沿x轴正向，电场强度E随x的分布如图2所示.图中E0和d均为已知量.将带正电的质点A在O点由静止释放.A离开电场足够远后，再将另一带正电的质点B放在O点也由静止释放.当B在电场中运动时，A、B间的相互作用力及相互作用能均为0；B离开电场后，A、B间的相互作用视为静电作用.已知A的电荷量为Q，A和B的质量分别为m和.不计重力.

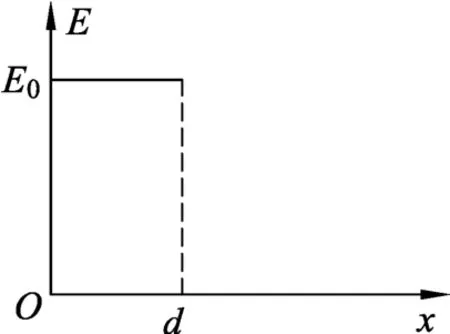
图2

（1）求A在电场中的运动时间t；

（2）若B的电荷量求两质点相互作用能的最大值Epm；

（3）为使B离开电场后不改变运动方向，求B所带电荷量的最大值qm.

解析：（1）A在电场中只受电场力做加速运动，由牛顿第二定律得电场力为恒力，所以A在电场中做匀变速直线运动解得

（2）设A、B离开电场时的速度分别为vA0、vB0，由动能定理得

由（1）式可知vA0＜vB0，B追A，出电场后，只有A、B之间的相互作用力，系统满足动量和能量守恒.A、B相互作用力为斥力，A受的力与其运动方向相同，B受的力与其运动方向相反，相互作用力对A做正功，对B做负功.A、B靠近的过程中，B的路程大于A的路程，由于作用力大小相等，作用力对B做功的绝对值大于对A做功的绝对值，因此相互作用力做功之和为负，相互作用能增加.所以，当A、B最接近时相互作用能最大，此时两者速度相同，设为v′，有

（3）考虑A、B在区间运动，由动量守恒、能量守恒，且在初态和末态均无相互作用，有

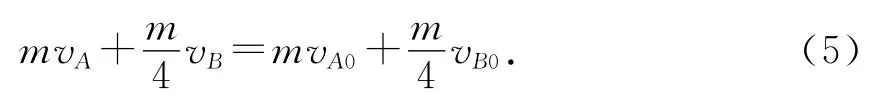
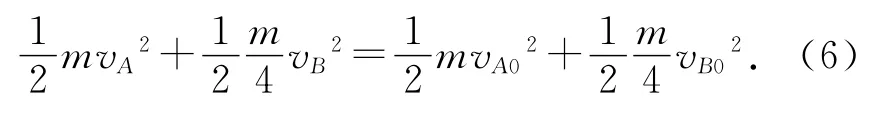
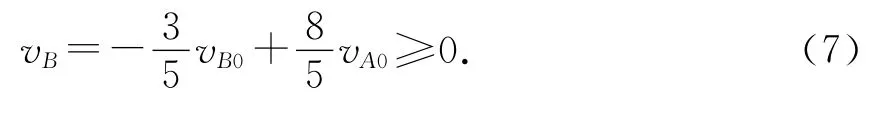
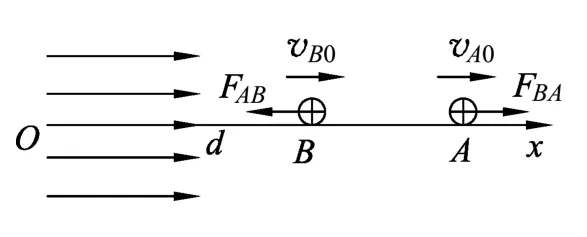
图3

点评：本题第2问要计算出AB两球的初速度，对A和B的初速度进行一个比较，结合弹性碰撞模型情形，画出质点AB出电场后的情景图，有助于基础较弱的学生对问题进行分析.如图3所示，此题情境并不复杂，但增加了电场的知识，需要学生能有比较强的迁移能力，找清楚初始条件，与学过的模型进行联系.依据条件准确画出情景图，是一种化解难度的方法.题目（2）、（3）以点电荷的相互作用为载体，考查相互作用过程的动态分析，二者的相互作用过程符合碰撞模型的典型特征：速度相等时符合完全非弹性碰撞模型、离开无穷远时符合弹性碰撞模型.题目界定了两质点相互作用能，增加了难度要求学生从能量守恒角度，分析得出两质点的动能与相互作用能相互转化，速度相等时相互作用能最大，最大值等于动能的减少量；离开无穷远时两质点的总动能与B刚离开电场时相等，利用弹性碰撞模型，根据B离开电场后运动方向不变的要求，求得B所带电荷量的最大值qm.

应用SPSS 22.0统计软件进行实验数据的统计学分析。所有计量资料均进行正态分布检验和方差分析检验，表格整体数据以均值±标准差（x±s）表示，组间的比较采用单因素方差分析 （One-way ANOVA）并进行方差齐性检验；两两比较采用LSD法；计数资料比较采用χ2检验。P<0.05表示差异有统计学意义。

2.3 电磁感应情境

例3.如图4所示，两条平行光滑导轨相距L，水平导轨足够长，忽略导轨电阻，水平轨道周围有竖直向上的磁感应强度为B的匀强磁场中，金属棒a、b质量分别为m和金属棒b放在水平导轨上，金属棒a从斜轨上高h处自由滑下，设棒a与棒b始终未相撞，金属棒a、b电阻为R、求：金属棒a产生的热量Qa是多少？

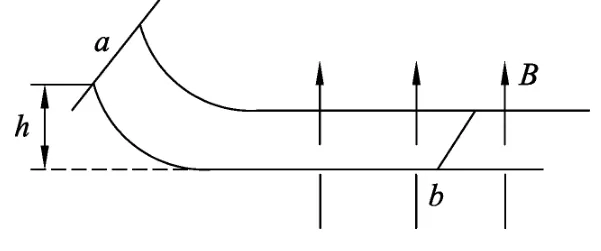
图4

解析：金属棒a从斜轨滑下进入水平轨道后，切割磁感线，回路中产生感应电流，棒a受到水平向左的安培力的作用做减速运动，棒b受水平向右的安培力作用做加速运动.棒a、b切割磁感线使回路产生感应电流，a、b棒发热，随着时间推移，当两棒最终速度相等时，回路中感应电流变为0，棒a、b不受安培力作用，水平方向上没有外力，所以棒a、b以共同速度匀速直线运动.根据能量守恒，求出棒a、b回路产生的总的热量，再根据电阻之间的关系就可以求金属棒a在此过程中产生的热量Qa.设a刚进入水平轨道时速度为v0，则有

之后对棒a、b组成的系统，因为水平方向合力为零，动量守恒，设棒a、b的最终共同速度为v，则有

水平轨道上的整个过程由能量守恒得

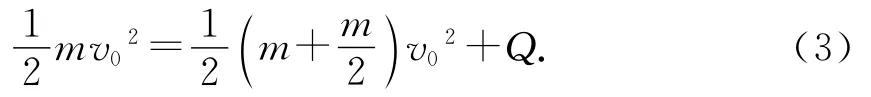
棒ab中电流虽然变化，但发热之比始终不变，可得

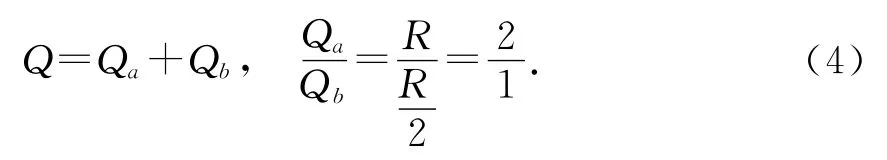
点评：两个金属棒在水平轨道上的运动，受到的安培力等大反向，可以等效成内力.这样，两个金属棒组成的系统动量守恒，最终速度相等，符合完全非弹性碰撞特征.从能量转化角度，系统损失的机械能转化为电能，等于两个金属棒上产生的总电热.电磁感应情境下的“类碰撞过程”需要将两部分的知识结合起来考虑，尤其系统的动量守恒条件和能量转化方向的判定，迷惑性更强.

2.4 热学情境

例4.如图5所示，两端足够长的敞口容器中，有两个可以自由移动的光滑活塞A和B，中间封有一定量的空气，现有一块粘泥C，以动能Ek0沿水平方向飞撞到A并与之粘在一起，由于活塞的压缩，使密封气体的内能增加，设A、B、C质量相等，碰撞时间极短，若不考虑活塞和粘泥所吸收的热量，则密闭空气在碰撞后的绝热变化过程中，内能增加的最大值是多少？

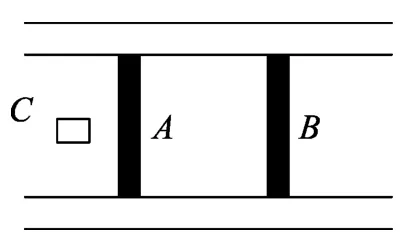
图5

解析：粘泥C飞撞到A并粘在一起的瞬间，可以认为二者组成的系统动量守恒，初速度为v0，末速度为v1，则有mv0=2mv1；在AC一起向右运动的过程中，AB的气体被压缩，压强增大，所以活塞A将减速运动，而活塞B将从静止开始做加速运动，在两活塞的速度相等之前，AB之间的距离减小，气体体积越来越小，内能越来越大，AB速度相等时内能最大，设此时速度为v2，此过程中对ABC组成的系统，由动量守恒定律得（气体质量不计）

由能量的转化和守恒定律可得，在气体压缩过程中系统的动能的减少量等于气体内能的增加量，可得

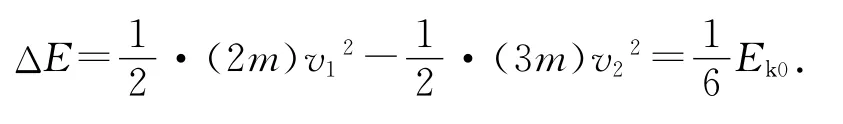
点评：热学的知识学生训练比较少，此情境对很多学生是比较陌生.这种情境能更好地考查学生对碰撞知识的理解.在压缩气体的过程中，CA与B两个活塞受到的内外气体的压力差大小是相等的，方向相反，满足动量守恒的条件，而CA、B活塞所受力做功是不同的，把CA、B的一部分动能转化为气体内能.由热力学第一定律可知：ΔU=Q+W，而密闭气体是绝热过程，增加的内能全部来自做功，把ABC的动能一部分转化为气体的内能.题目涉及两个过程：粘泥C飞撞到A并粘在一起的过程、CA与B相互作用压缩气体直到速度相等的过程.两个过程都符合完全非弹性碰撞模型的特征，都损失了动能，但只有第二个过程中损失的动能才转化为封闭气体的内能.

2.5 光学情境

例5.如图6所示，美国物理学家康普顿及其团队将X射线入射到石墨上，发现被石墨散射的X射线中除了有与入射波长相同的成分外，还有与入射波长不同的成分.我国物理学家吴有训在此项研究中也做出了突出贡献，因此物理学界也把这一效应称为“康普顿 吴效应”.由于这一现象很难用经典电磁理论解释，所以康普顿提出光子不仅有能量，也具有动量，光子的动量p与其对应的波长λ之间的关系为（h为普朗克常量）进一步研究表明X射线的散射实质是单个光子与单个电子发生碰撞的结果.由于电子的速度远小于光的速度，可认为电子在碰撞前是静止的.现探测到散射X射线的波长不同于入射X射线的波长，请你构建一个合理的相互作用模型，解决以下问题：

（1）请定性分析散射后X射线的波长λ′与入射X射线的波长λ的大小关系；

（2）若已知入射X射线的波长为λ，散射后X射线的波长为λ′.设散射X射线相对入射方向的偏转角为θ.求时电子获得的动量.

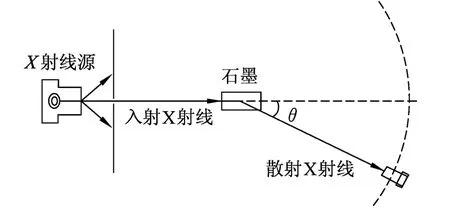
图6

解析：由题意可建构如下模型：X射线中的单个光子与静止的电子发生碰撞，遵守动量守恒定律.

（1）由于入射光子把一部分能量给了电子，则散射后光子的能量减小，光子的频率ν减小，根据可知，光子的波长变大，即λ′＞λ.

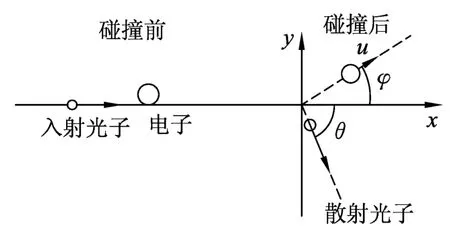
图7

（2）建立图7的坐标系.设电子获得的动量p的方向与入射X射线方向的夹角为φ，动量p在x、y方向上的分量分别为px、py，根据动量守恒定律有，

x方向：

y方向：

其中cosθ=0，sinθ=1，

联立（1）-（4）式可得

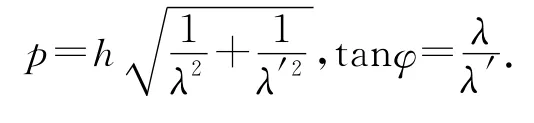
点评：按照光子理论对康普顿效应解释，X射线为一些E=hν的光子，与自由电子发生弹性碰撞，电子获得一部分能量，散射的光子能量减小，频率减小，波长变长.这一过程同时满足动量守恒与能量守恒，其中光子的动量满足本题以康普顿效应的微观过程为载体，对光子碰撞电子的过程进行分析，把碰撞模型从一维拓展到二维，给出了光子的动量表达式，提示建立二维坐标系把矢量运算化为代数运算的方法，分别在两个方向上把碰撞后的动量进行矢量分解，然后分别根据动量守恒列式.把弹性碰撞动碰静的模型进行了适度的拓展，碰撞前后运动不在一条直线上，需要对碰撞后动量矢量分解，而且动量的表达式不是质量与速度的乘积.

2.6 原子物理情境

例6.中子的发现是物理史上的一件大事.1930年科学家在真空条件下用α射线轰击铍核94Be时，发现一种看不见、贯穿能力极强的不知名射线和另一种粒子产生.这种不知名射线具有如下特点：（1）在任意方向的磁场中均不发生偏转；（2）这种射线的速度远小于光速；（3）用它轰击含有氢核的物质，可以把氢核打出来；用它轰击含有氮核的物质，可以把氮核打出来.实验中测得，被打出氢核的最大速度为3.3×107m/s，氮核的最大速度为4.7×106m/s，假定该射线中的粒子均具有相同的能量，氢核和氮核碰前可认为是静止的，碰撞过程中没有动能的损失.已知氢核质量MH与氮核质量MN之比为1∶14.根据以上信息，不考虑相对论效应，完成下列问题.求：请通过计算判断该射线中的粒子是否为卢瑟福所预言的中子，并通过分析说明依据.

解析：设组成该射线的粒子质量为m，轰击含有氢核或氮核的物质时速度为v.由于碰撞过程中没有动能损失，当被打出的氢核和氮核的速度为最大值时，表明其碰撞为弹性碰撞.设与氢核发生弹性正碰后粒子速度为v1，氢核速度为vH；与氮核发生弹性正碰后粒子速度为v2，氮核速度为vN.根据动量守恒和机械能守恒，轰击氢核

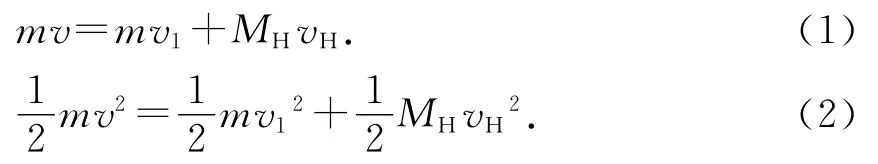
解得

轰击氮核

解得

由（3）、（6）式解得m=1.16MH≈MH.计算得该射线粒子的质量与质子（氢核）的质量近似相等，磁场中不偏转说明不带电荷，表明这种射线粒子就是卢瑟福所预言的中子.

点评：动量守恒定律既适用于宏观，也适用于微观，原子物理问题中的碰撞，与传统力学的碰撞非常相似，只要找清楚碰撞对象和数量关系，就容易解决问题.宏观情境下的问题和微观情境下的问题有很多相似之处，只是观察的尺寸不同，在微观粒子的相互作用过程中，运用经典力学的观点，类比弹性碰撞或非弹性碰撞模型分析研究，是一种常用的处理方法，这种方法在高中阶段用得更多.

3 结论

碰撞模型是高中物理中一个重要的理想化过程模型，在应用模型解决问题的过程中，从研究对象看，碰撞模型中都会牵扯到两个及以上物体；从物理观念看，碰撞模型涉及相互作用观、运动观、能量观；从解决问题的思维过程来看，需要学生进行模型建构、科学推理、分析判断、数学运算等；从科学探究来看，每一次解决不同的情境下的碰撞问题，都会有新知探索和旧知的联系.在面对一个新的问题时，除需要进行常规分析，画出合理的情境图，分析系统的受力情况，判断是否满足动量守恒外，判定题目涉及的相互作用过程是否符合碰撞模型特征，并结合题目的限制条件区分属于哪一种碰撞，借助碰撞模型分析系统能量的转化或转移的方向，进而列出相应的方程，运用一定的数学计算技巧，才能解决类似的问题.通过解决不同情境下的“等效碰撞”问题，锻炼学生的模型拓展和模型应用能力.