汽油辛烷值损失模型建立与分析叶

怡豪 仲梁维

摘  要：针对汽油催化裂化过程中减少辛烷值损失值的问题，基于某企业催化裂化汽油精制脱硫设备的样本数据库数据，通过数据挖掘技术建立汽油精制过程中的辛烷值（RON）模型。首先，对初始数据进行规范化，然后运用随机森林法对数据变量进行降维，提取出因变量贡献程度较大的30 个主要变量;其次，利用BP神经网络，建立辛烷值损失模型;最后，在建立的模型中确定初始样本，结合遗传算法对操作变量进行优化。结果表明：优化后的辛烷值损失值下降的幅度为42.14%，降幅大于30%，有助于在实际生产中减少辛烷值损失，降低企业经济损失。

关键词：随机森林法;汽油辛烷值;BP神经网络模型;遗传算法

中图分类号：TP183     文献标识码：A

Abstract： Aiming at the problem of reducing octane number loss in the process of gasoline catalytic cracking， this paper proposes to establish a research octane number （RON） model in the gasoline refining process through data mining technology， based on the sample database data of a company's catalytic cracking gasoline refinement and desulfurization equipment. Firstly， initial data is normalized. Then， random forest method is used to reduce the dimensionality of the data variables， and the 30 main variables that contribute to the dependent variable are extracted. Secondly， BP neural network is used to establish the RON loss model. Finally， the initial sample is determined in the model， and the operating variables are optimized in combination with genetic algorithm. Results show that the optimized RON loss value decreases by 42.14%， which is more than 30%. The proposed model helps to reduce the octane loss in actual production， so to reduce the economic losses of enterprises.

Keywords： random forest method; gasoline octane number; BP neural network model; genetic algorithm

1   引言（Introduction）

隨着计算机的发展，数据分析、算法在科学技术领域中的应用越来越广泛[1]。汽油作为当前主要燃料之一，在实际生产的催化裂化过程中是通过降低汽油辛烷值的手段来进行脱硫、脱烯烃的，虽然能达到降低硫、烯烃含量的目的，但是辛烷值作为汽油抗震抗爆的主要指标，辛烷值的降低将带来较大的经济损失[2]。在生产环节中，需要建立辛烷值损失模型对影响因素进行分析和优化，达到减少辛烷值损失的目的[3]。本文通过数据挖掘技术结合随机森林法对数据样本进行剔除和筛选，建立基于BP神经网络的辛烷值损失模型，该模型对降低辛烷值损失值有明显优化，为汽油催化裂化过程中提高辛烷值数值提供解决方法。

2   样本数据处理（Sample data processing）

2.1   数据预处理

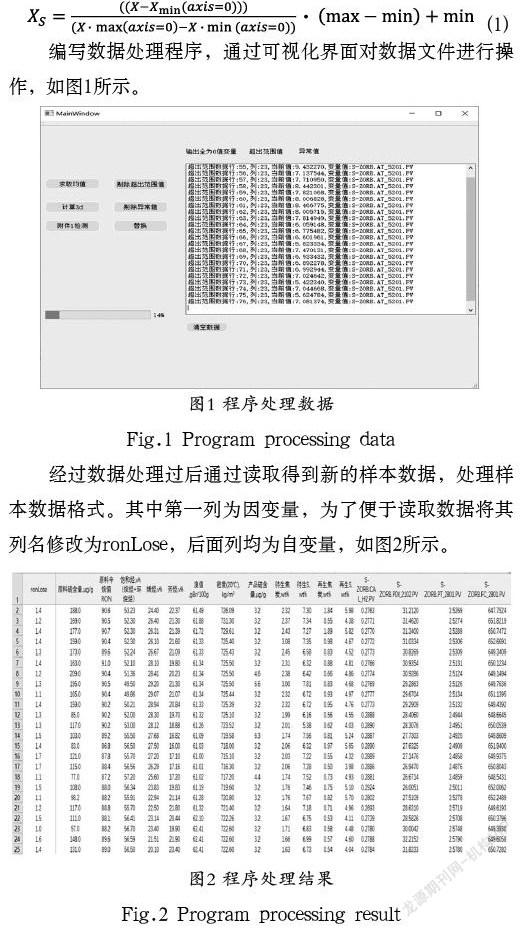
数据来源为某企业催化裂化汽油精制脱硫设备的样本数据库数据，数据包括原料性质、待生吸附剂性质、再生吸附剂性质等操作变量，共计367 个变量。将数据文件命名为附件1，对初始数据进行处理，删除样本中数据全部为空值的位点。对于只含有部分时间点的位点，如果其残缺数据较多，无法补充，将此类位点删除。根据工艺要求与操作经验，总结出原始数据变量的操作范围，然后采用最大最小的限幅方法剔除一部分不在此范围的样本[4]。根据拉依达准则法寻找操作变量中异常值，将其数值设置为0。根据数据分析中的二八法则，如果操作变量中0值和缺省值样本数所占总样本数的比例超过20%，那么将该操作因子直接去除;如果小于20%，统计计算除了0值以外的其他数的平均值，再替换原来的0值。对特征进行方差计算，剔除方差值特别小的因子。为了统一判断，需要先将数据归一化处理，归一化到[0，1]，然后计算某一列的方差，若某一个特征中的数据基本一致，认为该特征包含的可用信息比较少，方差阈值s2定为0.01，如果方差小于0.01，将该特征剔除。归一化公式如公式（1）所示。

经过数据处理过后通过读取得到新的样本数据，处理样本数据格式。其中第一列为因变量，为了便于读取数据将其列名修改为ronLose，后面列均为自变量，如图2所示。

2.2   模型主要变量

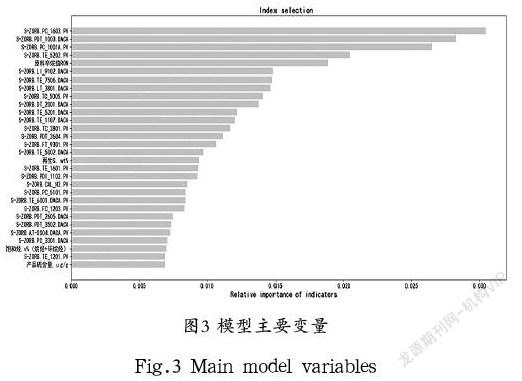
选取辛烷值损失值作为因变量，分析样本数据可知，若将所有操作变量输入，可能会导致过拟合，影响结果，且操作变量的关系存在高度耦合，呈现非线性关系，传统的降维方法是不合适的。采用随机森林法作为特征的筛选算法，将特征基于因变量贡献程度进行排序，选择靠前的30 个特征作为主要变量，进行降维得出的30 个主要变量[5]如图3所示。

3    辛烷值损失预测模型（RON loss prediction model）

3.1   模型选择

考虑到辛烷值损失受到多种操作变量的影响，呈现难以解析的非线性关系，BP神经网络算法具有解决多重因素交叉影响的复杂非线性问题的能力，有效处理多层网络模型中隐含层的连接权问题，大幅优化神经网络的组织和自学习能力，因此采用BP神经网络算法对辛烷值损失建立预测模型[6-7]。

BP神经网络是多层的前馈神经网络，其主要的特征是信号是前向传播的，而误差是反向传播的。它模拟了人脑的神经网络结构，人脑传递信息的基本单位是神经元，人脑中有大量的神经元，每个神经元与多个神经元相连接。每层神经网络都是由神经元构成的，单独的每个神经元相当于一个感知器。输入层是单层结构的，输出层也是单层结构的，而隐藏层可以有多层，也可以是单层的。输入层、隐藏层、输出层之间的神经元都是相互连接的。总的来说，BP神经网络结构流程是输入层得到信息后会把信息传给隐藏层，隐藏层则会根据神经元相互联系的权重并根据规则把这个信息传给输出层，输出层对比结果，如果不在预计范围内，则返回调整神经元相互联系的权值，不断进行训练，直至到达预期结果[8]。BP神经网络模型算法流程图如图4所示。

3.2   模型建立

建立辛烷值损失的BP神经网络模型，模型建立过程如下所示：

（1）选取训练样本以及测试样本。样本是依据时间测定的，为了避免随机选取过程中可能存在某个时间段样本较多的情况，且并不确定样本数据可能与时间序列有某种关联，故通过均匀方式选取样本。数据文件中样本按序号排列，能被4整除的样本序号定为测试样本，反之为训练样本。最终获得244 个训练样本，81 个测试样本。

（2）对数值进行归一化。由于输入数据的单位不一样，有些数据的范围可能特别大，导致的结果是神经网络收敛慢、训练时间长。数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用就可能会偏小。由于神经网络输出层的激活函数的值域是有限制的，因此需要将网络训练的目标数据映射到激活函数的值域。例如，神经网络的输出层若采用双曲正切S形激活函数，由于双曲正切S形函数的值域限制在（-1，1），也就是说神经网络的输出只能限制在（-1，1），因此训练数据的输出就要归一化到[-1，1]区间。

当激活函数采用双极S形函数进行归一化处理时，如公式（2）所示，其中min为矩阵中最小值，max为最大值。

（3）使用函数创建神经网络。该函数需要几个重要参数，包括隐含层层数、隐含层神经元数量、输出层神经元个数以及激活函数和训练算法。其中输入层由隐含层作用于输出层，通过非线性变换获取输出量，训练中的每个数据都拥有输入值和期望输出值，网络输出值与期望输出值两者的偏差经过修改阈值和网络权值，使误差沿梯度方向下降，最终使期望输出和实际输出在预定范围中[9]。

设输出层有m 个神经元，BP神经网络的实际输出是y，期望输出是y'，函数如公式（3）所示。

式中，为输入单元i到隐含层单元j的权重，是学习效率，是中间第j 个隐含层的传输函数。使用提取到的30 个建模主要变量（辛烷值除外）作为神经网络模型的输入参数，确定输入端点数为30。该BP神经网络模型采用三层网络，结构为30-n-1，其网络结构图如图5所示。

在其他条件完全相同的情况下，只改变隐含层神经元数量，每次固定隐含层神经元数量后，获取四次预测结果，取平均值作为该组数据的最终结果。

对于激活函数的选取，由于操作变量（控制变量）之间具有高度非线性，此外，样本数据归一化处理后的值域为[-1，1]，故激活函数选取双曲正切S形函数，如公式（5）所示。

模型最终要预测出辛烷值损失这一个量，故输出层神经元个数为1，训练算法选取最小二乘法，其收敛速度较快，并能使所求数据与实际数据之间误差的平方和为最小。

（4）BP神经网络参数设置，如表1所示。

（5）模型训练完成后，输入测试样本，获取预测值，计算绝对误差，并绘制误差频率直方图、误差变化图。

3.3   模型分析

在其他条件完全相同的情况下，只改变隐含层神经元数量，每次固定隐含层神经元数量后，获取四次预测结果，取平均值作为该组数据的最终结果，如表2所示。

从表2中的分析可知，当隐含层神经元个数为10时，81 个预测样本的预测辛烷值损失与实际值的均方误差误差最小，故隐含层神经元个数取10。

选定隐含层神经元个数后，求解辛烷值损失预测模型，如图6—图10所示。

4   样本变量优化（Sample variable optimization）

4.1   样本选择

根据BP神经网络建立的辛烷值损失预测模型，筛选数据作为优化样本，从筛选出的样本中保持原料、待生吸附剂、再生吸附剂的性质不变。对于其他筛选出来的主要变量，在各自变量的范围内随机产生数据，产生的数据利用遗传算法结合建立的预测模型进行寻优，进行该样本的操作变量方案的优化。

选取某一个样本进行分析和优化，其他样本的分析和优化完全一致。样本选择确定原则：S的含量要低于5 μg/g;选择众数值为3.2的样品;原料中的辛烷值不能过低，选择平均数89.7;辛烷值初始损失值不能过低，否则没有优化的意义，这里选择众数值为1.4。结合这几点最终挑选样本号为264的样本作为分析对象来研究操作变量的优化。

4.2   优化模型建立与分析

初始样本确定后，结合操作变量和操作变量的取值区间，随机产生1，000 个随机数据作为初始种群，将建立的BP神经网络作为适应度函数表示，优化目标为最小化辛烷值损失值。初始种群进行交叉、遗传、变异、选择操作，设置迭代次数为100 次，筛选出最优的个体作为优化值[10]。但是由于初始种群的问题可能会导致无法求解到最优值，可能陷入局部最优的状态，因此逐步增大初始种群的大小进行反复验算[11]。我们发现随着初始种群规模的增大，辛烷值损失值的变化刚开始存在波動，但是当初始种群大于8万个左右时，辛烷值的损失值逐步下降最后趋于稳定状态，最终得到最优的操作变化的优化条件和辛烷值损失值。

随着随机样本数量的增加，刚开始辛烷值的损失值会存在波动，但是当初始样本数量大于80，000左右的时候，辛烷值的损失值逐步稳定，接近0.81。辛烷值的损失值随着初始样本数量变化的关系趋势如图11所示。

最终经过优化，优化后的辛烷值损失值为0.81，相较于原来数据样本中的初始值1.4，下降的幅度为42.14%，降幅大于30%，说明操作变量起到优化的作用。优化后的操作变量的取值如表3所示。

5   结论（Conclusion）

基于建立的辛烷值损失模型，结合遗传算法对操作变量进行改变，得到优化后的辛烷值损失值为0.81，相较于原来数据样本中的初始值1.4，下降的幅度为42.14%，利用该模型对降低辛烷值损失值起到优化效果。

参考文献（References）

[1] 王浩滢.深度学习及其发展趋势研究综述[J].电子制作，       2021（10）：92-95.

[2] 胥红玉.浅谈汽油辛烷值的影响因素[J].品牌与标准化，      2020（05）：49-50，52.

[3] ZHU J J， LAN B. Research on model of octane number loss based on XgBoost[J]. International Core Journal of Engineering， 2021，7（1）：496-501.

[4] 杨斌，田永青，朱仲英.智能建模方法中的数据预处理[J].信息与控制，2002（04）：380-384.

[5] 杨森彬.线性回归和随机森林算法融合在餐饮客流量的预测[J].软件工程，2018，21（07）：24-27.

[6] 张宏，马岩，李勇，等.基于遗传BP神经网络的核桃破裂功预测模型[J].农业工程学报，2014，30（18）：78-84.

[7] 钟健，阎春平，曹卫东，等.基于BP神经网络和FPA的高速干    切滚齿工艺参数低碳优化决策[J].工程设计学报，2017，     24（04）：449-458.

[8] 张喆，张永林，陈书锦.基于遗传BP神经网络的搅拌摩擦焊温度模型[J].热加工工艺，2020，49（03）：142-145.

[9] 薛风华，徐微微，王洪寅，等.基于神经网络的并网光伏电站自适应距离保护[J].电工电气，2020（04）：25-29.

[10] 张晓丽，肖满生，叶紫璇.基于遗传算法的图像多特征权重自动赋值方法[J].软件工程，2019，22（10）：22-26.

[11] 徐寿臣，王春玲，赵泽昆，等.基于GA-BP神经网络的电池储能系统软故障模糊综合评价[J].电器与能效管理技术，2017（13）：74-81.

作者简介：

叶怡豪（1998-），男，硕士生.研究领域：计算机辅助设计与智能开发.

仲梁维（1962-），男，碩士，教授.研究领域：计算机辅助设计，企业信息化.