一种同轴双向回转模式的钻具结构设计及振动模拟

曹彦伟，李谦

（成都理工大学环境与土木工程学院，四川 成都 610051）

0 引言

钻进过程中，因为同时受到轴向压力、扭矩和弯曲力矩的作用，井下钻柱振动不可避免。更为严重的是钻柱自转时还存在着剧烈的交变应力，会使钻柱受到的扭矩大大增加，导致其下部受力最大［1］。减少钻柱振动是钻进过程优化的关键问题之一，近年来对该问题的研究集中于被动减振和主动减振2种方式。被动减振的原理是在振动产生后降低振动幅度，通过使用优化设计的钻柱组合或者是在钻柱的下端安装抑制振动的工具实现减振。主动减振的原理在于对钻头进行结构化设计，在源头上抑制振动的产生。当前常用的减振手段大多为侧重于使用减振工具降低振动的被动减振，刘希茂等研制的随钻恒扭器可以稳定钻井扭矩，提高钻头使用寿命［2］；查春青等设计了PDC钻头扭转振动减振工具能够有效抑制钻头的扭转振动［3］；付传红等研制的减振增压装置可以实现稳定给钻头增压的同时极大限度地吸收钻柱振动和钻头冲击［4］；付蒙等基于速度补偿反馈控制器设计出的钻柱粘滑振动控制系统可以有效抑制钻柱粘滑振动［5］。Shell和NOV公司合作开发的软扭矩旋转系统，通过自适应控制顶驱转速来消除粘滑振动［6］；Tomax公司开发出能够适时调整钻进扭矩的井下工具，可以实现扭矩自平衡［7］。就主动减振而言，有学者对全尺寸试验井中振动参数进行了实测，指出当前常用的5种减振钻头设计理论都不能有效地实现减振［8］。

为探索主动减振的可行性，本文设计出一种基于行星齿轮系驱动双层钻杆带动内外钻头进行同轴双向回转运动的钻具结构，以期降低钻进过程中钻头与地层摩擦产生的反作用力，借此减少钻柱振动以实现主动减振。本文主要对该结构的核心部件进行了强度校核分析，同时对减振效果也进行了数值模拟。

1 实现双向回转钻进运动的钻具结构设计

1.1 基础结构设计分析

如图1所示，该钻具结构核心在于如图1（c）所示的行星齿轮系，分别由安装在内钻杆3上的太阳齿轮20、行星齿轮19和安装在外钻杆6上的外齿圈21构成。行星齿轮19被安装在行星齿轮架7上，行星齿轮架7通过固定外壳连接件5与固定外壳2连接在一起。如图1（a），固定外壳2外形类似于稳定器，由含硬质合金颗粒的高耐磨性胎体制作，最大尺寸略大于外钻杆6的外径。如此设计可保证在钻探过程中固定外壳2可以依靠与钻孔壁之间的摩擦力保持不转，从而使齿轮架7保持不动，使得工作时的行星齿轮19与太阳齿轮20啮合只自转不公转。当动力从带有太阳齿轮20的内钻杆3输入时，太阳齿轮20带动与之啮合的行星齿轮19转动，行星齿轮19被齿轮架7限制只自转，从而带动固定有外齿圈21的外钻杆6产生与内钻杆3相反的旋转运动，实现双向回转。

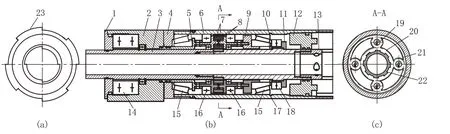
图1 双向回转钻具结构设计示意Fig.1 Design of the coaxial contra⁃rotary drill structure

内钻杆和外钻杆下端留有接头可以安装不同尺寸的钻头。钻进过程中内外钻头产生相反的扭矩和振动，使扭矩和振动相互平衡，内钻头与内钻杆之间留有水口，保证钻井液能充分流入内外钻头之间的间隙，为便于安装，将双向回转钻具结构的内钻杆分成2部分，分开的2段通过螺纹连接在一起，在断开的位置用矩形花键周向固定中心齿轮。

1.2 行星齿轮系设计

1.2.1 整体结构的均载与发热

在理想的制造精度下，能够达到中心轮向各个行星齿轮的啮合力大小相同，但是现实的加工条件无法达到理想的制造精度和安装精度，可以通过在行星齿轮系中添加“均载机构”的方式使行星齿轮传动过程中构件与构件之间达到自动补偿误差的效果［9］；实现双向回转运动的钻具结构核心行星齿轮系采用水平放置的渐开线圆柱直齿轮传动，垂直放置的齿轮系会受到重力的作用而导致载荷不均，所以相比于垂直放置的齿轮系，水平放置的齿轮系载荷分布更均匀。校核计算时大齿轮与小齿轮之间传递的圆周力平均分配，即4个行星齿轮受到的圆周力等于中心齿轮和外齿圈受到的圆周力。双向回转钻具结构钻进时行星齿轮只自转，故齿轮校核可按定轴轮系校核计算。

当齿轮转速较高且所受扭矩较大时，齿轮间压力大、瞬间温度高会造成齿轮胶合的现象，影响齿轮传动。文献［10］通过试验找出了齿轮的热胶合发生的失效边界，齿轮材料为18CrNiMo7-6，当齿轮转速固定为2500 r/min、齿轮转矩达到2500 N·m时齿面最大接触温度达到220℃，发生胶合；当齿轮转矩固定为2000 N·m、齿轮转速达到4000 r/min时齿面最大接触温度达到217℃，发生胶合；根据《地质岩心钻探规程》（DZ/T 0227—2010）［11］，金刚石孕镶钻头最大适用转速为1500 r/min，可以看出正常钻探的转速和齿轮发生胶合时的转速相差较大，不容易发生胶合。

1.2.2 行星齿轮扭矩估算

由于设计初始齿轮的尺寸和参数未知，故设计时需先初步选定所需参数，然后进行精确校核计算，并根据校核计算的结果对参数重新调整。根据圆柱齿轮齿面接触强度公式［12］，初步估算行星齿轮的扭矩T1，如式（1）所示：

式中：d1——行星齿轮分度圆直径，mm；K——载荷系数，一般取1.2~2，直齿轮取较大值，取1.7；T1——小齿轮即行星齿轮所受扭矩，N·m；Фd——齿宽系数，当齿面硬度小于350 HBW齿轮对称布置并靠近轴承时，Фd=0.8~1.4，齿面硬度>350 HBW，Фd数值应降低50%。齿轮材料选择材料强度较高的渗碳钢，型号为20CrMnMn，该材料齿面硬度大于350 HBW，因此取0.7；σHP——许用接触应力，N/mm2，简化计算中近似取σHP≈σHlim/SHmin，σHlim为齿轮的接触疲劳极限应力，根据机械设计手册［12］查齿面接触疲劳极限图得1500 N/mm2，SHmin为接触强度计算的最小安全系数，SHmin≥1.1，取SHmin=1.1；u——齿轮传动比。

总体初步设计结构外径125 mm，内钻杆内径为38 mm。由于外齿圈位于齿轮系的最外部，外径125 mm，外钻杆壁厚定为7.5 mm，外齿圈分度圆直径必须小于外钻杆的内径，故确定外齿圈分度圆直径为100 mm。设定内钻杆外径为55 mm，固定在内钻杆上的太阳齿轮分度圆直径要稍大于结构内钻杆的外径，故确定太阳齿轮的分度圆直径为60 mm。由太阳齿轮和外齿圈分度圆直径得出行星齿轮分度圆直径为20 mm，行星齿轮对太阳齿轮的传动比为3。齿轮材料采用20CrMnMn渗碳钢，接触疲劳极限应力σHlim=1500 MPa，弯曲疲劳极限应力σFlim=460 MPa。计算可得行星齿轮扭矩T1≤10.2 N·m，取T1=10.1 N·m。

1.2.3 行星齿轮模数估算

根据齿面弯曲强度公式初步估算行星齿轮模数m如式（2）所示，假定小齿轮齿数z1=20，则计算得齿轮模数m≥0.95，取m=1。

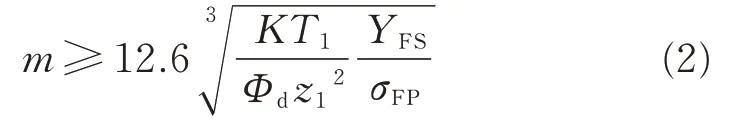
式中：σFP——许用弯曲应力，N/mm3，简化计算中近似取σFP≈σFE/SFmin，σFE为齿轮材料弯曲疲劳强度基本值，根据齿轮的材料和机械设计手册查齿根弯曲疲劳极限图得920 N/mm2，SFmin为抗弯强度计算的最小安全系数，SFmin≥1.4，取SFmin=1.4；YFS——复合齿形系数，根据齿轮齿数查外齿轮的复合齿形系数表得4.55；z1——小齿轮即行星齿轮齿数。m——齿轮模数，mm。

1.2.4 齿面接触疲劳强度校核

根据《渐开线圆柱齿轮承载能力计算方法》（GB/T 3480—1997），齿面接触疲劳强度计算应力σH如式（3）所示，其中行星齿轮与太阳齿轮的齿面接触疲劳强度取正，行星齿轮与外齿圈的齿面接触疲劳强度取负。

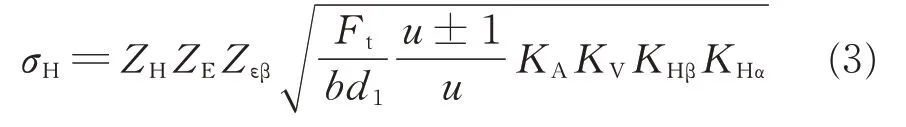
式中：Ft——分度圆上的圆周力，N；b——齿宽，mm；KA——使用系数，原动机为步进电动机，载荷均匀平稳，工作机为钻具结构，载荷为强烈振动，根据机械设计手册［12］查使用系数表得KA=1.75；KV——动载系数，查动载系数图得KV=1.04；KHβ——接触强度计算的齿向载荷分布系数，查硬齿面齿轮KHβ表得KHβ=1.22；KHα——接触强度计算的齿向载荷分布系数，查齿间载荷分配系数表得行星齿轮与太阳齿轮KHα=1.29，行星齿轮与外齿圈KHα=1.93；ZH——节点区域系数，根据查节点区域系数表得ZH=2.5；ZE——弹性系数，查弹性系数表得ZE=189.8；Zεβ——重合度与螺旋角系数，直齿轮Zεβ=Zε，根据重合度系数公式算出行星齿轮与太阳齿轮为0.88，行星齿轮与外齿圈为0.72。

代入相关数值进行计算，得到计算应力σH=1549.8 MPa，安全系数取SHlim=1.25，而许用应力计算值σHP=1103.7 MPa，σH>σHP，不满足条件，根据齿面接触强度许用应力值算出齿轮分度圆上最大圆周力Ft，再根据行星齿轮分度圆直径与圆周力Ft得出T1=5.1 N·m；代回式（3）重新校核接触疲劳强度，得到计算应力σH=1101.3 MPa，σH≤σHP，行星齿轮与太阳齿轮的齿面接触疲劳强度满足要求。由于外齿圈是内齿轮，使用公式（3）中减号进行校核，得到σH计算应力=779.3 MPa，σH<σHP，故同时满足要求。

1.2.5 齿根弯曲疲劳强度校核

根据《渐开线圆柱齿轮承载能力计算方法》（GB/T 3480—1997），齿根弯曲疲劳强度计算应力σF如式（4）所示。

式中：KFβ——弯曲强度计算的齿向载荷分布系数，简化计算中KFβ=KHβ=1.22；KFα——弯曲强度计算的齿间载荷分布系数，根据机械设计手册查齿间载荷分配系数表得行星齿轮与太阳齿轮的KFα1=1.43，行星齿轮与外齿圈齿间载荷系数的KFα2=1.54；YFS——复合齿形系数，根据齿轮齿数查复合齿形系数表得行星齿轮YFS1=4.55，太阳齿轮YFS2=3.95，外齿圈YFS3=5.44；Yεβ——抗弯强度计算的重合度系数与螺旋角系数，直齿轮Yεβ=Yε，根据机械设计手册查图得行星齿轮与太阳齿轮的Yε1=0.7，行星齿轮与外齿圈的Yε2=0.65。

代入相关参数计算，得到行星齿轮与太阳齿轮计算应力σF1=368.4 MPa，行星齿轮与外齿圈计算应力σF2=440.5 MPa，安全系数取SHlim=1.6，许用应力计算 值为σFP=540.5 MPa，两 组计算应 力σF1、σF2均小于许用应力σFP，满足要求。

1.2.6 确定齿轮几何参数

经上述参数计算，最终确定满足强度的齿轮几何参数如表1所示。

1.3 密封设计

为防止钻进过程中钻井液流体渗入损坏内部轴承和齿轮，结构必须进行密封设计与校核。双向回转钻具结构拟采用O形密封圈作为密封件，对内外钻杆的环空间隙进行密封。当O形圈用于旋转密封时，为避免与运动的旋转轴的接触处产生摩擦热使橡胶材料受热严重变形加速密封材料老化，降低使用寿命，故采用氟橡胶作为O形圈材料［12］，密封压力最大可达35 MPa。

为验证结构密封性，采用计算机模拟钻井液流入双向回转钻具结构并流出的过程［13］，测出结构密封位置的压强，以模拟结果与O形密封圈的最大密封压力对比进行密封效果校核。122 mm公称口径钻头选择泵量为100 L/min，钻井液密度选取1.25 g/cm3。井深取2400 m，根据井深与钻井液密度得出钻井液静止压力为26.3 MPa，设置双向回转钻具结构内钻杆上端为进口，入口控制类型设置为流速控制，钻井液入口速度恒定不变，进口流速由泥浆泵量换算得1.21 m/s。外钻杆与钻井壁之间的间隙为出口，出口控制类型设置为平均压力，压力值为26.3 MPa，壁面条件采用无滑移。数值模拟结果如图2所示。图中内外流道之间的间隙就是结构密封的位置，该处的压强为26.303 MPa，取安全系数为1.25，得到考虑安全系数的压强为32.88 MPa。O形密封圈最大密封压力为35 MPa，密封处压强为32.88 MPa≤35 MPa，故密封系统能够满足正常工作的需要。

1.4 轴承设计

双向回转钻具结构的内外钻杆存在相对旋转，且需承受来自钻柱的轴向压力，所以双向回转钻具结构的内外钻杆之间必须要设置轴承，用于支撑分离内外环相对运动的钻杆。故如图3所示，为防止外钻杆受力后向上移动，在双向回转结构下端设置圆锥滚子轴承6并在外钻杆设置挡圈，固定住轴承，在固定外壳处设置推力球轴承1限制外钻杆向上移动；为支撑双向回转结构内外钻杆之间的机构，使用推力圆柱滚子轴承支撑住圆锥滚子轴承的内环，防止内部结构下落；在行星齿轮架的上下设置深沟球轴承4提高结构周向的稳定性；在外钻杆与固定外壳连接件之间设置圆锥滚子轴承3加强结构周向的稳定性；为降低行星齿轮架与行星齿轮之间的摩擦，在两者之间设置深沟球轴承5降低转动摩擦；为提高固定外壳与内钻杆之间的周向稳定性，设置深沟球轴承2加强结构周向的稳定性。

钻具在井下钻进过程中主要承受轴向的钻压，所以只对承受轴向压力的圆锥滚子轴承6和推力球轴承1进行校核。正常工作条件下Ø122 mm钻头工作负载为12~17 kN，取钻头负载为12 kN校核。孕镶钻头底唇面的线速度范围为1.5~3 m/s，结合双向回转钻具结构内钻杆直径得出该尺寸下金刚石钻进最大转速为519~1038 r/min；双向回转钻具结构中推力圆柱滚子轴承极限转速最低，轴承极限转速为1200 r/min≥519~1038 r/min，故轴承转速满足要求。由于深沟球轴承只承受径向荷载，推力圆柱滚子轴承只用于降低固定件与圆锥滚子轴承之间的摩擦，不承受轴向压力。故只需校核单列圆锥滚子轴承与双向推力球轴承，轴承校核计算公式如式（5）所示：

式中：fh——寿命因数，额定寿命取240 h，根据文献［14］知球轴承为0.783，滚子轴承为0.802；fn——速度因数，额定转速取1000 r/min，查速度因数表得fn=0.36；fm——力矩载荷因数，转矩载荷较小，取fm=1.5；fd——冲击载荷因数，强大冲击，取1.8；fT——温度因数，取地面常温20℃（fT=1）和2000 m井深地温120℃（fT=0.95）分别校核，2000 m井深地温按5℃/100 m计算得到；P——当量动荷载，kN；X、Y——分别为径向、轴向动荷载系数，查表得圆锥滚子轴承X=0.4，Y=1.6，推力球轴承X=0，Y=1；Fr、Fa——分别为径向、轴向荷载，kN。

取地面常温20℃进行校核，单列圆锥滚子轴承计算基本额定动荷载计算值115.5 kN<额定荷载142 kN。双向推力球轴承基本额定动荷载计算值70.5 kN<额定荷载74.8 kN，满足要求；取2000 m井深处地温120℃进行校核，得到单列圆锥滚子轴承基本额定动荷载计算值121.6 kN<额定荷载142 kN。双向推力球轴承基本额定动荷载计算值74.2 kN<额定荷载74.8 kN，满足要求。故经计算在钻头工作负载为12 kN时轴承能满足正常工作需要。轴承选用参数如表2所示。

2 双向回转钻具结构的振动模拟

2.1 双向回转钻具结构的模态分析

为确定双向回转钻具结构的振动特性及其与普通单向回转钻进结构振动特性的差异性，分别建立双向回转钻具结构和普通单向回转钻进结构的三维模型进行振动模态分析。模型相关参数如下。

（1）模型尺寸：普通单向回转钻进结构模型高度与双向回转钻具结构模型高度相同，与钻头连接的钻杆壁厚为11 mm，钻杆外壁直径同样为125 mm，保持模型外形尺寸相同。

（2）模型建立：由于双向回转钻具三维模型零件较多、特征较复杂，在力学性能与原结构保持一致的前提下，模态分析时对双向回转模型进行一定的简化，简化方案为：倒角圆角尽可能简化为直角；轴承简化为空心圆柱体；不影响计算的基础尽可能简化或忽略螺纹、凹槽等结构特征［14］。

（3）材料设置：为简便计算两种钻进结构的材料属性考虑均采用结构钢：密度ρ=7850 kg/m3，弹性模量E=200 GPa，泊松比μ=0.3。

（4）网格划分：由于齿轮的尺寸相对整个双向回转结构的尺寸较小，为使计算结果更加准确，网格划分时控制齿轮及一些尺寸较小零件的网格尺寸2 mm，其他零件网格大小按照7 mm自动划分网格，最终得有限元模型单元数为130130，节点数为323091。

（5）接触关系：装配体中两零件之间若不会移动，设置为绑定接触；如果两个零件之间有相对移动，比如轴承与壳体之间的接触，设置为摩擦接触，尽可能模拟接近真实的接触情况。

（6）边界条件：固定外壳可通过与地层间的摩擦力保持不转，因此约束双向回转钻具结构固定外壳4个刀刃的旋转自由度，以及固定双向回转钻具结构内钻杆上端；普通单向回转钻进结构钻杆上端固定［15］。

各阶模态振型如图4所示。（1）2种结构第一、二阶的模态振型都是横向摆动，变形从上至下都逐渐增大，都为钻头处变形最大。（2）双向回转结构三阶模态振型为纵向振动，从钻头到固定外壳处变形都比较大。（3）单向回转结构三阶模态振型为扭转振动，变形从上至下逐渐变大，钻头外侧变形最大，内侧变形最小。（4）双向回转结构四阶模态振型为扭转振动，变形从上至下逐渐变大，内钻头变形较小，外钻头变形较大。（5）单向回转结构第四、五阶模态振型为一阶弯曲变形，结构中间和钻头处变形较大。（6）双向回转结构在第五、六阶的模态振型变为一阶弯曲变形，结构中间和钻头变形较大。（7）单向回转结构在第六阶的模态振型变为中间变形较大，两端变形较小。

由于高阶模态对整个结构的能量占比较小，故只提取两种结构的前六阶模态，得到的结构固有频率如表3所示。由于双向回转结构与单向回转结构均是对称结构，所以各阶模态会有重根出现，振型相同，频率也基本相近。结果显示除第三阶与第六阶模态，其他各阶固有频率双向回转结构都略高于普通单向回转结构，故钻进时双向回转结构更不易产生共振。

2.2 双向回转钻具结构的谐响应分析

钻进时，钻头的转动会引起钻柱的纵向振动，因而产生纵向交变应力；当井底对钻头旋转的阻力不断变化时会引起钻柱的扭转振动，因而产生交变剪应力。在两种交变应力的作用下，可将钻头与岩石的相互作用简化成周期函数激励［16］，通过谐响应分析计算出在相同频率及固有频率下的周期力作用下两种钻头的振幅大小，得到振幅与频率关系曲线。

图4 两种结构各阶模态的振型云图Fig.4 Vibration mode cloud charts of the two structures at each order mode

建立分析模型如图5所示，令双向回转和单向回转钻进结构的三维模型的轴线平行于z轴，即z轴方向为单向回转钻具结构和双向回转钻具结构的轴向，垂直于z轴的两个方向为结构的横向，简谐荷载的频率变化范围根据实际钻进时钻头的转速范围选择激励频率，金刚石钻头激励频率与转速的关系如式（6）所示［17］。

式中：f——激励频率，Hz；n——钻头转速，r/min。

根据岩心钻探规程按照金刚石孕镶钻头选取转速范围，结构中单向钻头的口径和双向钻头的外钻头口径都为128 mm，选取转速范围为260~520 r/min，由式（6）得出激励频率范围为4.33~8.67 Hz，因此将最低频率设置为0，最高频率设置为9 Hz。

边界条件：由于双向回转钻具结构在钻进时2个钻头会受到方向相反的扭矩，且由于传动比的影响，外钻头与内钻头受到的扭矩比为5∶3，对双向回转钻具结构的底部施加垂直向上、幅值为12 kN的钻压，对双向回转钻具结构内钻头施加幅值为61.2 N·m的扭矩，对外钻头施加方向相反、大小为102 N·m的扭矩。单向回转钻进结构底部施加向上的幅值为12 kN的钻压，同样施加幅值为61.2 N·m的扭矩。

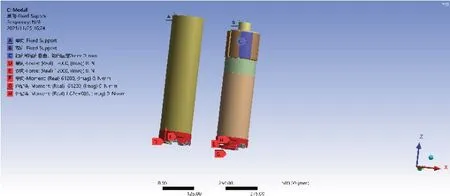
图5 模拟模型的建立Fig.5 Establishment of the simulation model

2种钻具结构在实际钻进激励频率范围下3个方向上振幅曲线如图6所示，由于2种钻具结构的一阶固有频率都大于所设置的激励频率范围0~9 Hz，所以振幅曲线上并没有出现峰值。从图6中可以看出双向回转钻具结构在x方向上的振幅小于单向回转钻具结构，在y方向上的振幅大于单向回转钻具结构，在z方向上双向回转钻具结构振幅和单向回转钻具结构相接近。从振幅曲线上看双向回转钻具结构没有明显的降低振动的作用。

图6 两种钻具结构的振幅曲线（0~9 Hz）Fig.6 Amplitude curves of the two drilling tool structures(0~9Hz)

2种钻具结构在实际钻进激励频率下产生的变形以及振型如图7所示，整体来看，2种钻具结构在4.33 Hz激励频率下的变形与在8.67 Hz激励频率下的变形基本相同，原因可能是激励频率远小于两种钻具结构的第一阶固有频率，不会发生共振的情况，即使频率有变化，结构的振幅变化也不大。两种钻具结构的振型都为纵向振动和扭转振动的耦合，从图中可以看出双向回转钻具结构的总变形要略小于单向回转钻具结构，双向回转钻具结构在z轴方向的变形与单向回转钻具结构差别不大，但双向回转钻具结构在x方向和y方向的变形都小于单向回转钻具结构，双向结构在x方向上的变形是单向结构的0.38倍，在y方向上的变形是单向结构的0.35倍，由此可以看出双向回转的钻具结构可以一定程度降低扭转振动的振幅。

3 结论

本文设计的双向回转钻具结构能依靠行星齿轮系驱动内外双层钻杆带动各自连接的钻头进行双向回转，能够独立发挥稳定钻掘性能、抵抗刀刃与地层摩擦产生回旋反作用力，提高钻柱的抗振效果。对结构的齿轮、密封、轴承等部分进行了校核设计，确定出机具尺寸。对双向回转钻具结构进行了振动模拟，并与在同等条件下普通单向回转钻进结构进行对比，结论如下：

（1）经校核，双向回转钻具结构密封系统最大能够满足2400 m井深的工况；最大能够满足12 kN的钻压；轴承系统能够满足正常钻井工况的需要。

（2）谐响应分析的数值模拟结果显示，在实际钻进参数的激励下，双向回转钻具结构发生扭转振动时x轴方向（钻具结构的径向）的变形与常规单向回转钻具结构相比降低62%，y轴方向（钻具结构的径向）的变形降低65%；双向回转钻具结构发生纵向振动时z轴（钻具结构的纵向）方向的变形与常规单向回转钻具结构相比降低3%。双向回转钻具结构发生扭转振动的振幅明显低于常规单向回转钻具结构，说明双向回转钻具结构能够有效抑制扭转振动。双向回转钻具结构对于纵向振动降低幅度较小，没有明显的抑制作用；从振幅曲线和两种钻具结构的总变形上看，双向回转钻具结构对于横向振动不具有抑制作用。

4 展望

同轴双向回转的钻头运动方式，能够通过内外钻头的相反方向运动，平衡各自与地层摩擦切削产生的扭矩，使钻柱所受扭矩趋于稳定，对影响钻柱结构稳定性和钻进效率较大的扭转振动具有较好的抑制作用。但钻头在井底钻进时钻头所受轴向力与扭矩均变化较大，齿轮和轴承工作环境较恶劣，容易损坏，因此该结构对于齿轮和轴承的强度要求较高。

图7 两种结构在简谐荷载（4.33、8.67 Hz）作用下产生的变形以及振型Fig.7 Deformation and vibration patterns of the two structures under the simple harmonic load(4.33Hz,8.67Hz)