捕获效应下基于比特检测的多分支树RFID 标签识别协议

张莉涓，范明秋，雷磊，王勇，袁代数

（1.南京航空航天大学电子信息工程学院，江苏 南京 211106；2.西南交通大学物理科学与技术学院，四川 成都 610031；3.中兴通讯股份有限公司，江苏 南京 210012）

1 引言

射频识别（RFID,radio frequency identification,）技术作为物联网感知层获取物品信息的重要关键技术之一，被广泛应用于各行各业，如仓储管理、物流追踪、药品监管和食品链监察等[1]。RFID 系统主要由一个或多个阅读器以及大量附着在物品上的电子标签组成，且每个标签拥有一个全球唯一的ID 信息（即EPC（electronic product code））。阅读器和标签通过询问应答方式通信，当有多个标签同时响应阅读器的询问请求时，标签信号发生碰撞，严重影响阅读器的识别性能[1-4]。合理的标签防碰撞协议可以有效提高识别性能，然而传统研究较少考虑捕获效应对识别过程的影响。

在被动式RFID 系统中，标签通过电感耦合或电磁反向散射方式获取能量并反馈响应信息。受信道衰落的影响，标签反馈信号强度差异较大。当有多个标签同时回复信息时，某一标签的信号强度可能远大于其他所有标签的信号强度之和，此时阅读器可以成功解码该标签的响应信息，该现象被称为捕获效应[5]。当捕获效应发生时，原本的碰撞时隙将转换为成功时隙，阅读器可以成功解码信号最强的标签信息，而其他强度较弱的标签信号将被覆盖，造成标签漏读，严重影响识别过程。

传统研究主要考虑捕获效应下Aloha 类标签防碰撞算法的识别性能优化问题。王阳等[6-8]提出的最大后验概率估计（CMAP,capture-aware maximum posterior probability estimate）算法采用贝叶斯对捕获概率和标签数量进行估计，并以此设置动态帧时隙Aloha 算法的最优帧长。Salah 等[9]则根据丢包率和捕获效应发生概率之间的关系获得不同信噪比条件下的捕获概率，并给出不同时隙长度和捕获概率影响下的最优帧长设置表达式。Nguyen 等[10]通过估计捕获概率和误检率来提高Aloha 算法的识别性能。总体来说，这类方法主要通过估计捕获效应发生的概率，调整帧长参数，增加成功时隙的比例，但没有考虑由捕获效应造成的标签漏读问题。

近年来，捕获效应下RFID 系统的可靠识别性能受到越来越多的关注。Wu 等[11]提出了捕获效应下基于查询树（QT,query tree）协议的隐藏标签处理方法，即通用查询树（GQT,general query tree）协议。该方法通过重复添加成功时隙相对应的查询前缀，获取隐藏标签的信息。但由于每个成功时隙所对应的查询前缀都执行了两次，识别效率较低。Lai 等[12]提出了通用树分裂（GBT,general binary tree）协议，通过阅读器发送确认信息静默已识别的标签，标记相应的隐藏标签便于下一轮识别，并通过多次执行该识别过程，解决标签漏读问题。采用类似的静默和标记方法，Choi 等[13]提出了捕获感知 CA-CRB（capture-aware couple-resolution blocking）协议识别隐藏标签，但是重复发送完整的ID 信息对标签进行静默和标记，增加了较多额外开销，识别时间长。Wu 等[14]结合Q 协议和二叉树协议提出自适应的ABTSA（adaptive binary tree slotted Aloha）协议，通过在成功时隙中回复随机数确认信息标记隐藏标签以减少通信开销，提高识别效率。

综上，已有研究主要基于传统的Aloha 或分支树协议解决捕获效应下的标签识别问题，识别过程中产生了较多的空闲时隙和碰撞时隙，且对隐藏标签的处理，增加的通信开销较多，整体识别效率低。本文通过设计合理的标签数量估计和高效可靠的标签识别算法来提高捕获效应下的标签识别效率。

在多数RFID 系统中，标签数量通常未知，合理的标签数量估计可以有效提高识别效率。传统的标签数量估计算法采用每帧中的时隙统计信息与理论预期值之间的关系对标签数量进行估计，时隙开销较大。为此，Chen 等[15]提出提前中断的估计方法，即在每帧中采用逐时隙估计的方式，提前结束帧长设置不合理的帧，减少时隙开销。随后Su等[16]提出设置固定检查点和离线表格方式，进一步降低计算复杂度。由于这类算法在前期获得的统计信息较少，估计不准确，所需时隙数较多。

在标签识别算法中，基于比特检测的树分支类算法具有较高的识别效率。Jia 等[17]提出的碰撞树（CT,collision tree）算法将发生碰撞的标签分成不相交的2 个子集，并通过比特检测技术获得每个子集中标签的最长共同前缀，从而消除空闲时隙。随后，Landaluce 等[18]提出的碰撞窗口树（CwT,collision window tree）协议采用启发式方法加速识别过程。Zhang 等[19]提出的多分支树碰撞（MCT,M-ary collision tree）协议将发生碰撞的标签分裂成多个子集，进一步缩短识别时延。但是，这些协议并没有考虑捕获效应对识别过程的影响。

为了有效提高捕获效应下标签可靠识别的效率，本文提出基于比特检测的多分支树标签识别（BMT,bit-detectingM-ary tree）协议，主要贡献如下。

1) 提出基于比特检测的快速标签估计算法，初步估计待识别标签的数量。通过将标签的随机选择信息融入标签回复信息中，提供标签数量估计统计信息，减少估计阶段的时隙开销。

2) 提出基于比特检测的多分支树标签识别协议。阅读器利用比特检测技术从标签回复信息中获取标签的时隙选择情况，有效消除空闲时隙，提高识别效率。并提出基于哈希静默的方法减少对隐藏标签处理的通信开销。

3) 建立多分支树概率模型分析BMT 的时隙开销和系统效率，并通过仿真对比从多方面验证BMT协议的有效性。

理论分析和实验结果充分证明了BMT 协议能够有效解决捕获效应造成的标签漏读情况，且相较于已有协议，BMT 协议的识别时间缩短了至少15%。

2 系统模型

考虑一个典型的静态RFID 系统，如图1 所示，该系统由阅读器、后端数据库和大量被动式标签组成。阅读器和所有标签共享无线信道，且在识别之前阅读器没有任何关于标签数量和ID 的先验信息。阅读器和标签之间采用询问应答模式进行通信，标签只有简单的计算、存储和通信能力，标签之间互不通信。与大多文献[6-14]中给定捕获概率的固定值不同，本文定义了被动式RFID 系统中的级联信道模型，以获取不同信道环境影响下捕获效应发生的概率，有效分析捕获效应对识别算法的性能影响。

系统的通信链路包括前向信道和反向信道2 个部分，阅读器通过前向信道发送查询命令并提供连续载波信号，标签通过反向散射方式从阅读器的载波信号中获取能量，并反馈回复信息[20-21]。阅读器收到的标签回复信号功率需综合考虑级联信道中前向和反向链路损耗。令Ptx为阅读器的发射功率，标签接收到阅读器信号的功率Pr,T为[20-21]

其中，ρL为阅读器与标签天线匹配的极化损耗因子（PLF,polarization loss factor），GR和GT分别为阅读器和标签的天线增益，L(df)为阅读器与标签相距df时前向信道的大尺度路径损耗，|hf|为前向信道的小尺度衰落随机系数。标签通过反向散射方式获取能量并回复，故阅读器收到某一标签的回复信号功率Pr,R为[20-21]

其中，τ为归一化系数，表示由编码和调制方法所导致的阅读器接收功率差异；μT为标签芯片与天线间的功率传输效率；上标和下标中的f 和b分别表示前向和反向链路，下标中的R 和T 分别表示阅读器和标签；Γ为标签反射系数差值。考虑自由空间路径损耗模型可得L(d)=[λ/(4πd)]2，链路衰落系数|h|可由Rician 分布或Rayleigh 分布模型获得。

根据功率模型，定义RFID 系统中的标签捕获效应如下：当有k个标签同时发送信号时，如果某一标签的信号强度远大于其他所有标签的信号强度之和，捕获效应发生，即

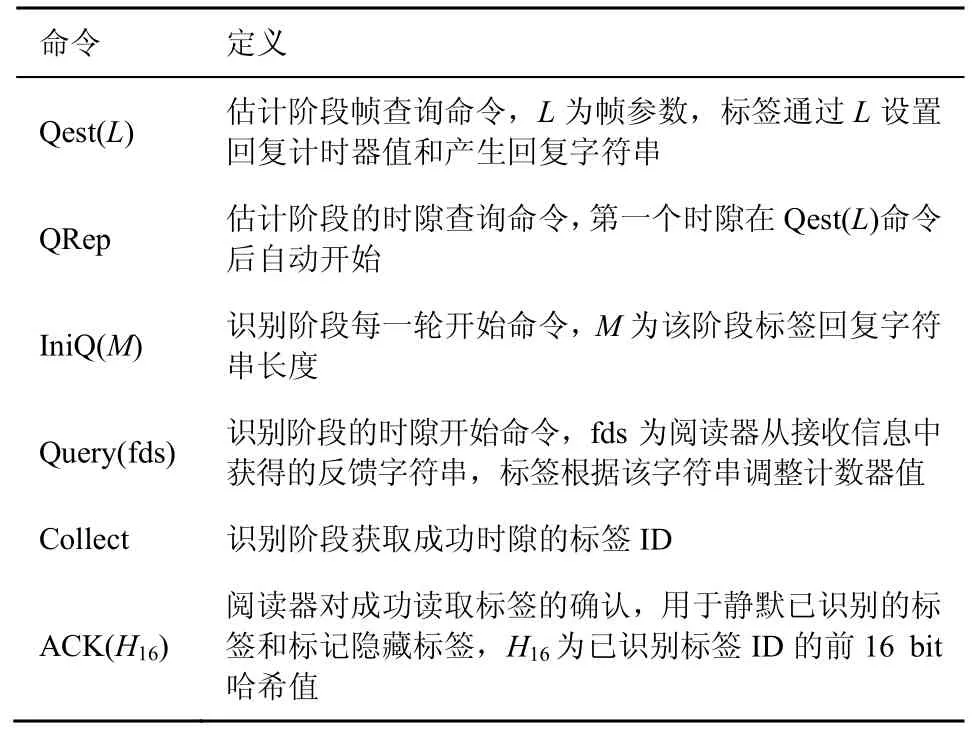
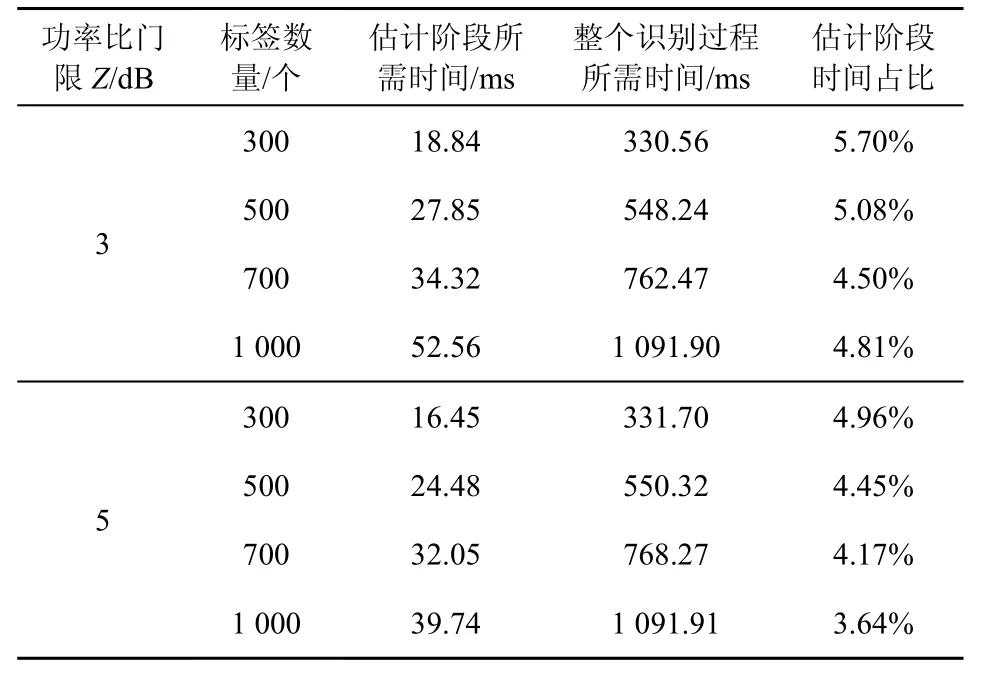
其中，Z为功率比门限（PRT,power ratio threshold）[5]，是阅读器成功接收信号所需要的最小载波干扰比，其值与调制方式和编解码方法有关，对于一般的窄带系统，1

由式(1)～式(4)可得，当有k个标签同时发送信息时捕获效应发生的概率qk。采用文献[20-21]中的射频参数设置，图2 给出了当阅读器的读取范围为3 m 时，不同参数条件下2 个标签同时发送信息的捕获概率。从图2 中可以看出，当Kf=Kb=−∞时，传输链路中缺乏可视通路，捕获效应发生概率较高；当Kf=Kb=10 dB 时，传输链路处于强可视环境，此时发生捕获效应的概率有所降低。

此外，从图2 还可以看到，随着功率比门限的增加捕获概率下降显著，因此本文主要分析功率比门限对捕获概率和识别算法的影响。考虑典型室内RFID 应用场景，图3 给出了当Rician 分布参数Kf=Kb=10 dB 时，捕获概率的理论值和指数拟合情况。

通过曲线拟合，可得捕获概率的近似表达式为qk=eaz+b，各参数如表1 所示。

表1 捕获概率拟合曲线参数

3 算法设计

本文提出的BMT 协议包括2 个阶段：基于比特检测的标签数量快速估计和多分支树可靠识别。在估计阶段，阅读器采用少量时隙对标签进行初步估计和预分组，该阶段采用帧时隙方式将时间分为帧，每一帧包括多个时隙。阅读器在每一帧开始时广播Qest(L)命令，告知所有标签当前帧参数L，该帧中的第一个时隙在该命令之后自动开始，其余时隙由阅读器的QRep 命令开启。在识别阶段，阅读器构造多分支树结构提高识别效率，该阶段通过逐时隙的方式进行识别，阅读器在每个时隙开始时广播Query(fds)命令通过fds 字符串反馈所有标签的时隙选择情况。表2 给出了BMT 协议用到的命令和定义。

表2 命令和定义

3.1 比特检测技术

在BMT 识别过程中，标签将其时隙选择信息融入回复信息中，阅读器通过比特检测技术从碰撞信息中获悉标签选择情况，以此对标签进行估计和识别。比特检测技术被广泛应用于RFID 标签防碰撞协议设计[17-19,22-26]，阅读器通过比特检测技术可以有效定位碰撞时隙中发生碰撞的比特位置。

比特检测技术可以通过曼彻斯特编码实现，该编码采用电平的跳变来表示“0”或“1”，即每个码元均用两个不同相位的电平信号表示[1]。如图4所示，采用电平下降沿表示“0”，上升沿表示“1”。当有多个标签同时回复信息时，阅读器可以定位到发生碰撞的比特位置[17-19,22-26]。图4 中标签A、B和C 分别回复字符串“10110010”“10100110”和“10000011”，通过曼彻斯特解码规则阅读器得到的字符串为“10XX0X1X”，其中“X”代表无效码元。阅读器可以有效解码全“0”和全“1”位的信息，但当有标签同时回复“0”和“1”时，阅读器判断该位置为碰撞位。

本文利用比特检测技术，设计标签回复信息和阅读器读取策略，有效提高识别效率。需要注意的是，比特检测技术主要用于碰撞时隙中碰撞信息位的获取，当某一时隙发生捕获效应后，该时隙变为成功时隙，阅读器可以成功解码接收到的信号，此时不会检测到碰撞位信息。

3.2 基于比特检测的标签数量快速估计

鉴于传统的估计方法所需时隙数较多、效率低，本文采用比特检测技术从标签回复信息中获取标签数量估计所需统计信息，减少通信开销。该过程采用帧时隙方式，阅读器在每一帧中估计标签数量和调整下一帧的帧参数，通过多个帧的调整和估计提高估计准确度。

在每一帧开始时，阅读器广播Qest(L)命令，其中初始帧的帧参数为L0。标签收到该查询命令后，产生1～L的随机数RN，然后设置时隙计数器tc和回复字符串str，其中，str 为B比特长字符串，且第 [(RN−1)modB]+1 位为“1”，其余位为“0”。其中，mod 为求模运算，为向上取整运算，B为标签在每个时隙中的回复信息长度，如图5(a) 中B=6。若tc=0，标签在当前时隙回复字符串str；否则，标签在收到阅读器的Qrep 命令时设置tc=tc−1。

阅读器接收标签回复信息并记录估计统计参数c0，直到当前帧中所有个时隙都执行完成。由于每个标签的回复信息中只有一位值为“1”，其他位都是“0”。结合比特检测技术，当阅读器检测到当前位为“0”时，表明没有标签选择当前位置。通过统计解码信息中“0”比特的数量，并将其与理论值相比，可得标签数量的初步估计。如果阅读器没有收到任何标签回复信息，如图5(a)中“时隙3”所示，该时隙为空闲时隙，阅读器设置c0=c0+B。如果阅读器收到标签的回复信息，则统计接收信息中“0”比特的数量，并设置c0=c0+。如图5(a)中“时隙1”为碰撞时隙，阅读器通过比特检测技术得到解码信息“0XX00X”，其中“X”为碰撞位，此时c0=c0+3；“时隙2”为成功时隙，阅读器接收信息为“000001”，故c0=c0+5。此外，图5 中t1和t2分别为阅读器和标签发送信息的传输时间，t3为空闲时隙中阅读器的等待时间。相较于传统标签数量估计算法在每个时隙只能获取单一的标签选择信息，本文算法在每个时隙可以获得较多标签选择信息，时隙利用率高。

在每帧结束时，阅读器根据c0值估计标签数量。每一帧中标签随机选择RN 值，与传统标签估计算法[6-10]类似，假定每个标签设置L比特中某位置为“1”的事件相互独立。则没有标签选择某一特定位置（即阅读器检测到比特“0”）的概率为P0=(1−1/L)n。实际统计中P0=c0/L，由此可得标签数量的估计值为

阅读器计算估计结果ñ与帧参数L的偏差|，并以此判断是否结束估计阶段。若未结束，阅读器调整下一帧的帧参数为当前估计值。

为了减少时隙开销，该阶段的结束条件由时隙开销和估计偏差之间的关系决定。图6 给出了当标签数量从100 变化到1 000 时估计阶段的时隙开销。从图6 中可以看到，随着标签数量和估计偏差的增加，估计阶段的时隙开销相应增加。当估计误差低于0.1 时，时隙开销的增加幅度变大，特别是当ε=0.01 时，时隙开销较大。为平衡时隙开销和估计准确度，设置估计阶段的结束条件为ε<10%。注意，该阶段主要给出标签数量的初步估计，为了降低算法复杂度，由捕获效应造成的估计偏差不作考虑。标签估计过程的伪代码如算法1 所示。

算法1基于比特检测的标签数量快速估计

阅读器端：

标签端：

3.3 基于比特检测的多分支树可靠识别

该阶段采用多分支树方法对标签进行识别，由于传统多分支树结构随分支数量的增加碰撞时隙数逐渐减少，而空闲时隙数急剧增加，整体识别效率低。本文通过比特检测技术将标签时隙选择信息融入回复信息中，通过反馈调整的方式消除多分支树结构中的空闲时隙，提高识别效率。

识别过程中，标签根据阅读器的Query(fds)命令调整时隙计数器tc。估计阶段结束时，阅读器根据最后一帧所有时隙中收到的标签回复信息构建L比特长反馈字符串fds，在fds 中用“1”表示有标签选择的位置（包括阅读器接收信息中所有碰撞位和“1”比特位），“0”表示没有标签选择该位置。如图5(b)中，假设估计阶段最后一帧中标签A～H选择的RN 分别为3,2,2,8,3,8,5,9，阅读器获得的fds=011010011。标签收到该反馈信息后更新其tc 值，即标签统计fds 中第RN 位之前的“0”比特数量b0，并设置时隙计数器值tc=RN−b0−1。图5(b)中，标签设置tc(A)=1,tc(B)=0,tc(C)=0,tc(D)=3,tc(E)=1,tc(F)=3,tc(G)=2,tc(H)=4。

若tc=0，标签产生新的随机数RN（RN∈[1,M]）和Mbit 全零字符串str，并将第RN 位设为“1”。该标签在当前时隙回复字符串str，其他标签等待阅读器的查询命令。图5(b)“时隙1”中标签B 和C的计数器值为0，于是在该时隙进行回复，回复字符串分别为“010000”和“000100”。阅读器收到标签回复信息后，若当前时隙为冲突时隙，则根据解码信息重新构建新的反馈字符串。图5(b)“时隙1”中阅读器接收到标签B 和C 的回复信息后，构建反馈字符串fds=010100。图5(b)“时隙2”中标签收到阅读器的Query(fds)命令后，按如下方式调整计数器值，

1) 若tc=0，标签统计fds 中第RN 位之前的“0”比特数量b0，并设置时隙计数器值tc=RN−b0−1。

2) 若tc>0，标签统计fds 中所有“1”比特数量b1，并设置时隙计数器值tc=tc+b1−1。

若当前时隙为成功时隙，阅读器接着发送Collect 命令获取相应标签的ID 信息。如图5(b)“时隙2”中在收到Collect 命令时，只有标签B 的时隙计数器值为0，此时标签B 回复其ID 信息，使阅读器可以成功识别该标签。

由于识别过程中可能发生捕获效应，阅读器无法判断成功时隙中有一个标签回复还是有捕获效应发生。为了解决由捕获效应造成的隐藏标签问题，阅读器在成功获取标签ID 后广播ACK(H16)信息，其中H16为已识别标签ID 的前16 bit 哈希值。收到该确认消息后，标签进行如下调整。

1) 若tc=0，对比其H16值是否与接收到的哈希值相等，若相等该标签转为静默状态，否则标记自己为隐藏标签，并等待下一轮识别。

2) 若tc>0，设置tc=tc−1，等待阅读器的查询命令。

阅读器重复后续时隙的识别过程，直到没有标签回复。采用阅读器回复ACK(H16)命令静默已识别标签和标记隐藏标签，可有效减少传统方法中需要传输完整ID 信息的时间开销。

阅读器在重复多轮该识别过程，读取所有标签的ID 信息。注意在后续每轮开始时阅读器广播第一个Query(fds)命令中fds 为空串，所有未被识别的标签收到该命令后设置tc=0，产生并回复字符串str。如果阅读器没有收到任何标签回复，则表明所有标签都被识别，便结束整个识别过程，该过程伪代码如算法2 所示。可以看到，标签在回复信息时需要产生特定的回复字符串，相较于传统算法中直接产生随机字符串，本算法会增加少量的计算开销。其次，在哈希静默过程中，标签需要进行哈希运算，但该过程只在已识别标签和隐藏标签中产生，故增加的计算开销在可接受范围内。

算法2基于比特检测的多分支树可靠识别

阅读器端：

标签端：

4 性能分析

本文提出的BMT 协议主要包括2 个阶段，标签数量估计和标签识别。标签数量估计阶段需要的时隙数较少，其时间开销占比将通过仿真结果给出，本节主要对标签识别阶段的时隙开销进行分析。对于捕获效应造成的隐藏标签，BMT 采用静默已识别标签的同时对其进行标记，以及多轮识别的方式保证可靠性。每一轮的识别过程基本相同，通过分析一轮中所需时隙数和识别标签数量之间的关系，可得所提协议的系统效率为

其中，n为标签数量，Thide(n)为单轮识别过程中由于捕获效应被隐藏的标签数量，S(n)为单轮识别过程所需总时隙数。

在识别阶段，阅读器首先根据估计结果对标签进行初步分组，令L1为标签初始分组数。依据相关文献[19,24,27]假定标签选择时隙服从均匀分布，n个标签中有k个标签被分配到L1个组中某一组的概率Pk可以由二项分布公式得到，即

在初始分组后，每一个发生碰撞的小组按照M分支的方式持续分裂。整个过程可以表示为如图7所示的多分支树结构，其中第一层的时隙数为初始分组数L1，第一层中每个碰撞时隙都将延伸为一棵M分支树。

在BMT 中，标签通过阅读器的反馈信息调整其时隙计数器值，及时消除即将产生的空闲时隙。故在单轮识别中所需时隙数即图7 中所有成功时隙和碰撞时隙数之和，即

其中，等号右边第一项为成功时隙数，第二项为由捕获效应产生的成功时隙数，第三项为碰撞时隙数，SA(k)为由初始分组中发生碰撞的时隙衍生出的多分支树所包含时隙数。采用递归方法可以得到SA(k)的表达式为

其中，等号右边第一项为该层中原本的成功时隙数，第二项为由捕获效应产生的成功时隙数，第三项为碰撞时隙数，每个碰撞时隙又将衍生出一个M分支的子树。由式(7)～式(9)可得每一轮中识别阶段所需时隙数。

接下来，分析单轮识别过程中的隐藏标签数。当k个标签同时回复发生捕获效应时，有k−1 个标签被隐藏和标记，并进入下一轮的识别过程。结合捕获效应概率模型，可得每一轮中被隐藏的标签数量Thide(n)为

其中，等号右边第一项为该层中发生捕获效应时被隐藏的标签数量，第二项为由该层碰撞时隙衍生出的M分支树中的隐藏标签数。采用类似方法可得

由此可得单轮识别过程中被隐藏的标签数量。综上，将式(8)和式(10)代入式(6)中可得识别阶段的系统效率。

5 仿真分析

仿真环境包括一个阅读器和多个被动式标签，且每个标签都有唯一的128 bit ID。阅读器和标签之间的数据传输率为160 kbit/s；表2 中的每个命令都用4 bit 表示；帧参数L，反馈字符串fds 以及哈希确认消息H16的长度都为16 bit；t1=t2=25 μs，t3=12.5 μs。采用MATLAB 2018a 进行仿真，且每个仿真结果都是500 次仿真的平均值。

在仿真分析中，首先对BMT 协议估计阶段的时间开销和总识别时间进行对比分析，其次给出功率门限比对BMT 协议识别性能的影响，最后分别对BMT 识别所有标签所需的碰撞时隙数和空闲时隙数以及平均识别时间进行分析。与捕获效应下标签识别最相关的同类协议进行比较，包括CMAP[8]、GQT[12]、GBT[13]和ASTSA[20]。其中，CMAP 是对捕获概率进行估计并优化动态帧时隙Aloha 识别过程的最优协议；GQT、GBT 和ASTSA 是考虑捕获效应下标签可靠识别的代表性协议。由于CMAP 只考虑单轮识别的情况，为了仿真对比的公平性，考虑将ASTSA 中的静默标记方法应用到CMAP 中，实现可靠识别。考虑识别性能在标签数量变化情况下的稳定性，本文给出Z=5 dB，标签数量从100 变化到1 000 时各协议的仿真结果。

5.1 估计阶段的时间开销

表3 给出了Z分别为3 dB 和5 dB 时BMT 协议在估计阶段和整个识别过程的时间开销对比情况。

表3 BMT 协议估计阶段的时间占比

表3 中估计时间和总时间随标签数量的增加而增加，而估计阶段的时间占比随标签数量的增加而减少。在BMT 识别过程中，标签估计阶段的时间开销非常少，且时间占比不超过6%。随着标签数量的增加，识别阶段的时间开销增加较多，而估计阶段增加的时间相对较少。因此随着标签数量的增加，估计阶段的时间占比有所下降。此外，随着Z的增加，估计阶段的时间占比随之降低。这主要是因为发生捕获效应的概率随Z的增加而降低，Z越大，发生捕获效应的情况越少；Z越小，捕获效应发生的情况越多，所以估计时间略长。

5.2 捕获效应对识别性能的影响

由系统模型分析可知，捕获效应发生的概率随Z值的增加而降低。考虑该门限值对算法识别性能的整体影响，图8 给出了BMT 协议识别500 个标签所需各类时隙数的变化情况。从图8 中可以看到，随着Z值增大，发生捕获效应的时隙数逐渐减少，这与图3 中捕获效应发生概率的变化趋势一致。其次，随捕获效应时隙数的减少，由碰撞时隙转化为成功时隙的数量随之减少，使碰撞时隙数相应增加。最后，由图8 可知随功率比门限的增大，识别所有标签所需总时隙数有增加趋势。

5.3 碰撞时隙数

当Z=5 dB 时，各协议碰撞时隙数随标签数量变化的仿真结果如图9 所示。

由图9 可知，碰撞时隙数随标签数量的增加呈线性增长，且本文提出的BMT 协议产生的碰撞时隙数最少，其次是CMAP 和ABTSA，而GBT 和GQT 产生的碰撞时隙数较多。相较于CMAP，BMT的碰撞时隙数减少了约40%。GBT 和GQT 通过传统的二叉树对标签进行分组，分裂速度较慢，且前期识别过程大部分为碰撞时隙，因此产生的碰撞时隙数最多。ABTSA 采用树时隙Aloha 的方式将标签分成多个组，适当减少了前期识别过程中的碰撞时隙数。但由于初始帧长与标签数量的不匹配，ABTSA 产生的碰撞时隙数仍然较多。CMAP 通过对标签数量和捕获概率进行估计，并以此调整帧长，产生的碰撞时隙数相对较少。BMT 通过多分支树的方式对标签进行分组识别，减少标签发生碰撞的概率，进一步减少碰撞时隙数。

5.4 空闲时隙数

各协议的空闲时隙数对比结果如图10 所示。图10 中，CMAP 产生的空闲时隙最多，GQT、ABTSA 和GBT 依次减少，BMT 协议几乎不产生空闲时隙。BMT 协议只有在估计阶段才产生空闲时隙，在识别阶段不产生空闲时隙。在估计阶段，如果没有标签选择当前时隙所对应的比特位，该时隙为空闲时隙。由表3 可知，估计阶段的时间占比非常小，因此该阶段产生的空闲时隙数也相对较少。在识别阶段，标签将时隙选择信息融入标签回复信息中，阅读器通过反馈检测到的标签时隙选择信息，使标签重新调整时隙计数器，消除空闲时隙。因此，BMT 产生的空闲时隙非常少。

GBT 根据标签的时隙计数器进行分组，产生的空闲时隙比其他协议少。ABTSA 根据估计结果动态调整帧长，产生的空闲时隙比GBT 略多。GQT受标签ID 分布影响较大，因此当ID 长度较长，标签数量相对较少时产生的空闲时隙较多。CMAP 考虑到空闲时隙比碰撞时隙和成功时隙的时间短，通过增大帧长设置减少碰撞时隙数，使空闲时隙数急剧增加，因此CMAP 产生的空闲时隙数较其他协议更多。

5.5 平均识别时间

最后，图11 给出了各个协议平均识别一个标签所需时间。从图11 中可以看到，本文提出的BMT协议平均识别一个标签所需时间最少，约为1.1 ms，ABTSA 其次，CMAP、GBT 和GQT 所需时间依次增加。由图9 和图10 可知，BMT 产生的碰撞和空闲时隙比其他相关协议都少，故平均识别时间最短。ABTSA 虽然比CMAP 产生的碰撞时隙多，但其产生的空闲时隙较CMAP 少得多，因此平均识别时间比CMAP 短。GBT 和GQT 产生了过多碰撞时隙，识别时间最长。相较于ABTSA、CMAP、GBT和GQT，BMT 的识别时间分别缩短了约15%、37%、50%和63%。

6 结束语

本文提出了基于比特检测的多分支树标签识别BMT 协议，该协议通过比特检测标签估计策略和多分支树标签识别算法对捕获效应下的RFID 标签进行高效可靠的识别，有效减少了标签估计和识别过程所需时隙数，缩短了识别时延。此外，本文还提出基于哈希静默的方法来减少静默已识别标签和标记隐藏标签的通信开销，进一步提高识别效率。理论分析和仿真对比表明，所提协议能有效提高识别效率，且相较于已有协议，所提协议将识别时间缩短了至少15%。在后续工作中，笔者将深入研究静默已识别标签和标记隐藏标签的有效方法，进一步提高识别效率。