基于时间光滑正则化的序列诊疗数据融合方法

郑 毅，胡祥培

大连理工大学 经济管理学院，辽宁 大连 116023

引言

医疗信息技术的飞速发展及其在医疗健康领域的普及给医疗服务行业的运营模式带来重大变革，特别是疾病诊断决策支持领域首当其冲[1]。诊疗大数据的多源性、动态实时更新性和高度医学专业性等特征给智能临床决策支持(特别是疾病预测分析)带来前所未有的机遇和挑战，使实现个性化和精准化医疗成为可能[2]。而如何充分利用诊疗数据，化解其内在的复杂性和数据规模并提供临床诊断决策支持，是未来该领域研究的关键问题[3]。因此，智能临床决策支持中诊疗数据融合方法的研究是当前学术界和产业界共同关注的热点和难点问题[4-5]。

大量已有诊疗数据分析方法往往只使用单一数据源进行分析建模[6]，由于慢性病患者诊疗周期长，患者电子病历中检查项目的测量值随时间推移数据不断更新[7]，利用单一阶段的数据源进行疾病预测分析难以刻画指标的动态变化特征，致使分析方法准确性降低[8]。目前，多阶段的诊疗数据融合研究中关于不同阶段诊疗数据源时间关联性的刻画缺少科学、有效的方法，使疾病预测滞后、诊断准确性和实时性受到限制。因此，如何实现序列诊疗数据有效融合和分析、提高诊疗大数据分析能力、实现准确的疾病诊断是亟待解决的问题。

综上所述，已有的序列诊疗数据融合方法难以刻画不同阶段诊疗数据的时间关联性，使疾病诊断准确性和实时性降低。为了有效解决疾病诊断中序列诊疗数据融合这一挑战性问题，本研究利用稀疏正则化原理，提出基于时间光滑正则化的序列诊疗数据融合(time smoothing regularization for sequential clinical data fusion,TSRSCDF)方法。该方法针对序列诊疗数据构建回归模型，利用稀疏正则化方法使特征级具有对指标的选择特性、数据源级能够保持不同阶段数据源具有时间连续性，最终实现对序列诊疗数据的融合，提高疾病诊断的准确性，增强疾病管理的有效性和科学性。

1 相关研究评述

疾病预测分析是指利用模型、算法和系统等信息技术对丰富的、大量的诊疗数据进行分析，得出未来与健康相关的结果或疾病风险信息，以提高诊疗决策水平[9-10]。关于疾病预测分析的研究主要包括疾病诊断和疾病预警[11]、再入院率预测[12]、医疗结果预测[13]和患者死亡率预测[14]等。

电子病历系统中患者的诊疗数据包含数值数据、文本数据、影像学数据等大量结构化和非结构化数据[15]，数据的非结构化特性给数据融合过程带来巨大困难，采用特征级融合能够很好地克服数据异构性障碍[16]。但不同阶段诊疗数据包含的海量特征信息使模型构建和参数求解更加复杂，因此，本研究将详细介绍特征级融合方法的相关研究以及保持不同阶段数据源的时间连续性对于序列诊疗数据融合建模带来的挑战。

基于特征的融合方法[17]过程为：首先，对各数据源数据进行预处理，将其转换为特征向量；其次，将各数据源数据对应的特征向量按次序串联，构成合成特征向量；最后，通过数据融合算法实现多数据源的融合。由于诊疗数据的高度复杂性，合成特征向量具有高维特征[18]，为了避免诊疗数据融合过程中过拟合，国内外学者对诊疗数据融合中的特征高维问题开展了大量研究，主要分为两类。一类方法采用先降维再融合的思路，CORREA et al.[19]采用奇异值分解降维法对数据源特征向量分别进行降维，再利用多集合典型相关分析将医疗影像学中两类影像数据与一类数值数据进行融合，并很好地关联三类数据的空间分辨率和时间分辨率，进而提高数据分析的准确性。另一类是在构建目标函数时采用稀疏正则化约束改进学习模型，其本质是在构建模型中进行特征选择，以降低模型相关特征维度，代表方法有Lasso正则化方法[20]、组Lasso正则化方法[21]等。ADHIKARI et al.[22]研究高维纵向数据分类问题，将其方法应用于心血管健康认知研究中，利用纵向数据诊断患者阿尔茨海默病的病情，实验结果证明了该方法的有效性，并得出与病情相关的重要影响要素；LI et al.[23]使用稀疏逆协方差估计对348名受试者的多模态诊疗数据进行分析，预测患者阿尔茨海默病的病情，得到的模型在诊断准确性上高于仅使用单一诊疗数据源进行疾病诊断的方法。利用基于稀疏正则化理论构建的数据融合模型，具有灵活刻画数据源间与特征间关系的优势，同时模型具有特征选择的特性，使模型具有更好的可解释性[24]。

由于序列诊疗数据源具有时间关联性，考虑不同阶段数据源具有的时间关联特性，实现采用基于稀疏正则化的序列诊疗数据有效融合、提高诊疗数据分析的准确性是一个具有挑战性的研究方向。针对具有多阶段的诊疗数据融合问题，其中有代表性的方法有：XIE et al.[25]提出利用疾病不同阶段的序列检查信息和诊断信息，将不同阶段的诊疗数据按照时间顺序串联构成合成向量，利用合成向量构建回归模型，预测疾病状态的序列数据建模方法；CHEN et al.[26]提出在数据预处理过程中利用时间光滑核函数，对不同阶段数据赋予不同权重值，刻画不同阶段指标的时间重要性，将多阶段数据转换为点模型表示的方法；安莹等[27]针对心血管疾病的准确预测问题，提出利用循环神经网络等技术融合多种类型的临床数据，并有效捕获电子病历数据中的时序特征，最终提高心血管疾病风险预测的性能。但是上述方法仍难以科学准确地描述多阶段的诊疗数据融合研究中关于不同阶段诊疗数据源的时间关联，且存在实际使用中诊断准确性较低的问题，因此需要使用准确性更高的方法刻画多阶段诊疗数据融合中的时间关联性。

基于稀疏正则化的序列诊疗数据融合过程存在以下困难。①对于序列诊疗数据融合中不同阶段诊疗数据源时间关联性的刻画。建立相应的稀疏正则化模型，使不同阶段数据源具有的权重因子随时间变化，诊疗数据中相同特征的权重因子随时间的变化具有连续性和一致性。②对于序列诊疗数据融合中合成特征向量的处理。序列诊疗数据合成特征向量具有高维性，因此需要在构建序列数据融合模型时对模型进行降维处理，并在不同阶段数据源中选择相同特征，以提高模型泛化能力和可解释性。③高效的数值优化算法设计。由于引入稀疏正则化项，使模型参数的优化求解问题不具有解析解，因此需要针对模型特征设计高效的数值求解算法[28]。为了有效解决上述困难，本研究构建基于时间光滑正则化的序列诊疗数据融合模型以及设计高效求解算法，并利用阿尔茨海默神经影像学计划[29]中序列磁共振成像检查数据，针对阿尔茨海默病进行疾病诊断，以验证方法的有效性。

2 基于时间光滑正则化的序列诊疗数据融合方法

针对目前关于序列诊疗数据融合问题研究存在的不足和挑战，本研究提出基于时间光滑正则化的序列诊疗数据融合方法。先介绍采用回归分析构建的序列诊疗数据融合模型，在此基础上在模型训练过程中构建时间光滑正则化罚函数，刻画不同阶段诊疗数据源的时间关联性，建立基于时间光滑正则化的序列诊疗数据融合模型。由于提出的模型难以数值求解，本研究采用近端加速梯度下降优化算法[30]对模型进行求解。

2.1 理论基础

假设诊疗数据为具有n个阶段的序列数据x1,x2,…,xt,…,xn，xt为第t阶段的检查特征，为m维实数向量，xt∈Rm，R为实数向量集，m为各阶段检查特征的维度，第(n+1)阶段对应的诊断结果为y，y∈{+1,-1}。本研究采用回归模型构建疾病诊断模型，假设当前阶段为n，记X为特征矩阵，X=[x1;x2;…;xn]T∈Rn×m，T为矩阵的转置。患者第(n+1)阶段诊断结果的患病预测模型为

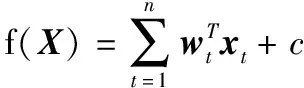
(1)

其中，wt为对于xt的权重向量；c为截距，c∈R；wt和c皆为需要求解的参数。针对(1)式最直接的求解方法为利用逻辑损失函数[31]进行参数拟合，即

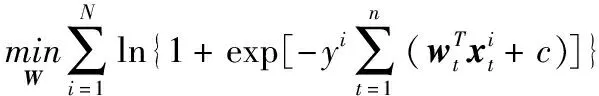
(2)

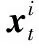
利用(2)式进行的参数拟合未能考虑不同阶段特征的时间关联性，导致针对序列诊疗数据融合分析的精确性难以提升。

2.2 基于时间光滑正则化的序列诊疗数据融合模型

为了刻画序列诊疗数据融合中不同阶段特征的时间关联性，在(2)式拟合参数模型的基础上，采用结构化稀疏的方法构建时间光滑正则化罚函数，使同一特征相邻阶段的权重系数差别较小，进而保证预测结果的连续性和一致性，提高方法对于疾病诊断的准确性。具体模型为

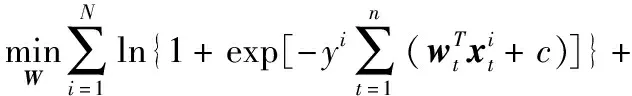
(3)

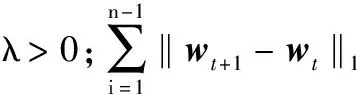
由于序列诊疗数据合成特征向量具有高维性，使通过(3)式拟合的预测模型难以处理“维度灾难”问题，致使模型泛化能力降低，处理高维特征的预测问题一般采用降维方法。为了使模型具有可解释性，采用结构化稀疏的方法对合成特征向量进行降维处理，模型学习过程中构建基于l2,1范数的组Lasso正则化罚函数[32]，使预测模型能够利用不同阶段序列诊疗数据中的相同特征进行疾病诊断。结合时间光滑正则化罚函数，得出具有时间光滑正则化罚函数的序列诊疗数据融合模型，即

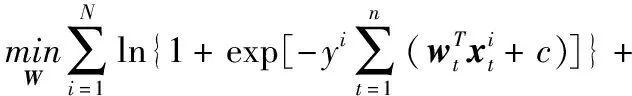
(4)

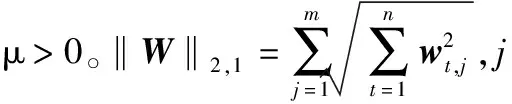
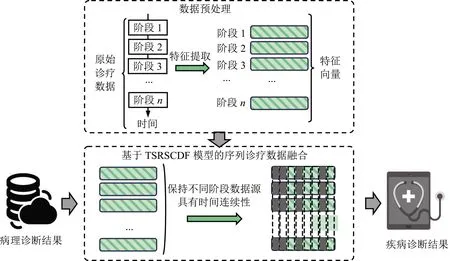
图1 TSRSCDF模型进行疾病诊断流程

2.3 求解TSRSCDF模型的近端加速梯度下降优化算法

由于TSRSCDF模型中包含组Lasso和融合Lasso两类正则化罚函数，使模型不可微，求解光滑优化问题的经典算法难以适用；同时，由于逻辑损失函数具有的复杂形式，使模型难以解析求解。

针对TSRSCDF模型的求解，一种思路是采用对偶原理构建辅助变量和约束条件，将(4)式等价地转换为带约束的光滑优化问题，然后利用凸优化算法进行数值求解[34]。TIBSHIRANI et al.[33]针对具有融合Lasso罚函数的最小平方误差优化问题，引入辅助变量将模型重构为具有线性约束和非负约束、目标函数为光滑函数的约束优化问题，然后针对等价优化问题采用SQOPT软件包进行求解。AHMED et al.[35]针对具有融合Lasso罚函数的逻辑回归问题，引入辅助变量构建等价优化问题，并对等价问题采用CVX优化软件包求解。然而此种方法求解效率较低，TIBSHIRANI et al.[33]认为，当样本量大于200、样本维度高于2 000时，此算法不能有效求解问题。因此，提出近端加速梯度下降法对TSRSCDF模型进行高效求解。

由于加速梯度下降算法是针对求解非光滑优化问题具有收敛阶最高的二阶梯度下降求解方法[36]，本研究采用加速梯度下降算法框架设计优化算法。记

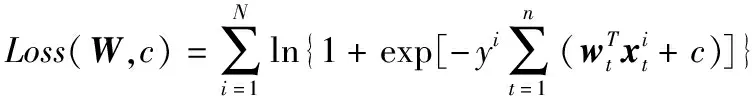
(5)

其中，Loss(·)为训练数据的经验误差损失函数，则TSRSCDF模型可化为

(6)

首先，构建目标函数f(·)在点(W,c)的近似为

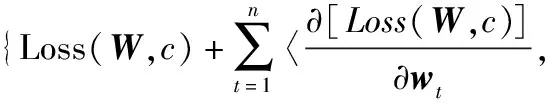
(7)

其中，U为具有n×m维变量矩阵，U=[u1;u2;…;ut;…;un]T∈Rn×m，ut为权重向量wt的近似，t=1,2,…,n；d为截距，d∈R，R为实数集；L为Loss(·,·)二阶导数的近似值，L>0；‖U-W‖F为矩阵U-W的F-范数。由于(7)式是关于(6)式的近似，因此目标函数(7)式的最优解可作为目标函数(6)式的最优解的近似，导出针对(6)式的梯度下降迭代求解算法，即

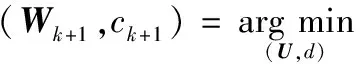
(8)

其中，k为迭代次数，Wk为n×m维变量矩阵，Wk∈Rn×m；ck为常量，ck∈R；Lk为搜索步长。

加速梯度下降算法迭代过程中产生两组序列：{(Wk,ck)}为解近似值，{(SWk,sck)}为搜索方向，{(SWk,sck)}为(Wk-1,ck-1)和(Wk,ck)的线性组合，即

(SWk,sck)=(Wk,ck)+βk(Wk-1,ck-1)

(9)

其中，SWk为n×m维变量矩阵，SWk∈Rn×m；sck为常量，sck∈R；βk为组合参数。因此，加速梯度下降算法的近似值更新算法为

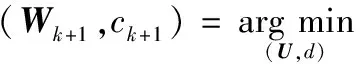
(10)

基于Armijo-Goldstein规则[37]计算Lk，优化问题(10)式是求解TSRSCDF模型(6)式的关键，下面给出利用近端算子[38]对该问题的求解方法。

记(6)式的近端算子为

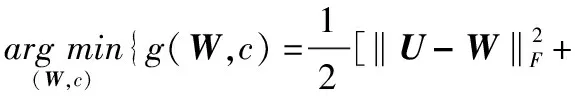
μ‖W‖2,1}

(11)

(11)式可视为(6)式中的Loss(W,c)为平方误差的特殊形式。为了利用(11)式求解TSRSCDF模型，下面推导出优化问题(10)式与优化问题(11)式最优解的联系，见定理1。

定理1 优化问题(10)式的最优解(Wk+1,ck+1)可由优化问题(11)式导出，即

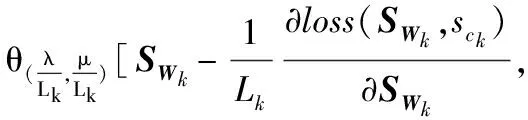
(12)

证明：首先，将等式右侧的算式按照定义展开；其次，将优化函数中的2-范数展开并合并同类项；最后，分别按照fLk,(SWk,sck)(W,c)和(Wk+1,ck+1)定义推导出左侧表达式。具体推导过程省略，如有需要可与作者联系。

由定理1可得，优化问题(10)式的最优解可由求解优化(13)式问题得出，即

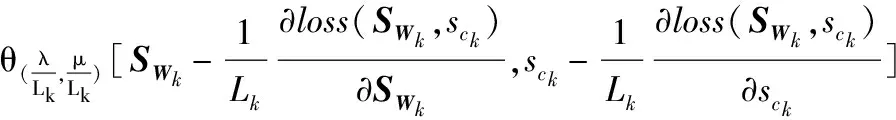
(13)

利用LIU et al.[39]提出的融合Lasso信号近似优化算法对优化问题(13)式进行求解。具体地，由于(13)式是具有融合Lasso和组Lasso两项罚函数的投影算子，可将计算分为两步，第一步利用FLSA优化算法对子优化问题进行求解，有

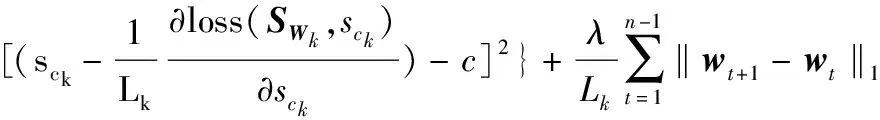
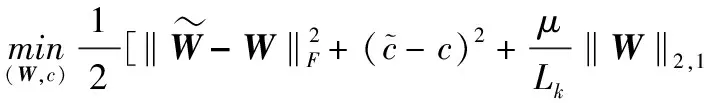
(14)

则上述优化问题的最优解即为(13)式的最优解。

至此，本研究给出求解TSRSCDF模型的近端加速梯度下降优化算法，具体如下：

输入：W0,c0,L0>0,λ>0,μ>0

输出：W,c

初始化：k=1,W1=W0,c1=c0,α-1=0,α0=1,L=L0(α为算法内部变量计算的特定参数)

重复

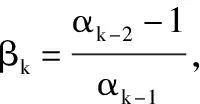
查找最小L=2pLk-1,p为任意实数，p=0,1,…，使f(Wk+1,ck+1)≤fL,(SWk,sck)(Wk+1,ck+1)成立，其中，

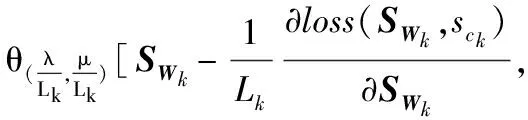
直至|f(Wk+1,ck+1)-f(Wk,ck)|⟸ TOLERANCE*|f(Wk,ck)|成立

首先初始化各参数的值，然后逐步迭代求解W和c的值。每一次循环中按照加速下降策略确定搜索方向(SWk,sck)，逐渐增大搜索步长L的值，并利用f(Wk+1,ck+1)≤fL,(SWk,sck)(Wk+1,ck+1)条件确定搜索步长，逐步更新参数，直至相邻循环中目标函数值差值的绝对值满足精度，终止循环，并输出最优解。

3 实验设计和结果分析

本研究选取阿尔茨海默病进行疾病诊断，验证基于序列诊疗数据融合的疾病诊断方法实际效用。本研究数据来源于阿尔茨海默神经影像学计划数据库[29]中837名患者的核磁共振检查数据，每个核磁共振检查数据样本包括患者的白质分解体积、皮层分割体积、表面积、皮质厚度平均值和皮质厚度标准差5类检查特征指标[40]，共350项检查指标及患者的病理诊断结果。将患者第一次检查的时间点称为基线(baesline,BL)，其后不同阶段的检查数据按照相对于基线的时间间隔进行标注。例如，M06表示该检查对应的时间阶段是第一次检查后的6个月。患者的序列检查数据时间间隔为{BL,M06,M12,M18,M24,M36,…… }。

实验中本研究将利用TSRSCDF模型融合序列诊疗数据，对下一阶段患者病情进行预测，从而达到诊断疾病的目的。患者的病理诊断结果分为痴呆-正类和正常-负类共两类，采用受试者工作特征(receiver operating characteristic,ROC)曲线测量预测的性能[41]。ROC曲线是以假阳性概率为横轴、真阳性概率为纵轴组成的坐标图，有

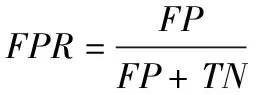
(15)

(16)

其中，FPR为假阳性概率，FP为假正的样本数目，TN为真负的样本数目，TPR为真阳性概率，TP为真正的样本数目，FN为假负的样本数目。由于ROC曲线并不能直观比较模型的预测性能，需根据ROC曲线下的面积(AUC)作为标量指标测量模型的预测性能以及量化模型均衡Ⅰ类错误与Ⅱ类错误的能力[42]。

实验共分为3部分，第1部分对比TSRSCDF方法与单阶段诊疗数据分析方法的预测性能，说明基于序列数据融合的疾病诊断方法预测性能上的优势；第2部分比较TSRSCDF方法与相关序列诊疗数据分析方法的预测性能；第3部分比较利用相同序列诊疗数据针对未来不同阶段疾病诊断的预测性能，分析预测时间窗长度对于模型预测性能的影响。

3.1 实验1：对比TSRSCDF方法与单阶段诊疗数据分析方法的预测性能

首先用本研究提出的TSRSCDF方法融合3个阶段诊疗数据，对患者第4阶段的病情进行预测，通过利用TSRSCDF方法对诊疗序列{BL,M06,M12}进行分析，对患者下一阶段即M18的病情进行预测。为了实际验证疾病预测模型的有效性，对初始数据集进行筛选，选择诊疗序列{BL,M06,M12}中各阶段诊断结果为健康的患者数据，预测M18阶段患者患病状况。最终得到223名患者的序列诊疗数据，其中M18阶段健康人数为191人，患病人数为32人。

单阶段诊疗数据分析方法为：①采用具有Lasso正则化罚函数的线性回归方法，利用M12阶段的诊疗数据预测M18阶段患者患病状况；②基于多任务学习的疾病预测方法[8]，利用BL阶段的诊疗数据，构建M18阶段患者患病预测子任务。TSRSCDF方法中的正则化参数λ∈{10-7,10-6,10-5,10-4,10-3}，μ∈{2-9,2-8,2-7,2-6,2-5}；具有Lasso正则化罚函数的线性回归方法中的正则化参数μ∈{2-9,2-8,2-7,2-6,2-5}，基于多任务学习的疾病预测方法中的融合Lasso正则化参数μ∈{2-9,2-8,2-7,2-6,2-5}。各方法中正则化参数的取值通过交叉验证确定[43]。随机选择80%的数据作为训练数据集合，利用学习模型对余下的测试数据进行分类。重复实验并计算ROC曲线下面积的平均值，当试验重复50次后，预测结果平均值对于逐步增加的试验次数趋于稳定，因此采用将试验重复50次并计算ROC曲线下面积的平均值的做法，TSRSCDF方法与单阶段诊疗数据分析方法的预测性能见表1，黑体数据表示ROC曲线下面积的最高值。各方法对应的ROC曲线见图2。

表1 TSRSCDF方法与单阶段诊疗数据分析方法的预测性能对比

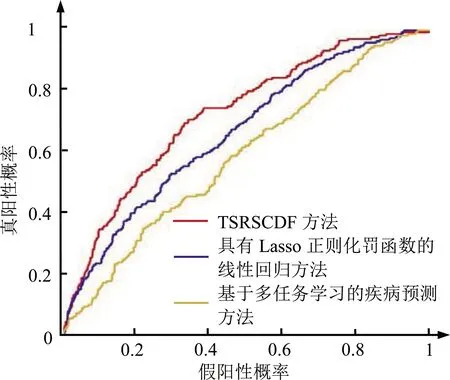
图2 TSRSCDF方法与单阶段诊疗数据分析方法对应的ROC曲线

由表1可知，由于TSRSCDF方法利用检查指标对应不同阶段的更多特征构建疾病诊断模型，因此具有较高的预测性能。利用单阶段诊疗数据的疾病诊断方法中，相对于基于多任务学习的疾病预测方法，利用具有Lasso正则化罚函数的线性回归方法具有较高的预测性能，因为基于多任务学习的疾病预测方法利用BL阶段的诊疗数据，对M18阶段患者患病状况进行预测，而采用具有Lasso正则化罚函数的线性回归方法利用M12阶段的诊疗数据进行病情预测，由于预测时间窗较长，利用BL阶段的诊疗数据进行的病情预测难以准确刻画疾病的进展状况导致预测准确性降低。图2中TSRSCDF方法对应的ROC曲线整体高于其他方法，也说明TSRSCDF方法具有较高的预测性能。实验1的结果表明，与利用单阶段诊疗数据的病情预测方法相比，本研究提出的利用序列诊疗数据融合的疾病诊断TSRSCDF方法，在构建疾病诊断模型时将不同检查指标对应的不同阶段检查值同时进行分析，选择相关指标的不同阶段特征值进行融合，这一数据融合机理使TSRSCDF方法具有综合各检查指标中信息变化的优势，最终提升了疾病诊断的准确性。

3.2 实验2：对比TSRSCDF方法与相关序列诊疗数据分析方法的预测性能

TSRSCDF方法具有的突出特性是模型学习过程中使同一特征相邻阶段的权重系数差别较小，进而保证预测结果的连续性和一致性。为了验证利用TSRSCDF方法对提升疾病诊断准确性的作用，对比的相关序列诊疗数据分析方法为：①采用具有组Lasso正则化罚函数的线性回归方法；②将多阶段诊疗数据转换为点模型表示[26]，对转换特征利用具有Lasso正则化罚函数的线性回归方法。利用与实验1相同的样本数据，3类方法利用诊疗序列{BL,M06,M12}数据对患者M18阶段患者患病状况预测结果进行对比。TSRSCDF方法中的正则化参数λ∈{10-7,10-6,10-5,10-4,10-3}，μ∈{2-9,2-8,2-7,2-6,2-5}；具有组Lasso正则化罚函数的线性回归方法中的正则化参数μ∈{2-9,2-8,2-7,2-6,2-5}；将多阶段数据转换为点模型表示方法，并对转换特征利用具有Lasso正则化罚函数的线性回归方法中的正则化参数μ∈{2-9,2-8,2-7,2-6,2-5}。各方法中正则化参数的取值通过交叉验证确定。随机选择80%的数据作为训练数据集合，利用学习模型对余下的测试数据进行分类。重复实验50次并计算ROC曲线下面积的平均值，TSRSCDF方法和相关序列诊疗数据分析方法的预测性能见表2，黑体数据为ROC曲线下面积的最高值。各方法对应的ROC曲线见图3。

由表2可知，TSRSCDF方法比相关序列诊疗数据分析方法具有较高的预测性能。图3中TSRSCDF方法对应的ROC曲线高于其他方法，也说明TSRSCDF方法具有较高的预测性能。由于TSRSCDF方法中检查指标对应不同阶段特征的权重值由机器学习确定，选取的权重值更加准确地刻画指标变化的规律，且时间光滑正则化罚函数使相同指标不同阶段权重值具有一致性，因此相对于对点模型表示特征[26]利用具有Lasso正则化罚函数线性回归的疾病预测方法具有较高的预测性能。3类方法中，具有组Lasso正则化罚函数的线性回归方法具有最低的预测性能，因为该方法在分析序列诊疗数据时未能考虑不同阶段诊疗数据源的时间关联性，进而难以准确刻画指标随时间变化的特征。

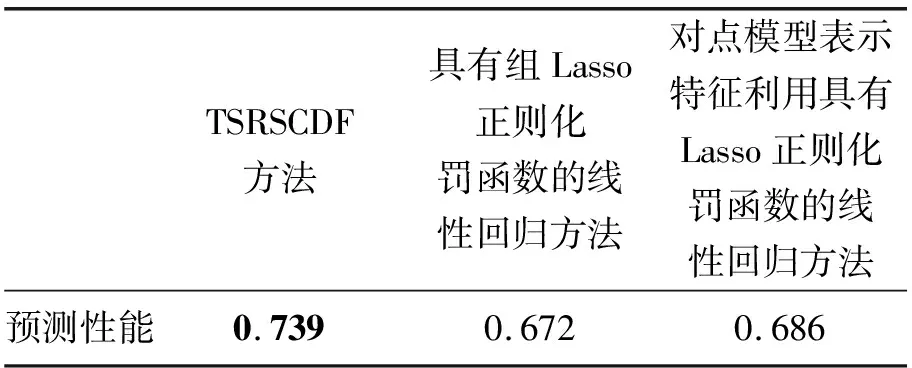
表2 TSRSCDF方法与相关序列诊疗数据分析方法的预测性能对比

图3 TSRSCDF方法与相关序列诊疗数据分析方法对应的ROC曲线

3.3 实验3：预测时间窗长度对于疾病诊断准确性的影响

实验3旨在探讨预测时间窗长度w对TSRSCDF方法和相关序列诊疗数据分析方法疾病预测准确性的影响。分别利用各方法融合诊疗序列{BL,M06,M12}数据，预测患者M18阶段、M24阶段、M36阶段、M48阶段和M60阶段患病状况。针对不同阶段的患病状况预测，由于患者的检查序列具有不同的长度，需将实验1使用的样本数据进行筛选，得到针对不同阶段病情预测实验利用的数据，详见表3。

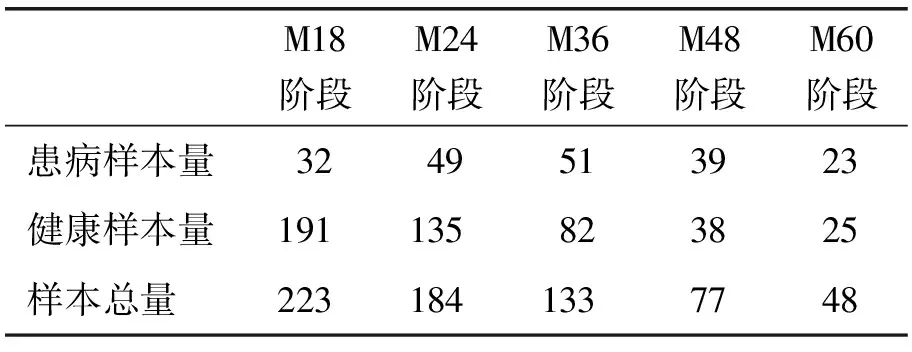
表3 针对不同阶段患病状况预测实验利用的数据

预测不同阶段患者患病状况的实验中，TSRSCDF方法中的正则化参数λ∈{10-7,10-6,10-5,10-4,10-3}，μ∈{2-9,2-8,2-7,2-6,2-5}，正则化参数的取值通过交叉验证确定。随机选择80%的数据作为训练数据集合，利用学习模型对余下的测试数据进行分类。重复实验50次并计算ROC曲线下面积的平均值，不同阶段患病状况的预测性能见表4。

由表4可知，①预测时间窗越长，模型的预测性能越低。TSRSCDF方法对患者M18阶段和M24阶段的患病状况预测具有较高的预测性能，对于具有较长时间窗的疾病预测性能有所降低，但是整体上TSRSCDF方法针对各个阶段患者的患病状况预测具有相对稳定的预测性能。②针对M18阶段和M24阶段患病状况预测实验，对比两组实验中类标签的分布和分类的结果，说明TSRSCDF针对M18阶段处理分类结果具有类不均衡特征的预测问题具有较好的预测性能。③与相关序列诊疗数据分析方法的预测性能相比，TSRSCDF方法针对不同阶段患病状况预测的ROC曲线下面积值的标准差(σ=0.030)最小。结果表明，采用序列数据融合的TSRSCDF方法的疾病诊断结果具有稳定性。

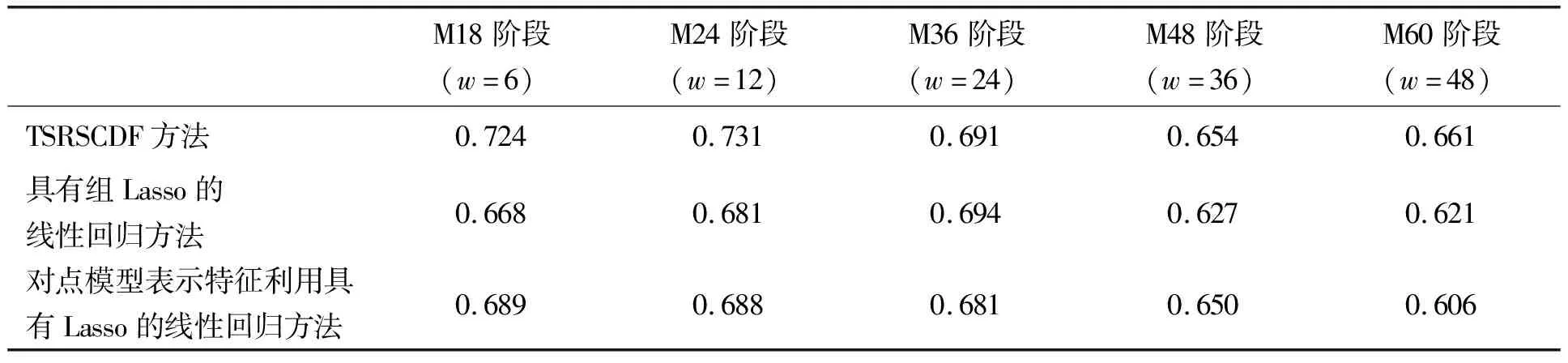
表4 TSRSCDF方法与相关序列诊疗数据分析方法针对不同阶段患病状况的预测性能对比

4 结论

本研究探讨疾病诊断中序列诊疗数据融合问题，针对序列诊疗数据融合中多个阶段的诊疗数据时间关联性刻画难、合成特征向量降维难和序列诊疗数据融合模型求解难等问题，提出将结构稀疏性与不同阶段诊疗数据源的时间关联性有机结合，采用序列诊疗数据融合思想的疾病预测分析研究思路，构建基于时间光滑正则化的序列诊疗数据融合方法。

针对阿尔茨海默病进行疾病诊断实验，利用真实诊疗数据进行实验分析，将本研究提出的TSRSCDF方法与传统单阶段诊疗数据分析方法相比，表明本研究构建的TSRSCDF方法在疾病诊断上具有优越性；与相关序列诊疗数据分析方法的预测性能对比结果表明，TSRSCDF方法构建的时间光滑正则化罚函数保证了模型具有刻画不同阶段诊疗数据源的时间关联性特征，同时采用结构化稀疏，使该方法具有较高的预测性能和可解释性；实验结果进一步表明，预测时间窗长度对于疾病诊断性能的影响及TSRSCDF方法疾病诊断性能具有鲁棒性。

该方法可以推广到实际阿尔茨海默病的早期诊断中，提高了智能临床决策支持系统识别高风险患者的能力，为科学地实施慢性病患者疾病管理提供决策支持，进而提高患者生命质量；同时弥补了传统诊疗数据分析未能科学、准确地刻画指标变化趋势导致诊断准确率较低的不足，为开展个性化和精准医疗提供决策支持。

慢性病患者诊疗数据对应于每个阶段检查数据具有多源的特征，在未来研究中将进一步针对多源诊疗数据的融合方法进行深入研究，完善诊疗数据融合分析方法，丰富智能临床决策支持系统研究体系，并将研究结果应用于脑卒中和脑血管疾病等相关慢性疾病的诊断，进一步验证本研究提出的方法在慢性疾病诊断中的普适性和实用价值，并拓展相关应用研究。