公开基于BP神经网络的飞行器参数辨识与自适应控制*

杨广慧 杜立夫 李 辉 刘旭东

北京航天自动控制研究所， 北京 100854

0 引 言

近年来，各类复杂航空飞行器、航天飞行器的结构和任务需求日益复杂，对其控制性能(包括精确性、稳定性、抗干扰性和收敛速度等)的要求越来越高[1]。由于跨域空间飞行器飞行高度和飞行马赫数跨度大、飞行环境复杂，特别是高超声速临近空间飞行器在飞行过程中气动和气热特性变化剧烈[2-3]，飞行器所受的气动力及力矩的数学模型复杂，非线性程度强，很难获得其精确的解析表达形式。因此在飞行过程中，如果能够实时辨识出飞行器的气动特性及参数，不仅能增强系统的鲁棒性与适应性，还可以有效提升控制精度。

神经网络自提出以来，在模式识别、感知学习、模型建立与智能控制方面取得了巨大发展和应用[4-5]。神经网络可以任意精度逼近非线性系统的输入输出特性,是一种非线性系统辨识建模的有效工具[6-7]。用其作为非线性系统辨识模型,可以较好地解决复杂非线性系统的辨识建模和辨识问题。目前应用较为广泛的、比较成熟的神经网络为反向传播(Back Propagation，BP)神经网络，是人工神经网络中较为典型的一种前馈网络，特别适合处理系统的非线性、不确定性以及逼近系统或结构特性的辨识函数等问题[8-9]。刘晓东等人[10]运用基于BP神经网络的模型参考自适应控制方法设计姿态控制器，采用模型参考自适应控制的基本设计框架，通过BP神经网络对PID控制参数进行自主调节，实现控制器的输出逼近参考模型的输出，完成自适应控制设计，确保飞行器姿态控制系统的性能指标，但飞行性能需要依赖参考模型的选取，本文采用BP神经网络对飞行器关键参数舵效系数b3进行辨识，根据b3调节比例增益，运用已知的吹风气动数据离线训练神经网络即可，不需依赖其他模型的选取，具有工程实用性。朱海洋等人[10]提出基于径向基(Radial Basis Function，RBF)神经网络的容错控制方法，利用RBF神经网络，在线辨识并补偿火箭动力学模型中控制量以外的变化值，有效解决发动机推力下降故障下姿态稳定的问题，本文BP神经网络相比于RBF神经网络结构简单，且利用离线进行神经网络参数计算，可以有效解决计算效率慢的问题。

工程上常采用自适应增益PID的控制方法，由于其可靠性高，结构简单且易于实现等优点，是飞行器广泛采用的一种控制形式。想要取得很好的控制能力，就需要精确调整自适应增益参数，结合BP神经网络的任意逼近特性，根据飞行器的气动数据离线训练BP神经网络，在飞行过程中根据该神经网络进行实时气动关键参数的辨识，并将辨识结果应用到控制系统自适应调参中，最终提高控制性能。

1 BP神经网络

1.1 BP神经网络结构

BP神经网络属于有监督的学习网络，是简单的多层神经网络，也是人工神经网络中最具代表性的一种网络模型。它是由非线性变化单元组成的一种前馈型网络，一般由3个神经元次组成，即输入层、隐含层和输出层，其中输入层和输出层各一个，隐含层可以有多个。各层的神经元之间形成权互连接，而同一层次内的神经元之间无连接。因此，每一层的神经元只对前一层神经元输入敏感；每一层神经元的输出只影响下一层的输出。BP神经网络结构如图1所示。

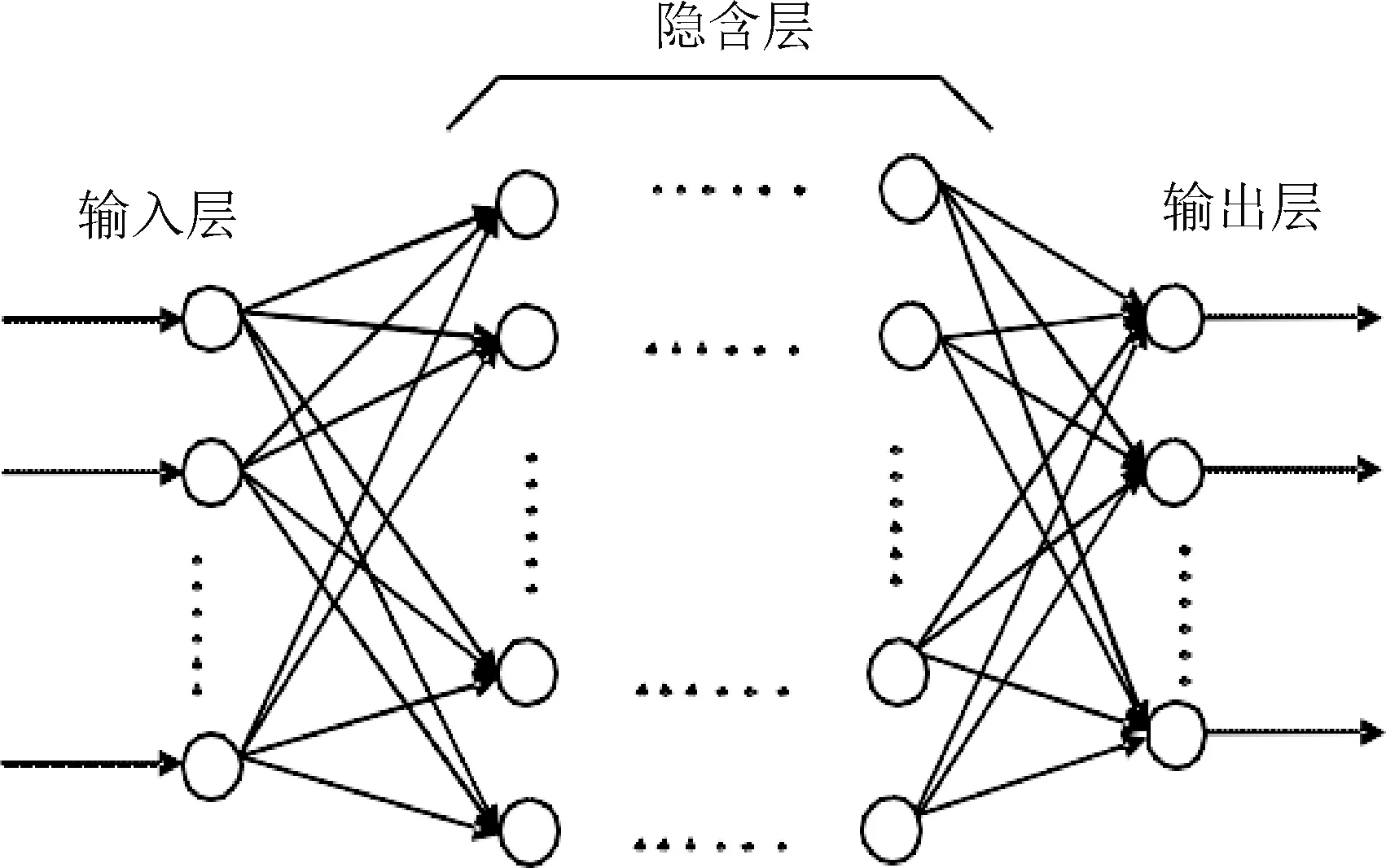
图1 BP神经网络结构图

输入层：用来表示网络的输入个数，其处理单元数目依据具体问题而定。

隐含层：用来表示输入处理单元间的交互影响，均使用非线性转换函数。

输出层：用来表示网络的输出个数，其处理单元个数依据实际问题而定，使用非线性转换函数。

实际应用中，BP网络输入层的节点数由训练样本X=(x1,x2,…,xn)的维数n决定，同样输出层的节点数由输出向量Y=(y1,y2,…,ym)的维数m决定。已经证明，对任何在闭区间内的连续函数，都可以用1个三层的BP网络(即含有一个隐含层)逼近，1个3～4层的BP神经网络可以完成任意的n维到m维的映射。

1.2 BP神经网络算法

BP算法是一种迭代算法，每一次学习过程由输入数据的正向传播和误差的反向2个过程组成，其过程可以描述如下。

1)输入信号正向传播

输入信号从输入层经由隐含层，传向输出层，在输出层输出信号，这是输入信号的正向传播。在信号向前传播的过程中，网络的权值不变化，每一层神经元的状态只影响下一层神经元的状态。如果在输出层得不到期望的输出，则转入误差反向传播。

多层网络某一层的输出为下一层的输入，可描述为

Am+1=Fm+1(Wm+1×Am+Bm+1),
(m=1,2,…,M-1)

(1)

其中，M为网络层数，第一层为输入P。

定义误差函数

(2)

2)误差信号反向传播

网络的实际输出与期望输出之差即为误差信号，误差经由输出层开始逐层向前传播，这是误差信号的反向传播。在误差信号反向传播程中，网络的权值由误差反馈进行调节。通过权值的不断修正，使网络的实际与期望输出更加接近。

利用梯度下降法求权值变化。

(3)

其中η为学习速率。

2 基于BP神经网络的参数辨识与控制器设计

2.1 飞行器神经网络的参数辨识

以某跨域空间飞行器为例，气动参数非线性严重，俯仰通道小偏差方程为

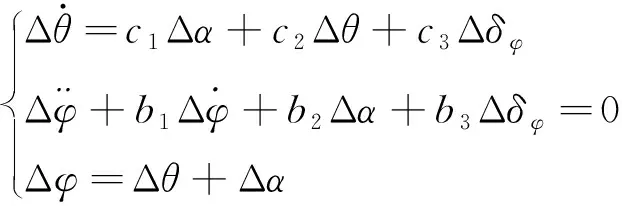
(4)

其中,c1为攻角系数，c2为弹道倾角系数，c3为俯仰舵的等效力系数，b1为阻尼系数，b2为静稳定系数，b3为俯仰舵的等效力矩系数，此处不再给出小偏差方程系数的具体形式。

在训练中，输入量P为3个(马赫数，攻角和侧滑角)，输出量A为1个(俯仰力矩系数)。选择3个输入，1个输出，每层为15神经元的两层隐含层结构，其中隐含层激活函数为双曲线正切S型函数，输出层激活函数为线性函数，训练数据样本为336行数据。

经过大量的学习训练，得到满足指标的神经网络参数见式(5)。训练结果见图2。

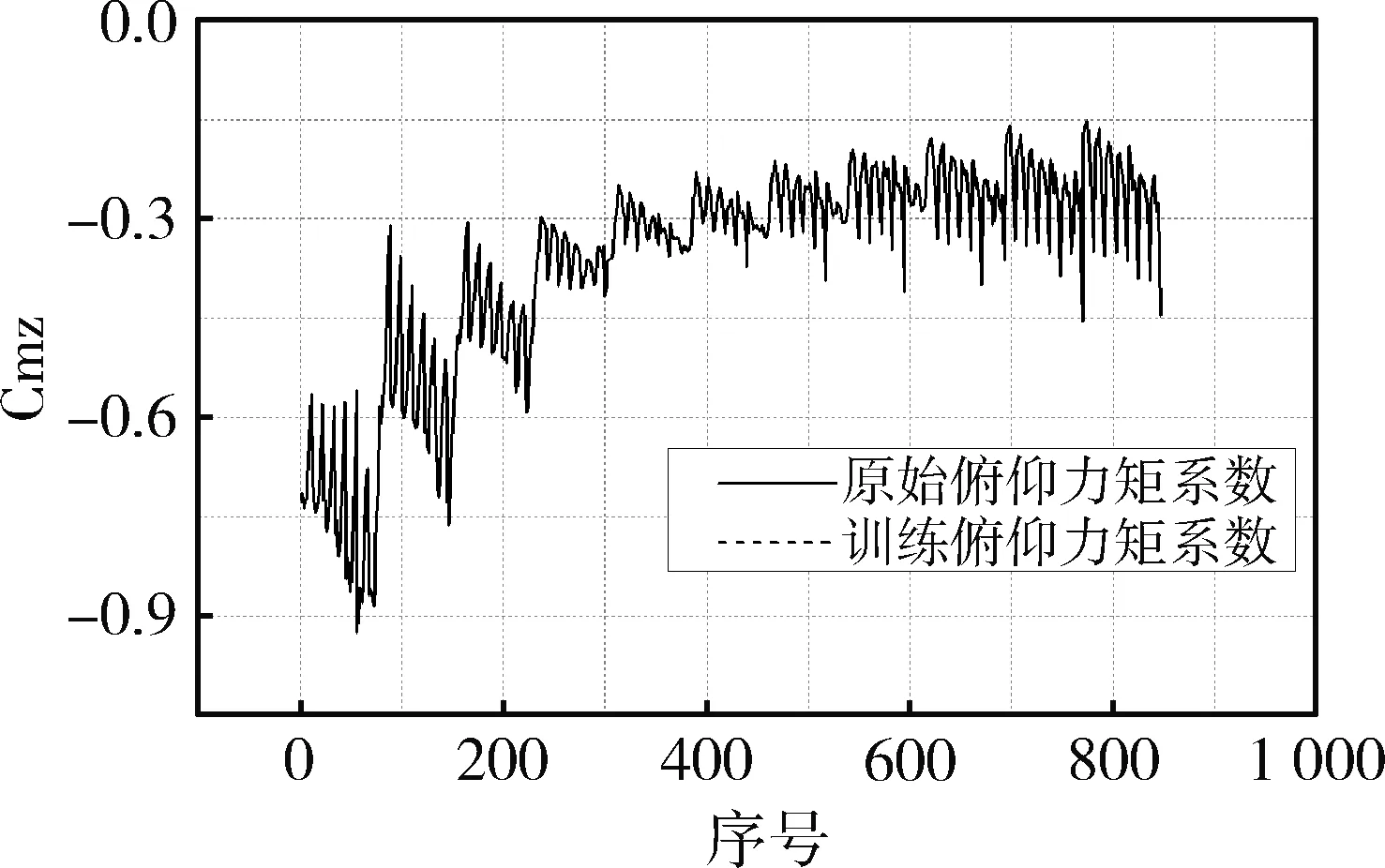
图2 BP神经网络训练结果与原始数据比较

(5)

其中F1，F2和F3是激活函数；W1，W2和W3为神经元连接权值；B1，B2和B3为偏差量。

训练完成后，W1为[15×3]矩阵、W2为[15×15]矩阵、W3为[1×15]矩阵。B1为[15×1]矩阵、B2为[15×1]矩阵、B3为[1×1]矩阵。得到的网络参数可以用于在线辨识气动参数，在飞行过程中，只要输入马赫数，攻角和侧滑角，按上述的公式即可计算出俯仰舵的力矩系数b3，见图3所示。

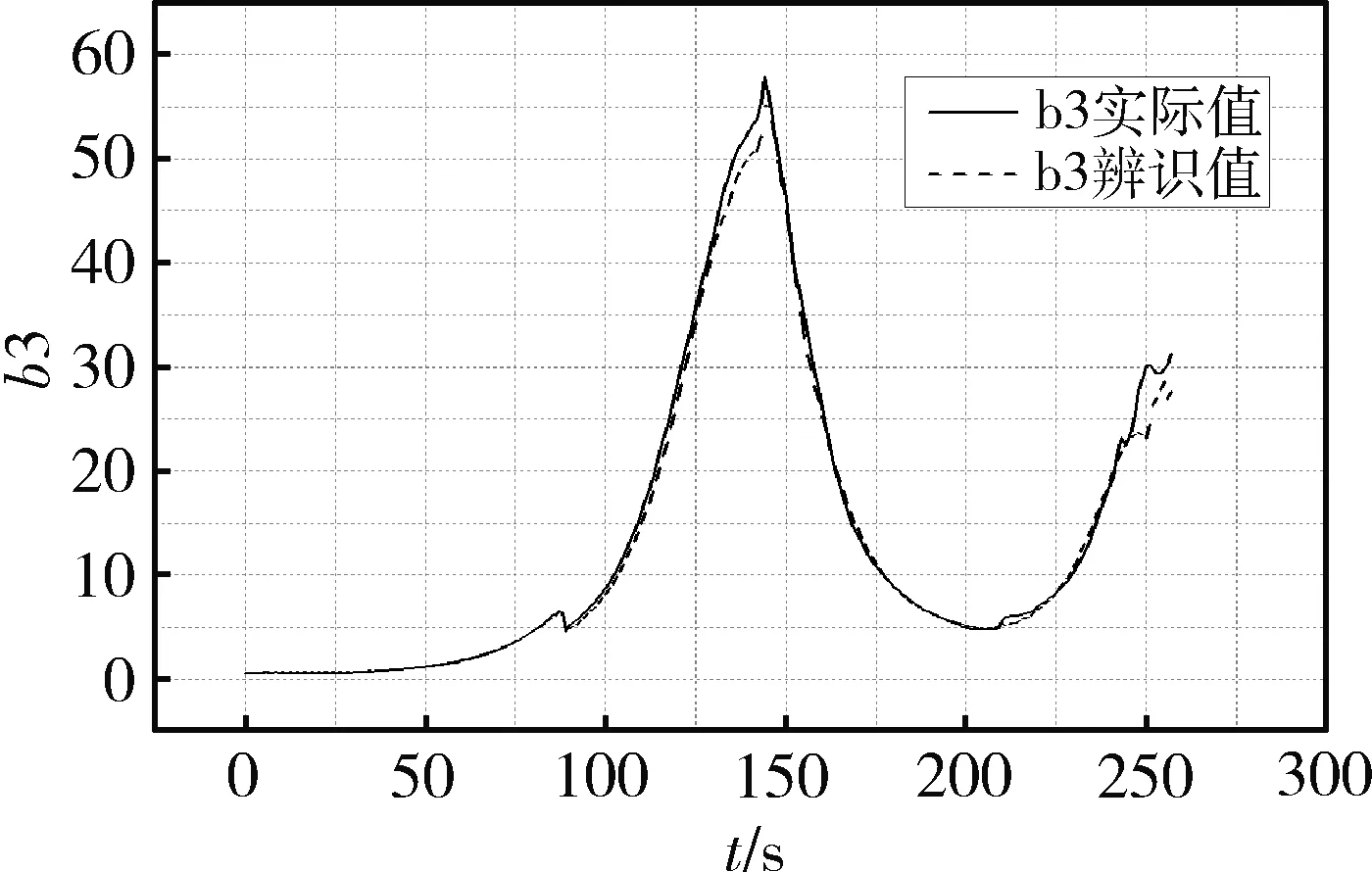
图3 飞行参数b3实际值与辨识值

2.2 自适应PID控制器设计

根据辨识值进行自适应PID控制律设计，其增量PID控制律设计为如下形式：

u(k)=u(k-1)+Δu(k)

(6)

Δu(k)=kp[e(k)-e(k-1)]+kie(k)+
kd[e(k)-2e(k-1)+e(k-2)]

(7)

式中，u(k-1)与u(k)为上一拍与目前拍的控制量，Δu(k)为目前拍控制增量，e(k)、e(k-1)和e(k-2)为目前拍与前两拍的姿态跟踪误差；kp，kd和ki分别为PID控制律的比例系数、微分系数和积分系数，其中kp为根据辨识b3得到自适应控制增益，即kp=1/b3。

飞行控制框图如图所示，控制增益根据离线训练的神经网络参数进行实时变化。

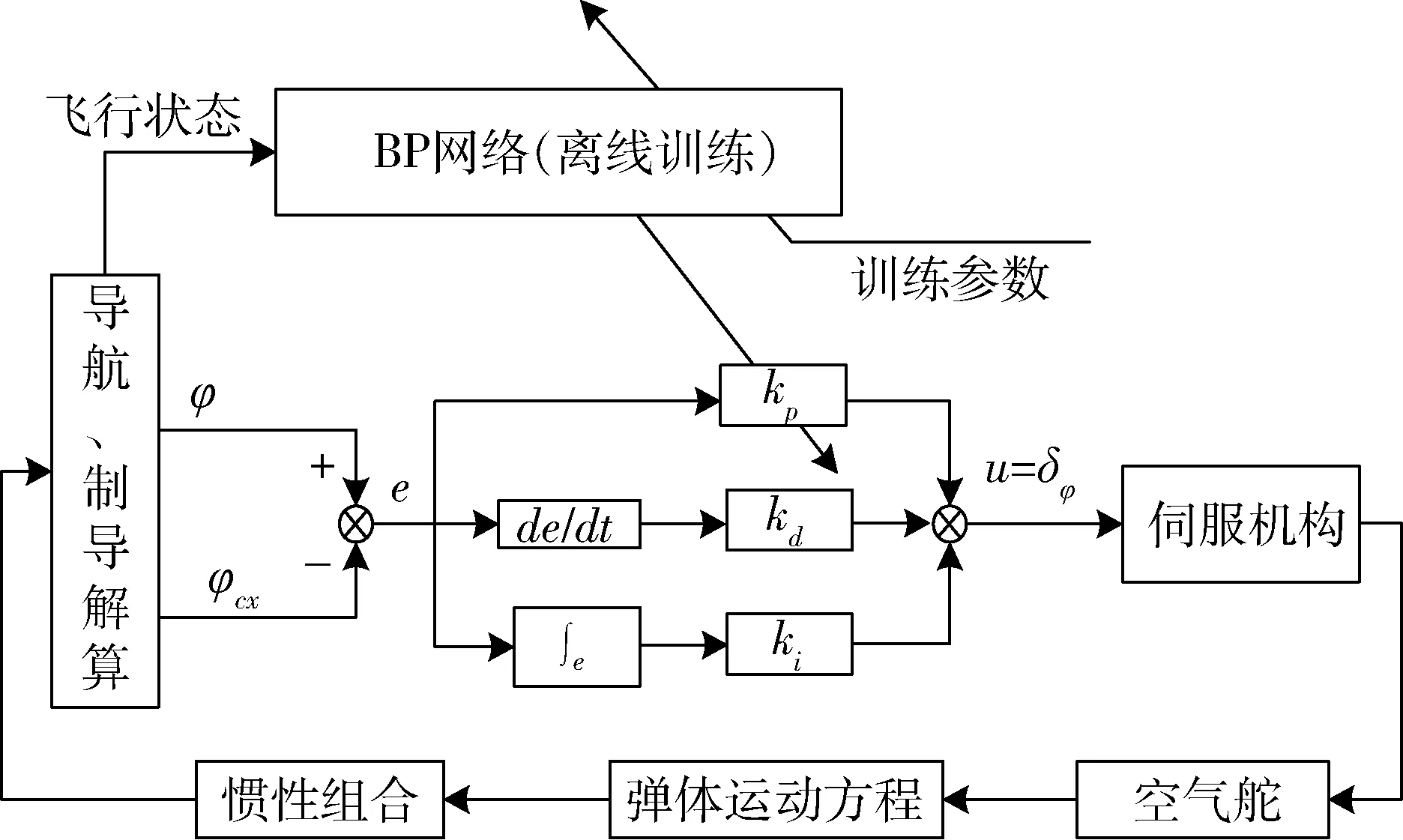
图4 基于BP神经网络的飞行控制框图

3 仿真校验

对某飞行器进行六自由度数学仿真，仿真选取飞行器对象的相关初始参数为：

初始高度H0=50 km，初始马赫数Ma=6.5，初始攻角α=0°、初始侧滑角β=0°；控制参数中的微分系数为kd=0.5，积分系数为ki=0，比例系数随飞行状态自适应变化。神经网络离线训练完成，得到训练好的神经网络参数。将该网络载入到飞行器自适应姿控系统中，根据当前的飞行参数在线实时计算出控制增益即控制参数kp。仿真结果曲线如图5所示。

图5 飞行器自适应控制增益曲线

图5为飞行器从初始状态到落地飞行过程中自适应增益的变化过程，随着飞行器舵效自适应变化，图6为在飞行过程中飞行器俯仰姿态角跟踪俯仰程序角的过程，图7为使用其他方法计算的控制增益与本方法的比较曲线，可以看出由于飞行空间跨度非常大，舵效在整个飞行过程中变化范围非常大，对舵效的辨识保证了姿态角快速稳定的跟踪效果，控制效果良好。

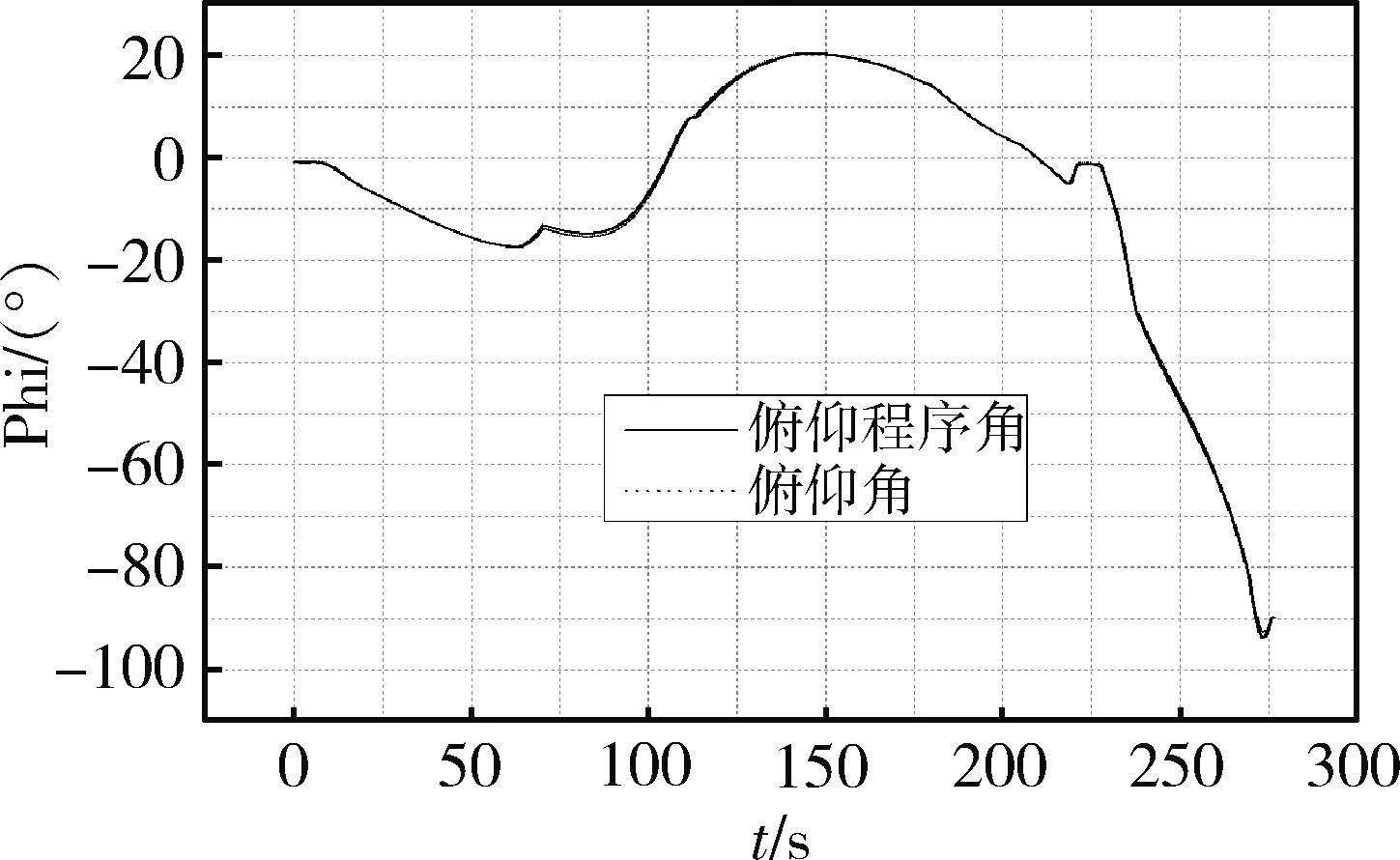
图6 飞行器俯仰姿态角跟踪曲线

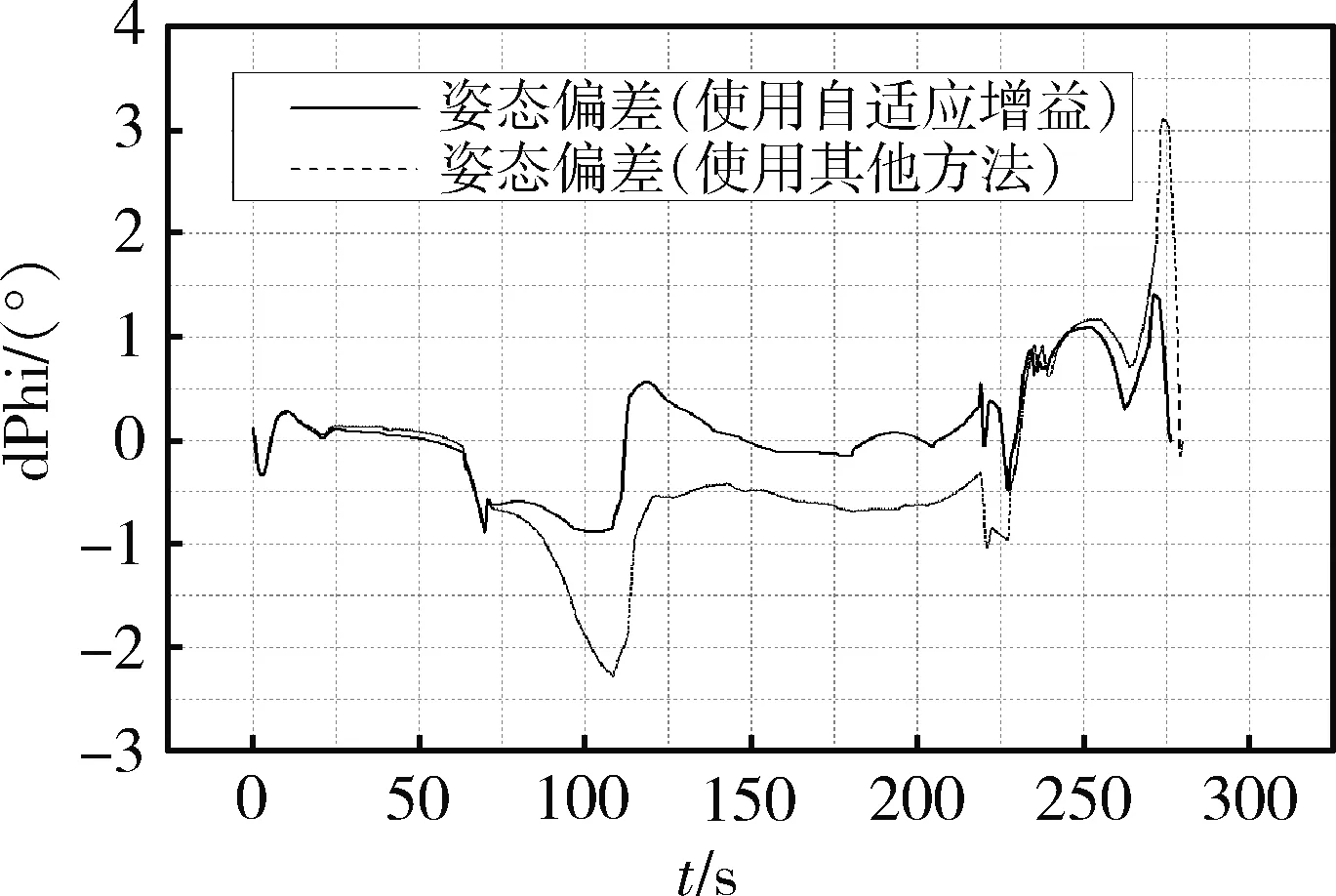
图7 飞行器俯仰姿态角偏差比较

4 结 论

研究了基于BP神经网络的飞行器参数识别与自适应控制，首先给出了BP神经网络的网络结构和算法，结合BP神经网络的任意逼近特性，对气动参数进行离线训练，利用神经网络训练的结果进行飞行器舵效参数实时辨识，采用自适应PID控制方法，根据辨识结果进行在线调整自适应控制增益，最终进行六自由度数学仿真，仿真结果验证了该方法正确性与有效性，结果表明飞行器飞行稳定，跟踪效果良好，具有一定工程实用价值。