市政道路钢弹簧浮置板对地下空间结构的减振影响

陈 伟，邹锦华，霍文斌，王 健，邬龙刚

(1. 广东省建筑设计研究院有限公司,广东 广州 510010；2. 广东工业大学土木与交通工程学院,广东 广州 510006)

0 引言

随着城市的快速发展，城区道路密集，土地资源紧张，市政道路汽车荷载引起的环境振动及噪音问题引起了广泛的关注，对居民的日常生产生活带来严重影响，容易引发人们的身体健康问题[1]。如何有效地减小交通荷载引起的低频振动，已经成为重要的研究热点。

目前对于交通荷载引起环境振动的隔振研究较多，徐平等[2]通过研究无量纲位移等值线、无量纲位移变化曲线等进而分析了屏障后不同位置、剪切模量、桩间距和入射频率对非连续弹性圆柱实心桩屏障的隔离效果的影响。陈锋和黄茂松[3]利用阻抗函数研究填充沟的厚度, 深度以及填充材料相对周围土体的阻抗比的隔振效果。陆建飞和聂卫东[4]应用 Biot理论和积分方程的方法，研究了频域内饱和土中的单桩在瑞利波作用下的动力响应。廖雪娇等[5]对连续墙挡板进行三维数值模拟分析，研究了5～20 Hz 荷载下混凝土桩组成的不同尺寸挡板的减振效果, 并与日本某现场试验结果比较。

浮置板是城市轨道交通中最为有效的轨道减振降噪结构，目前国内外关于浮置板轨道减振降噪已有颇多研究成果。如：Lombaert等[6]通过有限元方法建立了浮置板轨道模型，研究了软硬2种土质下的动力响应。TSUTOMU等[7]研究了浮置板轨道系统支撑刚度对行车安全性和舒适性的影响。姚京川等[8]通过Ansys对浮置板轨道结构的减振效果进行分析。谷爱军等[9]建立了钢弹簧浮置板轨道系统的三维模型，研究了不同参数及激振频率对结构的传递特性和隔振效果。丁德云等[10]通过室内试验与有限元模拟相结合，研究了简谐荷载作用下浮置板轨道的加速度响应和振级损失。孙晓静等[11]通过Ansys对钢弹簧浮置板轨道系统进行了模态和谐响应分析，并采用Sperling指标进行了舒适度评价。耿传智等[12]对浮置板轨道系统进行了三维有限元模态分析，研究了浮置板密度、尺寸、扣件和支座刚度、支座间距等参数变化对轨道系统固有频率的影响和钢轨挠度、位移和加速度的变化规律。王建伟等[13]利用室内试验研究了钢弹簧隔振器对浮置板轨道的动力特性。蒋吉清等[14]研究了剪力铰的减振效果及参数优化问题。

但上述研究都是关于浮置板应用于轨道交通方面，而对浮置板应用于市政道路的研究则未见文献报道。本研究以国内首次应用的地下空间上方钢弹簧浮置板减振道路为研究对象，以实测道路振动荷载时程作为车辆荷载激振源，计算了4种车辆和车流荷载作用下有、无浮置板时的地下空间顶板的振动响应，评价了钢弹簧浮置板道路的减振效果。研究成果可为钢弹簧浮置板减振道路的工程应用提供参考。

1 浮置板道路设计方案及评价标准

浮置板道路系统由钢筋混凝土厚板、钢弹簧隔振器、地下空间混凝土顶板及沥青混凝土铺装组成。该系统把混凝土厚板置于可调的钢弹簧隔振器上，沥青混凝土铺装在钢筋混凝土厚板上形成连续路面，最终形成一连续体系的质量-弹簧隔振系统，降低车辆激振导致的地下空间结构的振动和噪声。

研发的钢弹簧浮置板道路系统位于万博中央商务区核心区万惠一路地下空间上方(图1所示)，双向双车道。地下空间为二层地下结构，地下一层为半敞开式地下结构，层高5 m，顶板厚0.8 m，地下二层层高5 m，顶板厚1.2 m，由剪力墙和立柱支撑；混凝土浮置板全长139.5 m，板宽10.0 m，板厚0.45 m，钢弹簧隔振器624个，刚度5.3 kN/mm，间距1.8 m×1.8 m。

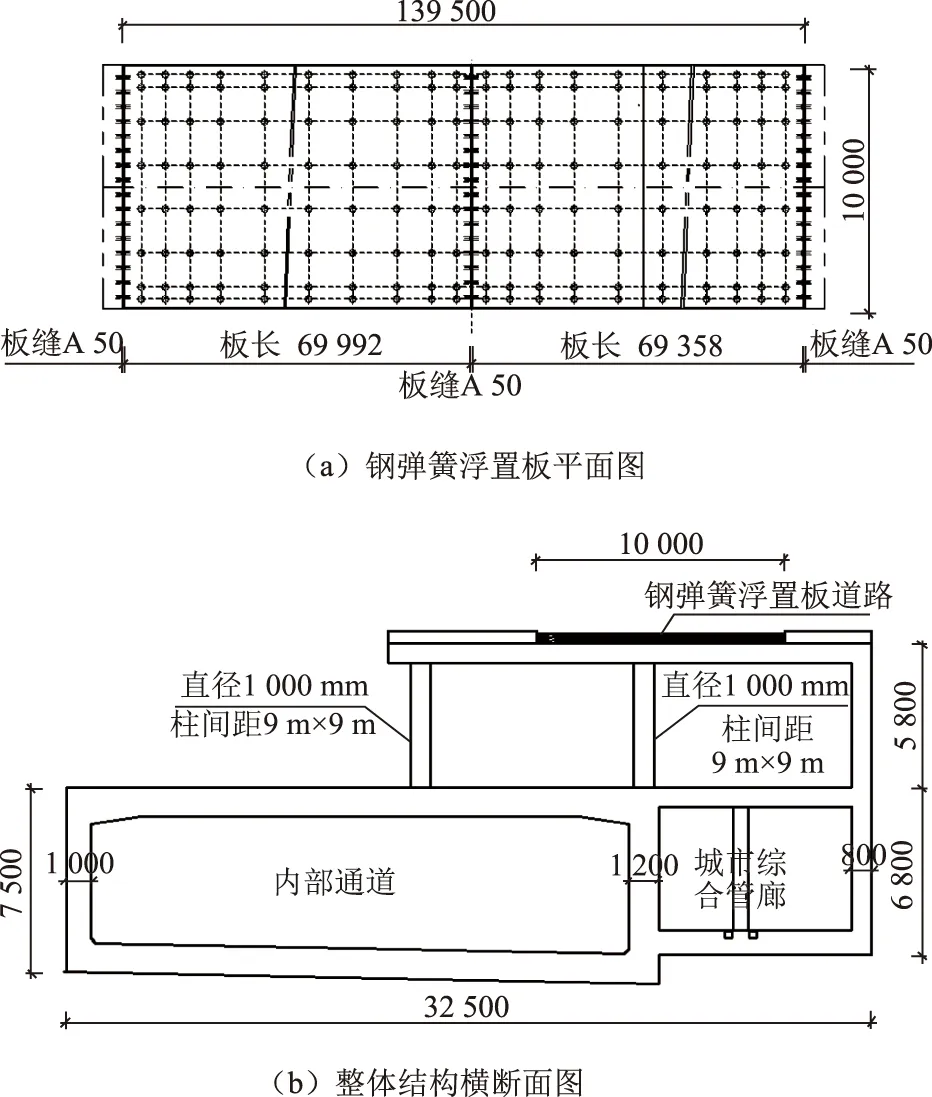
图1 钢弹簧浮置板(单位：mm)Fig.1 Steel spring floating slab (unit:mm)

由于地下商场的顶板直接位于市政道路行车道下，汽车荷载的加-卸载循环引起地下结构尤其是顶板较大幅度的振动和噪音，对商业活动产生较大的负面影响，影响舒适感和健康。另一方面，引起的地下空间结构振动，也可能导致结构损伤、裂纹甚至沉降。根据《城市区域环境振动标准》(GB 10070—88)[15]和《声环境质量标准》(GB 3096—2008)[16]，应按2类振动环境标准，即Z振级昼间和夜间分别不大于75 dB和72 dB，环境噪声等效A声级昼夜间分别不大于60 dB和50 dB。

2 市政道路汽车荷载激振源

2.1 基本原理

古典的车桥振动理论适用于简单系统，对于现实复杂的情况，古典理论无法从理论上给出合理的解释。随着计算机的发展，从古典的车桥振动理论基础上发展完善了现代车桥振动理论，现代车桥振动理论考虑了桥面不平整度对车辆荷载产生的作用，更接近实际情况。

为了获得合理的汽车荷载激振源，需要进行现场实测。根据结构动力学可知，结构在动力荷载作用下产生响应可以分为瞬态响应和稳态响应。由于有阻尼的存在，瞬态响应很快会衰减为零，剩下稳态响应如式(1)所示，而稳态响应频率就是荷载频率。因此，进行现场实测，能够获得车辆荷载产生的真实频率。

y(t)=ρsin(ωt-θ),

(1)

(2)

式中，y为位移;t为某一时刻点;ρ为稳态振动的振幅；ω为汽车荷载频率；θ为振动响应的相位比荷载相位所滞后的角度;α为阻尼比；β为汽车荷载频率与结构固有频率之比。

2.2 测试概况

为了较准确地得到车辆荷载激励频率，在番禺大道北辅路进行了城市交通车辆的4种主要车型(小客车、小货车、大货车、公交车)通行时的路面振动测试，以实测路面振动加速度作为地下空间结构上方浮置板道路的荷载激振数据。

试验采用INV3060S采集仪和941B型拾振器，24位同步采集仪，频率误差小于0.01%，幅值误差小于1%，频率0.17～100 Hz，采样频率512 Hz。

2.3 测点布置及测试结果

在道路外侧行车道边缘布设10个测点，纵向间距1.8m，横向0.7 m，每个测点均为竖向，如图2所示。4号测点在各类车型40 km/h时测试结果如图3～图6所示。

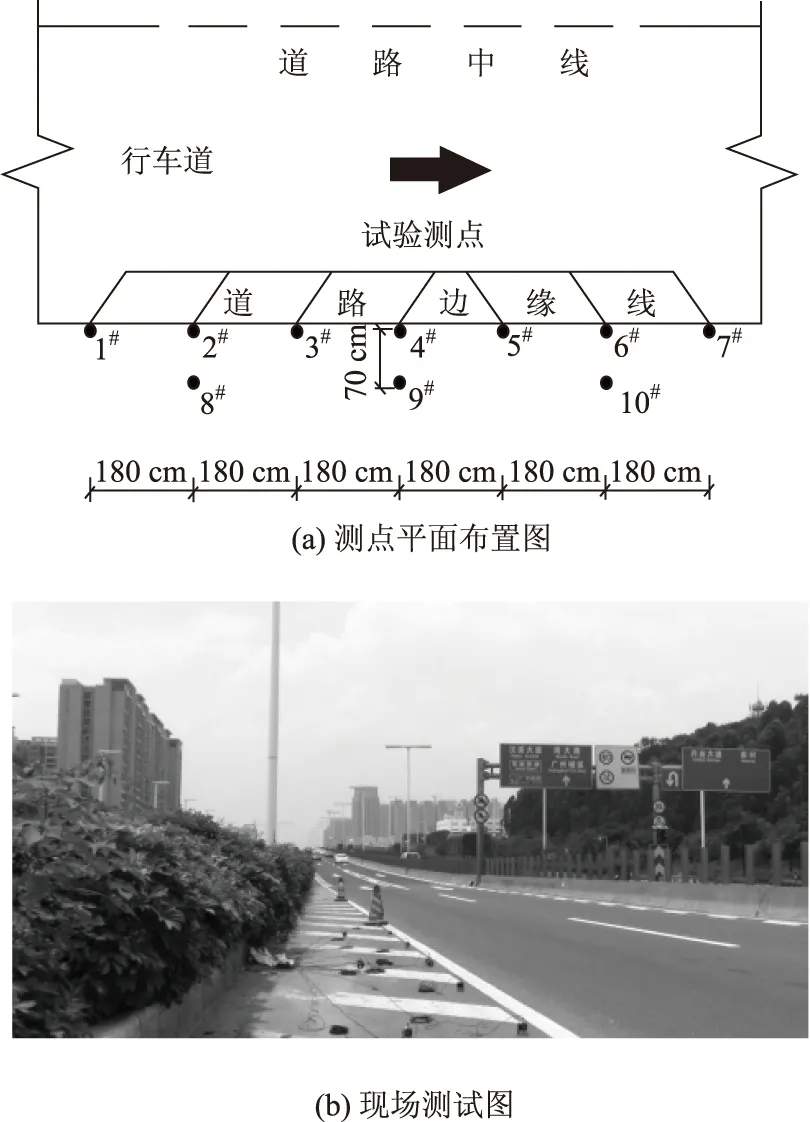
图2 路面振动测点布置图Fig.2 Layout of vibration measuring points on pavement

从图3～图6可以看出，车辆行驶过道路，道路的振动加速度时程响应呈现由弱变强再变弱，且具有明显的周期性，振动能量主要集中在10～40 Hz。由于4种车型的轴重、轴距等不同，因此加速度峰值大小和振动主频不同，小汽车、小货车、大货车、公交车加速度峰值分别为6.6，25.8，33.3，44.1 mm/s2，主频分别在27.5，21.0，16.3，18.0 Hz。

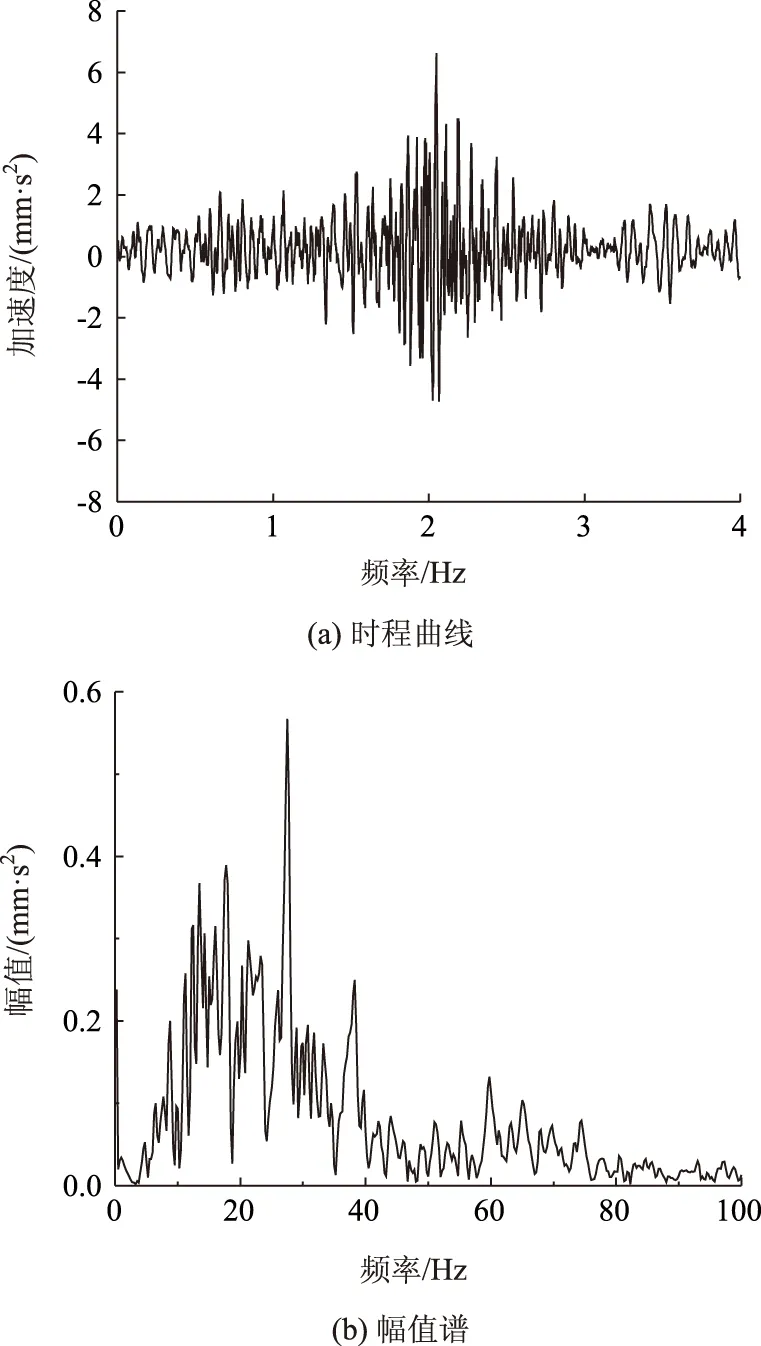
图3 小汽车作用下路面振动时程和频谱Fig.3 Time history and frequency spectrum of pavement vibration under car loads

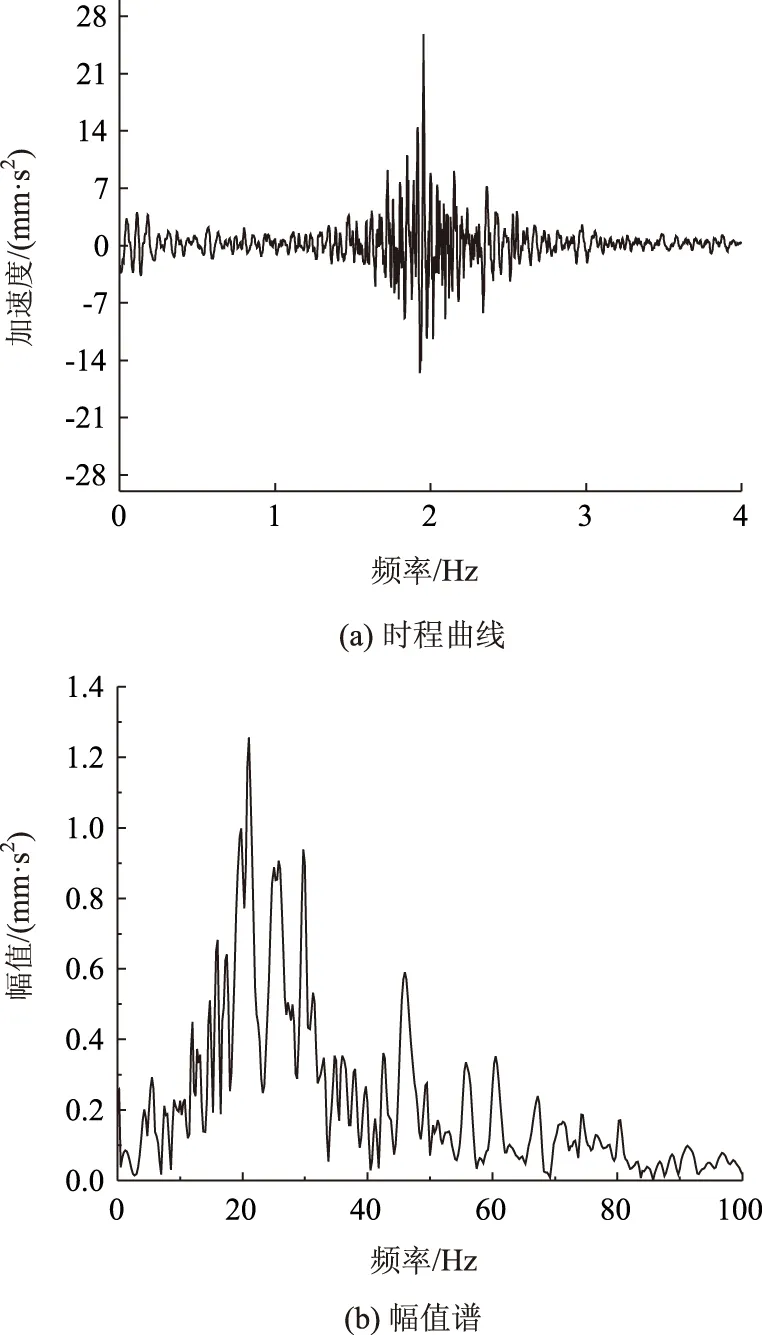
图4 小货车作用下路面振动时程和频谱Fig.4 Time history and frequency spectrum of pavement vibration under minivan loads

图5 大货车作用下路面振动时程和频谱Fig.5 Time history and frequency spectrum of pavement vibration under truck loads

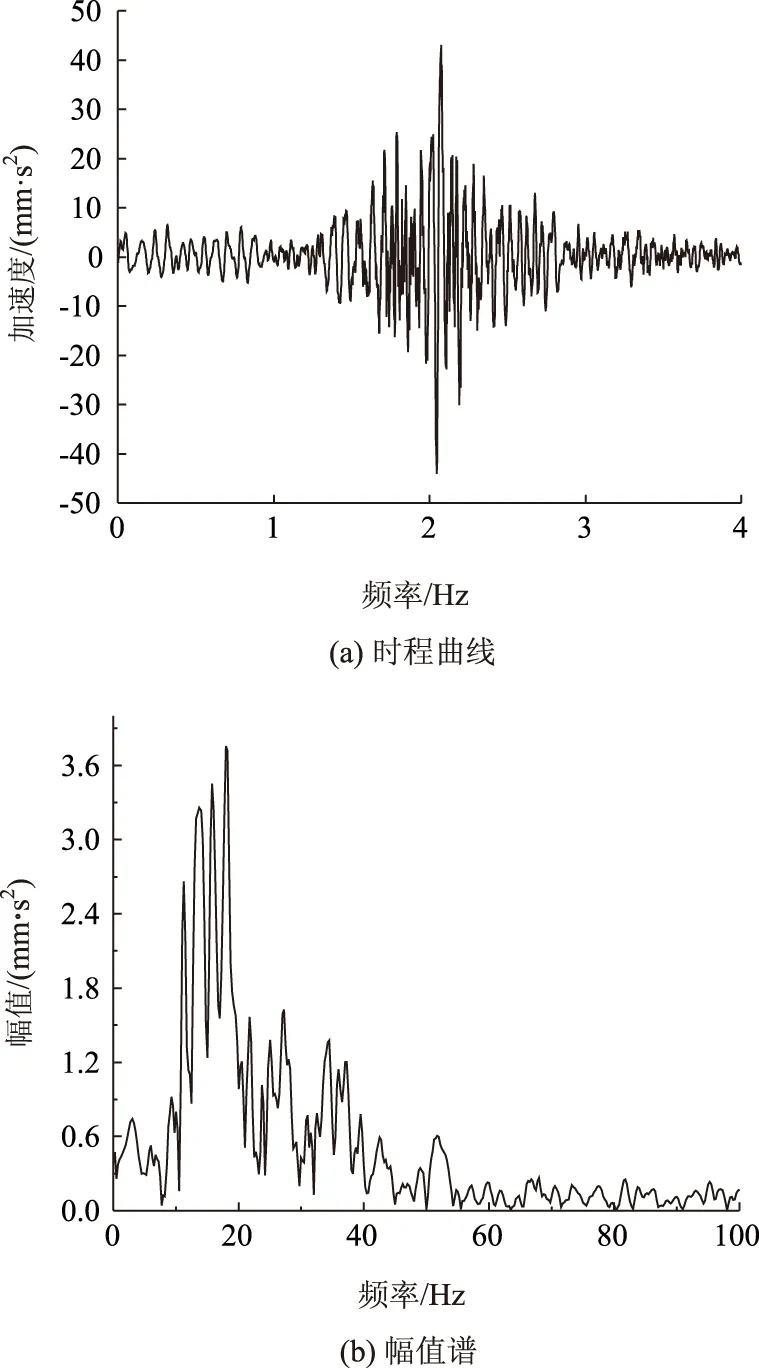
图6 公交车作用下路面振动时程和频谱Fig.6 Time history and frequency spectrum of pavement vibration under bus loads

3 地下空间顶板响应分析

3.1 有限元模型

根据实际工程设计资料，采用大型通用有限元计算软件ansys建立地下空间及其上方浮置板道路整体三维有限元模型，地下结构楼板和侧墙均采用板单元模拟， 立柱用梁单元模拟; 钢弹簧用弹性阻尼连接单元模拟。建立的三维有限元计算模型如图7所示，浮置板地下空间结构的整体模型共7 097节点，7 630单元。

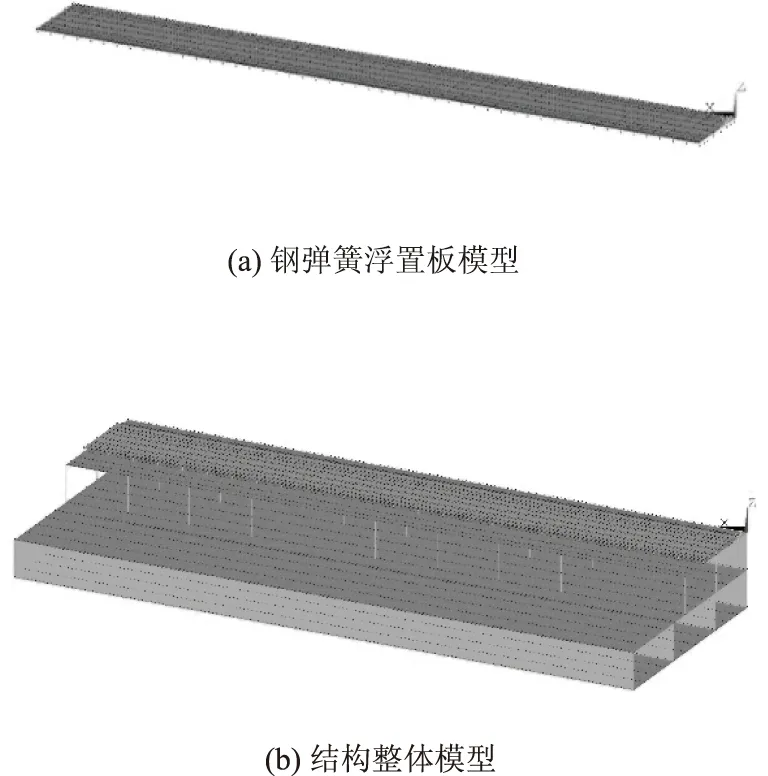
图7 浮置板道路和下部地下空间结构整体三维分析模型Fig.7 Three-dimensional analysis model of floating slab road and underground space structure

3.2 钢弹簧浮置板模态分析

(1)固有频率

根据国内外已有的测试资料和项目测试结果，可知汽车荷载产生的激振能量频段主要集中为10～40 Hz，控制减振效果的关键因素主要是钢弹簧浮置板的是低阶竖向固有振动模态，钢弹簧浮置板、地下空间和设置钢弹簧浮置板后地下空间整体结构前6阶竖向频率如表1所示。

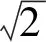
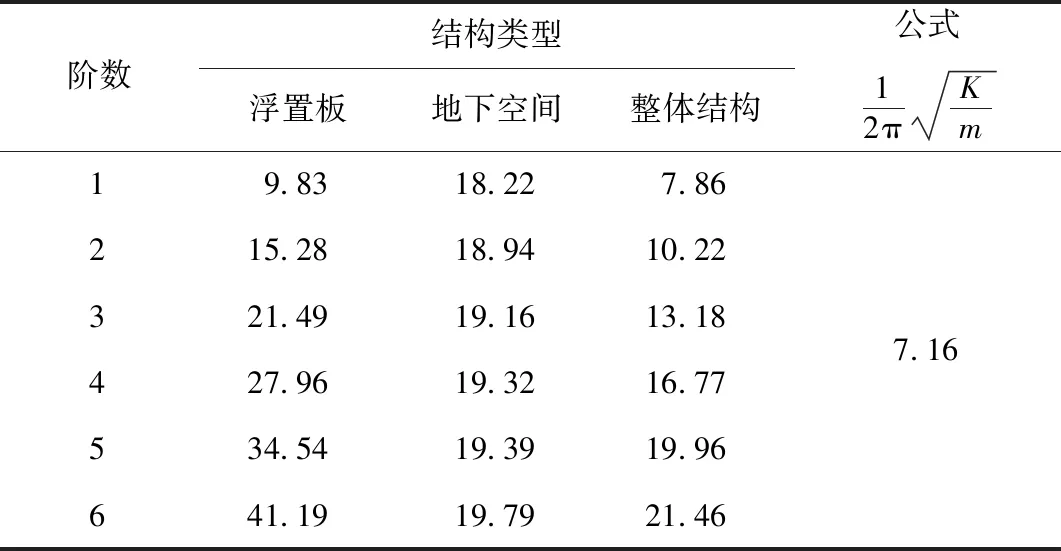
表1 前6阶结构固有频率(单位:Hz)Tab.1 The first 6 orders natural frequencies of structure (unit: Hz)

(2)整体结构振型

振型是结构体系的固有特性，固有频率对应1种振型。图8为浮置板和地下空间整体结构的前6阶振型图。

从图8可看出，前5阶振型主要表现为钢弹簧浮置板的振动，且随着阶数增大而加大；第6阶时表现为地下空间顶板的振动。分析结果表明汽车荷载主要引起地下空间地下一层顶板的振动，未引起结构其余部分的振动。

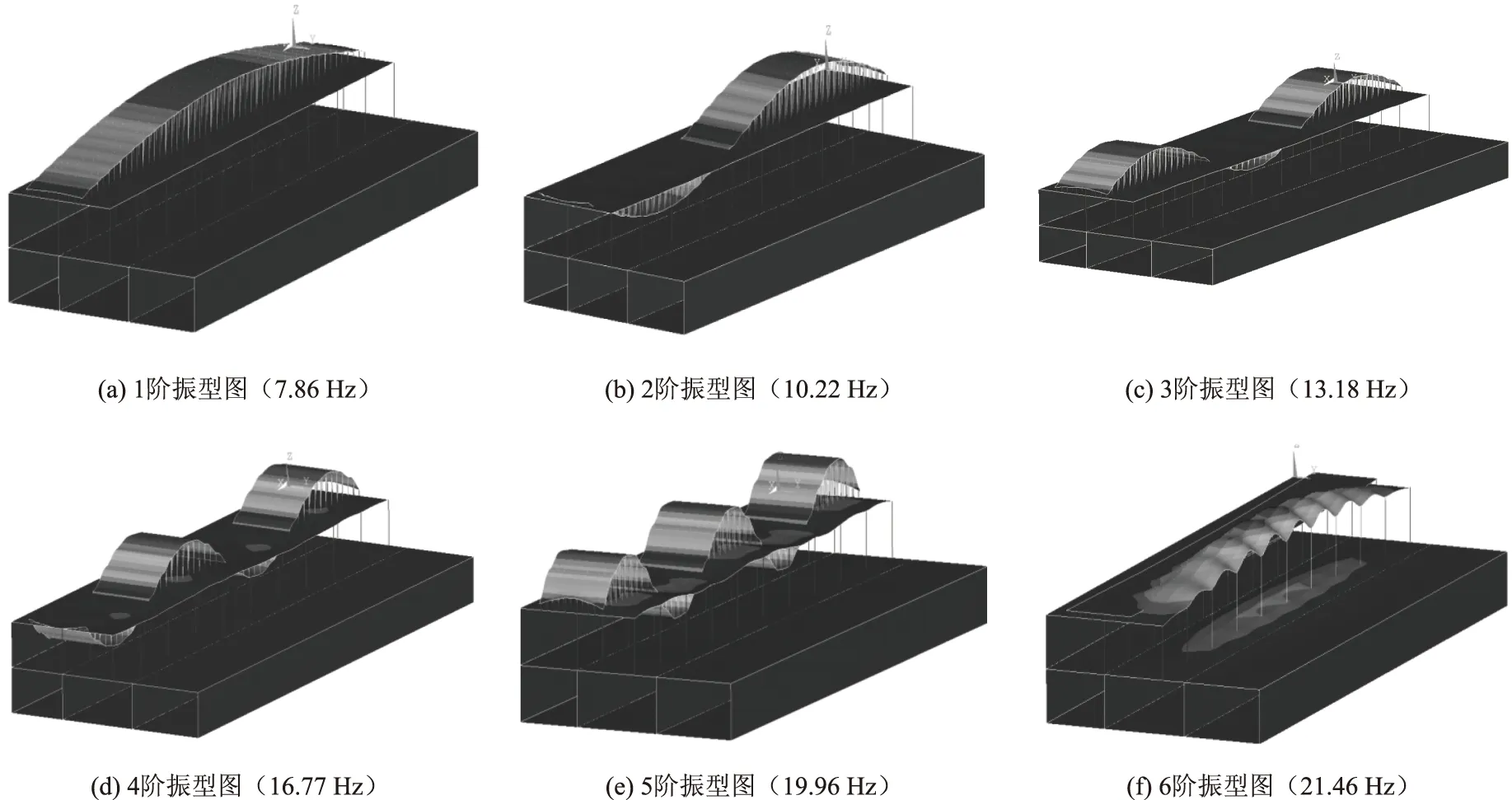
图8 浮置板和地下空间整体结构前六阶振型Fig.8 The first 6 orders vibration modes of floating slab road and underground space structure

3.3 交通荷载激振作用分析

从实测交通荷载激振源的数据中选取小汽车、小货车、大货车和公交车4组数据。采用origin将4组实测数据进行小波降噪。采用DB4小波，阈值类型为sqtwolog，消除白噪声的影响。将降噪后的4组数据归一化，然后乘上(1+冲击系数)再乘上各种车型的重量，结合工程实际，冲击系数取0.1，得到4组计算车型荷载。限于篇幅，选取大货车计算荷载幅值谱如图9所示。将4组计算车型荷载输入ansys有限元模型，进行瞬态动力学计算，结构阻尼采用瑞利阻尼，计算得到了车辆荷载作用下有、无浮置板时地下空间结构的振动响应。

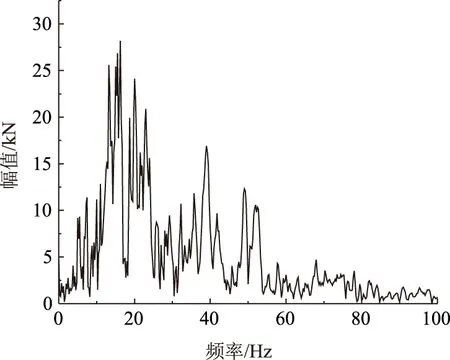
图9 大货车荷载谱Fig.9 Load spectrum of truck

提取地下空间结构中跨的跨中点计算结果作为地下空间结构顶板的代表点。各种车辆作用下钢弹簧浮置板安装前后加速度响应峰值及减振值如表2所示。

从表2可看出，钢弹簧浮置板有明显的减振效果，减振值最低85.8%，最高达90.4%。浮置板是一种性能良好的减振隔振装置，具有将交通荷载相对均匀地重新分配给整个地下空间结构顶板的功能，使顶板从局部受力、振动转化为整体受力、整体微幅振动。

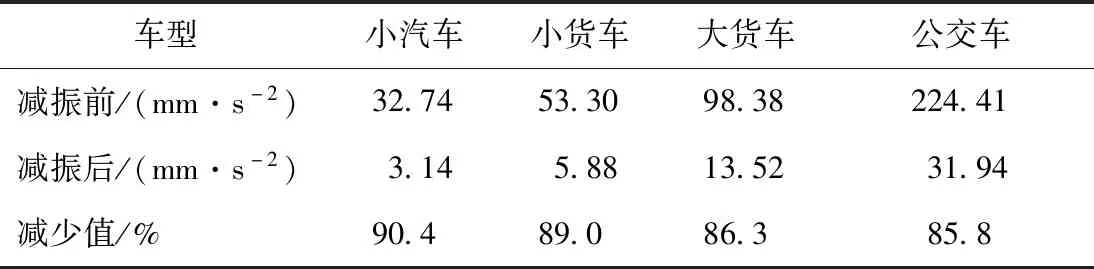
表2 减振前后地下空间顶板加速度峰值Tab.2 Acceleration peaks of underground roof before and after vibration reduction

4 减振降噪效果分析

4.1 振动加速度级评价

根据我国《城市区域环境振动标准》，振动加速度有效值定义为[15]：

(3)

式中，arms为加速度有效值；a(t)为加速度时程；T为加速度持续时间。

振动加速度有效值可作为振动强度指标，但通常采用振动加速度级La代替加速度有效值，即

La=20lg(arms/a0)，

(4)

式中，La为振动加速度级；a为振动加速度有效值;a0为基准加速度，取10-6m/s2。

4种车型的最大加速度级如表3所示，各频段的插入损失如图10所示。

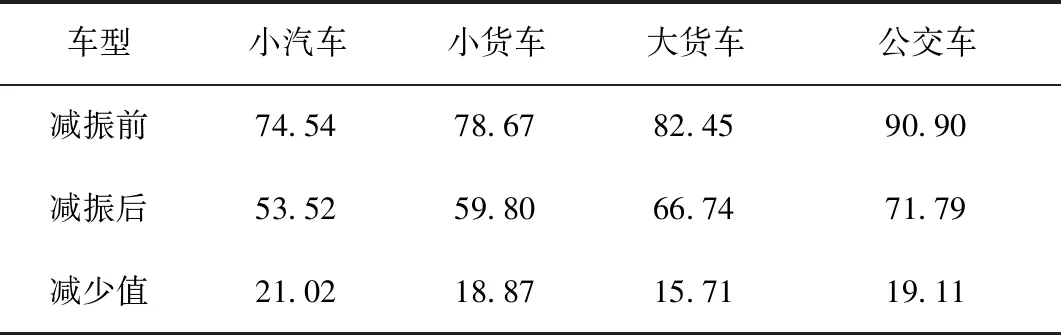
表3 减振前后地下空间顶板最大加速度级(单位:dB)Tab.3 Maximum acceleration levels of underground roof before and after vibration reduction (unit: dB)

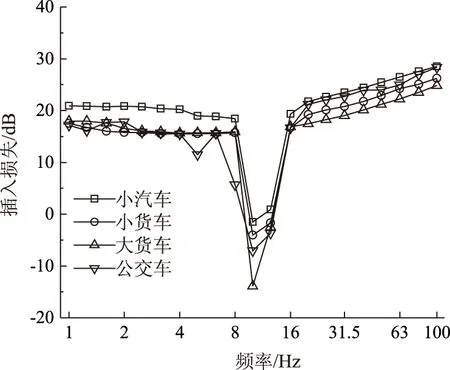
图10 插入损失曲线Fig.10 Insertion loss curves

从以上结果可知，各种车辆作用下的插入损失曲线基本相同，且在大于浮置板基频的频率范围内非常相近。钢弹簧浮置板对振动加速度级的减少值最少15.71 dB，减振效果满足规范要求。

4.2 Z振级评价

Z振级VLz为按ISO 2631/1—1985[17]规定的全身振动Z 计权因子(wk)修正后得到的振动加速度级，公式为[17]：

VLz=20lg(a′rms/a0)，

(5)

(6)

式中,a′rms为振动加速度有效值，a0为基准加速度，取为a0=10-6m/s2；afrms为中心频率f的加速度有效值；cf为Z计权因子。

表4为计算了各类车型的Z振级。从表4可以看出，各种车辆作用下的插入损失基本相同，钢弹簧浮置板对Z振级最小为15.30 dB，结果满足规范要求。

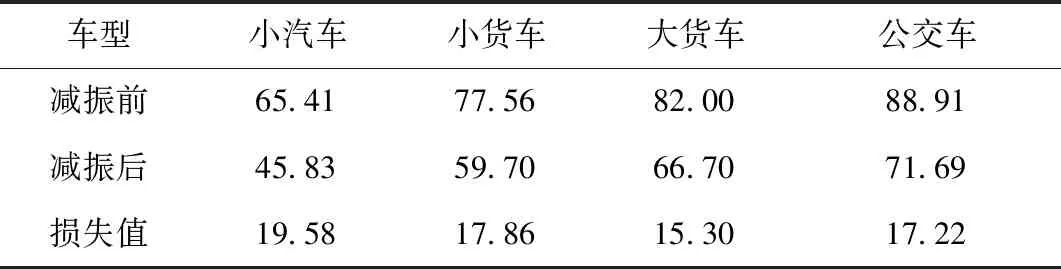
表4 地下空间顶板最大Z振级(单位:dB)Tab.4 Maximum Z vibration levels of underground roof (units: dB)

4.3 二次噪声评价

根据HJ 453—2008《环境影响评价技术导则 城市轨道交通》附录C.2二次结构噪声预测，建筑物内室内中部的二次结构噪声预测计算式为[18]：

(7)

式中,Lp为建筑物内的A计权声压级；Lp,i(f)为未计权的建筑物内的声压级；VLi(f)为与频率相对应的建筑物内的振动加速度级；Cf,i为第i个频带的A计权修正值；f为1/3倍频带中心频率(16～200 Hz)；n为1/3倍频带数。

各类车型作用下A计权的声压级如表5所示。

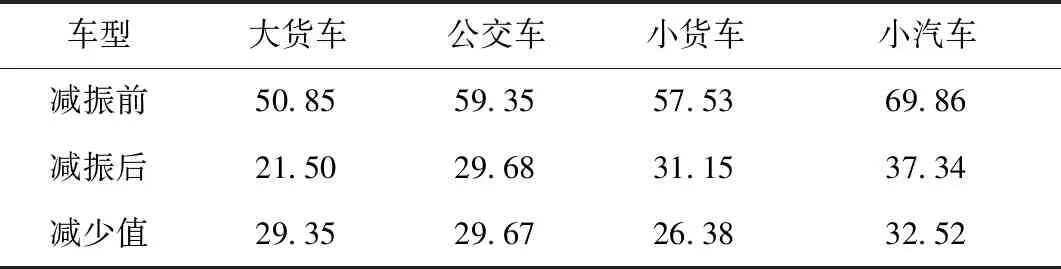
表5 减振前后地下空间顶板最大A声级(单位:dB)Tab.5 Maximum vibration level A of underground space roof before and after vibration reduction (unit: dB)

从表5可以看出，钢弹簧浮置板对二次噪声减少值26.38 dB，降噪效果明显，结果满足规范要求。

5 结论

为研究番禺万博商务中心地下空间上方钢弹簧浮置板示范道路的减振降噪效果，采用现场实测与有限元数值结合方法，分析了实测交通车辆激振源作用下有、无浮置板时地下空间结构顶板的振动响应，进一步采用国家现行标准评价了钢弹簧浮置板的隔振降噪效果。结果表明：

(1)浮置板与地下空间结构合建建筑，低频振动主要为钢弹簧浮置板的振动，钢弹簧浮置板道路能够有效地保证控制地下空间结构振动。

(2)汽车荷载产生的激振能量频段主要集中为10～40 Hz，钢弹簧浮置板应用于市政道路减振时，结构整体设计频率宜低于7.07 Hz。

(3)采用钢弹簧浮置板减振后，各类车型荷载作用下减振效果最低85.8%。钢弹簧浮置板具有将集中荷载重新分配给整个地下空间的功能，使地下空间从局部受力、振动转化为整体受力、整体微幅振动。

(4)采用钢弹簧浮置板减振后，振动加速度级最小减少15.71 dB，Z振级减少15.30 dB，A声压级减少26.38 dB，减振降噪效果明显。