不良地质隧道围岩稳定性预测模型构建与分析
李和元,黄卫国,胡凯
(江西省公路工程监理有限公司,江西 南昌 330100)
监控量测是隧道施工中实时掌握隧道变形的量测手段,如何通过监控量测数据有效预测隧道未知变形是当今研究的热门话题。但该方法只能监测隧道变形实际情况,不能较准确地预测未知的隧道变形规律。灰色模型是隧道施工过程中进行变形预测的有效手段,通过对监控量测实时数据的分析,对未知变形规律进行评估预测。宋海萍对矿区地表沉降灰色系统理论预测模型进行研究,认为将灰色理论应用于矿区地表沉降预测很准确;兰泽全等进行煤矿特别重大事故灰色预测与分析,得出灰色预测有利于实时掌握煤矿地表变形情况,能准确判断未知的变形规律;牛景太等对施工期高心墙堆石坝沉降变形监控模型进行研究,发现利用灰色理论进行变形预测比监控量测能更有效地掌握施工场地变形规律;秦拥军等采用基于灰色关联理论的Peck法进行隧道地表移动参数影响研究,发现灰色模型预测值与实际值的相对误差较小,且精度符合施工要求;刘鹏程等采用分数阶算子灰色理论对隧道围岩变形进行了预测。利用灰色理论建立灰色模型对工程地表变形进行预测可行,且预测精度达到设计与施工要求。该文基于灰色理论建立隧道围岩稳定性预测模型,以某软岩条件下不良地质隧道为例,分析该模型预测值与实际值之间的误差,提出合理的不良地质隧道围岩稳定性预测模型。
1 灰色理论预测模型的构建
1.1 模型构建
隧道变形是以时间线来监测的,故以时间线为依据建立灰色预测模型。对于所得隧道监测变形数据,不需进行相应规律分析和概率统计,仅需对已知数据进行相应处理即可得到与时间序列相关的数据。隧道变形沉降监测时间的序列为:
T(0)={T(0)(1),T(0)(2),T(0)(a-1),
T(0)(a)}
(1)
式(1)中,沉降监测时间序列没有规律,故按式(2)对式(1)中数据作一次累加处理,将数据序列变为有规律序列。
(2)
通过一次累加处理,得到隧道变形沉降监测时间的新序列:
T(1)={T(1)(1),T(1)(2),T(1)(a-1),
T(1)(a)}
(3)
按照同样的方法,得到隧道变形沉降监测值的原始数据序列和新序列:
(4)
根据灰色理论,所得到的新序列服从指数分布,隧道变形沉降监测值F与隧道变形沉降监测时间T之间的一阶线性微分方程为:
(5)
式中:A、B为灰色参数。
对式(5)进行积分求解,得:
F(T)=C·exp(A-AT)+BA-1
(6)
T=1时,有F(T)=F(1),代入式(6),得:
F(1)=C·exp(A-A×1)+BA-1
(7)
解得C=F(1)-BA-1。
隧道变形沉降监测值F与隧道变形沉降监测时间T之间的一阶线性微分方程可表达为:
F(T)=(F(1)-BA-1)·exp(A-AT)+
BA-1
(8)
根据函数在导数上面的定义,可知:
(9)
要使函数能与一次累加的新序列联系上,只需使ΔT→1即可。将ΔT→1代入式(9),得:
(10)
由于一阶线性微分函数是连续的,ΔT较小时,函数值不可能出现较大波动。因此,要得到较合理的隧道变形沉降监测值F,只需取F(T)和F(T+1)的平均值即可。将该平均值代入式(5),得:
F(0)(T+1)=B-0.5A[F(1)(T)+
F(1)(T+1)]
(11)
基于上述推导,当T=1,2,…,a-1,a时,代入式(11),得:
(12)
将式(12)用矩阵方式表达,并进行简化,得:
(13)
令:
式(13)可写为:
F=F*D
根据最小二乘法,得:
(14)
式(14)即为灰色参数的计算式。隧道大变形预测的函数表达式为:
exp{-A[T(1)(i+1)-T(1)(1)]}+BA-1
(15)
式中:i=1,2,…,a-1,a。
1.2 灰色理论预测模型验算
隧道变形沉降监测值F原始数据的平均值为:
隧道变形沉降监测值F原始数据的方差为:
1.2.1 残差验算
由于灰色理论的构建是按照相应序列开展的,残差验算也需要先设定相应样本数据的残差序列ω(0)(i):
残差序列ω(0)(i)的平均值为:
残差序列ω(0)(i)的方差值为:
引入方差比ν和误差概率P:
式中:SF和Sω(0)为隧道变形沉降监测值F原始数据的方差值和残差序列ω(0)(i)的均方差。
方差比ν和误差概率P对于灰色理论预测模型精度的评价标准见表1。

表1 残差对灰色理论预测模型精度的分级标准
1.2.2 关联度验算
通过计算预测值与实测值之间关联性大小判断灰色理论预测模型的精度。假定:
引入关联系数ξ(i),其表达式如下:
ξ(i)=

关联度R是结合方差比ν和误差概率P对灰色理论预测模型精度进行的综合评价,计算公式见式(16),评价标准见表2。

表2 关联度对灰色理论预测模型精度的分级标准
(16)
1.2.3 后验差验算
后验差验算是基于残差验算开展的,其计算方式及等级评价标准与残差验算一样,不再赘述。
2 算例分析
十房(十堰—房县)高速公路通省隧道为分离式隧道,全长6.887 km,采用设计速度80 km/h双向四车道标准建设。该隧道穿越绢云母片岩地层,是国内规模最大的变质软岩隧道,存在软岩大变形、突泥涌水等不良地质。表3为其拱顶沉降监测数据。通过上述灰色理论预测模型预测其拱顶沉降,并与实测值进行对比分析。

表3 通省隧道拱顶沉降监测数据
根据表3,隧道拱顶沉降监测时间序列如下:
F(0)=(F(0)(1),F(0)(2),F(0)(3),F(0)(4),F(0)(5),
F(0)(6))=(134.5,143.0,146.4,150.0,
152.3,155.1)
对F(0)作一次累加,得到新的序列:
F(1)=(F(1)(1),F(1)(2),F(1)(3),F(1)(4),F(1)(5),
F(1)(6))=(134.5,277.5,423.9,573.9,
726.2,881.3)
对序列F(1)作紧邻均值生成,将数据代入式(13),得:
f(1)(i)=(f(1)(2),f(1)(3),f(1)(4),f(1)(5),
f(1)(6))=(206,350.7,498.9,650.05,
803.75)
则有:
将F和F*代入式(14),得:
将计算得到的A和B代入式(5),得:
将上述数据代入式(15),得到隧道变形预测模型如下:
4 581.102 07
(17)
由式(17)可知:
F(1)(5),F(1)(6))=(134.5,279.91,429.8,
584.32,743.60,907.79)
累减生成新序列:
159.28,164.19)
原本的序列为:
F(0)(i)=(134.5,143.0,146.4,150.0,152.3,
155.1)
将上述数据代入公式,得到隧道变形预测结果(见表4),预测结果与实测值的对比见图1。
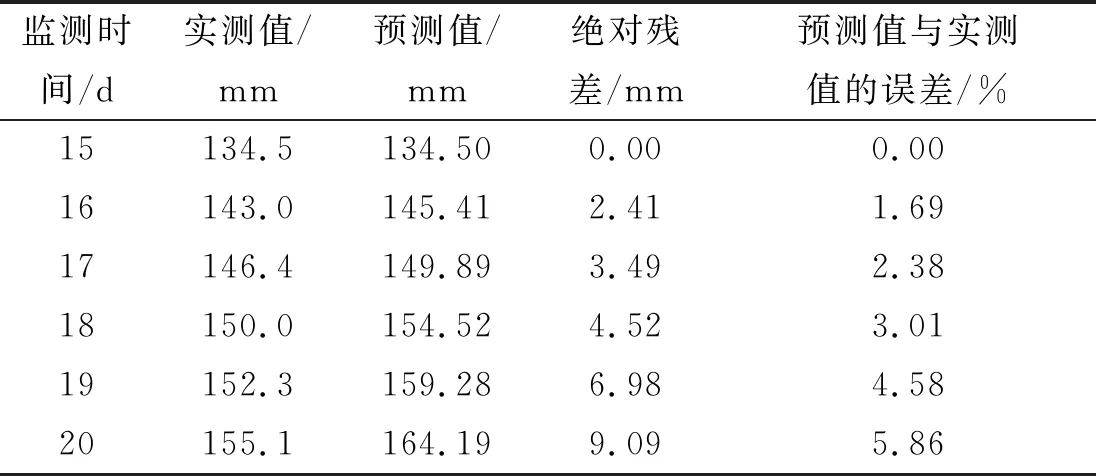
表4 隧道拱顶沉降监测数据与预测数据对比
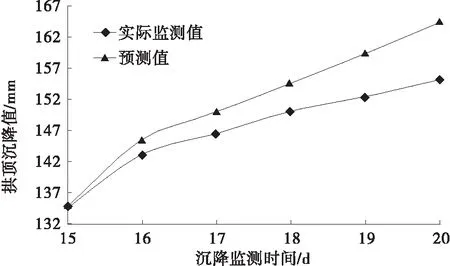
图1 隧道变形预测结果与实测值对比
由表4和图1可知:对15~20 d隧道拱顶变形实测值和预测值的最大误差为5.86%,最小误差为零,模型精度符合要求;随着拱顶沉降监测时间的增加,拱顶沉降预测数据与实测数据间的相对误差虽然在可接受范围内,但误差越来越大。
3 结论
(1)隧道拱顶变形随着时间的增加而增大。灰色预测模型的最大误差为5.86%,最小误差几乎为零,模型精度满足要求。
(2)利用灰色理论构建预测模型,随着隧道拱顶沉降监测时间的增加,拱顶变形预测数据与实测数据的相对误差虽在允许范围内,但误差越来越大。

