基于沉降实测数据的软土地基土工参数优化计算*

刘展瑞，张潭，罗克文，吕琰，易真

(1.广西壮族自治区玉林公路发展中心，广西 玉林 537000；2.长沙理工大学 交通运输工程学院，湖南 长沙 410114)

软土地基具有高压缩性与低承载力的工程特性，在上面修筑公路路堤会出现失稳和不均匀沉降，需对其进行加固处理。针对地基的固结排水过程，陈伟通过数值仿真计算，分析了堤基固结沉降过程及规律，并与现场水库堤基的沉降监测数据对比，预测了堤基沉降达到稳定时所需的固结时间及最终固结沉降值。李强等介绍了双曲线法、星野法、指数曲线法等沉降分析方法，并利用实测沉降数据推算了任意时间的沉降量，预测了软土路基的沉降变形趋势。周舟等结合嘉绍(嘉兴—绍兴)高速公路，分析了软基沉降预测原理，提出了任意地基一维固结问题的解，并利用实际沉降数据对计算模型和参数进行反演，对公路最终沉降及工后沉降进行了预测。彭占淇从软基的孔隙变化规律出发，以大应变固结理论为基础建立适合软土的三维固结模型，运用有限差分法构造显示差分格式，并利用MATLAB软件编程进行求解。谢康和对双层地基一维固结特性进行分析，对荷载在时间任意变化及起始孔压沿深度任意分布的情况下双层地基一维固结进行了解答。但对基于现场沉降数据反算土工参数的研究没有涉及。该文以广西玉林市博白县省道S209线路面大修工程软基为原型施加荷载，使大部分沉降在预压过程中完成，通过现场实测沉降数据计算得到各土层的土工参数。

1 多层软土地基固结排水过程的理论推导

令cvi为成层土层的竖向固结系数，ui为时空状态(成层土层i中任意一点任意时刻)下超静孔压力，H为n层地基总厚度，hi为第i层成层土厚度，mvi为土层i的体积压缩系数，kvi为土层i的渗透系数，Esi为土层i的压缩模量。其他参数定义如下：

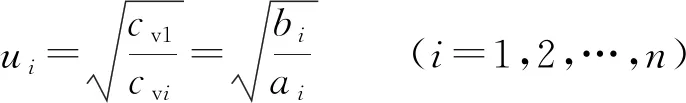
根据太沙基经典一维固结理论中超静孔压解的形式，ui可由下式表示：

(i=1,2,…,n)

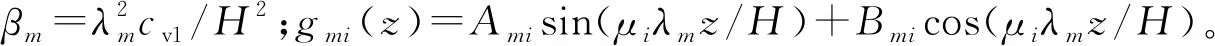
土层i的平均固结度为：

地基平均固结度为：

由于上述求解过程已求得任意成层土层i的平均固结度Ui，通过按沉降定义的地基平均固结度的计算公式即可计算出软土地基的地基平均固结度。

2 多层软土地基的软化模型问题

基于现场实测数据，先通过最小二乘法推导成层地基在变荷载下任意层任意时刻的固结系数，即时空状态下固结系数。太沙基经典一维固结理论虽被广泛应用于工程建设项目中，但其假设与工程实际有很大差别，它将任何地基都视为一层，其计算结果可能与实际有所偏差。故在讨论多层软土地基固结排水过程时，考虑与固结系数关系非常大的时间及空间因素，推导出多层软土地基的固结排水过程，计算任意时间点及成层地基的固结系数，该时空状态下的固结系数能更好地为工程建设提供帮助。

玉林市公路片石处理为2层地基。针对双层软土地基，根据文献[7]可得到a1、a2、b1、b2、cv1、cv26个主要土工参数满足下式：

(j=1,2,…,ε)

即:

(1)

式中：Uij按式(2)计算。

(2)

式中：Cm按式(3)计算。

(3)

令：

(4)

令x=(x1,…,xn,xn+1,…,x2n,x2n+1,…,x3n)=(a1,…,an,b1,…,bn,cv1,…,cvn)，得：

(j=1,2,…,ε)

(5)

式(4)可转化为：

(6)

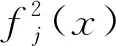
φj(x)=fj(xk)+∇fj(xk)(x-xk)=

∇fj(xk)T8x-[∇fj(xk)Txk-fj(xk)]

(j=1,2,…,ε)

(7)

式(7)中右端为上述函数xk+1在xk点展开的一阶泰勒多项式。令：

(8)

以式(8)中φ(x)近似替代F(x)，将φ(x)的极小值作为目标函数F(x)极小值的估计值，得：

φ(x)=(Ax-B)T(Ax-B)=

xTATAx-2BTAx+BTB

(9)

式中：A、B分别见式(10)、式(11)。

(10)

(11)

令：

∇F(x)=∇φ(x)=2ATAx-2ATB=0

(12)

求出φ(x)的平稳点，将A、B代入式(12)，得到ATAx=AT(Axk-f(k))，进而得：

ATA(x-xk)=-ATf(k)

(13)

式中：f(k)接式(14)计算。

(14)

ATA为对称正定矩阵，即A为满秩时，存在逆矩阵(ATA)-1，可通过式(8)得到φ(x)的稳定点：

xk+1=xk-(ATA)-1ATf(k)

(15)

3 实际工程应用

对玉林市某公路双层软土地基固结排水过程进行分析，利用基于工程现场实测沉降数据获取的双层软土地基土工参数及模型对软基沉降进行计算，为该公路软基沉降量分析提供理论依据。

取玉林市某公路K28+280、K46+800断面进行计算。两断面均为双层地基，断面K28+280的层高分别为5.4、8.4 m，断面K46+800的层高分别为4.6、12.7 m。通过实际测量，得到各断面的时间-沉降-固结度(见表1)，各断面不同时间点各土层的固结度见图1，各土层的相关土工参数ai、bi、cvi计算结果见图2。

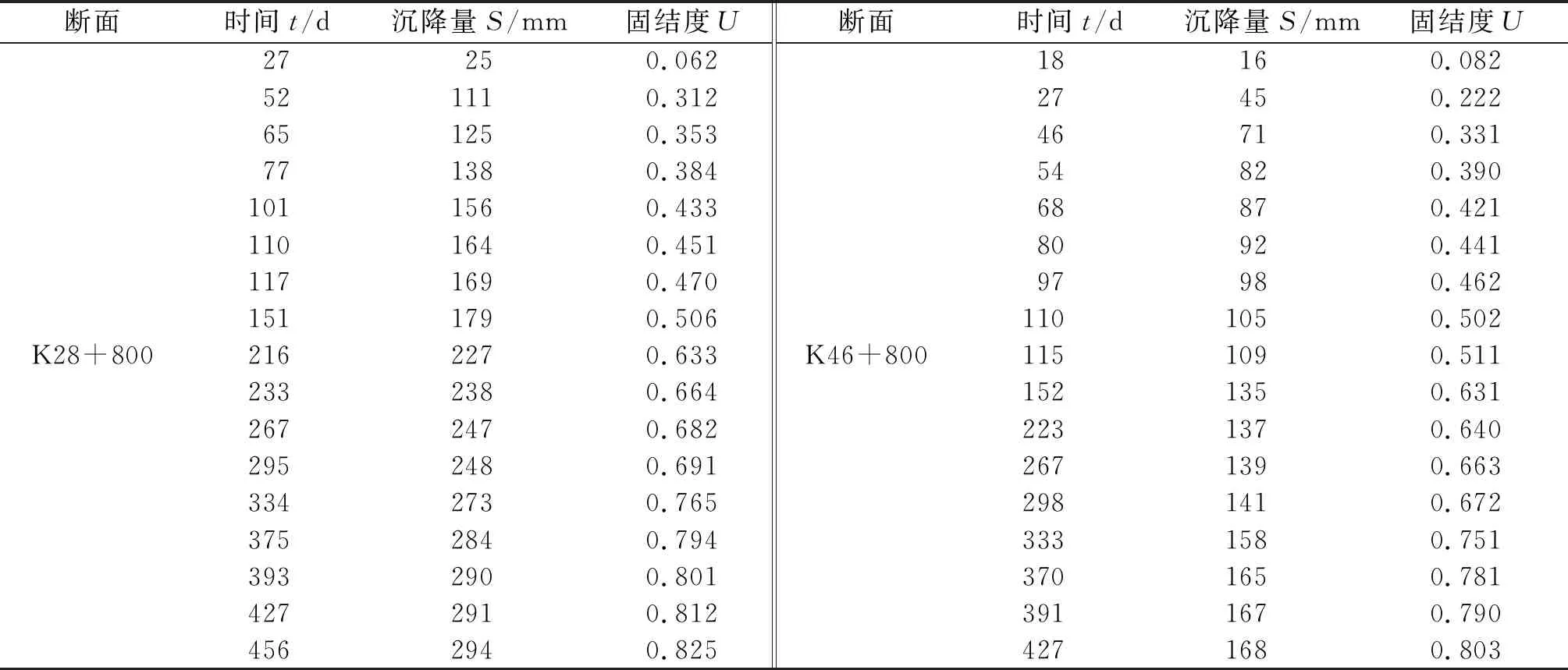
表1 两断面的时间-沉降-固结度

图1 各断面不同时间点各土层的固结度变化

图2 两断面各土层土工参数计算结果

从表1可看出：K28+280、K46+800断面的沉降量和固结度随着时间的增加而增大。

从图1可看出：2个断面不同时间点各土层的固结度都逐渐增大，第一层地基的固结度大于第二层地基的固结度，但其固结度变化幅度逐渐变小，曲线逐渐平缓，并趋于某一范围值。

从图2可看出：2个断面软土地基的第一层土工参数逐渐增大，成层土层的竖向固结系数逐渐增大；第二层土工参数逐渐减小，土层的竖向固结系数逐渐减小；两者的变化幅度都逐渐减小并趋于一个稳定范围值。

基于软土地基实测沉降数据计算地基土工参数，其精度较高，且收敛速度较快，可减少因误差带来的影响，将沉降量控制在工后沉降范围内，能应用于公路建设项目中。

4 结语

将理论与玉林软基公路相结合，建立基于现场实测沉降数据获取软土地基土工参数的优化模型，将工程现场实测数据与加载值输入模型即可得到固结系数及土工参数。计算结果显示，不同断面各土层不同时间点的固结度逐渐增长，并慢慢趋近于某一范围值。该方法可避免室内实验的难点，且通过现场实测数据计算出的土工参数比实验室内得到的土工参数更准确，避免了土样在运输、制作及实验过程中发生变化造成结果不准确的困扰。