优化的代价敏感随机森林算法设计研究
任宇轩


摘要:代价敏感随机森林算法是解决不平衡数据分析的一种典型方法,在许多领域应用广泛,但其存在着两个不足一是构造代价函数时未考虑样本分布情况,二是对于数据集内的所有特征其距离计算过程相同,未突出重要特征。为解决上述问题,本文提出了一种优化方法根据样本分布情况构造代价因子,并引入权重距离,以提升算法性能。
关键词:随机森林;代价敏感;不平衡数据
1代价敏感学习
在处理不平衡数据时,由于多数类样本与少数类样本数量相差巨大,会导致学习结果出现偏差,生成的分类器会完全偏向于多数类。如样本空间为1000的数据集,为二分类,其中多数类样本995个,少数类样本5个,那么分类器在对待新样本时,只需要将其机械的分为多数类,其准确率也在99.5%左右。而这种分类方法却远不同于我们的需求,往往我们希望分类器能够更加准确的分出少数类。如医院在诊断癌症患病者时、银行在判断贷款有无坏账风险时等。
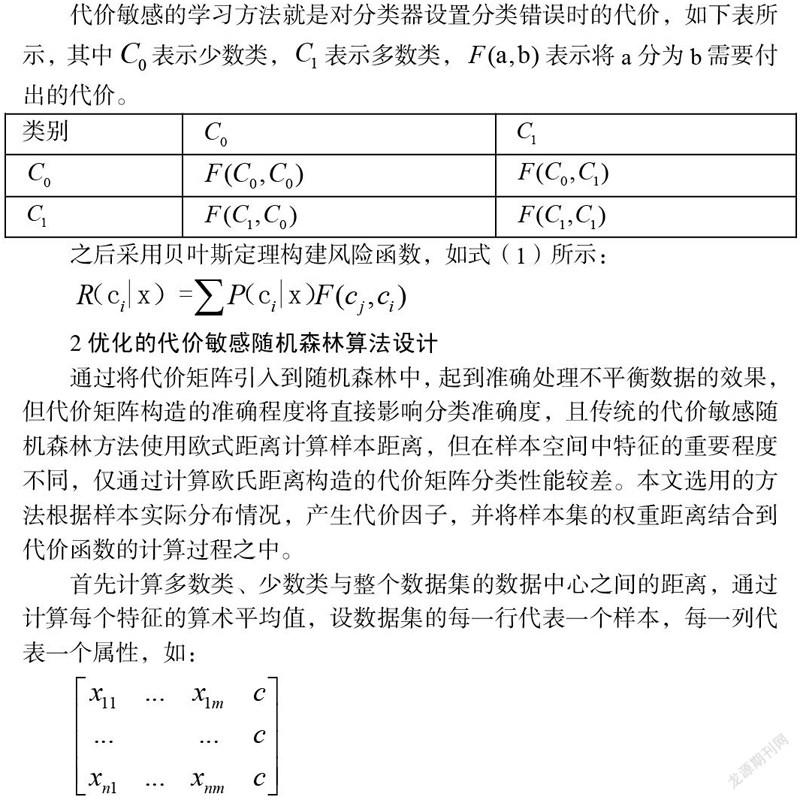
代价敏感的学习方法就是对分类器设置分类错误时的代价,如下表所示,其中表示少数类,表示多数类,表示将a分为b需要付出的代价。
之后采用贝叶斯定理构建风险函数,如式(1)所示:
2优化的代价敏感随机森林算法设计
通过将代价矩阵引入到随机森林中,起到准确处理不平衡数据的效果,但代价矩阵构造的准确程度将直接影响分类准确度,且传统的代价敏感随机森林方法使用欧式距离计算样本距离,但在样本空间中特征的重要程度不同,仅通过计算欧氏距离构造的代价矩阵分类性能较差。本文选用的方法根据样本实际分布情况,产生代价因子,并将样本集的权重距离结合到代价函数的计算过程之中。
首先计算多数类、少数类与整个数据集的数据中心之间的距离,通过计算每个特征的算术平均值,设数据集的每一行代表一个样本,每一列代表一个属性,如:
然后需要计算各类样本中心到数据集中心的权重距离,在数据集中,重要特征相对较少,计算类别中心到整个数据集中心的欧式距离构造代价对重要特征不公平,本算法引入权重距离,利用信息增益衡量每个特征在不同类别中的重要性,如下式所示
第三步,设多数类,少数类,其中样本数分别为,能够定义系数如下:
最后,设d表示权重距离,可得到代价函数如下:
算法基分类器组合阶段,针对不平衡数据,每棵决策树使用 AUC 值进行性能的在评估,利用 AUC 值对数据进行加权投票,权重越大,说明该基分类器性能较好,在最后决策阶段占的权重越大,对于分类性能差的,权重越小,对结果的影响就小。最后随机森林分类器的输出为
3实验与分析
为验证方法准确性,本文选取公开数据集UCI中的多组数据将其转化调整为两类不平衡数据,对决策树(C4.5)、随机森林分类器(RF)、传统代价敏感随机森林与选用的的优化的代价敏感随机森林算法进行对比。
其中C4.5分类器算法比较直观,实现简单,但是容易对数据造成过拟合,特别当特征较多时,训练的决策树较复杂,且没有考虑不平衡数据的特点,少数类性能很差。 随机森林分类器的性能优于传统决策树算法,但其同样没有对不平衡数据集针对学习,对少数类样本的分类结果较差。而引入代价敏感的两种算法可以较好地处理不平衡数据,在AUC性能上有了较大的提高,但是代价敏感的随机森林算法忽略了不同代价类型在分类过程中的重要性,而优化算法能够将不同分类能力的基分类器以 AUC 值赋予权重,有效避免了噪声数据的干扰。实验结果表明,重新构造代价函数、利用 AUC 值对树进行评价,对性能不同的树区别对待对不平衡数据分类是有效的。
从上表中可以看出,虽然优化算法需要稍高的运算资源,且多数类精度有所下降,但其少数类精度提升明显,符合我们设计分类器的需求。
4结语
不平衡数据集给数据分析工作带来了较大的难处,本文选用的优化的代价敏感随机森林方法,能够有效防止分类器盲目将新样本归为多数类,设计了更加合理的代价函数与结果生成方法,通过实验证明,该方法对于处理不平衡数据具有一定的意义。
参考文献
[1]向鸿鑫,杨云.不平衡数据挖掘方法综述[J].计算机工程与应用,2019,55(04):1-16.
[2]陈斌. SMOTE不平衡数据过采样算法的改进与应用[D].广西大学,2015.
[3]马骊. 随机森林算法的优化改进研究[D].暨南大学,2016.
[4]陈圣灵,沈思淇,李東升.基于样本权重更新的不平衡数据集成学习方法[J].计算机科学,2018,45(07):31-37.

