引发山洪的降水特征及动态阈值研究

狄靖月,许凤雯,包红军,徐成鹏,张国平

(1.国家气象中心,北京 100081;2.中国气象局-河海大学水文气象研究联合实验室,北京 100081；3.中国气象局公共气象服务中心,北京 100081)

引 言

我国山洪灾害呈多发、易发、频发、重发的特点。国内有关山洪预警的研究主要集中在数理统计法和历史灾害分析法方面，如陈桂亚和袁雅鸣(2006)、王仁乔等(2006)、孟玉婧等(2019)采用“统计归纳法”对区域临界雨量进行研究；张玉龙等(2007)用内插法推求无资料地区的临界雨量；叶勇等(2008)、樊建勇等(2012)用流量反推法估算山洪临界雨量；张世才等(2007)对几种山洪预警方法进行了比较分析，认为产流分析法确定临界雨量较为合理；曲晓波等(2010)、张亚萍等(2013)从气象成因角度对典型山洪过程进行了分析；彭涛等(2010)、崔春光等(2010)、包红军等(2017)利用定量降水预报和雷达定量降水估算与水文模型相耦合，进行了中小河流洪水预报试验。然而，临界雨量统计归纳法得出的临界雨量很可能并非“真正的”临界雨量，而且大多没有定量考虑前期雨量影响，多以定性为主。由于山洪流量大小除了与降雨量和降雨强度有关外，还与流域下垫面土壤含水量条件密切相关，因此不同场次、不同时间的山洪灾害发生时临界雨量预警阈值是非静态，而是实时变化的。叶金印等(2014，2016)以新安江模型为基础,提出了考虑土壤含水量饱和度的动态临界雨量山洪预警方法。该方法采用新安江模型计算流域的土壤含水量饱和度,根据土壤含水量饱和度以及山洪发生前6 h、12 h和24 h等3个时间尺度的最大降雨量，分别建立3个时间尺度的山洪预警动态临界雨量判别函数；陈瑜彬等(2015)基于流域降雨径流关系，结合流域土壤含水量和前期实测降雨量，计算了河道洪峰流量达到安全泄量所需的下一时段降雨量(临界雨量),并以最小二乘法准则拟合前期实测降雨与临界雨量之间的函数关系，建立了不同土壤含水量等级下的动态临界雨量计算函数；张连成等(2020)利用淹没模型进行了致灾阈值的分析；刘志雨等(2010)将所有场次洪水前24 h的时段最大雨量及其对应的土壤饱和度组成状态空间，给出一条判别曲线，根据对应洪水流量是否超警戒，将状态空间分为两部分，这条曲线就是该时段的动态临界雨量线。国外在这方面最具代表性的方法是由美国水文研究中心较早提出的FFG(Flash Flood Guid⁃ance)方 法(Hapuarachchi et al.，2011；Norbiato et al.，2009)，实际上就是临界雨量，并用该方法与分布式水文模型结合，但存在所拟定临界雨量精度差异大和输入资料要求高等不足。

一直以来，国内相关业务和研究部门对洪水暴雨的研究主要集中在人口密集区域，在理论和方法上多以不同时段的流域洪水过程为研究对象，对超过警戒流域的洪水进行统计分析，进而对山洪的降水阈值进行计算，而非真正基于山洪灾害。如何通过考虑下垫面土壤含水量情况计算真正产生山洪灾害的过程的动态雨量阈值是本文的难点，也是山洪灾害预警技术的关键环节。本文在前面研究的基础上，以实际山洪灾害而非流域水文站流量超警戒水位为研究对象，分析灾害及对应的降水特征，并对引发灾害的不同时效的动态预警雨量阈值影响因子进行分析，建立不同时效的引发山洪灾害的降水动态阈值判别方法，以期在国家级山洪灾害气象风险预警业务中提供技术支持。

1 资料与方法

本文选取全国山洪灾害易发区，并以典型区域(云、贵、川、渝)为例进行研究。使用的山洪灾害灾情信息由中国水利水电科学研究院提供，2013—2016年山洪灾害信息共计370条(包含灾害发生时间、经纬度、灾害类型、灾害等级、失踪死亡人数等)。降水实况资料来源于国家气象中心区域自动站的小时降水资料，统计的自动站有53 652个。土壤含水量(土壤重量含水率、土壤相对湿度)数据取自国家气象信息中心10～50 cm分层土壤含水量信息。

在某时间尺度内，受降雨影响，山区流域流量突增到一定量级，引发山洪灾害，对应时间尺度内的降雨量即为临界雨量，临界雨量对山洪灾害的发生具有至关重要的作用。本文通过分析灾害降雨时空分布特征、不同时段降水量级的频次分布，确定灾害的静态降水临界阈值，并在静态阈值分析的基础上，提取土壤湿度因子，土壤重量含水率及土壤相对湿度等信息，开展降水与不同土壤含水条件的研究。将多次山洪灾害前1 h、6 h、12 h和24 h的实测雨量及其对应的土壤含水量组成状态空间，给出一条外包曲线，使得大部分的灾害点符合该外包曲线，这条曲线就是该时段的动态临界雨量线。通过外包曲线，建立基于土壤含水量的计算方程，该方程可基于当前的土壤湿度信息及未来时段降雨量信息，预报山洪灾害是否可能发生。

2 山洪灾害及降水特征分析

2.1 山洪灾害总体灾情特征

山洪灾害分级标准参考《地质灾害防治条例》(中华人民共和国国务院令(第394号))第四条地质灾害灾情分级规定，死亡失踪人员大于30人(含30人)为特大型，[10，30)人为大型，[3，10)人为中型(含3人)，小于3人为小型(涂勇，2014)。2013—2016年全国共搜集山洪灾情370条(图1)，其中特大型2起，大型12起，中型88起，小型267起，灾害点主要分布在西南、东南、西北地区东部、华北等地。其中，分布密度最大的是西南地区150起，以云南、贵州、四川、重庆等省市分布最广，云南发生次数最多为52次，其次是贵州35次，四川33次，广东33次，重庆28次；其次是东南地区123起，北方地区97起。

图1 2013—2016年山洪灾害点各省(区、市)发生次数分布Fig.1 Distribution of flash flood disasters in each province from 2013 to 2016.

70次灾害中，2013年120次、2014年85次、2015年75次、2016年90次，2013年发生次数最多，2015年次数最少。其中5—9月是山洪灾害高发期，尤其是6—8月，山洪灾害以爆发式增长，其中7月发生山洪次数最多129次，分别发生在7月上旬39次，7月中旬55次，7月下旬35次(图2)。

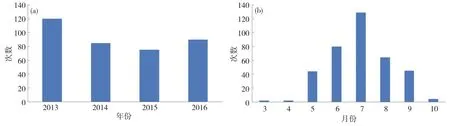
图2 2013—2016年全国山洪灾害时间分布：年分布(a);月分布(b)Fig.2 Temporal distribution of flash flood disasters in China from 2013 to 2016:(a)annual distribution,(b)monthly distribution.

2.2 山洪灾害降水特征分析

暴雨型山洪的特点是突发性强、洪水集中、破坏性强，与降水有着较快的响应关系。由于山洪灾害发生的持续性及多发性，本研究搜集到的山洪灾害并未精确到小时，因此统计山洪灾害前的降水是以灾害发生当日00—24时的时间段作为灾害发生前24 h的降水，灾害发生前一日00—24时的时间段作为灾害发生前24—48 h的降水，以此类推。基于全国53 652个气象加密观测站降水信息，以最近距离判别法，对山洪灾害发生点前24 h、24—48 h、48—72 h累计降水分别进行插值分析，若有重复在同一经纬度发生的山洪灾害点，则选取降水量较大的点的数据进行插值。从2013—2016年山洪灾害发生前两日的降雨情况看(图3)，前24—48 h整体降水小于前24 h降水，即更多的灾害对应着前24 h内的强降水，即使部分地区前24—48 h降水更强，前24 h内也持续着强降雨。当东南地区前24 h降雨达到100 mm以上时易发生山洪灾害，北方和西南部分地区前24 h降雨达到25～50 mm就达到易发山洪灾害的临界点，局部地区甚至达到10 mm以上就需要引起关注。由此可见山洪灾害强降水主要出现在灾害前24 h内，但有少部分是由于持续性的降雨引发。

图3 2013—2016年山洪灾害前24 h(a)、24—48 h(b)和48—72 h(c)降雨分布Fig.3 Precipitation distribution during(a)24 h,(b)24—48 h,and(c)48—72 h before flash flood.

小时雨强也是致灾的一大因素。根据2013—2016年全国山洪灾害前48 h和24 h最大小时雨强分布(图4)可见，前48 h以内出现的最大雨强与前24 h以内出现的最大雨强，大体一致，根据灾害前48 h及24 h内的最大雨强统计分析，前48 h内出现的最大雨强中近77%是出现在灾害前0—24 h内的，23%出现在前24—48 h内。同样可见山洪灾害强降水主要出现在前24 h内，而仍有少部分是由于持续性的降雨引发。因此，灾害前48 h以内的持续性的降水，尤其是24 h、12 h、6 h、1 h内的强降水与引发山洪灾害最为密切相关。

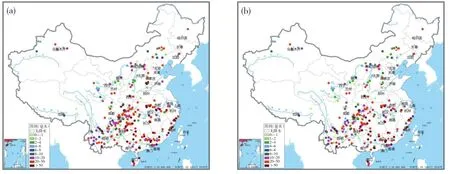
图4 2013—2016年全国山洪灾害前48 h(a)和24 h(b)内最大小时雨强分布Fig.4 Maximum rain intensity distribution during(a)48 h and(b)24 h before flash flood.

根据上文分析，24 h内的短时强降雨是引发山洪灾害的最大因素，由于地理位置差异，引发灾害的降雨阈值与灾害发生关系差异较大，因此，分别对西南地区、东南地区以及北方地区的灾害降雨阈值进行分区研究。对于引发山洪的短时强降雨，由于灾害的突发性，山洪灾害的具体发生时次较难统计，因此本文根据灾害发生的实际时间范围，推求该时间范围前发生的最大过程雨量，作为引发该灾害的实测降水。根据2013—2016年山洪灾害前不同时段降水平均值分布(表1)，西南地区山洪灾害发生前的12 h降雨量平均值为56.2 mm，6 h的降雨量平均值为44.2 mm，3 h的降雨量平均值为34.5 mm，1 h降雨量平均值为19.9 mm；对于东南地区，各时效对应的降雨明显增大，12 h降雨量平均值达到112.1 mm，6 h降雨量平均值为87.5 mm，3 h降雨量平均值为66.7 mm，1 h降雨量平均值为37.4 mm；对北方地区而言，由于样本稀少，且强降雨整体是要小于南方地区，从搜集样本上看，12 h的降雨量平均值达到37.5 mm，6 h的降雨量平均值达到29.2 mm，3 h的降雨量平均值达到21.9 mm，1 h的降雨量平均值达到14 mm，灾害就易发生。

表1 2013—2016年山洪灾害前不同区域不同时段降水平均值分布(单位：mm)Table 1 Average precipitation distribution in different periods and regions before flash flood from 2013 to 2016(unit:mm).

根据不同地区山洪灾害发生频次与对应的不同时段的降水量分布(图5)，进行降雨临界阈值分析。从6—12 h降雨量来看，西南地区达到50 mm以上，山洪灾害数量明显增多，大于30次，东南地区降雨达到100 mm以上，山洪灾害爆发式增长，而北方地区灾害性降雨分布较为平均，在0～10 mm以上就呈现灾害多发的特点；西南地区3 h降雨达到10 mm以上、东南地区50 mm以上、北方地区0～10 mm以上，就需关注灾害的发生。小时雨强是山洪灾害发生的又一重要指针，对西南地区，连续降雨且小时雨强接近10 mm·h-1，山洪灾害多发，东南地区连续降雨且小时雨强达到50 mm·h-1以上，山洪灾害多发，对北方地区而言，小时雨强达到0～10 mm·h-1就容易出现山洪灾害。

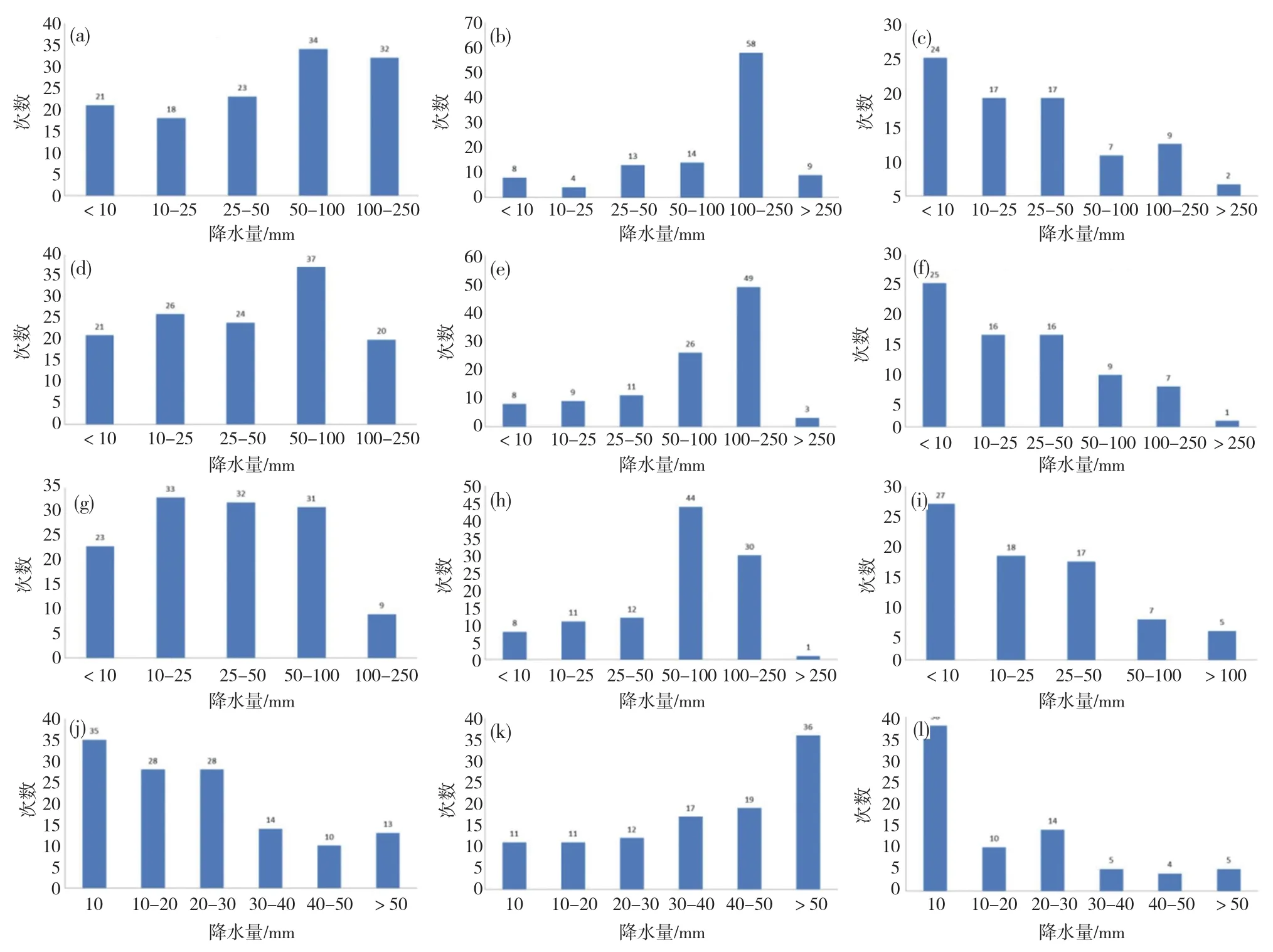
图5 西南地区、东南地区、北方地区山洪灾害发生频次与不同时段12 h(a、b、c)、6 h(d、e、f)、3 h(g、h、i)、1 h(j、k、l)降水量的对应关系Fig.5 Relationship between the frequency of flash flood disasters in the southwest,southeast and northern regions and the precipitation during different periods of(a,b,c)12 h,(d,e,f)6 h,(g,h,i)3 h and(j,k,l)1 h.

2.3 山洪灾害静态临界阈值推求

对不同时段降水序列引发的山洪灾害静态临界阈值进行分析，由于均一性检验、统计理论等都建立于固有假设的基础上，均要求进行分析计算的数据服从正态分布，而对于一般降水数据而言，具有明显非正态分布性质，因此必须将数据变为正态化(或者准正态化)。目前主要用到的数据变换为对降水量序列进行开平方、立方处理，对数变换，Box-Cox变换和John⁃son变换等，以提高降水量序列的正态性，本文通过对降水序列开立方处理，使降水数据成为较连续的正态分布降水因子(陈学君，2012)。以西南地区为例，通过计算各降水因子的概率密度，得到图6的散点分布，以高斯拟合建立概率密度函数，对该函数进行积分处理得到灾害概率的分布情况，通过不同的概率值对应的降水因子，确定降水临界阈值，以此推求灾害的静态临界雨量特征(张国平，2014)。

基于12 h、6 h、3 h及1 h降水因子及灾害发生频次分布的高斯拟合曲线(图6)，得到灾害概率公式

图6 西南区域不同降水因子与山洪灾害发生频次的关系及高斯拟合曲线图：(a)12 h降水；(b)6 h降水；(c)3 h降水；(d)1 h降水Fig.6 Illustration of precipitation factor during different time period(a)12 h precipitation,(b)6 h precipitation,(c)3 h precipitation,(d)1 h precipitation and frequency distribution of flash flood with Gaussian curve fitting in southwest region.

其中x为降水因子值，Y为该降水因子对应的灾害发生概率，σ为标准方差，μ为降水因子均值。x为12 h降水因子时，σ=1.43，μ=3.56；x为6 h降水因子时，σ=1.32，μ=3.29；x为3 h降水因子时，σ=1.20，μ=3.04；x为1 h降水因子时，σ=0.88，μ=2.60。

σ越小，说明灾害分布越集中在均值附近，σ越大，分布越分散。当降水因子处于均值附近时，发生灾害的概率大。根据上述公式，当西南地区12 h降水达到45 mm左右或6 h降水达到35 mm左右或3 h降水达到25 mm左右或1 h降水达到20 mm左右，山洪灾害发生概率均能达到50%。以此类推，东南地区12 h降水达100 mm以上、6 h降水达80 mm左右、3 h降水达60 mm左右、1 h降水达35 mm左右山洪灾害发生概率均能达到50%；北方地区12 h达25 mm、6 h达20 mm、3 h达15 mm或1 h达10 mm，山洪灾害发生概率达50%。根据上述公式，当西南地区12 h降水达到95 mm左右或6 h降水达到75 mm左右或3 h降水达到55 mm左右或1 h达到30 mm左右，山洪灾害发生概率均能达到75%。以此类推，东南地区12 h降水达170 mm以上或6 h降水达140 mm左右或3 h降水达110 mm左右或1 h达50 mm左右山洪灾害发生概率均能达到75%；北方地区12 h降水达60 mm或6 h降水达45 mm或3 h降水达35 mm或1 h降水达25 mm，山洪灾害发生概率达75%。此为静态临界阈值推求。

3 山洪降水动态阈值分析及检验

基于已有的山洪阈值分析技术，本文进一步开展了山洪致灾动态降水临界阈值技术研究。在山洪和降雨静态关系研究基础上，带入下垫面土壤含水量信息，建立基于灾害易发区土壤湿度的动态降水阈值技术方法。选取2013—2016年山洪灾害点信息，将山洪灾害发生前1 h、6 h、12 h和24 h的降水量值与降水过程前对应的土壤含水量信息进行相关分析，通过外包线分析进行灾害前降水与土壤含水量关系拟合，实现山洪灾害动态阈值判别算法的构建。当土壤干旱或湿度较小时，持续性的降雨通过大量入渗进入土壤各层，较少的部分形成地表径流，随着降雨的持续，流量增大，进而可能导致洪水灾害；若降水强度过大，超过土壤的入渗能力，则会在短时形成地表径流，根据降雨的强度，导致不同程度的洪水甚至山洪灾害。当地面土壤湿度较大，且处于即将饱状态，则少量的降雨也能快速形成径流引发山洪灾害。根据叶金印(2014)、陈瑜彬等(2015)的研究，降雨引发的山洪灾害发生前的土壤含水量与不同时间尺度的过程降雨量存在一定的关系，且随着时间尺度的增加，引发灾害的过程雨量受土壤含水量的影响增大。本文选取土壤重量含水率和土壤相对湿度因子作为土壤湿度的参数进行分析。

3.1 土壤含水率与降雨的关系

土壤重量含水率是指土壤中水分的重量与相应固相物质重量的比值，可表征土壤的干湿程度。本文分析370次灾害发生前的过程雨量与土壤含水量的关系。首先进行灾害点质量控制，剔除非降雨引发的灾害信息，并插值提取就近点的土壤含水量信息，选取距离灾害点半径10 km以内的土壤含水量信息，最终获取64个优质山洪灾害信息，随机选取其中的40个灾害点作为计算样本，剩余24个作为检验样本，基于灾害发生的不同时段降水过程开始前的土壤重量含水率信息及对应的各个时段降雨进行分析，发现搜集到的山洪灾害发生前50 cm以上的整层土壤初始重量含水率均达到10%以上，样本中灾害发生前的最高土壤重量含水率均不超过45%。而对于表层(10 cm)土壤层，初始土壤重量含水率均达到5%以上就可能在一定过程降水后发生灾害，而初始的最高土壤含水率为55%，由此可见，在山洪灾害发生前，土壤基本处于表层湿度较大，深层湿度较小的状态，土壤含水率与灾害前不同时段降水拟合关系较差，这是由于灾害点分布不均，土壤类型不同，相同的土壤湿度条件下，其土壤水分的有效性不同，因此该参数不便于在不同土壤间进行比较，需通过其他土壤含水量参数进行进一步分析检验。因此本文基于土壤相对湿度参数进行进一步分析。

3.2 基于土壤相对湿度的全国山洪灾害动态阈值分析及检验

土壤相对湿度即土壤含水率占田间持水量的百分比，相比于土壤重量含水量，土壤相对湿度更利于在不同土壤间进行比较。农业气象中通过以20 cm土壤相对湿度来分辨旱涝，而对于山洪灾害易发区而言，整层土壤的湿度判别均有指示意义。降雨入渗，蓄满产流或超渗产流形成地表径流进一步形成的山洪，不同于滑坡、泥石流等灾害，具有水流突发、水量集中，水流夹杂泥沙等特点，而地面表层土壤层是山洪夹带的表面物质的主体，因此洪水与表层土壤间的相关关系更为密切，常造成局部性的灾害。对表层土壤的湿度判别具有最直接的意义，为进一步分析370次灾害发生前的临界雨量与土壤湿度的关系，经过筛选，基于获取的40个最优灾害点提取样本土壤相对湿度信息和灾害实测降雨量值，进行样本散点的分布特征分析及自动曲线拟合，若能建立一条外包判别曲线(图7)，能使得大部分样本散点均分布在曲线上方，即土壤相对湿度一定的情况下，灾害实测降雨量均大于该判别曲线计算的降雨量值，即可认为当大部分的灾害发生时，该曲线都能有所反映，该曲线即为动态阈值曲线，且通过分析发现该曲线符合一定的指数函数特征，指数函数的斜率随着时效明显增加，斜率渐增，说明时间尺度越大，与土壤相对湿度的相关性更强。同时，对次表层(50 cm)土壤，及整层土壤，也同样存在此相关关系，但函数关系规律不明显。

图7 降雨量与土壤相对湿度的相关关系图Fig.7 Scatter plot of precipitation and relative soil humidity.

建立指数相关关系后，本文选取一定检验样本，并用命中率来对各层土壤及不同时效的降水来进行检验，当灾害检验样本在一定土壤湿度条件下，对应的降雨量大于判别曲线上对应的动态降雨量值时(图7)，即当检验散点落在曲线上方时，则认为该样本正确命中。选取24个灾害点检验样本进行模型检验，命中率如表2所示，如以50 cm以上整层土壤含水量和灾害前日降雨量因子进行建模，并用24个灾害点检验样本进行检验，92%的灾害点在模拟曲线上方，即命中率92%。检验结果表明，基于各层土壤含水量建立的降雨动态阈值计算方法，对山洪灾害的命中率较为平均，75%—92%的检验点实测降雨都高于计算的动态雨量临界阈值。

表2 基于不同层次土壤和时效的降雨量动态阈值模型命中率Table 2 Hit ratio of dynamic critical precipitation threshold model based on different soil layers and time.

根据命中率检验结果，同一时效的降雨量，对应不同的土壤层建立的判别曲线，检验命中率不同。选取命中率较高的土壤层指数判别法，得到不同时效动态阈值指数计算方程，其中x为土壤相对湿度，y即为对应的降雨阈值。具体方程如下：

基于小时雨强的动态阈值(基于10 cm土壤含水量信息方程)，y=159.96e-0.024x

基于6 h降雨量的动态阈值(基于10 cm土壤含水量信息方程)，y=405.46e-0.025x

基于12 h降雨量的动态阈值(基于50 cm土壤含水量信息方程)，y=5801.1e-0.066x

基于日降雨量的动态阈值(基于50 cm以上整层土壤含水量信息方程)，y=377.99e-0.029x

这种表征全国的计算关系，通过已知土壤相对湿度的情况，可以推求不同时间尺度的降雨是否达到最小临界雨量，然而由于各地的地质结构及土壤类型差异较大，已知的计算关系可较好地预测是否有发生灾害的趋势，但对于典型区域的指针意义，并不明确。

3.3 基于土壤相对湿度的西南地区山洪灾害动态阈值分析及检验

由于研究所用的灾害点信息分布不均匀，多集中在西南地区，因此本文提取西南地区这一典型区域进行进一步研究。选取灾害点20 km以内的土壤监测信息，提取46个有效灾害点，其中31个作为计算样本，15个作为检验样本，以10 cm土壤湿度及50 cm以上整层土壤湿度作为代表土壤含水量参数进行最小外包线拟合，得到西南地区表层及整层土壤含水量与降水量的动态关系(图8)。

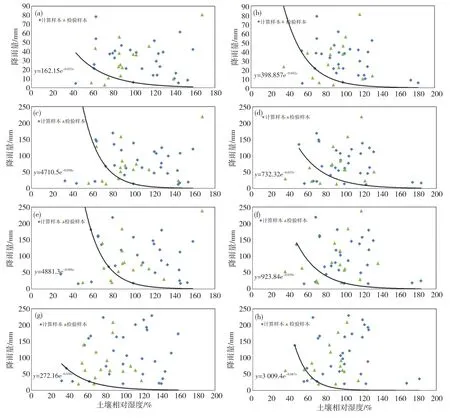
图8 1 h、6 h、12 h、24 h降雨量与10 cm土壤相对湿度（a、c、e、g）及50 cm以上整成相对湿度（b、d、f、h）的关系Fig.8 Relationship between 1-h,6-h,12-h,24-h precipitation and the relative humidity of 0-10 cm soil(a,c,e,g)and 0-50 cm soil(b,d,f,h).

基于15个西南地区山洪灾害点检验样本信息对此外包曲线进行检验，命中率如表3所示，检验结果表明，基于10 cm土壤含水量的降雨动态阈值计算方法，对山洪灾害的命中率更高，对15个检验灾害点中，73—93%的灾害点不同时效降雨都高于计算的动态雨量临界阈值；而基于50 cm以上整层土壤的平均含水量的计算方法，所计算的动态阈值命中率为67%—87%。

表3 基于不同层次土壤和时效的降雨量动态阈值模型命中率(西南地区)Table 3 Hit ratio of dynamic critical precipitation threshold model based on different soil layers and time periods(the southwest region).

根据命中率检验结果，西南地区的基于10 cm土壤含水量计算的动态阈值结果命中率较高，因此确定不同时效动态阈值指数计算方程，如下：

基于小时雨强的动态阈值，y=162.15e-0.033x

基于6 h降雨量的动态阈值，y=4710.5e-0.058x

基于12 h降雨量的动态阈值，y=4881.3e-0.056x

基于日降雨量的动态阈值，y=272.16e-0.036x

根据检验，西南地区小时雨强、6 h降雨量、12 h降雨量和日降雨量的山洪动态降水阈值模型的命中率分别为80%、73%、73%、93%，而对应的基于阈值的山洪静态模型命中率分别为67%、67%、73%和86.7%，动态模型在1 h和6 h的命中率上提高了约10%。

2014年8月11日，贵州毕节地区纳雍县阳长镇海子村八组发生小型山洪灾害，造成1人死亡，灾害发生当日最大6 h降雨量仅为23.7 mm，而该点静态临界阈值模型临界雨量为35 mm，未到预报级别，究其原因，是因为前期降水充分，土壤相对湿度条件已达到140%，只要较少量的降水即可激发灾害，在动态阈值模型中，考虑到了这一特点，达到了模型预报级别，另外，在其余不同时段的降雨动态模型中，均体现了这一特点，因此对动态阈值的统计研究具有一定的参考价值。

4 结论与讨论

应用统计法分析山洪灾害和前期降水的时空分布特征，通过不同时段降水量级的频次分布，探讨灾害的静态降水阈值，在静态阈值分析的基础上，提取土壤湿度因子，土壤重量含水率及土壤相对湿度信息，开展降水与不同土壤含水量的研究，通过最小外包线拟合，建立山洪灾害的降水动态判别曲线，建立基于土壤相对湿度和降水量的指数计算方程，该方程可基于当前的土壤湿度信息及未来不同时段降雨量信息，预报山洪灾害是否可能发生，并对预报方法进行了试验检验，均取得了良好的效果，并得出以下几点结论：

(1)山洪灾害点主要分布在西南、东南、西北地区东部、华北等地，分布密度最大的是西南地区，其中以云南、贵州、四川、重庆等省市分布最广。每年的5～9月是山洪灾害高发期，尤其是6～8月，山洪灾害以爆发式增长。

(2)山洪灾害前降雨较多分布在灾害前24 h以内。当东南地区24 h降雨达到100 mm以上时易发生山洪灾害，北方和西南部分地区24 h降雨达到25～50 mm就易发生山洪灾害，局部地区甚至达到10 mm以上就需要引起关注；从6—12 h降雨频次分布来看，西南地区达到50 mm以上，山洪灾害数量明显增多，东南地区降雨达到100 mm以上，山洪灾害爆发式增长，而北方地区灾害性降雨分布较为平均，在0～10 mm以上就呈现灾害多发的特点；3 h降雨西南地区达到10 mm以上、东南地区50 mm以上、北方地区0～10 mm就需关注灾害的发生；小时雨强是山洪灾害发生的又一重要指针，对西南地区，连续降雨且雨强接近10 mm·h-1，山洪灾害多发，东南地区连续降雨且雨强50 mm·h-1以上，山洪灾害多发，对北方地区而言，雨强达到0～10 mm·h-1就具备山洪灾害风险。

(3)建立了各时效降雨与各层土壤湿度间的指数关系，且指数函数的斜率随着时效的延长明显增加，时间尺度越大，引发灾害的过程雨量受土壤湿度的影响越大。建立了全国及西南区域的土壤相对湿度和各时效降水的指数判别方程，可用于不同土壤湿度条件下不同时效临界降雨阈值的动态计算，从而通过与未来不同时段的降雨预报的比较，进行灾害有无的判别。通过检验表明，各层土壤含水量因子中，山洪灾害阈值与10 cm土壤含水因子关系最为密切，全国及西南地区的动态阈值预报方法命中率评分均能达到70%左右。

目前，该方法已在国家级山洪灾害预警业务中进行试验，在2020—2021年的汛期山洪灾害预警业务中正式应用，但是由于国家级业务中获取的灾害点信息大多来源于各省的灾情直报系统，与洪涝灾害等信息较难区分，灾害点信息较难精确到具体时次，且土壤湿度观测站点较为稀疏，大多位于地势相对平坦的区域，在山区信息极少，资料有限使得统计方法存在一定的局限性。如何通过耦合分布式水文模型获取下垫面精细化的土壤墒情，如何进一步结合精确到时次的灾情，对判别方程进行优化更新，是下一步需要重点研究的工作(郭克等，2016；郭亮，2018；管晓祥，2017；李昌志等,2015)。