全站仪自动化监测中的控制测量和坐标传递

王伟才，杨晨辉，彭成山，刘仁钊

（1.上海地矿工程勘察有限公司，上海 200072；2.湖北国土资源职业学院 测绘地理信息学院，湖北 武汉430090）

目前，轨道交通保护监测所占的市场份额逐步增加，仅苏州市场容量已超过3 000万/a。保护监测工作因其对人员要求高、技术要求高、仪器设备要求高以及可持续性等行业特点，受到市场高度关注；同时，市场对轨道保护监测技术开发、应用研究的力度也不断加大。自动全站仪、静力水准仪、电子水平尺、光栅光纤、近景摄影测量、激光三维扫描等自动化监测技术已被广泛应用于轨道保护监测行业中[1-2]。

轨道交通自动化监测系统采用的技术较丰富，如在国外，英国伦敦Crossrail轨交工程中采用的CsattAR像素跟踪监测系统、美国洛杉矶区域连接线轨交工程采用的由柔性线缆式传感器与传感接头组成的ShapeArray自动化地层监测系统等，其技术方向有所不同；在国内，苏州、杭州、南京等一些城市在轨道保护监测的技术选型上，普遍采用自动全站仪监测系统，控制网布控多采用自由设站，计算方法采用后方交会或坐标转换，另辅以人工检核，以保证数据的准确性[3]。

在隧道内实施全站仪自动化监测的方法中，实时获取测站点的坐标，是其关键技术之一。由于测站一般处于变形区域内，因此需将测站两端的基准点坐标实时传递给测站。然而，隧道内较狭小，降低了自由设站方法的适应性，在多测站的坐标传递中，后方交会方法经过多次运用后，其图形强度的问题较突出。鉴于此，本文通过实例计算分析了后方交会方法的应用特点，提出了通过测边三角形进行测站坐标修正的方法；并基于全站仪自动化监测技术在隧道监测中的应用，论述了测站坐标传递网形设计、测站点位移修正与检验方法，具有重要的现实意义。

1 坐标传递网形设计

1.1 控制网设计

以苏州为例，地铁隧道衬砌外径一般为6.2 m，内径为5.5 m，车站平均间距约为1 200 m。处理带状线路时，首级控制网采用导线形式较合理；而在隧道内测设闭合导线并非均能解决实际问题。导线的往返经常存在多线段重合的情况，闭合导线常演变为往返测导线。与单线路重复测量相比较，闭合导线在线路 两端多了两个折返角。总的来说，闭合比不闭合的条件好；在线路两端增加三角形比单一导线的多余观测数多；采用导线形式，转折点越少，精度越高。从误差理论来说，控制点的精度主要由观测值、图形强度和平差模型的精度构成。因此，提高点位精度的办法主要包括：①改善控制网各点之间的几何关系，以增加多余观测数；②通过重复观测，提高观测值精度； ③选择合适的平差模型。

综上所述，在隧道内进行控制网布控，条件较严苛。无论采用何种方法进行坐标传递，均需减少后期进入隧道进行控制复测的次数，首先应选择好坐标传递网形；然后设计好首级控制网形；最后对首级控制网、坐标传递网、测站设置以及后期的控制网人工复测部分、测站自动复测部分进行整体设计。本文采用在隧道内测设的实验数据对上述方法进行探讨。

1.2 坐标传递网形

若测站位于变形区域内，则常将测站坐标认为是待定的。通过测站变形区域外或在某一时刻内相对稳定的基准点进行观测，并以此来实时计算测站坐标的过程，称为坐标传递。无论单台或多台全站仪施测，根据现场条件，可采取后方交会、测边三角形、三角形混合导线等形式进行组网，如图1所示。

图1 多台全站仪坐标传递组网[4]

图1 a中T1、T2为测站，A、B、C、H、I、J为已知点，通过首级控制确定，E、F、G为坐标传递公共点。当T1、T2位于变形区域时，通过两端已知点，采用自由设站的方式可获得两组E、F、G公共点的坐标值，再通过坐标系统转换可获得统一坐标系下的精确值。图1b中T1、T2为测站，且相互不通视，A、B、E、F为已知点，通过首级控制确定，D、C为坐标传递公共点，该类网形可按测边三角形进行整体解算。图1c中T1、T2为测站，相互可通视，A、B、C、D为已知点，通过首级控制确定，同时在全站仪上加装观测手柄，则可获得T1与T2之间的方向角、距离，再和两端已知点构成三角形混合导线，进行整体解算。

2 近似值的计算误差

通常采用自由设站的方式实时计算测站点坐标。由于隧道内布控条件限制等客观原因，使得采用余切公式计算所得的测站点坐标近似值存在一定的变形，采用测边三角形计算的近似值也存在一定变形。经过初步计算，其变形原因与图形强度密切相关，如图2所示。

图2 测站坐标计算构图

1）余切公式近似值的误差问题。由余切公式计算构图可知，按余切公式计算P点坐标点位中误差的 公式为：

在隧道内采取后方交会自由设站方式所获取的图形中，A、B、C三点的相对位置较近，使得边长a、b较短。将全站仪架设在P点，所能观测的量为Sa、Sb、Sc、∠ρ、∠α、∠β。设由已知点A、B、C点构图所得a=b=30 m，Sa=Sb=100 m，Sc=105 m，全站仪的测角精度为0.6″，∠γ=∠δ=165e，代入计算，得到M=2.9 mm。与此同时，分别计算γ=δ= (130 165 170 175)所获得的相应精度，得到M= (1.5 2.9 4.2 8.3)。由此可见，随着图形条件的变化，按余切公式计算得到的坐标变形逐步增大。

2）测边三角形近似值计算变形问题。由测边三角形公式计算构图可知，B、D点为已知点，C点为测站点。由于三角形高h与方位角αBD存在加减90e的关系，C点坐标的计算公式为：

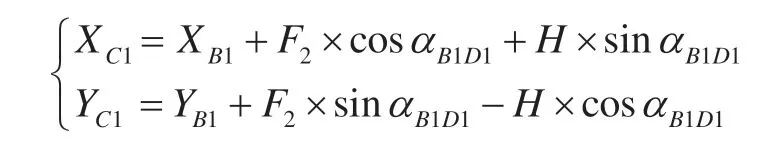
相对于余切公式而言，其C点坐标误差主要来源于已知点B、D的方向角以及采用三边计算所得高的误差，其计算过程中的变形会对C点坐标有一定的影响，但影响较小。根据误差传播规律，在R2阶计算空间内，设B点坐标为(X1,Y1)，D点坐标为(X2,Y2)，其高h的方差计算公式为：

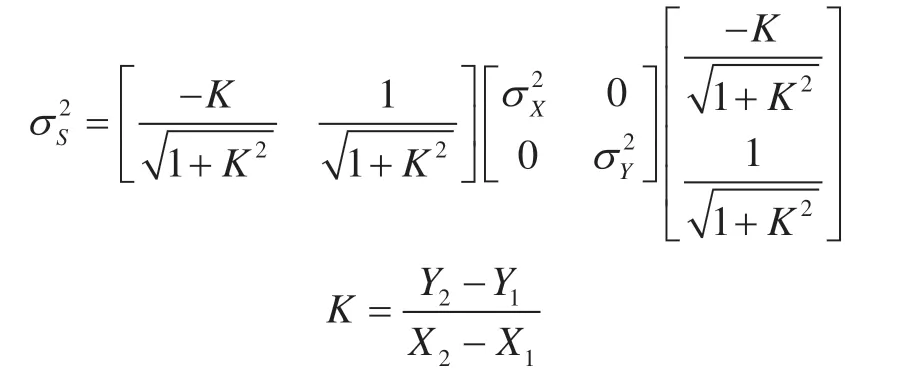
设B点坐标的精度=0.103 26，则有：=

3）近似值计算产生的变形问题。由于测站常布置在变形区域内，因此测站点的坐标始终为待定的。对已知点进行观测后，需将已知点坐标通过观测量传递到测站，计算近似值。采用余切公式计算所得近似值与精确值之间存在变形，距离近似值与观测值之差约为30 mm；采用测边三角形计算的近似值，变形相对较小，主要表现为测站点所成夹角上的变形。

3 测站点精确坐标的计算

3.1 后方交会方法的验后估计

以图2所示的测站坐标计算构图为例，本文对 3点分布于测站一端的布控方法，做了多次偿试，但无论布置在测站一侧或是交错布置，总有一点所构图形角度非常小，通常小于1e，严苛情况下，不到20′， 3点构图几乎在一条直线上。作为固定点不动的测站点布置位置与CPIII布控不同，其全站仪无法安置在隧道中间部位，隧道上部为接触网，下部为道床轨道，只有左右两侧隧道结构可安置全站仪，且只能通过上下调整来均匀其夹角，但全站仪与控制点之间的距离很短。通过多次偿试，本文测得一组数据，如图2a所示，将全站仪设置在P点上，A、B、C为已知点，在P点上分别对A、B、C的边长和角度进行观测，获得的数据如表1所示。

表1 隧道内自由设站观测数据表

1）基于表1中的数据，利用余切公式计算P点的近似值坐标，得到Xp=51.555 03，Yp=-362.354 19。

2）采用间接平差的方差分量估计法计算得到P点至各已知点的误差方程和系数，并组成误差方程组。设测站点P的坐标为参数，则有误差方程组：

3）间接平差的赫尔默特方差估计。根据经验，测角中误差为f0.5″，边长测量中误差为0.67mm[5]，则Pβ=1，Ps=0.557，构建方程：

表2 赫尔默特法的估计结果[8]

4）精度评定。本文采用第三次迭代计算结果进行精度计算，得到；通过σ02×Q可得

5）方法评价。采用余切公式计算得到的坐标近似值误差较大，间接平差时，利用6个方程计算两个参数的值，其中任意两两组合均可能有一组解；按照最小二乘原理求解，实际上是求得两个参数同时满足 6个方程的最优解。在后方交会方法中，按照经验估计精度定权，其角度与边长分量实际上并不够精确，通过验后估计计算，前两次的单位权方差并不一致，且差距较大；第三次估计的分量方差趋于一致，且边长的权值较大，说明其精度较高。总的来说，观测值误差、图形强度、计算模型误差在后方交会的总体精度构成中均有体现，其中图形强度的影响 最大。

3.2 测边三角形方法

如图2b所示，以D、B两点作为测站点C的工作基准点，分别测得C-B、C-D的距离以及夹角β构建测边三角形。在每次对其他点进行测量前，先以C点为测站，观测基准点D、B，观测4个测回，测量数据如表3所示。

表3 已知坐标与测站观测量

根据间接平差，该图形有2个边长误差方程和 1个方位角误差方程，以待定点C的坐标(XC,YC)为参数，B、D为已知点，则有：

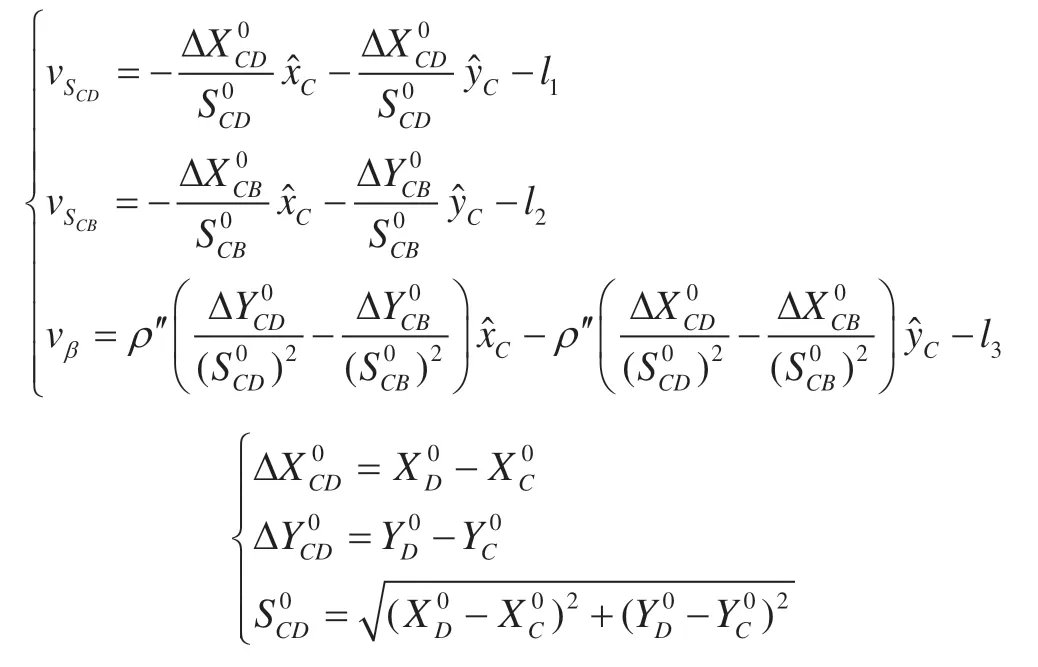
计算近似角值，得到l3=-22.2″，进而得到误差方程为：

按照全站仪标称精度定权进行预平差，令P=diag[0.664 6 0.837 31]，得到。C点精确坐标为(46 096.033 84,64 452.629 27)。将代入误差方程中，则有V=[0.298 7 0.236 3 0.004 8]T。

在本次计算中，共有3个误差方程和2个必要观测数，因此r=n-t=1，得到：

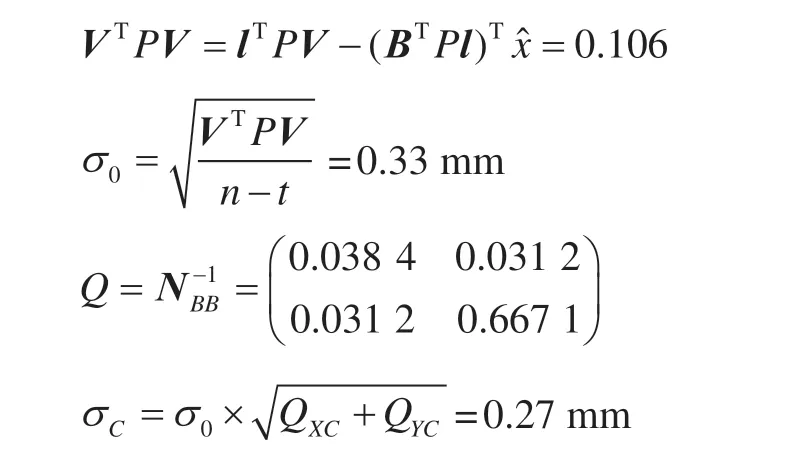
由此可见，采用单方向4测回对边角进行观测的模式，在约200 m范围内，其精度为0.27 mm。在平差精度满足要求的前提下，其成果均可采用[9]。本文不再对其进行验后估计。

4 测站点坐标的稳定性检验

4.1 观测精度的差异性（F检验）

由于监测的特点是多次重复观测同名点，从而获取各期的变形量，在测站上获取的边长、角度均相近，因此本文采用F检验对观测精度的差异性进行检验。

1）F检验。采用双侧检验（双尾检验），服从F（n1-1,n2-1）分布的统计量为：

2）在该检验中，自由度的确定主要采用测回数。其主要原因为：①因在测站点位移修正方法中，首先需对测站进行多个测回的观测，获取较准确的观测数据，并进行计算，其方差较小，采用F检验时，以该期平差值为基础，即作为一个检验的“标准”，若后期的观测成果方差与该期结果精度等同，则认为观测数据合格；②与同名参数的检验不同，其采用样本方差进行检验、而非均方差，且严密平差本身对误差进行了更合理的分配，获得了更接近于真实值的测站坐标，其最小二乘原理本身为无偏估计，方差本身又代表了各次测量值的离散程度，即将某一组向量观测了4次，通过计算获得的方差，因此从本质上说方差与其各个量的观测次数密切相关，在测边三角形方法中，采用该测站上的测回数作为自由度较为合适； ③若采用多余观测数作为自由度，单测站的观测量有限，而按构图进行严密平差，其多余观测数更多地反映了图形强度情况，无法体现一个观测量观测多次对成果精度水平提高的效果，且在自由度均为1的条件下，F值很大，则两次方差之比的区间很大，即便数据本身误差较大，检验时仍有可能是合格的，此时，采用多余观测数作为自由度是没有意义的。

4.2 同名参数差异性的检验（t检验）

显然，若对控制网采用间接平差，则有：

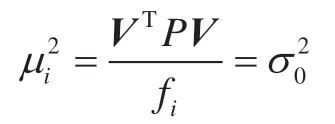
式中，f为多余观测数[10]。

、分别为两期观测数据的平差值；为两期观测数据平差值归算为基线垂直方向之差；S1-S2=0.611 mm。

利用上述计算方法得到：第一期Q1==，第一 期高h的方差为=0.005；第二期Q2==，第二期高h的方差为=0.034 9。

原假设H0：在H0成立下，t分布的统计量为：

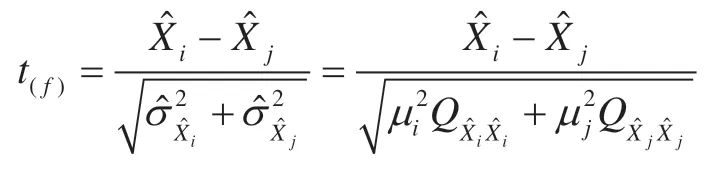
5 结 语

本文利用点线方程（或三角形的高h）和边角网的误差计算公式、后方交会验后估计对数据检验的自由度如何使用、确定等问题进行了推导和论述，使得自动全站仪系统在轨道保护监测中的应用，控制网、坐标传递、测站点位移修正、检验判别等子模块中的技术要求以及数据处理方法的应用更加清晰。在隧道内对部分近似值的计算公式进行了相应实验，并根据实验数据进行了验算，为测站点坐标的位移修正与检验提出了一种新的更简便的基于三角形解算的方法。通过在苏州轨道交通2号线保护区内的龙湖项目，4号线保护区内的4号地块、11号地块项目，宁波轨道交通2号线等项目中的实践发现，该方法能有效解决实际问题，具较好的应用价值。