数值水槽模拟波浪运动及合理性研究
杨彤麟,罗 浩,晏 亮,甘贤备,郭 辉
(1.湖南科技大学土木工程学院,湖南 湘潭 411201;2.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081)
环境条件一直是桥梁等结构设计需要考虑的一大关键因素,在某些情况下要面对跨越水域的需求及波浪冲击桥梁的问题,由于在现场进行测量难度大,成本高,又为了能方便准确地进行波浪对结构产生的冲击作用方面的研究,国内外学者在波浪模拟上做了大量地相关研究。
Peter Troch[1]首次实现了推板造波法及边界消波,减少了水槽长度,大幅降低了边缘反射效应;刘毅[2]指出现有造波机在一定频率范围下振幅保持和精确控制等方面的问题,提出应用于造波机的新型液压驱动技术;叶潇潇[3]研究了不同造波条件下生成的内孤立波运动的流场特征;张可心[4]采用二阶造波理论,分别进行了物理水槽和数值水槽造波实验;虞佳颖[5]利用fluent探究了预留冲刷坑对挑流水舌在下游水垫塘中消杀能量的效果。
由于造波实验水池的成本较高,试验结果受影响因素多,本文总结了指导造波的波浪理论,并从数值水槽方面,总结了其造波方法和消波的原理,并以一个工程实例验证了数值造波的模拟效果。
1 波浪理论
当前学者们一般把波浪模拟分为3种:理论推导、物理模拟及数值模拟,所以波浪研究常采用理论及物理模拟或者理论及数值模拟。在进行数值模拟波浪运动时,假定波浪为一种不可压缩的无黏性的理想液体,其流体运动的速度势函数Ф(x,y,z,t)满足的连续性拉普拉斯控制方程为[6]:
∇2φ=0
(1)
在描述波浪运动的同时,给定其水深为d的初始边界条件为:
(2)
其自由水面z=η(x,t)时的运动方程可由伯努利方程积分得到:
(3)
式中,g—重力加速度。
波浪沿x方向传播则满足周期性边界条件[7]:
φ(x,t)=φ(x+L,t)
(4)
φ(x,t)=φ(x,t+T)
(5)
式中,L—波长;T—波浪周期。
1.1 线性波浪理论
研究人员最初假定波浪运动的幅值很小,仅对边界条件取理想的线性化处理,将重力作为唯一外力,从而水质点保持不变的频率进行往复运动,波面呈简谐波式并以一定波速传递,这便是线性波浪理论,又称为小振幅波浪理论,其波面方程为:
(6)
水质点的水平与竖直方向速度分别为:
(7)
(8)
波速C为:
(9)
式中,k—波数;z—距水底距离;η—瞬时波面高度;H—波高;ω—波的圆频率。
1.2 斯托克斯波浪理论
由于线性波忽略了波高对波浪作用的影响,研究人员进而把波陡(波高/波长)作为参数,得到了非线性的stokes波浪理论,其波面方程为:

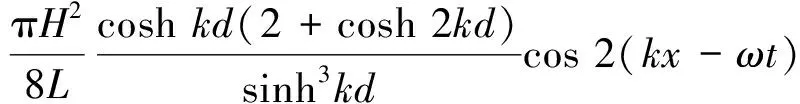
(10)
水质点水平方向的运动速度为:

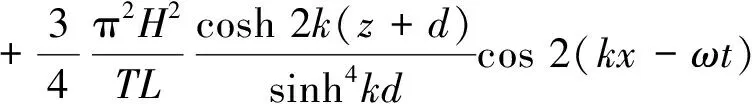
(11)
水质点竖直方向的运动速度为:


(12)
二阶stokes波波速与线性波相同,其波长为:
(13)
式中,L—波长;T—波浪周期;H—波高;η—瞬时波面高度;z—距水底距离;k—波数;d—水深;ω—波的圆频率。
1.3 椭圆余弦波浪理论
相对于线性波及斯托克斯波来说,椭圆余弦波是一种适用于近海岸区的非线性波浪理论,其具有更陡的波峰和更平坦的波谷,能在浅水条件下更明显地反应波浪运动的主要因素,波面方程用雅可比椭圆余弦函数表示为:
(14)
(15)
Zt=ZC-H
(16)
式中,Zt—地面与波谷底端的垂直距离;ZC—地面与波峰顶的垂直距离;k—椭圆积分模数;Kk—k的第一类完全椭圆积分;Ek—k的第二类椭圆积分;Cn—椭圆余弦函数,当0 孤立波是一种在长距离传播中可以较好地保持波浪形态以及波浪能量的非线性波浪理论,它一般用于在浅水条件下,波浪冲击船舶等物体破碎或产生极端波浪的情况。当式(14)、(15)中k=1时,波浪为孤立波;当k=0时,波浪为线性波。 速度入口造波是提供一个目标波的水平及垂向运动速度给入口边界处的水质点,促使水质点周期性运动进行造波。数值波浪水槽的造波区入口处需要将边界设为速度入口边界,边界入口定义的入射波形式为: H=Acos(kx+ky-ωεt+ε) (17) 式中,kx=kcosθ;ky=ksinθ;A—振幅;ε—相位差;k—波数。 有效波频率定义为: ωε=ω+kU (18) 式中,U—入射波速度;ω—波频率。 该方法是通过fluent自带的二次编译功能在造波源区域给动量方程添加动量源项s(x,y,t),使水槽入口处水质点拥有运动速度,此时水面将在重力作用下进行升降,从而形成波浪。其动量源s(x,y,t)可用以下公式确定: (19) (20) 式中,u(x,y,t)—t时刻目标波浪在坐标(x,y)处的水质点水平速度,根据线性波理论或Stokes波理论取值;u、v—x、y方向速度;Δx—水平方向网格长度。 质量源造波与物理实验中的推板造波机的原理相同,将入口处固壁边界处理成动网格来模拟推波板运动。其水平运动速度函数u(t)如下: (21) (22) 式中,η—波面升高,根据Stokes波理论或线性波理论确定其值;ω—角频率;C0—造波板运动与给定波浪间的传递函数;k—波数;d—水深。 在物理水池实验中,经常需要在水槽末端布置海绵等多孔介质吸收波浪,这是为了避免反射波对造波效果产生影响。所以在数值水槽的末端可以同样设定一定长度的多孔介质区域,用以达到吸收反射波的效果,保证数值消波的合理性。 其原理是在消波区域的动量方程中添加动量衰减的源项,从而达到消除波浪的作用,该源项表达式为: (23) 式中,第一项为黏性耗散项;第二项为惯性耗散项;v—速度;1/α、C2—常数。 考虑到该动量源过大会对工作区域来波产生影响,所以仅设置一个合适的惯性耗散系数C2,并将此系数沿波浪传播方向线性递增,则在消波区x=xi处有[8]: (C2)i=KP[(xj-x0)/(xe-x0)] (24) 式中,x0、xe—消波区前端和尾端的横坐标,x0 动量阻尼消波方法的消波原理是在数值水槽末端的消波区域设定一个动量源,将运动方向设为波浪传播反方向,相当于提供一个与波浪运动方向相反的阻力项。阻尼消波的动量方程为: (25) (26) 式中,ρ—流体相对密度;t—波浪传播时间;u—波浪传播的水平方向的速度分量;v—波浪传播的竖向速度分量;p—划分流体网格单元上的压力;g—地表重力加速度;μ—消波动力系数。 本文基于FLUENT计算流体软件,采用VOF法追踪水气交界面[9],以不可压缩黏性流体的N-S为时均控制方程,采用k-ε湍流模型,并以PISO算法的二阶迎风格模式进行求解计算,从而得到了合理的数值结果。 根据某一大跨斜拉桥桥塔样式建立数值水槽,并根据造波区与消波区长度[10]设定长为368m,宽度为125m,高为250m,水深为40m,选取有效波高Hs为6.4m,有效波周期为7.38s,波长为84.50m。数值水槽网格划分采用六面体结构化网格,在波浪传播方向的网格均采用0.15m加密网格处理,在水槽竖向以自由水面为界采用渐变网格加密处理,网格尺寸在0.25~1m之间,为了更加精确反应桥墩壁面上所受到波浪力作用大小,对桥墩流域处的纵向网格设置边界层加密到0.1m。最后划分了2140000左右个网格单元,网格质量均在0.6以上符合计算要求,网格划分如图1所示。基于2种不同波浪理论的造波结果,线性波与stokes波的波面时程对比如图2所示,水质点速度对比如图3所示。 图1 网格划分图 图2 波面时程 图3 水质点速度 从图2中不难看出,由于Stokes波在加入波陡参数后,其理论下的波浪波峰较线性波更陡,波谷较线性波更平坦。同时从图3中看出线性波与Stokes波水质点水平速度与竖向速度基本保持一致。 基于fluent造波方法中,源造波及推板造波需要使用动网格技术,并且波高随水域衰减快[11],本文采用造波效果更好的速度入口造波,消波区通过在fluent软件设置自定义UDF,编写对应数值阻尼源项宏的消波代码,最后得到数值结果与理论值的对比结果如图4所示。 图4 数值模拟与理论计算对比 由图4可知,由于采用速度入口造波,在距入射边界处100m的前15s,波浪尚在传递,此处水面呈发展状态,在23s处和理论值得到了较好的拟合,并保持稳定,误差较小,波高衰弱较小,得证数值模拟效果良好。 本文首先介绍当前主要的4种波浪理论,再系统地总结了当下数值模拟波浪研究主要采用的造波及消波方法,通过建立一个实况斜拉桥桥塔的数值水槽,得到了波浪数值解,并与理论界对比,分析得到以下结论: (1)当前主要波浪理论为线性波浪理论,非线性斯托克斯波浪理论,椭圆余弦波及孤立波。通过fluent软件发现stokes波波峰较线性波更陡,波谷较线性波更平坦,但线性波与Stokes波水质点水平速度与竖向速度基本保持一致。 (2)当前数组模拟波浪研究主要采用的造波方法为:速度入口造波方法、动量源造波方法、质量源造波方法等;消波方法有:多孔介质消波方法、动量阻尼消波方法等。 (3)基于fluent计算流体软件,采用stokes波,速度入口造波方法及动量源消波方法得到的数值模拟解与理论计算解拟合较好,验证了数值造波的可靠性。1.4 孤立波浪理论
2 数值造波
2.1 速度入口造波方法
2.2 动量源造波方法
2.3 质量源造波方法
3 数值消波
3.1 多孔介质消波方法
3.2 动量阻尼消波方法
4 数值模拟
4.1 工况条件及网格划分


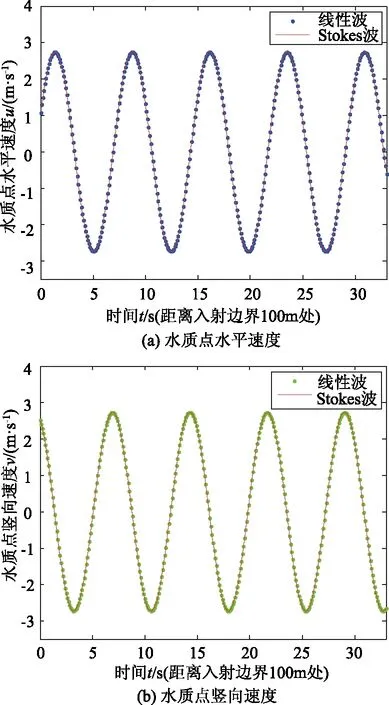
4.2 数值结果对比

5 结论

