基于卫星高度计数据的全球海洋潮汐特征分析*

许安迪， 陈学恩

(中国海洋大学海洋与大气学院，山东 青岛266100)

由于潮汐的海洋观测易受仪器、天气、地形和经济的制约，难以得到长期的大面站观测资料，而通过星载雷达高度计可以对海平面高度、有效波高和后向散射进行全天候检测，故自1970年代海洋卫星测高技术兴起，潮汐的研究就开始趋于依赖高度计测高技术。特别是1992年发射升空的TOPEX/Poseidon(以下简称T/P)及其后续卫星，数据质量有明显提高[1]，为物理海洋学研究提供了重要资料，在潮汐的研究方面取得了丰硕成果。

最先从卫星高度计数据中提取潮汐信息的是Cartwright和Ray[2]，他们通过Geosat高度计卫星第一年的数据对全球潮汐进行研究，给出了第一个基于卫星高度计数据的全球潮汐模型。此后，Ma等[3]利用T/P卫星第一年的观测数据，对Cartwright和Ray[2]给出的模型进行了校正。关于利用高度计资料提取潮汐信息的研究，国内学者做了大量工作，但大多聚焦于中国近海[4-10]；而在全球海域的研究较为匮乏，如沈春等[11]通过10年T/P资料对四大分潮进行了分析，Wang等[12]利用16年T/P及Jason-1卫星资料聚焦于八大分潮的分析，宋箐阳等[13]对18.61年高度计数据进行分析，并探究了不同数据长度对分析结果的影响，但涉及通过高度计数据探究长时间跨度上全球潮汐特征变化的研究颇少。

随着全球气候变暖，海平面不断上升。李大炜等[14]利用T/P、Jason-1及Jason-2高度计卫星的海面高数据和验潮站数据分析了全球海平面变化趋势，表明在1993—2011年间全球海平面以(3.12±0.4) mm/a的速率上升。海平面上升会减小陆架浅水区的底摩擦及侧摩擦作用，从而导致潮波传播发生变化，造成潮差及潮时的变化[15]。而近年来兴起的填海造陆等人类活动也必然会导致岸线地形的变化。孟云等[16]利用FVCOM模型，基于2004年和2014年的渤海岸线地形资料，证明当岸线地形变化时，潮波系统和潮流性质也随之发生改变。综上，气候变化和人类活动造成的海洋状态改变将对潮波系统产生一定影响。月球白道面与地球赤道面之间的夹角称为月球赤纬角，其变化周期为18.61年，也就是最长的分潮周期。那么在18.61年跨度上，全球海洋的潮汐特征究竟存在如何的改变？这是本文所关心的问题。

本文采用18.61年(1992-10-03～2011-04-29)的T/P，Jason-1和Jason-2卫星高度计沿轨数据，通过验潮站实测数据和同潮图探讨验证了高度计资料应用的可靠性与准确性；在此基础上，对比分析了特定时段资料，即该18.61年中最初2.97年(1992-10-03～1995-09-18)和最末2.97年(2008-05-13～2011-04-29)的结果，以探究在18.61年变化周期跨度上M2分潮特征的变化。

1 数据与方法

1.1 卫星数据

TOPEX/Poseidon(以下简称T/P)高度计卫星于1992年8月10日由法国太空总署(CNES)和美国太空总署(NASA)联合发射升空，轨道周期为112.0 min，重复周期为9.915 6 d。卫星环绕地球多圈后回到原位置对应的星下点轨迹被称为一个cycle，每环绕地球一圈中最南和最北两端之间的星下点轨迹被称为一个pass；一个cycle包含127个公转圈数，即254个pass，其中单行为上行，双行为下行。位于赤道处的卫星离地参考高度为1 336 km，相邻轨道距离为315 km。T/P卫星开始记录数据(cycle 2)的时间是发射同年的10月3日。

Jason-1卫星于2001年12月7日发射升空，2002年1月15日开始记录数据。在Jason-1卫星发射7.5年之后，Jason-2卫星于2008年6月20日发射升空，同年7月12日开始记录数据，时至今日仍在运行。Jason-1和Jason-2卫星作为T/P卫星的后续继任，重复周期和初始轨道均与其一致。

本文采用的数据来自宋箐阳等[13]处理后的高度计沿轨数据，在卫星覆盖的全球海域内(66°S～66°N)共确定了48 943个计算点(见图1(a))。数据长度自1992年10月～2012年4月，约19.5年。

月球白道面与地球赤道面之间的夹角称为月球赤纬角，最小为18.5°，最大为28.5°，两个极值的变化周期为18.61年，即为最长的分潮周期。为进行调和分析，取上述数据中最接近18.61年的长度(约18.609年)，即1992年10月3日～2011年4月29日，共685个cycle，每个星下点水位序列的时间间隔均为一个卫星重复周期9.915 6 d。由于三颗卫星在轨时间存在重叠，以重叠期均采用后一颗卫星数据的原则，本文具体选取的卫星数据如表1所示。

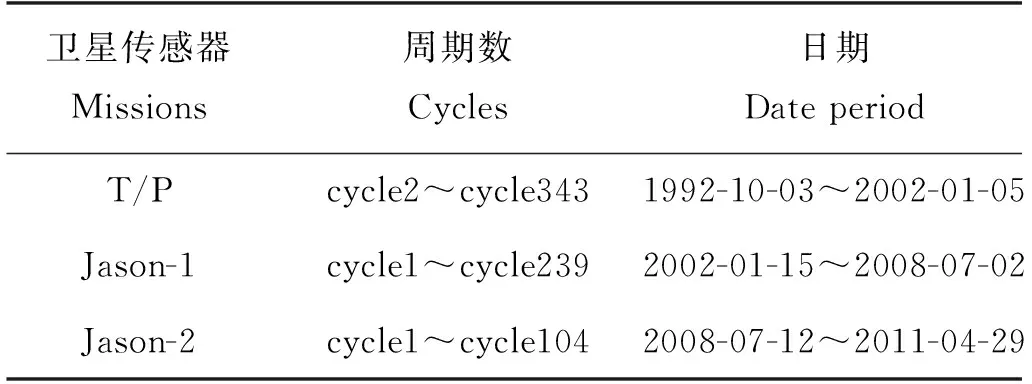
表1 本文使用的卫星数据Table 1 The satellite data used in this paper

1.2 验潮站数据

本文使用的验潮站数据取自夏威夷大学海平面中心(University of Hawaii Sea Level Center，以下简称UHSLC)提供的质控后逐时数据(Research Quality Data)。鉴于高度计数据时间跨度为1992-10-03～2011-04-29，本文从UHSLC提供的全部验潮站中筛选出了数据时间跨度能覆盖1992-10-03～2011-04-29的验潮站，对同样的18.61年数据进行调和分析，以排除不同时间跨度下可能的水深地形改变引起的潮汐特征变化。在66°N～66°S共有162个验潮站，其中水深超过200 m的有18个，水深在200 m之内的有144个。站位分布如图1(b)所示。

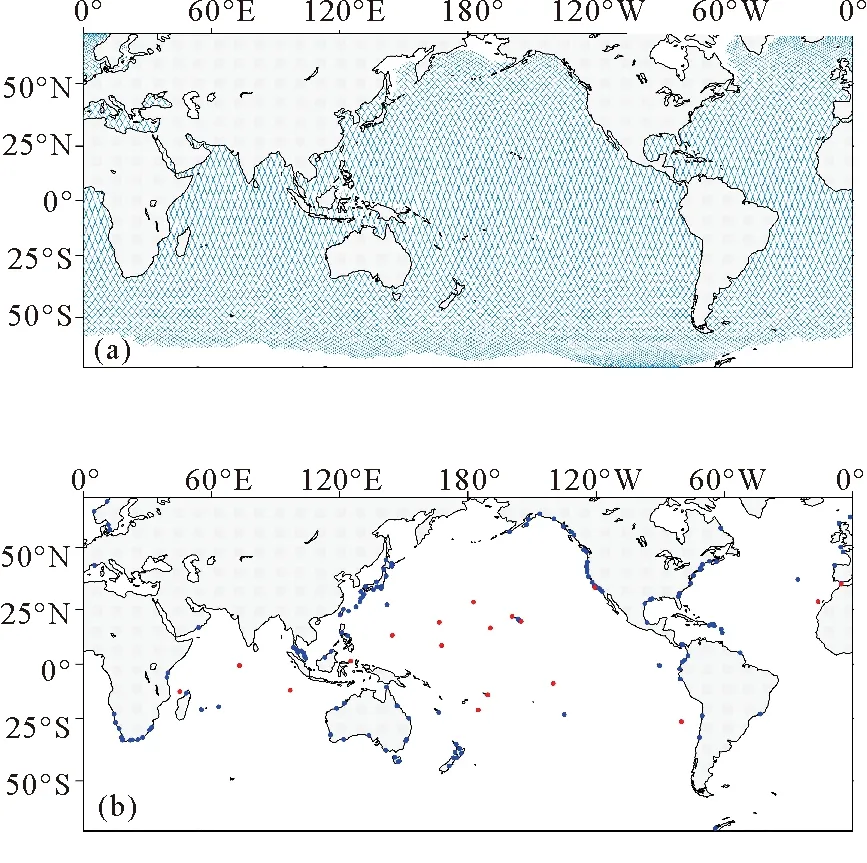
(红色圆点代表水深超过200 m的站位，蓝色圆点代表水深在200 m之内的站位。Red dots indicate stations with depth of over 200 m and blue dots indicate depth of within 200 m.)

1.3 TPXO9.1数据

本文在提取18.61年高度计资料的四大分潮同潮图时，作为佐证的是美国俄勒冈州立大学(Oregon State University)提供的TPXO9.1全球海洋模式输出的四大分潮调和常数结果。该模式基于拉普拉斯潮汐方程，除了对T/P系列高度计沿轨数据进行同化外，还包括高纬地区的ERS1,2/Envisat高度计沿轨数据和南北极测站数据[17]。其数据分辨率为1/6°，提供了8个主要分潮 (M2, S2, N2, K2, K1, O1, P1和Q1)、2个长周期分潮 (Mf, Mm)、3个浅水分潮 (M4, MS4, MN4) 及辐射潮S1和2N2共15个分潮的调和常数信息。

作为成熟的海洋潮汐模式，TPXO9.1在深海大洋中的M2分潮均方根误差仅为0.5 cm，在浅海及陆架处也仅3 cm左右，结果准确可靠，足以作为本文分析同潮图时的参照。尽管TPXO9.1中同化有T/P系列卫星高度计数据，但依然能在一定程度上佐证同潮图的准确性。

1.4 高度计资料的高频混淆

高频混淆是指卫星高度计对海表面高度进行离散采样时，频谱上形成虚假谱峰，高频信号向低频转移造成混乱的现象[18]。当采样间隔Δt给定时，能分辨出的最高频率，即折叠频率fN由(1)式给出

(1)

T/P系列卫星的取样间隔为9.915 6 d，远大于典型半日及全日潮的变化周期，故其相应的折叠频率也远低于典型分潮的频率。根据Rayleigh准则，分离两个不同频率的潮汐信号所需要的时间 T 应满足(2)式

(2)

式中F代表分潮周期。由此计算得到8个主要分潮基本分辨所需资料长度(见表2)。如表中下划线加粗字体所示，将M2和Q1，N2和O1分潮分辨开需要1.63年的资料，将M2和S2分潮分辨开需要2.97年的资料，而最长的分辨资料也不过是分离K2和P1所需的9.317年，其余分潮只需一年的资料就足够被分辨，远小于本文用于分析的18.61年。因此在使用18.61年高度计资料时无需考虑高频混淆的影响，使用超过2.97年的资料也足以将四大分潮(M2,S2,K1,O1)分离。

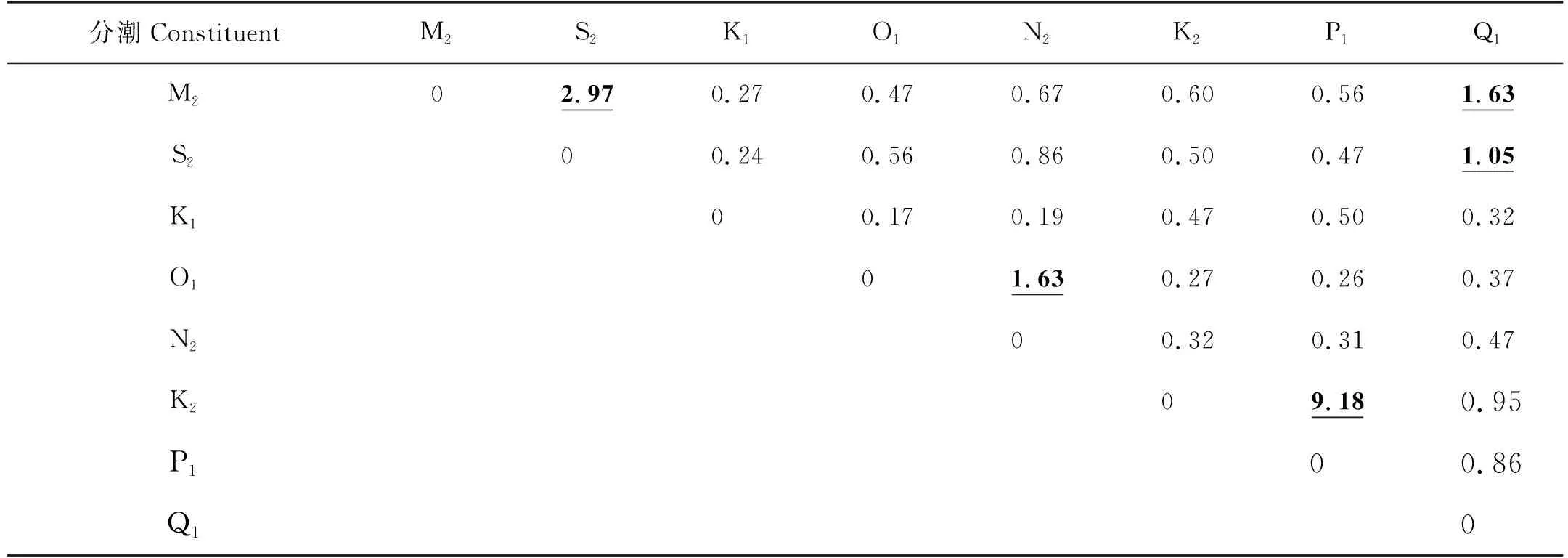
表2 8个主要分潮基本分辨所需资料长度Table 2 Alias synodic periods of each pair of 8 major constituents /a

2 结果分析与讨论

2.1 高度计分析结果准确性评估

2.1.1 与验潮站观测结果的综合比较 本文对上述计算区域(66°S～66°N)内48 943个计算点上18.61年的水位时间序列进行调和分析，得到68个分潮的潮汐调和常数；同样，对上述选取的计算区域内162个验潮站的水位资料分别进行调和分析，得到每个站位的调和常数。从中选取主要的半日分潮M2、S2和主要的全日分潮K1、O1，将高度计分析结果插值到上述站位，与验潮站观测结果进行了综合对比，以评估高度计分析结果的准确性。以下分别从调和常数的平均绝对偏差、绝对偏差范围及其百分比和矢量均方根误差三方面对不同分潮和不同水深进行讨论。

表3所示为四大分潮调和常数在全球海域及不同水深下的平均绝对偏差。在全球海域，四大分潮M2、S2、K1、O1的平均振幅偏差分别为6.91，2.60，1.39和1.05 cm。平均迟角偏差最大的是S2分潮，为16.27°；两个全日分潮的平均迟角偏差分别为10.28°和10.17°，较两个半日分潮低。从不同水深下的结果来看，水深大于200 m时结果明显优于水深小于200 m的结果。对于两个偏差相对较大的半日分潮来说，M2分潮在水深小于200 m时振幅偏差可达7.49 cm，而在水深大于200 m时振幅偏差仅有2.15 cm；S2分潮在水深小于200 m时迟角偏差达16.98°，而水深大于200 m时为10.50°，准确度也有着明显的提高。对于两个振幅较小的全日分潮，调和常数在水深超过200 m时也有改善，平均振幅偏差分别降低了1.36和0.27 cm，平均迟角偏差也分别有着1.86°和2.38°的降低。

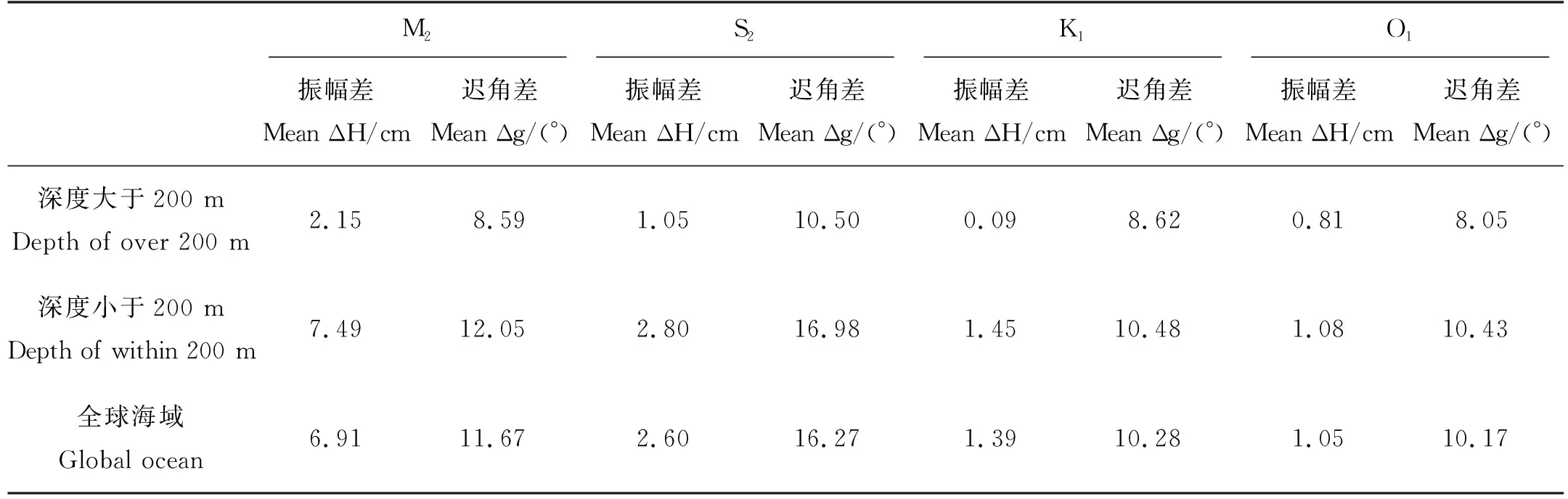
表3 调和常数平均绝对偏差Table 3 Mean absolute differences of the harmonic constants in different depth and global seas

高度计分析结果与验潮站观测结果的调和常数绝对偏差范围及其所占百分比见表4、5。由表4可知，对于S2、K1和O1分潮，振幅绝对偏差在2 cm之内的站点百分比分别为70.74%、75.61%及82.32%，对于M2分潮，也有超过60%的站点的振幅绝对误差小于4 cm。如表5所示，对于M2、K1和O1分潮，迟角绝对误差小于20°的站点均在90%左右，而对于上述提到平均迟角误差最大的S2分潮，迟角绝对误差小于20°的站点也超过了75%。

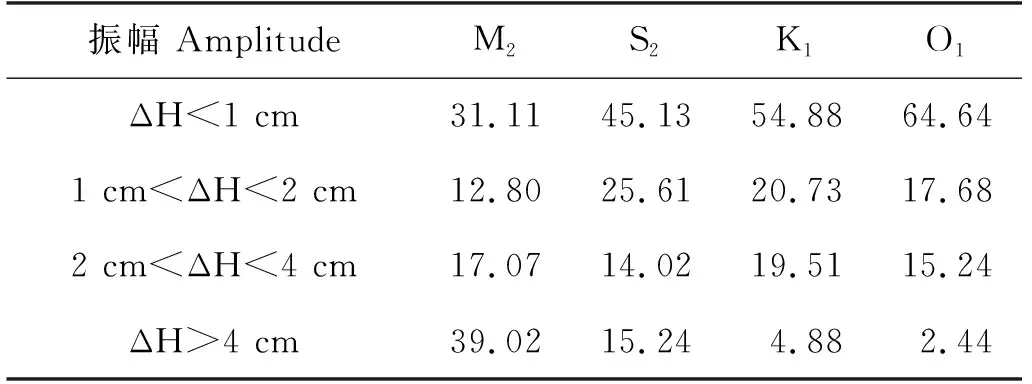
表4 四大分潮振幅绝对偏差范围及其所占百分比(%)Table 4 Distribution of the absolute differences of amplitude

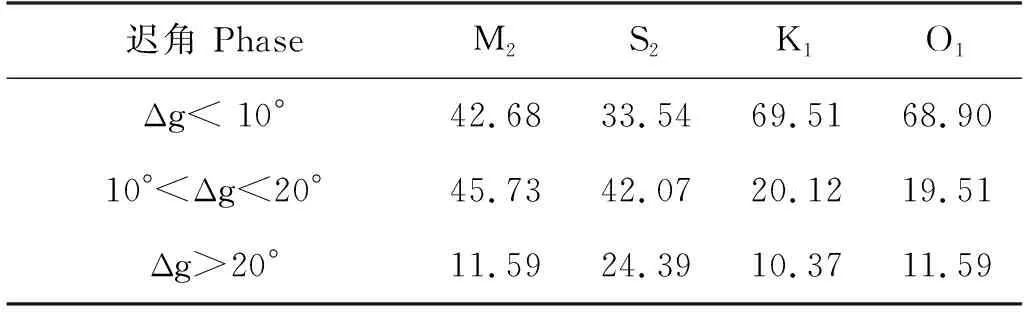
表5 四大分潮迟角绝对偏差范围及其所占百分比(%)Table 5 Distribution of the absolute differences of phase

为客观比较高度计分析结果及验潮站观测结果的偏差，表6给出了4个主要分潮调和常数在全球及不同水深的矢量均方根误差(Vectorroot mean square difference)。矢量均方根误差综合考虑了分潮振幅和迟角的误差，能更客观地评估各分潮调和常数的准确度。计算公式由Le Provost等[19]给出，如式(3)所示。其中T为分潮周期，N为验潮站个数

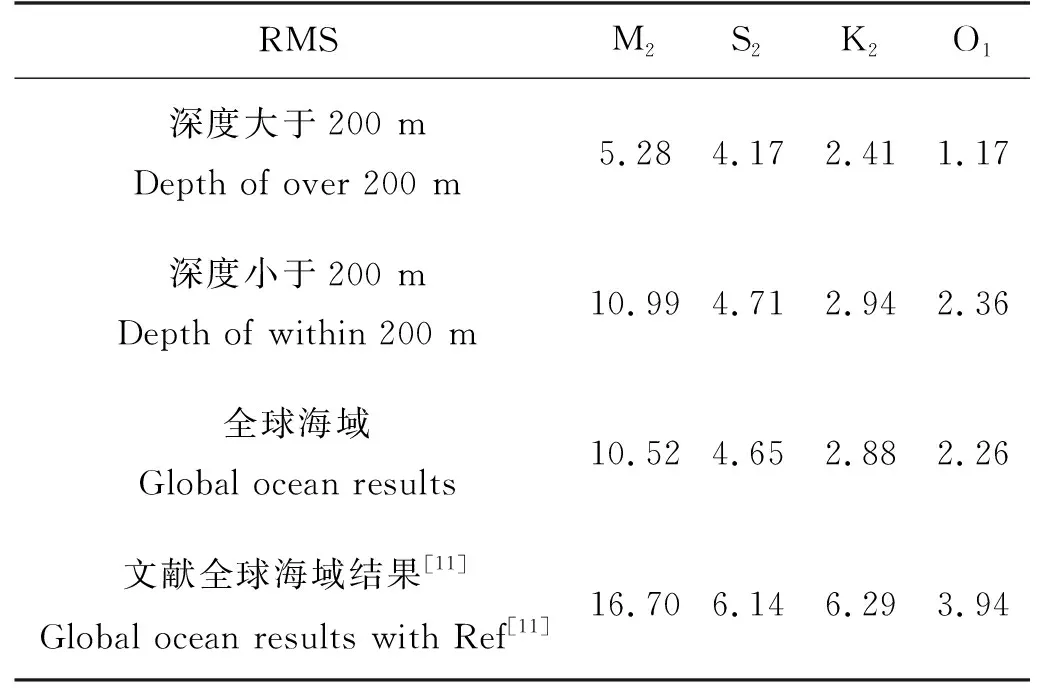
表6 四大分潮在全球及不同水深的矢量均方根误差Table 6 Vector RMS differences of four major constituents in different depth and global seas /cm

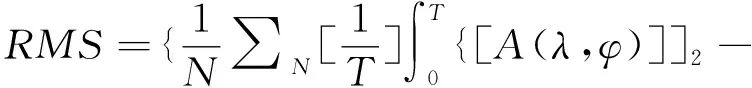
(3)

四大分潮在全球海域中的矢量均方根误差分别为10.52，4.65，2.88和2.26 cm，而沈春等[11]使用10年T/P资料得到的此误差为16.70，6.14，6.29和3.94 cm，本文四大分潮的准确度均优于其结果。另外M2分潮的矢量均方根误差最大，O1分潮最小，这一趋势也与其结果一致。从不同水深下的结果对比来看，卫星高度计资料在水深低于200 m的浅海及陆架处误差相对较大，最大的M2分潮矢量均方根误差接近11 cm；而水深超过200 m时，最大的M2分潮矢量均方根误差也不过5.28 cm，最小的O1分潮仅为1.17 cm，四个分潮的准确度比水深小于200 m时都有着提高。

综上，本文的高度计分析结果是可信的。虽然在浅水仍存在一定缺陷，但这是由地形和计算点的限制决定的。在浅海由于地形的影响，潮汐特征变化较快，轨道间隔在300 km左右的高度计卫星很难捕捉到精细的潮汐特征；另外，深水验潮站大多分布在开阔大洋中，而浅水验潮站大多位于岛屿及陆架附近，卫星高度计数据在岛屿附近不连续，数据平滑处理的结果准确度将弱于开阔大洋中的相应结果[5]。此外，验潮站观测资料中还包括陆架浅海处的边缘波及陆架波等现象引起的海面变化，而简单的资料分析方法还不能充分考虑这些影响[11]。

2.1.2 基于18.61年高度计资料的四大分潮同潮图 将上述高度计分析结果的调和常数插值到1°×1°的网格上进行四大分潮同潮图的绘制，并与全球海洋模式TPXO9.1的输出结果进行对比。

如图3所示，高度计分析结果中四大分潮的振幅与TPXO9.1相比，在大部分海域无明显差异，只是在加拿大东北侧近岸处高度计分析结果偏大。这是由于高度计卫星覆盖范围的限制，插值不能完全反映缺测处振幅的变化所致。对于M2分潮，最大振幅超过3.3 m，是所有分潮中振幅最大的一个；在赤道太平洋附近，印度洋中部和大西洋中部等中低纬海域存在超过0.5 m的振幅高值区。S2分潮的最大振幅在0.5 m左右，高值区的分布与M2分潮类似，只是赤道太平洋东侧的高值区范围较小。综合来看，对于半日分潮M2和S2，北半球东岸振幅整体大于西岸，而南半球相反。作为两个主要的全日分潮，K1分潮和O1分潮的振幅分布也同样相似，但K1分潮振幅相对较大，O1分潮在南半球高纬海域也另有高值区。两个全日分潮的振幅在北太平洋和印尼群岛附近较大，埃及半岛附近也有相对高值区。整体较之，两个全日分潮的振幅较两个半日分潮更小。由于地形的影响，各分潮振幅在近岸普遍大于深海大洋。旋转潮波系统的振幅在无潮点处最小，随着与无潮点距离的增加而变大。二者在四大分潮的旋转潮波系统个数及位置上也得到了基本一致的结果，特别是半日分潮M2和S2，而全日分潮K1和O1在南半球的同潮时线相对杂乱，无潮点位置不够清晰。本文认为这一现象是由于TPXO9.1提供的结果经过了八次平滑[17]，故插值结果的平滑度更优。另外，TPXO9.1的分辨率为1/6(°)，在计算区域内有170余万个数据点，同化过程中还引入了沿岸测站的结果，而本文使用的高度计数据只有48 943个计算点，且高度计数据在近岸存在一定误差。但总体来说，从18.61年高度计数据提取的同潮图有效地再现了四大分潮的全球分布特征，与TPXO9.1结果基本吻合，从而佐证了本文中高度计分析结果的可信度。

图2 18.61年四大分潮高度计分析结果((a)、(c)、(e)、(g))与TPXO9.1输出结果((b)、(d)、(f)、(h))的四大分潮同潮图Fig.2 Comparison of the co-tidal chart from harmonic analysis results of 18.61-year altimetry data((a),(c),(e),(g))and results of TPXO9.1 assimilation model((b),(d),(f),(h))

2.2 18.61年内M2分潮特征随时间的变化

根据表2，将M2分潮与其他主要分潮基本分辨所需的最长资料长度为与S2分潮分离开的2.97年。因此在分析M2分潮特征是否存在时间跨度上的变化时，本文选取了研究时段内最接近2.97年的数据(110个cycle，约2.988年)，即该18.61年内最初2.97年(1992-10-03～1995-09-18)和最末2.97年(2008-05-13～2011-04-29)，对两个时段内的资料分别进行分析，选取分析结果中M2分潮的调和常数，插值到1°×1°的网格上绘制同潮图，并将两个时段内的结果进行对比，以探究M2分潮特征在18.61年跨度上的变化，同时排除其他分潮的混淆影响。

如图3(a)中所示为两个时段内分析得到的M2分潮等振幅线，可见大部分海域振幅较为稳定，部分海域振幅有量值较小的变化。做差后进一步绘制图3(b)中两时段内的振幅变化，其中非洲大陆东南侧振幅略有增加，且由北向南的增加量逐渐增大，量值约0～5 cm，马达加斯加岛西侧振幅略有减小。孟加拉湾北部和格陵兰岛西侧振幅略有增加，量值不超过5 cm。在三个大洋中，太平洋海域中振幅产生变化的海域面积大于大西洋和印度洋，其中北太平洋尤甚。

(黑线代表最初2.97年分析结果，红线代表最终2.97年分析结果。Black contours show results from the first 2.97-year. Red contours show the last 2.97-year.)

在不考虑高度计卫星在近岸精度误差的前提下，聚焦中国近海，M2分潮振幅在此海域有一定变化。在渤海中，辽东湾振幅有明显的增加，莱州湾有明显降低，量值均在10 cm左右，这与孟云等[16]利用2004和2014年岸线地形数据进行模式验证的结论相似；而黄海北部靠近朝鲜半岛的海域振幅有10 cm左右的增加，山东半岛南侧有5 cm左右的增加，江苏沿岸有5 cm左右的降低；东海沿岸地区振幅增加，其中台湾海峡一带变化明显，量值同样在10 cm左右；同样，在南海沿岸，海南岛附近，振幅有5 cm左右的增加。

两个时段内的M2分潮的同潮时线见图4(a)。同样，同潮时线在三个大洋内随时间推移的变化并不显著。做差后进一步得到图4(b)中两时段内的迟角变化，可见迟角在全球大部分海域变化为0，较大的变化大多分布在无潮点附近。菲律宾海东侧有两个相距较近的无潮点，可能也在一定程度上加剧了这种偏差。日本海及周边海域变化较明显，在30°左右。泰国湾北部沿岸迟角也有30°左右的增加。另外，在南太平洋50°S～60°S海域及北太平洋25°N～50°N之间有呈轨道状分布的小幅度迟角变化，偏差大约在10°之内。在60°S以南的海域迟角也有较明显的变化，这可能与该处星下点相对密集，同潮时线不够平滑有关。

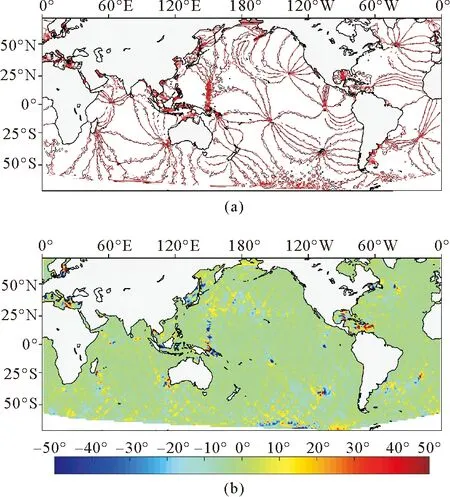
(黑线代表最初2.97年分析结果，红线代表最终2.97年分析结果。Black contours show results from the first 2.97-year. Red contours show the last 2.97-year.)

从上述比较中可以看到，在18.61年跨度上，大部分海域的调和常数变化不大，但在中国近海振幅变化可达10 cm；迟角变化大多分布在无潮点附近，这可能由于进行插值时，无潮点附近的周期性会造成巨大误差[13]。而日本海周边海域及泰国湾北侧也有30°左右的变化。图中呈轨道状分布的变化可能与T/P系列卫星轨道间隔和插值过程有关。当无潮点或振幅较高的区域处于两条轨道之间时，插值无法得到该区域的真实值。星下点的分布不均也可能导致插值过程不能完全反映调和常数的分布情况。

3 结语

本文基于三颗高度计卫星18.61年的沿轨数据在全球海域形成的48 943个不规则分布的计算点上进行了调和分析，得到以下结论：

系统对比162个与高度计数据时间跨度一致的验潮站观测结果，当水深大于200 m时，四大分潮的矢量均方根误差仅为5.28，4.17，2.41和1.17 cm，在大洋中的分析结果是真实可信的。虽然在浅水仍存在一定缺陷，但这是由地形和计算点的限制决定的。此外，本文分析结果的准确性较前人结果也有着明显提高。

对比高度计分析结果与TPXO9.1输出结果的同潮图，除去高度计覆盖范围和插值结果平滑的限制因素，四大分潮的振幅分布、旋转潮波系统个数及位置与TPXO9.1基本吻合，佐证了本文分析结果的准确性。

在此基础上，排除其他分潮的混淆影响，对比分析最初2.97年和最末2.97年资料中M2分潮的分析结果，发现在18.61年时间跨度上，大部分海域M2分潮的振幅和迟角的变化不大，但在中国近海振幅变化可达10 cm；迟角变化大多分布在无潮点附近，在日本海周边海域及泰国湾北侧则有30°左右的变化。

致谢：卫星遥感数据和验潮站数据分别来自宋箐阳博士和夏威夷大学海平面中心，TPXO9.1数据来自美国俄勒冈州立大学，在此一并致谢。