基于层次分析-熵权法的投资组合构造研究
霍潇潇,陈如赞
(华南农业大学工程学院,广州 516000)
0 引言
随着近年来我国经济跨越式的增长,证券交易制度系统的完善,推动证券交易市场的快速发展,越来越多个人投资证券市场,以获取收益。而市场价格的波动十分强烈,直接影响个人投资收益率及投资风险,所以对证券市场波动的规律性研究,分析引起市场波动成因,成为当下投资者进行投资决策关键,使个人投资更具有科学性。投资者选股投资最关心的是投资收益率及投资风险的大小,即“高收益,低风险”的最理想化投资方案,则投资者在选择投资策略时一般会权衡收益与风险的利弊,综合各方面考虑,得出最合理的投资方案。
本文选取部分股票作为一般研究对象,对数据集中个股计算累计收益、标准差,再进行归一化处理。通过构建所选取部分股的层次分析模型,对数据进行定性定量分析,通过主观定量选取收益与风险比例,且对一致性进行检验,得出投资比例。在层次分析模型计算结果的基础上结合熵权法,进一步权衡收益和风险,更加客观对投资权重进行修正。为了验证得到投资组合的正确性,我们在实验阶段使用夏普比率对投资组合进行评估。
1 数据预处理
我们所分析数据集中的各股指参数如图1所示。

图1 数据集中部分股票指标折线图
对数据进行预处理,股票日收益R t为:

股票累计收益R T:

为了减少投资管理成本,我们根据高收益低风险的原则,计算各股票的累计对数收益率和日收益率的标准差,根据2:1的比例粗略计算组合权重1。将各股数据代入计算,得到排序(取组合权重前10的股票),如表1所示。

表1 股票累计收益相关参数

图2 组合权重1的柱状图
2 使用层次分析法构造投资组合
筛选出前五名[1]股票进行分析。然后以收益率和风险率为指标,运用层次分析法对这五只股票做进一步的研究和分析。
层次结构一般分为三层,最上面为目标层,中间为准则层,最下面为方案层[2]。

图3 层次分析法示意图
首先构建准则层对目标层的成对比较矩阵:

再构建方案层对准则层的成对比较矩阵:

得到矩阵mij后进行归一化处理,得到归一化后的权重向量:

层次分析法需要对这个权重向量进行一致性检验,定义一致性指标C I为:

其中,λmax为判断矩阵m ij的最大特征值,RI为随机一致性系数,当C R小于0.1时,可认为通过一致性检验[3]。求解得CR=0.0836,通过单排序一致性检验。权重结果作为投资组合权重,如表2所示。

表2 投资组合权重
3 使用熵权法修正投资组合
熵值取权法在于通过判断各个因素的变化强烈程度来决定该因素在最终目标中所占的权重[4]。本文对层次分析法给出的权重矩阵W1,熵值取权法求出权重矩阵W2,两矩阵按照W1:W2=3:7的比例进行效正,从而给出最终4个因素对合理化指标的组合权重值矩阵,确定最终组合权重。
此处选取收益为正向指标、风险为负向指标,构建决策矩阵A:

对表1中已经归一化处理的数据,为了避免求熵时取对数无意义,需要进行数据平移:
正向指标平移:

负向指标平移:

然后计算第i个用户的第j个指标的比重y ij:

第j个指标的信息熵e j:

其中K为常数:

第j个指标的权重w j:

利用加权求和公式计算组合权重2(此处称为S):

将组合权重2与层次分析法求出的组合权重1按3:7进行组合,最终投资组合权重如表3所示。

表3 最终投资组合权重

图4 最终投资组合饼状图
4 投资组合评估
我们综合考虑收益和风险,采用夏普比率模型指标进行评估。夏普比率计算投资组合每承受一单位总风险,会产生多少的超额报酬,即衡量投资对象的“性价比”[5]。其公式如下:

其中,E(R P)为组合投资的回报率期望值;R f为无风险利率(一般为投资国债的回报率);σP为投资组合超额收益的标准差。
计算投资组合中五支股票对数回报率的平均值和标准方差,结果如表4所示。

表4 股票对数回报率平均值及标准方差
根据上表中数据计算投资回报率期望:

通过对国债回报率数据[6]查询得

计算投资组合协方差σAB:

其中,R为回报率;μ为期望回报率;P为出现概率,这里取1。协方差计算结果如表5所示。
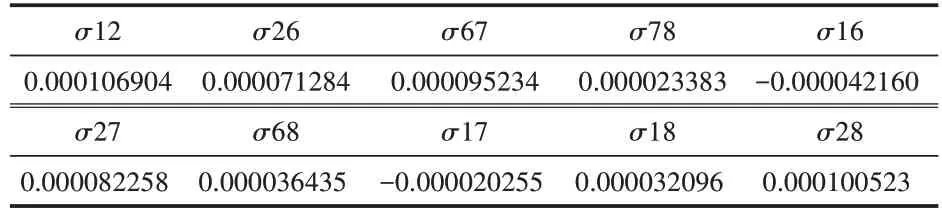
表5 投资组合协方差
投资组合超收益的标准差公式如下:
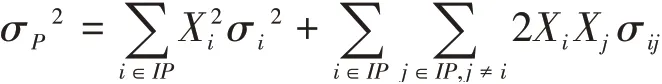
其中,σi为第i支股票的回报率的标准差;X i为第i支股票所占的比重;σij为回报率协方差。计算得σP12=0.000188714,σP1=0.0137373212。
最终得夏普比率为0.8837。
5 结语
本文研究了一种层次分析-熵权法模型用于投资组合构造。层次分析的思想在于不割断各个因素对结果的影响,而层次分析法中每一层的权重设置最后都会直接或间接影响到结果[7]。熵权法通过计算熵值来判断一个事件的随机性及无序程度,也可以用熵值来判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的权重越大[8]。两者综合可以得出一个更合理的权重。
在实际方案选择过程中,我们总是要综合收益与风险进行考量。层次分析法能够结合对于收益与风险的权重进行分析得出对股票投资的比重选择,得到一个系统的清晰的结果;熵权法对权重进行一个更加合理的调整。层次分析法不仅适用于存在不确定性和主观信息的情况,还允许以合乎逻辑的方式运用经验、洞察力和直觉[9]。层次本身能够衡量指标的相对重要性。所需定量的数据信息较少,能化为简单的权重进行计算。在层次分析法的基础上,再运用熵权法。熵权法充分利用了原始数据,利用决策矩阵求权进行客观赋权,优化了层次分析法过多的主观因素,使得模型更具可信度和精确度[10]。
但层次分析法缺乏各指标之间的横向比较,如相关性、层级关系等。若无业务经验指导,权重可能失真,对样本的依赖性较大,随着建模样本不断变化,权重会发生一定波动。这也是之后需要关注的问题。

