具备预判能力和向最小距离学习的粒子群算法

舒小丽，刘衍民，张倩

（1.贵州民族大学数据科学与信息工程学院，贵阳 550025；2.遵义师范学院数学学院，遵义 563006；3.贵州大学数学与统计学院，贵阳 550025）

0 引言

粒子群算法［1］（PSO）是模拟了鸟类在群体中的捕食行为，它将群体中的鸟看作是无质量的粒子，通过群体中粒子之间的相互合作和信息交流来寻找最佳食物的位置。由于粒子群算法相对简单，易于实现，且没有太多的控制参数需要调节。1995年由Kennedy和Eberhart正式提出以来，吸引了众多研究者对此进行研究。多次模拟实验结果显示，该算法对于解决大多数优化问题都有较好的优化效果。目前被应用于控制系统、预测时间、动态车辆路径以及其他算法领域。但是，PSO算法在复杂的多峰问题上还存在多样性差、易早熟收敛、精度低等一系列问题，为了解决这些问题，提升算法的运行效果，研究者们提出了许多该算法的改进。①参数改进：Kennedy等［2］人在1998年提出了线性惯性权重因子，改进了早期粒子群算法收敛性慢的问题；②拓扑结构：根据拓扑结构的不同对粒子群算法进行改进，比较经典的是分为局部的拓扑结构和全局拓扑结构，它们的差异是学习样本的选择不同，该方法对于不同的问题表现出不同的优化效果；③多群粒子群算法：VAN［3］和刘衍民［4］将种群分为多个种群，由种群之间信息共享，提高算法的运行效率，它们与原始的粒子群算法相比性能有显著提高。

本文在研究者研究的基础上，结合SHI［2］和张津源［5］提出了具备预判能力和向最小距离学习的粒子群算法。该算法中首先粒子根据每个粒子的个体极值对自己下一代的寻优做一个预判；其次，粒子的社会部分学习对象是从预判的方向上选取最小距离，这些策略可很大程度上提高粒子的寻优精度。

1 标准的粒子群算法

标准的粒子群算法与最先提出的粒子群算法相比，前者在速度更新时的记忆项中多了一个惯性权重，即w。w的大小影响着粒子的搜寻能力。当w较大时，具有很好的全局搜寻能力，而局部搜寻能力较弱；当w较小时，局部搜寻能力较强，全局搜寻能力较弱。因此，选择合适的w值有助于平衡PSO算法的全局寻化能力和局部寻优化能力。PSO算法的速度和位置更新方程如下：

其中，a1、a2为学习因子；r1、r2为［0,1］中均匀分布的参数；Pit表示粒子i在寻优过程中时刻t经历的最佳位置，称为粒子的“自我认知项”。Gt表示寻优过程中群体在时刻t经历的最好位置，称为粒子的“群体认知项”，也称为社会学习部分。

2 具备预判能力和向最小距离学习的粒子群算法

2.1 预判

在寻优过程中，PSO算法的粒子根据式（1）和式（2）更新其速度和位置。由于粒子在寻优过程中受个体极值和群体最优的整体指导，使得对粒子的每一维度过程的关注极少，特别在复杂的多峰问题上。又由于粒子在寻优过程中产生很大的随机性，使得粒子收敛到最佳位置更加艰难。比如在群体寻优过程中：粒子刚开始运动的方向是向着群体最优解的方向前进的，但由于寻优过程的复杂性和随机性，在进行到某代时可能会偏离最优解的方向，如若继续使用式（1）更新速度，由于上一代错误信息的指导，必将导致收敛速度慢、精度不高等问题。

为解决这个问题，粒子在下一次更新迭代时会进行一个预判，即通过监督粒子在进化过程中的运动方向以及运动位置，对下一代实施干预，以防被错误信息指导。本文的预判策略是：首先规定个体极值的维度为正时是该维度较好的方向，反之，故粒子在下一次寻优时对各个粒子的个体极值每一维度进行预判，对维度为正的，则不改变方向，对维度为负的则改变该维度的方向。即面对个体极值中维度较差的方向时，则向反方向寻优。面对个体极值中维度较好的方向时，寻优方向不变。

2.2 具备预判能力和向最小距离学习的粒子群算法（MDPSO）

当前的研究者所做的研究中，种群速度更新的社会部分都采用了整个维度的更新策略。但在面对复杂的多维函数优化问题时，该方法可能会因为维间的相互干扰导致某些正确的寻优维度的信息被掩盖。从文献［3］推断出，如果每个粒子速度更新都向群体最优学习，将会造成“steps foward，one step back”的现象。虽然下一代的函数值更好了，但可能有的维度信息比上一代更差了，这造成了好的维度信息的丢失。

根据粒子群算法的特点，个体极值既然是粒子历史过程中经历的最好的位置，并且全局最优也是从个体极值中挑选出来的，那么每个粒子的个体极值中都隐藏着较好的解的信息。又因为每个粒子的个体极值各不相同，在寻优时为群体提供了多种选择。在以上实施预判的基础上，粒子从每个粒子的个体极值中逐一挑选距离最小值作为粒子在该维度的学习对象。在每一维度都确定后，就组成了一个新的维度，称为“最小距离”，用Z表示。由于新的Z是从每个个体极值的每一维度挑选出最小距离组成的。故该策略能有效的提高算法的寻优速度。新的学习策略速度更新如下：

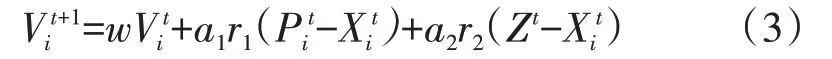
2.3 MDPSO算法流程

MDPSO算法在寻优过程中，每个粒子根据个体极值与最小距离Z调整其飞行方向，并逐步逼近最优解。

（1）初始化种群，设置a1、a2和w，并计算其适应值。

（2）粒子实施预判，确保向正确的方向飞行，并找出Z。

（3）使用式（3）、式（2）更新粒子的速度与位置。

（4）更新个体极值和全局最优。每次迭代后，如果粒子当前位置的适应值小于该粒子历史最佳位置的适应值，则用当前的位置更新个体极值，否则不更新；如果粒子当前位置的适应值小于群体最优位置的适应值，则用当前位置更新群体最优位置，否则不更新。

（5）如果没有达到给定阈值，则返回（2），反之，算法结束。群体最优位置即是全局最优解。

2.4 算法的复杂性分析

为了研究MDPSO算法复杂度是否比PSO算法的更加复杂，用T表示最大的迭代次数，po p表示种群规模，D表示粒子的维数，MDPSO算法在PSO算法的基础上给粒子增加了一个预判行为，并对算法中社会部分的学习做了调整。其中MDPSO算法的复杂度计算为K1=O（po p×D×T），PSO算法的复杂度计算为k2=O（pop×D×T）。由于K1=K2，故从以上的推导可得MDPSO算法与PSO算法的复杂度相比并无差别。

3 实验设置与讨论

3.1 检测函数和算法的参数设置

本文选择CEC2017年版中的检测函数，具体如下：

Sum-of-different-power（F1），Zakharov（F2），High-condition-elliptic（F3），Ackley（F4），Rastrgin（F5），Expanded-sxhaffer-F6（F6），Bent-cigar（F7），Schaffer-f7（F8），Non-continypus-rataed-rastrigin（F9），Griewank（F10），并将MDPSO算法与5种具有代表性的改进PSO算法进行比较，这些算法分别 是：PSO1［2］、UPSO［6］、CLPSO［7］、CPSO［2］和wFIPS［8］。

为了使各算法的实验结果对比显著，本文实验的相关数据设置如下：种群规模都为30，各算法在每个检测函数上独立运行30次，每个检测函数每次运行6×104次函数评价，其他实验相关参数与算法在提出时一致。

3.2 实验结果及分析

3.2.1 收敛特性

为了展现各算法在上述参数设置下的收敛特性，图1给出了这些算法在6×104次函数评价后的收敛特征曲线图。

同时，为了检验各种算法运行结果之间的差异是否具有统计学意义，采用Wilcoxon秩和检验对MDPSO算法得到的结果与其他五种改进PSO算法中最好的一组结果进行检验。表1右侧给出了检验结果。其中h=1表示运行结果有差异，h=0表示运行结果没有差异。

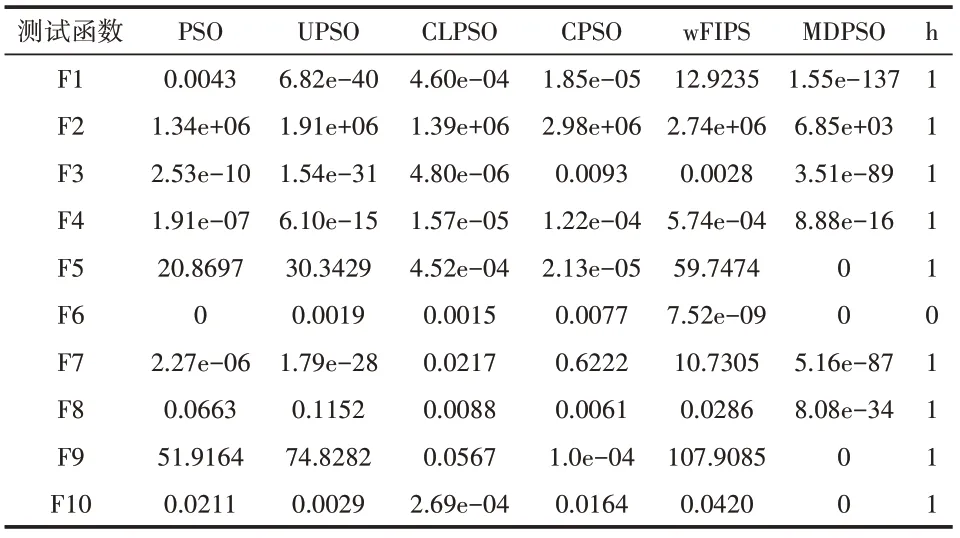
表1 各算法实验对比结果（平均值）

从表1和表2可以看出，本文提出的MDPSO算法在10个检测函数上的性能表现相比其他5种PSO算法更加优秀。其中在函数F1、F3、F7、F8上表现较为明显，函数的均值与其他的各种算法中最好的结果分别降低了97、58、59和30个数量级，说明MDPSO算法在改善粒子群的寻优能力较为显著，在规避早熟问题上更加具有优势。

表2 各算法实验对比结果（最小值）

表1右侧给出了Wilcoxon秩和检验结果分析。除F6外，其余5种改进的PSO算法中最好结果集与MDPSO算法的结果集的数据差异在95%置信区间内具有统计学意义。

从图1可以看出，除Ackley函数外，MDPSO算法在逐渐寻优过程中取得了最好的运行效果。尤其对于Zakharov，Schaffer-f7从一开始就表现出明显的优势。这主要是预判行为找出了食物在每个维度上的较好方向，指导粒子向好的方向飞行，使粒子更容易找到较好的解。

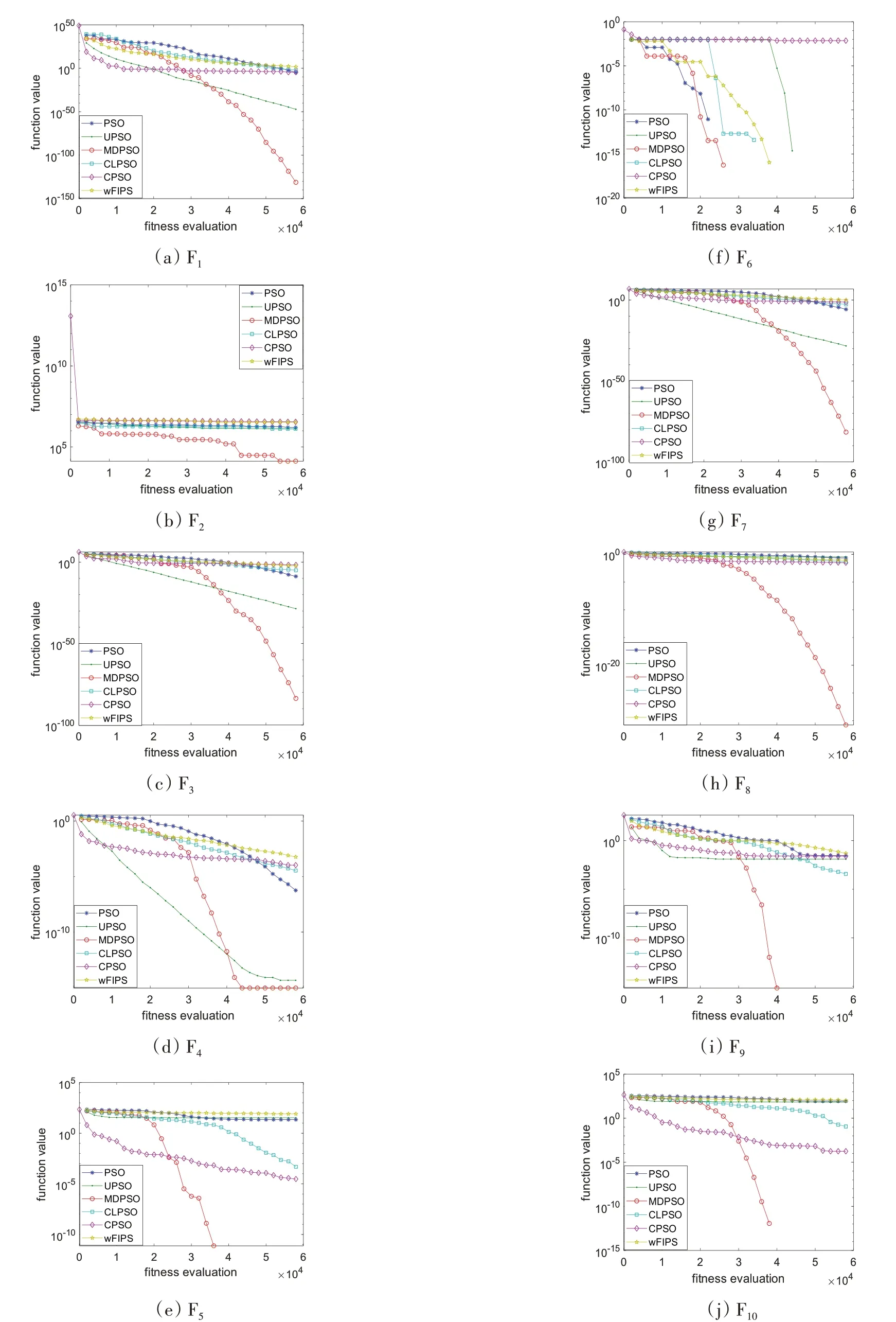
图1 检测函数收敛特征图

3.2.2 鲁棒性分析

为了测试各种改进的PSO算法在不同的函数上运行是否具有稳定性，选择了3个单峰函数（Zakharov，High-condition-elliptic和Ackley）和3个多峰函数（Bent-cigar，Schaffer-f7和Griewank）。根据表1与表2的数据可以看出，wFIPS与其他算法相比效果不明显。所以表3给出了MDPSO与4种算法独立运行60次的鲁棒性分析结果，其中“FES”表示在算法达到给定阈值时的函数评价次数，“S”表示算法达到给定阈值的比例（单位：100%），各函数的阈值分别为1.81e+06、3.95e-04、3.7e-05、0.095、0.05和7.1e-05。

从表3可以看出：在单峰检测函数中，对于Zakharov函数，仅仅只有MDPSO算法达到了给定阈值的比例是100%，但PSO和CLPSO也显示了其较为稳定。对于Expanded-sxhaffer-F6函数，UPSO和MDPSO达到给定阈值的比例是100%，但MDPSO运用了较少的函数评价，另外PSO和CLPSO也显示了其较为稳定。对于Ackley函数，PSO和MDPSO达到阈值的比例是100%，UPSO和CLPSO也显示了其稳定性。在3个多峰函数中，仅仅只有MDPSO达到阈值的比例是100%。但UPSO在Bent-cigar也表现其稳定性，且CLPSO和CPSO在Schaffer-f7也表现了其稳定性。

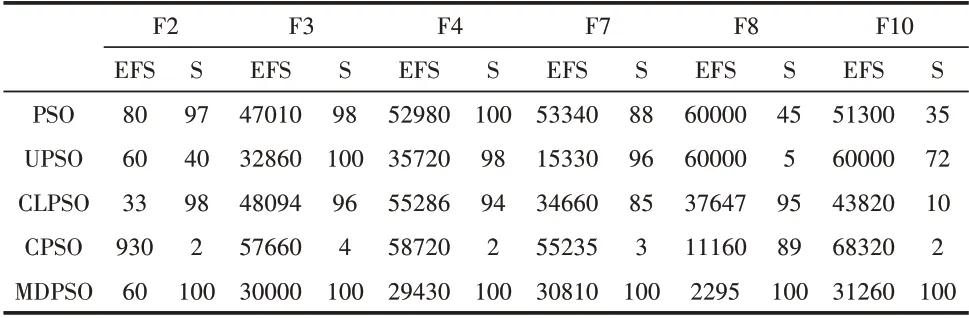
表3 各种算法的鲁棒性分析

从以上可知，不管从算法的收敛特性、寻优能力还是从算法的鲁棒性分析结果看，MDPSO算法都表现出一定的优势。

4 结语

为了解决由于PSO算法寻优过程中的随机性和在更新时对粒子的整体指导而导致粒子在寻优过程中易早熟收敛、精度不高等问题。本文提出了MDPSO算法。该算法是由粒子预判出较好方向，再从个体极值中提取每个粒子的有效信息指导粒子的社会部分学习。并通过Wilcoxon秩和检验和基准函数寻优实验表明，该算法不管在单峰函数还是多峰函数相比其他算法都表现出一定有效性和优越性。因此，MDPSO算法可以作为求解多峰和单峰问题的一种有效的方法。