基于嵌套−伪预估器反馈的时滞控制系统输入时滞补偿
刘青松
近几十年以来,时滞控制系统的分析与设计一直是一个比较活跃的研究课题,涌现了大量的研究成果[1−6].镇定和稳定性是时滞控制系统的基本设计问题,得到了深入的研究[7−9].镇定问题近年来得到了众多学者的重视.例如,文献[10]利用序贯预估器方法研究具有时变时滞的控制系统的镇定问题.针对具有输入时滞的关联系统,文献[11]利用基于分布式预估器的控制器解决了其镇定问题.文献[12]和文献[13]分别利用时滞相关脉冲控制方法和连续预估器方法研究(具有状态、输入和输出时滞)的控制系统的镇定问题.近年以来,针对时滞系统的稳定性涌现大量的成果.例如,文献[14−18]研究了时滞脉冲系统的(指数)稳定性.基于预估器反馈的方法,文献[19−20]研究了线性时滞控制系统的(鲁棒)稳定性.通过加权不等式的方法,文献[21]研究了具有时变时滞离散系统的有限稳定性.文献[22]给出了线性中立型时滞系统指数稳定性的必要条件.
预估器反馈方法已经广泛应用于时滞控制系统的分析与设计中,学者们对其进行了深入研究.例如,文献[23]首次提出Smith 预估器方法对输入时滞进行补偿,使得闭环系统变成无时滞系统.文献[24]采用预估器反馈方法考虑了具有多输入时滞的非线性系统的镇定问题.针对具有随机网络时滞的网络化控制系统,文献[25]利用网络预测控制方法分析其随机稳定性问题.从频域的角度,文献[26]研究了时滞控制系统的设计问题,提出了有限谱配置方法.最近,文献[27]提出一种称为伪预估器反馈的新方法,研究仅含输入时滞的线性系统镇定问题.不同于传统的预估器反馈利用开环系统预测系统未来的状态,伪预估器反馈则是利用闭环系统预测系统未来的状态,从而所得到的控制器是无记忆的或者是有限维的.后来,伪预估器反馈方法[27]推广到了含有多个点时滞与分布输入时滞的线性系统[28]和输入时滞与状态时滞相同的线性系统[29].此外,文献[30]还提出了另一种称为截断预估器反馈方法.
最近,针对同时具有输入和状态时滞的控制系统,文献[31]提出一种称为嵌套预估器反馈的新方法,研究大输入时滞补偿问题.这种方法随后推广到了同时具有输入和状态时滞的中立型时滞系统[32].几乎在同一时间,文献[33]采用基于开环系统基础解矩阵这一完全不同的方法,独立地研究了此问题.文献[33]中的方法也推广到了中立型时滞系统[34].
受文献[27]针对仅含输入时滞的滞后型线性系统所提出的伪预估器反馈方法和嵌套预估器反馈方法[31]的启发.本文针对同时具有输入和状态时滞的线性系统,通过建立嵌套−伪预估器反馈这一新方法,研究仅对其输入时滞进行补偿的控制系统设计问题.与传统的模型化简理论或有限谱配置理论不同,本文不是对输入和状态时滞都进行补偿(即保证闭环系统具有有限个特征值),而是仅对其输入时滞进行补偿,使得补偿后的系统仅含有状态时滞,而且状态时滞的大小不会增大.本文主要贡献如下:1)提出了嵌套−伪预估器反馈这一新方法.2)针对同时具有输入和状态时滞的线性系统,基于嵌套预估器反馈的控制器在实现时,需要增加输入滤波器才能镇定原时滞系统[31−32].本文提出的基于嵌套−伪预估器反馈的控制器无需增加滤波器便可镇定原系统.3)文献[27]研究仅含输入时滞的线性系统的输入时滞补偿问题,本文研究同时具有输入和状态时滞的线性系统的输入时滞补偿问题.此外,伪预估器反馈方法不能直接应用于同时具有输入和状态时滞的线性系统中,因为基于伪预估器的控制器含有未来的状态而不可实现(输入时滞大于状态时滞).
1 问题描述
考虑同时具有输入和状态时滞的中立型控制系统

其中,A∈Rn×n和B∈Rn×m都是定常矩阵,假设矩阵D∈Rn×n是舒尔稳定的,r >0和h>0 分别表示状态时滞和输入时滞.不失一般性地假设
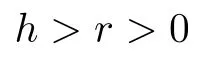
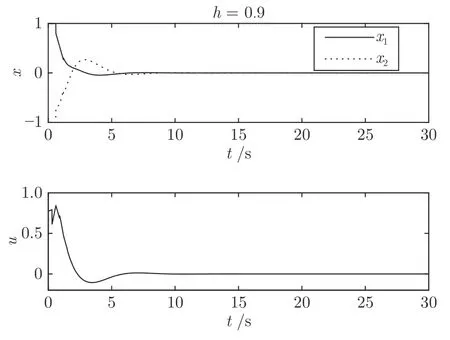
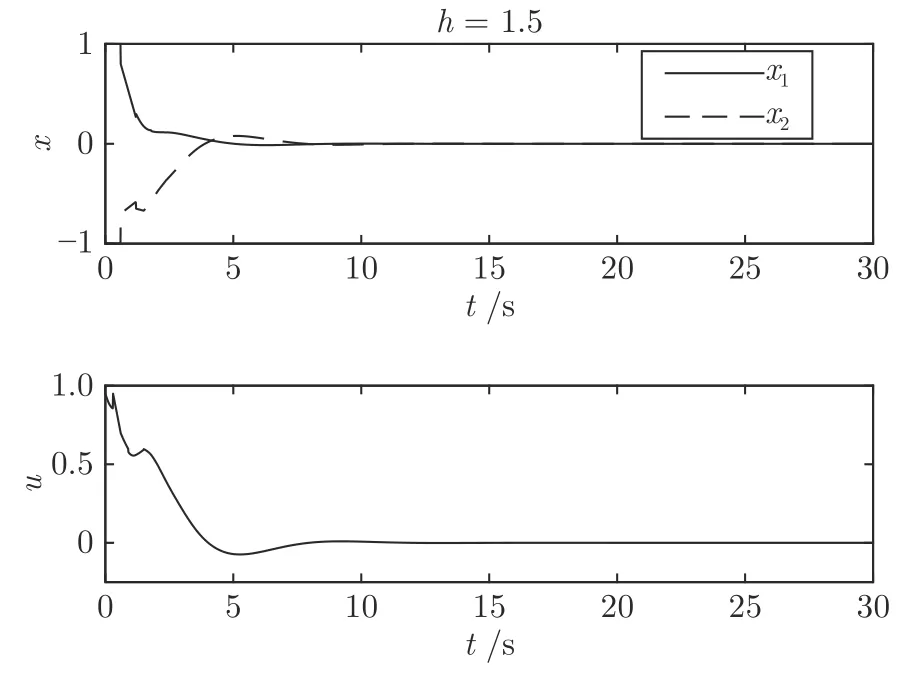
而当 0 问题 1.针对时滞控制系统(1),设计一个线性控制器 使得闭环系统是渐近稳定的,其中,F 是线性泛函,xt(t)=x(t+θ),θ ∈[−r,0].类似文献[31],给出下列假设. 假设 1.存在反馈增益矩阵K∈Rm×n,使得下列时滞系统是渐近稳定的 因此,问题1 等价于寻找一个适当的方法补偿输入时滞.针对同时具有输入和状态时滞的线性系统,模型化简方法可以处理这样的镇定问题,然而,此方法需解一个由系数矩阵组成的非线性矩阵方程[35].最近,文献[33]采用基于开环系统的基础解矩阵方法研究了问题1,同时文献[32]也研究了问题1.然而,所设计的控制器都含有下列积分项[32,34] 需通过数值积分进行实现.而数值积分的缺点是无论数值积分多么精确,闭环系统可能都不稳定[36].文献[32,34]通过增加输入滤波器解决了控制器的实现问题.本文将给出一个完全不同的解决方案,既解决了传统预估器反馈控制器的实现问题,也克服了嵌套预估器在数值实现时闭环系统可能不稳定问题(需增加输入滤波器). 注意到,时滞系统(1)与控制器 组成的闭环系统 与式(2)的形式一样,则由假设1 可知,闭环系统是渐近稳定的.但是,由于控制器(5)含有未来的状态x(t+h−r),h>r,需利用系统的模型对其进行预测.当h>r时,由于基于传统预估器的控制器仍然含有未来的状态而不能实现,且含有类似于式(4)的积分项,故传统预估器反馈方法不再适用.由文献[31]和[27]可知,嵌套预估器反馈[31]和伪预估器反馈[27]方法都可预测状态x(t+h−r) 的值.基于嵌套预估器反馈的控制器也含有类似于式(4)的积分项而不易数值实现.故利用伪预估器反馈[27]的思想,结合闭环系统(6),可得 其中,Ac=A+BK.注意到,如果h>2r,预估器(7) 仍然含有未来状态x(t+s) ,s>0,而不可实现.结合文献[31],本文将建立嵌套−伪预估器反馈方法.主要思想如下:利用闭环系统(6)可先预测x(t+θ1),θ1∈[0,r],即 上面预估器是可实现的.显然地,对任意的h−r >0,存在唯一的非负整数κ使得h−r ∈(kr,(k+1)r].因此,可得到状态x(t+s) ,s∈(0,h−r] 的预测值.则控制器(5)可重写为 此控制器是可实现的.控制器(10)是由伪预估器(9)以状态时滞r为步长嵌套地得到的,故控制器(10)称为嵌套−伪预估器反馈控制器. 注意到,控制器(10)含有多重积分,虽然不影响控制器实现,但形式较为复杂.为此,下面给出仅含一重积分的显式嵌套−伪预估器反馈控制器.根据文献[32]可得 其中,φ(t)=x(t)−Dx(t−r),fk(·),gk(·) 和ςk(·)递归地定义为 初值为f0(·)=In,g0(·)=In和ς0(·)=Ac. 则可得下面引理,其证明与文献[32]中定理2 证明类似. 引理 1.设存在非负整数κ和θh∈(0,r],使得κr+θh=h.则控制器(10)可写为 其中,fκ(·),gκ(·) 和ςκ(·) 由式(11)所定义. 注意到,引理1 给出了仅含一重积分的显式嵌套-伪预估器反馈控制器. 本节将给出系统(1)和(12)组成闭环系统的稳定性分析.注意到,闭环系统可写为 根据文献[32]定义一组矩阵函数如下: pk+1,k+1(δ)=In,qk+1,k(δ)=In,δ=σ−σ0,其中,j ∈I[0,k]:={0,1,···,k}和l∈I[0,k−1],初值为 下面定理将给出保证由式(1)和(12)组成闭环系统稳定的充要条件. 定理1.在假设1 成立的条件下,令存在非负整数κ和θh∈[0,r] ,使得κr+θh=h.则由式(1)和(12)组成闭环系统是渐近稳定的当且仅当下面积分时滞系统是渐近稳定的. 其中,ξ(ϑ,θ0)=pκ−1−i,j(ϑ)Bϱ(t+θ0),ζ(ϑ,θ0)=qκ−1−i,l(ϑ)Bϱ(t+θ0),ϑ=θh−θ0,pκ,j(·),qκ,l(·)由式(14)和(15)所定义. 证明.注意到,闭环系统(13)可重写为 其中 注意到系统(17)与文献[32]中的系统(1)具有类似的结构.根据引理1 和文献[32]中定理2 的证明,可得 其中,fκ(·),gκ(·),ςκ(·),pκ,j(·) 和qκ,l(·) 由式(11),(14)和式(15)所定义.则将式(19)代入式(18)可得积分时滞系统 (16).因此,如果积分时滞系统(16) 是渐近稳定的,则由式(17) 可得,式(1) 和(12)组成的闭环系统是渐近稳定的.必要性易得,故省略. 通过把多重积分转化为累次积分,易知积分时滞系统(16)与文献[27]中式(17)具有类似的形式.故可利用文献[27]中保证积分时滞系统(17)稳定的充分条件分析积分时滞系统(16)的稳定性. 由定理1 可知,基于嵌套−伪预估器反馈方法事实上解决了同时具有输入和状态时滞的中立型时滞系统的镇定问题.与传统预估器反馈和嵌套预估器反馈[31−32]相比,嵌套−伪预估器反馈不含有类似于式(4)的积分项.故嵌套−伪预估器反馈控制器优点是,在数值实现时,无需输入滤波器便可镇定原时滞控制系统.此外,嵌套−伪预估器反馈方法还可以推广到更一般的中立型时滞控制系统. 其中,Ai∈Rn×n,i∈I[0,n1] 和Bj∈Rn×mj,j ∈I[0,n2]为定常矩阵,0=r0≤r1≤···≤rn1和0=h0≤h1≤···≤hn2分别是状态时滞和输入时滞. 本节将嵌套−伪预估器反馈方法推广到滞后型时滞系统.令D=0,则系统(1)变为下面滞后型时滞控制系统. 则闭环系统(6)退化成 嵌套−预估器(8)和(9)分别退化成 和 由于嵌套−伪预估器(22)与文献[37]中式(8)具有类似的结构.则可得未来状态值(t+kr+θk+1) 为 其中,对所有的i∈I[0,k−1], 和Fk+1,k(θ)=Fk,k(θ),Fk+1,k+1(θ)=AcFk,k(θ). 式(24)的初值条件为F0,0=Ac和G0=In. 设存在非负整数κ和θh∈[0,r],使得κr+θh=h.由式(23)可得显式的嵌套-伪预估器反馈控制器为 下面推论将给出保证闭环系统渐近稳定的充分必要条件. 推论1.假设存在增益矩阵K,使得系统(21)是渐近稳定的.设存在非负正整数κ和θh∈[0,r] 使得κr+θh=h.则式(20)和(25)组成的闭环系统是渐近稳定的当且仅当下列积分时滞系统是渐近稳定的. 证明.由式(20)和(25)组成的闭环系统可写为 其中 注意到式(27)与文献[37]中的式(1)具有相似的形式.因此,通过引理1[37],可得 其中,Fκ+1,i(·) 和Gκ+1(·) 由式(24)所定义.则将式(29)代入式(28)可得系统(26).因此,如果系统(26) 是渐近稳定的,由式(27) 易知,式(20) 和(25)组成的闭环系统是渐近稳定的.必要性易证,故省略.□ 值得注意的是积分时滞系统(26)的稳定性分析可参考文献[38].事实上,本节利用嵌套−伪预估器反馈方法,解决了同时具有输入和状态时滞的滞后型线性系统的镇定问题.本文所提出的方法由第2 节的中立型时滞系统推广到第3 节的滞后型时滞系统是非平凡的,例如定理1 中的充要条件(16)不能直接退化到推论1 的式(26). 考虑同时具有输入和状态时滞的线性系统[39] 其中,系数矩阵为 B=[0,1]T,状态时滞r=0.6. 为了更好地说明本文所提方法的有效性,分别地取三个不同的输入时滞h=0.9,h=1.5和h=2.设计状态反馈增益矩阵K使得λ(A+BK)={−0.75,−0.8},从而得到 1)h=0:9 根据等式κr+θh=h,可得κ=1和θh=0.3.下面将利用本文提出的嵌套−伪预估器反馈控制器补偿输入时滞.由引理1 可知,嵌套−伪预估器反馈控制器设计为 2)h=1:5 根据等式κr+θh=h,可得κ=2和θh=0.3. 由引理1 可知,嵌套−伪预估器反馈控制器设计为 3)h=2 根据等式κr+θh=h,可得κ=3和θh=0.2. 嵌套−伪预估器反馈控制器设计为 令初值为x(0)=[1,−1]T.则系统(30)分别与嵌套−伪预估器反馈控制器(31),(32)和(33)组成闭环统的状态轨迹和控制信号如图1,图2 和图3所示,易知闭环系统是渐近稳定的. 图1 系统(30)和(31)组成闭环系统的状态轨迹和控制信号Fig.1 State trajectories and control signals for the closed-loop system consisting of (30) and (31) 图2 系统(30)和(32)组成闭环系统的状态轨迹和控制信号Fig.2 State trajectories and control signals for the closed-loop system consisting of (30) and (32) 图3 系统(30)和(33)组成闭环系统的状态轨迹和控制信号Fig.3 State trajectories and control signals for the closed-loop system consisting of (30) and (33) 针对同时具有输入和状态时滞的中立型/滞后型时滞控制系统,研究仅对其输入时滞补偿问题,提出了嵌套−伪预估器反馈方法,不同于传统的预估器反馈利用开环系统预测系统未来的状态,嵌套-伪预估器反馈则是利用闭环系统嵌套地预测系统未来的状态,实现对任意大但有界的输入时滞进行完全补偿.结果表明闭环系统是渐近稳定的当且仅当积分时滞系统是渐近稳定的.最后,给出一个数值仿真验证所提出方法的有效性.
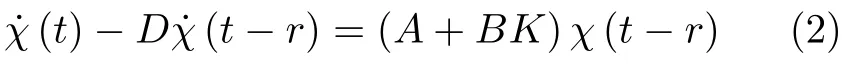
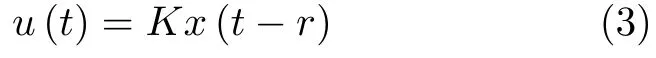
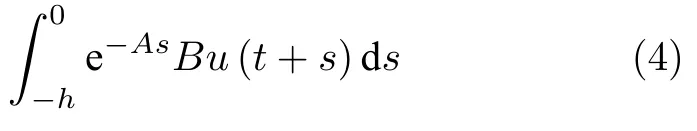
2 嵌套−伪预估器反馈
2.1 嵌套−伪预估器反馈的设计
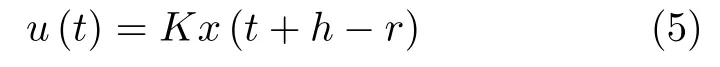

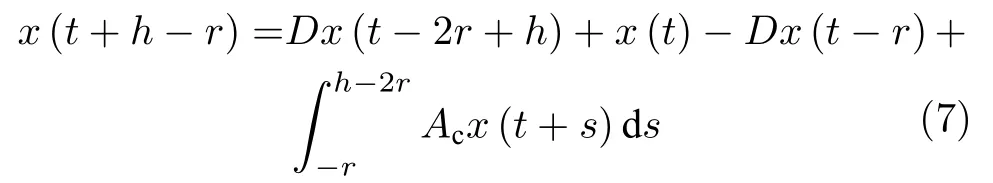
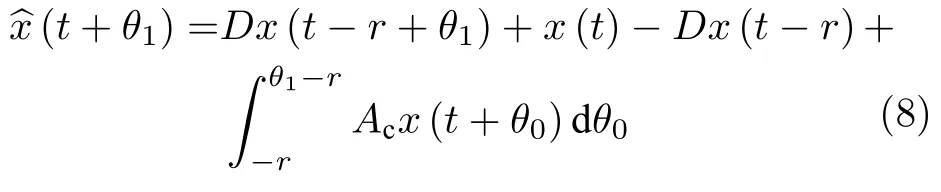
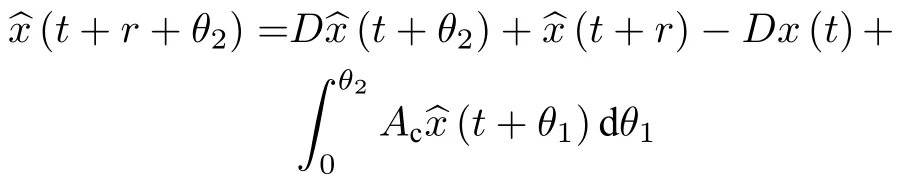
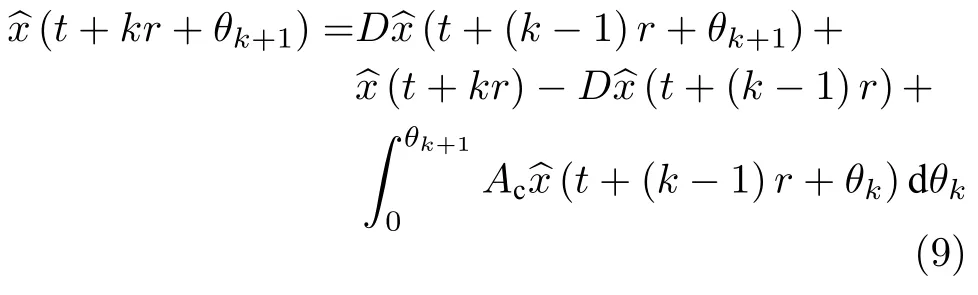
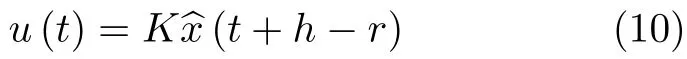
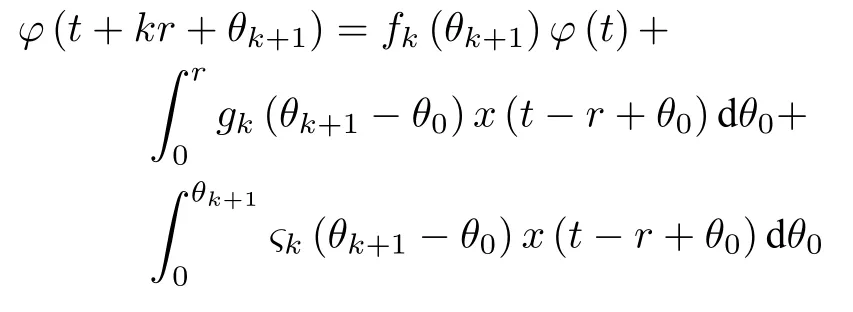
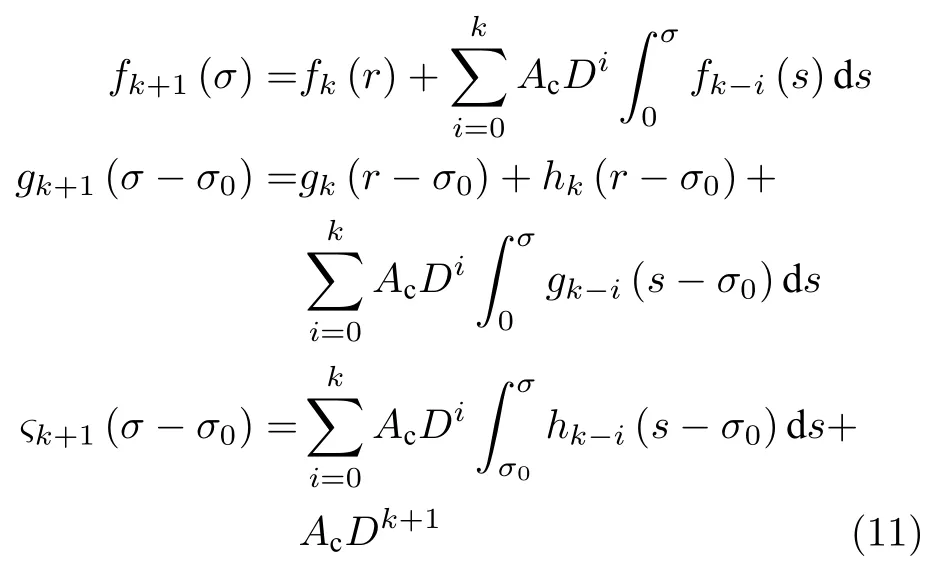
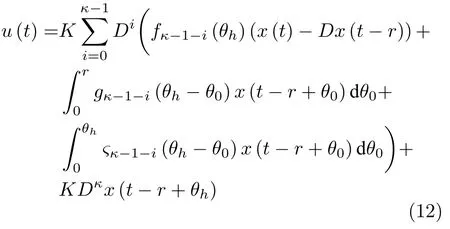
2.2 闭环系统的稳定性分析

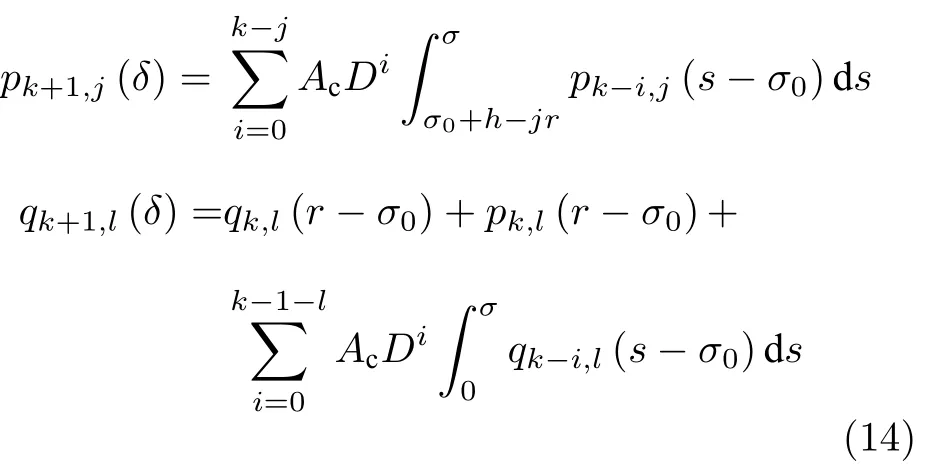
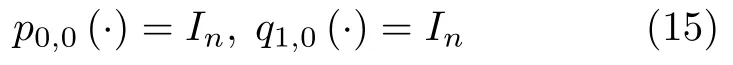
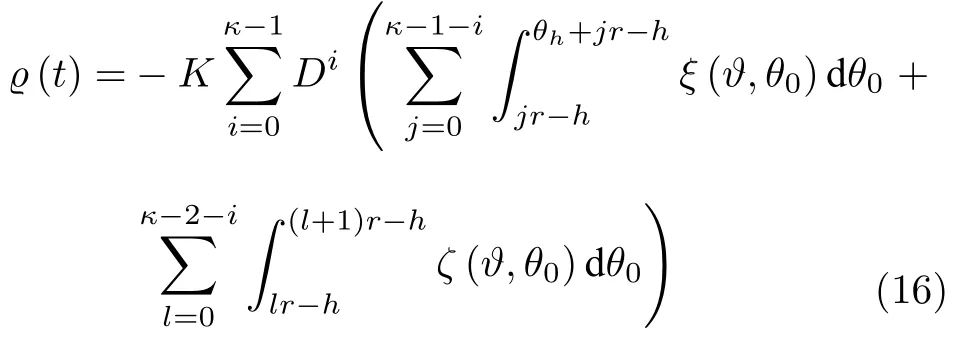
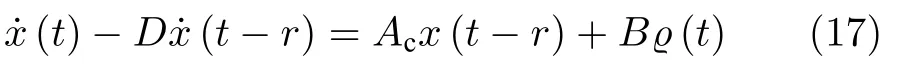
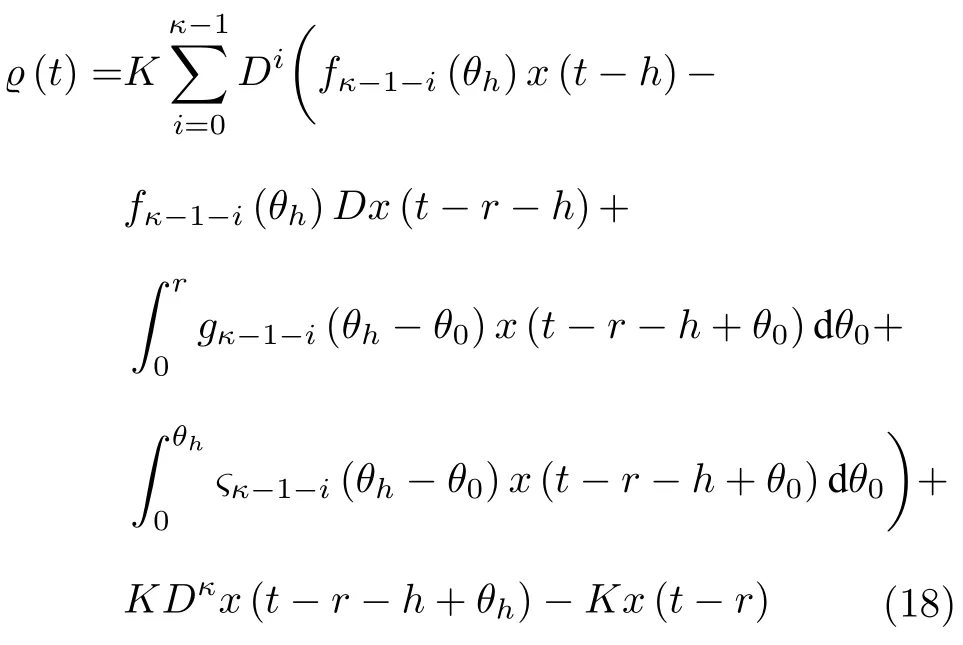
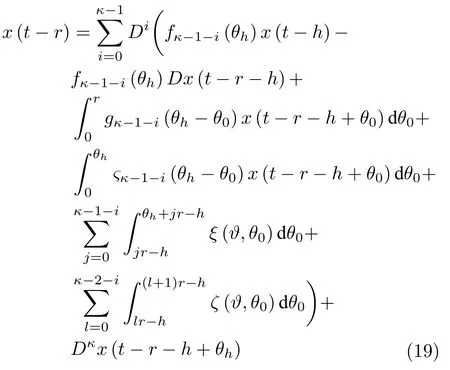

3 滞后型时滞控制系统

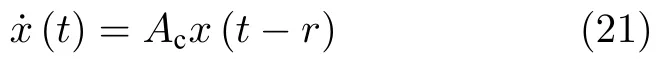
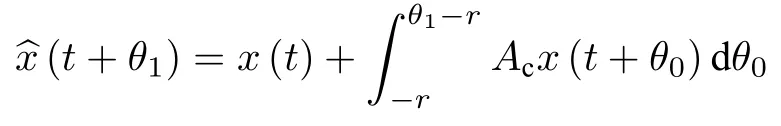
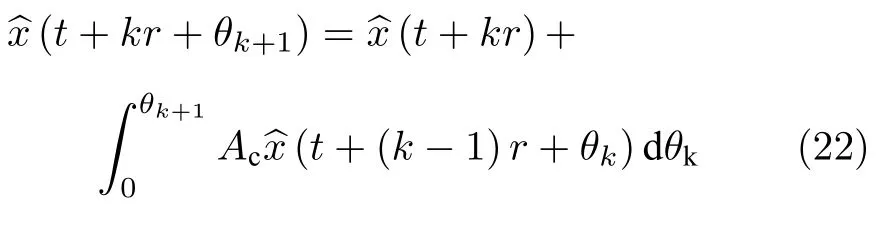
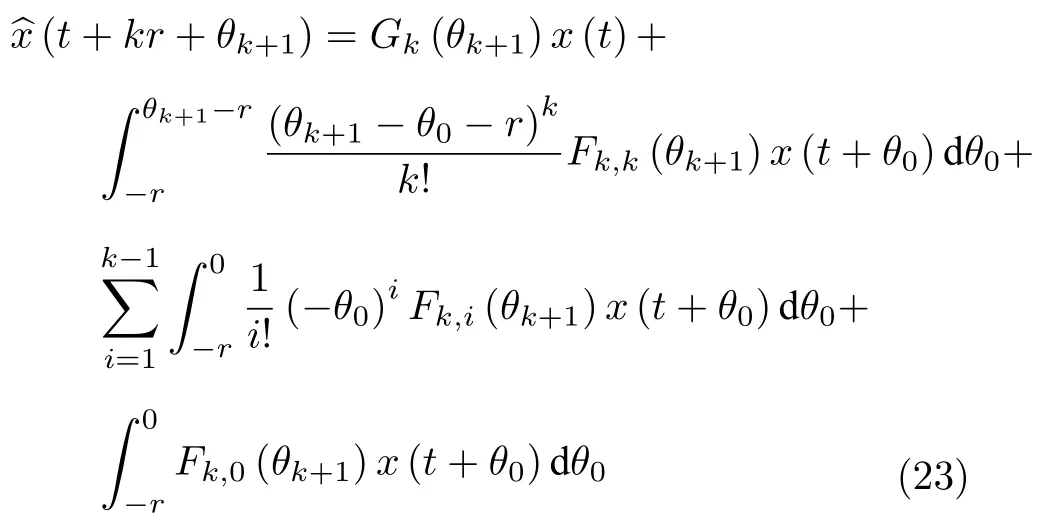
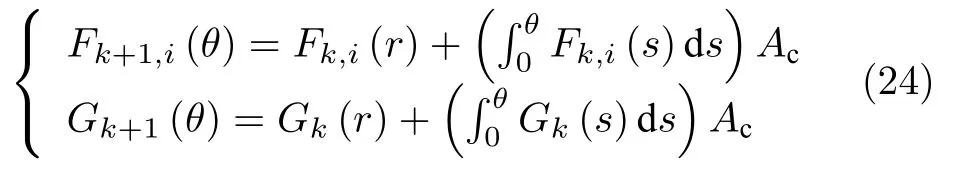
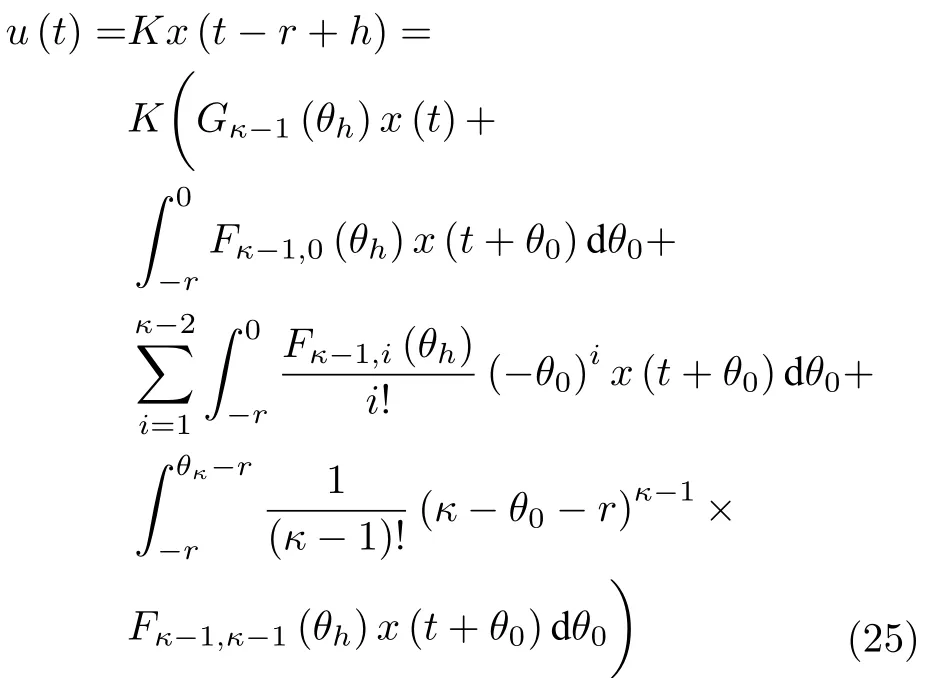



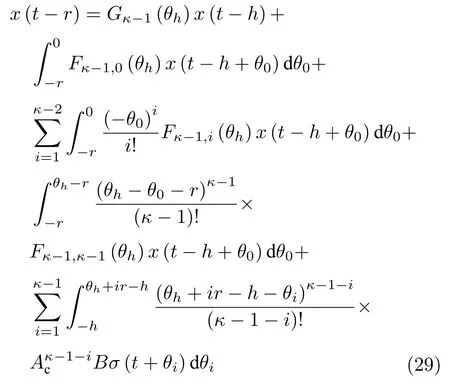
4 数值仿真
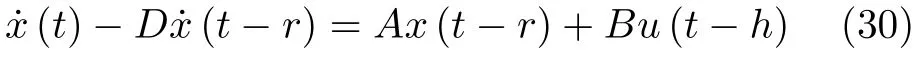

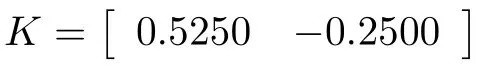
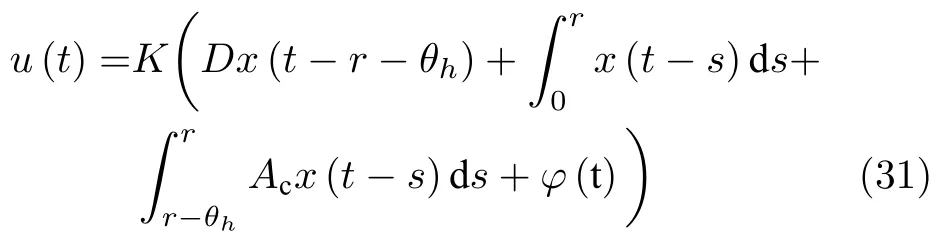
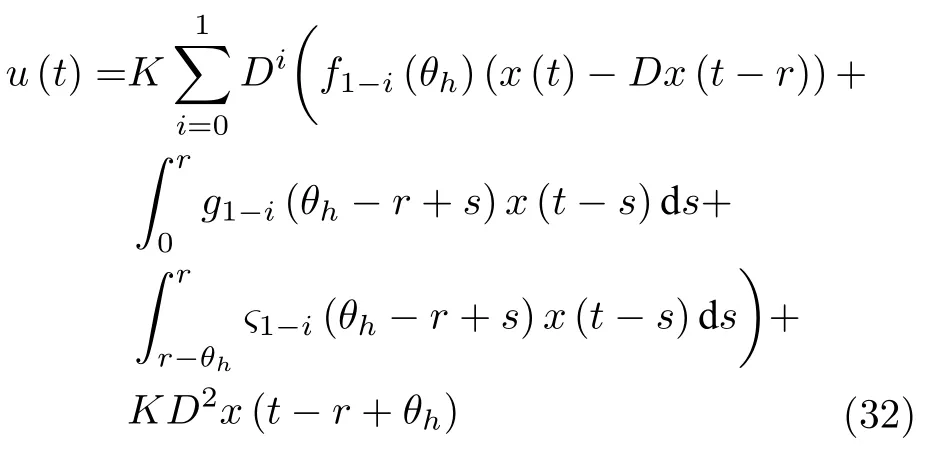
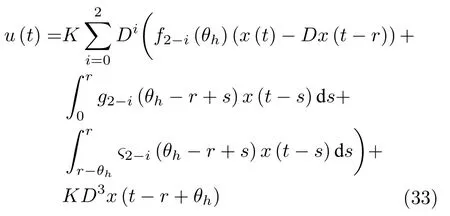

5 结论

