讲好学生的“故事”，提升运算能力的着力点——以一道函数求值题的教学为例

□钱大林 叶立军

（1.严州中学新安江校区，浙江建德 311600；2.杭州师范大学经亨颐教育学院，浙江杭州 311121）

运算能力是高中生应该具备的一种重要能力，也是数学运算核心素养中的关键内容.在运算方面，学生的“故事”就是运算思维的具体呈现，是对运算对象的理解过程，也是对运算法则的使用和展开过程.要讲好学生运算方面的“故事”，就是要讲好优秀运算思路的形成过程；就是要通过驱动性“问题链”，帮助学生自主辨析、独立思考的过程；就是要发掘运算成果的“因子”，调动学生参与运算的积极性，培养数学运算素养的过程.当前针对数学运算方面问题的讲评，缺少“对焦”学生的“真学情”“真水平”，忽视学生思维发生、发展的“故事”，难以实现从“知其然”到“何由以知其所以然”的理性思维的跨越.下面笔者以一道函数求值题的教学为例，立足讲好学生的“故事”，从教学准备、教学实施及教学思考三方面谈谈经验.

一、教材及学情分析

（一）教材分析

本节课是人教A 版（2019）普通高中教科书《数学》必修第一册第二章第三节《二次函数与一元二次方程、不等式》的习题课.主要展示一道有关高次多项式函数的拓展探索题的解题过程.这既是对二次函数学习的巩固，又是对一元二次函数学习的拓展迁移，还能对后续内容（其他的函数、方程以及不等式）的学习起到承上启下的作用.目的是让学生在确保解答正确的基础上，对代数式进行变形转化，简化运算，提升运算能力.

（二）学情分析

在本节课教学前，学生已经会解答类题：已知f(x)=ax2+bx+c(a<0)，其中a，b，c为常数. 若f(-1)=f(3)=0，解不等式：bx2+cx+a>0.学生能指出该题中“-1，3 是关于x的方程f(x)=0 的两个根”，并且得到f(x)=a(x+1)(x-3)，从而获得原不等式的解集.学生初步有了通过“同构式”去构造函数的活动体验.当把问题拓展到四次多项式函数，并考查学生的直观想象、逻辑推理、数学运算等核心素养时，笔者发现学生仅停留于代入消元的解题层次，对整体代换以及利用“同构式”去构造新函数的方法则使不上劲.检测结果显示该题的难度系数为0.21左右，学生的表现比预期要差许多.

（三）教学目标

1.能依据代数式的具体特征，合理变形转化，优化运算方法.

2.借助一道函数求值题的解题过程，体会问题解决的化归思想和函数方程思想.

（四）教学重、难点

重点：运用“基本量”表示和利用“同构式”构造函数两种方法求函数值.

难点：理解并掌握利用“同构式”构造函数的方法求函数值.

二、教学实施

（一）问题驱动，引发学生深度思考

教学说明：通过审题发现，本题需要打通两个节点：第一，如何破解只提供三个方程四个未知数的方程组问题；第二，如何从二次多项式函数的交点式迁移到四次多项式函数的交点式，实现快速求值.通过问题驱动，引发学生深度思考.

（二）特值导引，探寻运算路径

问题2根据“问题1”中学生得到的间接条件（1）（2）（3），如何求64a+16b+4c+2d的值？

问题3我们总得有理由，为什么可以令a=0？类比之下，我们是否也可以令a，b，c，d四个量当中任何一个为特殊值0 或1？如令b=1，请大家动手试试，结果又是如何?

通过计算，学生发现结果仍然为16.

教学说明：“道而弗牵，强而弗抑，开而弗达.”即教师要创设问题情境，通过追问，启发学生积极思考，让学生自主发现解题的线索，决不把最终结果端出来.在本题中，就是如何设定基本量、探寻降元路径，帮助学生突破“四个未知数，只有三个方程”的认知难点.

（三）设定基本量，探寻降元路径

问题5请大家思考上述两种不同的运算方法，你能发现这两种运算路径存在着的某种联系吗？

学生经过比较后发现：令a=0 的求值依据隐藏在步骤中.因此，用a，b，c等基本量表示是一条普适性的运算路径.

教学说明：从特值代入，到为了降元设定基本量“a”，学生领悟到了a，b，c，d任意三个未知量均可以用第四个量来表示的理性认识.设定基本量可以让所有的元素都联系起来，实现了化简求值的目的.如此，可让学生的思维从具体理性走向一般理性.

（四）整体代换，力求整体化解决问题

问题6本题的求值运算，你还有补充的方法吗？

问题7在尝试解决问题时，如果我们能联想到更为简单的类题，可以说离成功就不远了.大家动手试一试，看看能否绝处逢生？

教学说明：学生领悟了用新的基本量f(1)，f(2)，f(3)表示目标式的合理性，巩固并提升了学生用基本量进行多元表征的能力.

（五）关注结构，探寻同构化路径

问题8请大家观察下面两组函数值，你能用一个等式来概括它们吗？

（1）若f(1)=1，f(2)=2，f(3)=3，则f(x)=_______________.

（2）若f(1)=10，f(2)=20，f(3)=30，则f(x)=______________.

学生理解了题意，并分别写出：

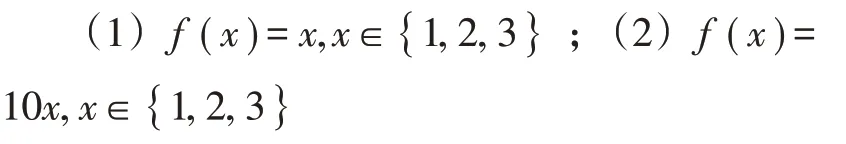
问题9等式f(x)=10x,x∈{ 1 ,2,3 }，好像在说什么话，大家能否换一种新的表达方式？

学生回答：1，2，3分别是关于x方程“同构式”的三个不同实根.

问题10这一新的具体发现有何利用价值呢？

通过启发并类比了一元二次函数的交点式，令f(x)-10x=(x-1)(x-2)(x-3)(xt)（t为方程的第四个根），则f(x)=(x-1)(x-2)(x-3)(x-t)+10x，所 以f(4)=64-6t，f(0)=6t，代入得：原式=16.

教学说明：教师可以顺势揭示这些奇妙构思的源头，是基于相同结构的式子f(1)=10，f(2)=20，f(3)=30，我们称之为“同构式”，并指出利用“同构式”构造函数的方法有利于解答一些复杂的问题.

（六）拓展思考，学以致用

问题11设f(x)=x4+ax3+bx2+cx+d，其中a，b，c，d为常数.如果f(-1)=f(3)=0，则9(a+b)-3c+5d的值为_________.

学生都能很快地理解题意，从同构的角度，指出“-1，3 是关于x的方程f(x)=0 的两个根”.于是将高次的代数式分解为两个低次代数式的乘积，即x4+ax3+bx2+cx+d=(x2-2x-3)(x2+mx+n)(m,n∈ R)，展开后比较系数得a=m-2,b=n-2m-3，c=-2n-3m，d=-3n，达到了a，b，c，d都用基本量m，n表示的目的，解得9(a+b)-3c+5d=-45.

教学说明：教师应该至少有一两次不仅要教会学生怎样更简便地解题，还要指出如何能从答案本身中去找出指向一个更简便解法的线索[1].关注过程教学，坚持学为中心、自然生成[2]、学用结合的教学思路，有利于调动学生积极参与运算的热情.

三、教学反思

（一）为什么要讲好学生的“故事”

涉及学生现实问题的“故事”的学习一定是生动的学习.本节课通过引导学生求值运算思路发生、发展的“故事”，帮助学生亲历了运算对象f(4)+f(0)的理解过程，使其运算思路经历特值代入—基本量表示—整体化处理—同构化构造的优化过程，生动、自然地化解了学生的学习困难，帮助学生领悟了数学算理，较好地提升了学生的数学运算能力.

（二）讲好学生的什么“故事”

在数学运算方面，学生的“故事”就是学生对一个个运算对象和算理的理解过程，是学生对一个个运算法则使用的过程，也是学生对一个个运算思维进行优化的过程.本节课以运用“基本量”表示和利用“同构式”构造函数两种方法求函数值的学习为主线，以领悟化归思想和函数方程思想为暗线，讲了学生运算思维自然发生、发展的“故事”，学习了有关“基本量”表示和利用“同构式”构造函数的新方法，化解了学生在理解运算方法上的受阻点，突破了学生在求异思维上的理解难点，以帮助学生养成一丝不苟、严谨求实的运算习惯.

（三）怎么讲好学生的“故事”

讲好学生的“故事”，首先教师需要创设合适的教学情境，让学生在情境中理解数学概念和运算法则，感悟数学命题的构建过程，感悟问题的本原和数学表达的意义[3].数学中的数与式，因其符号的抽象性、概括性，往往给学生带来比较大的“距离”感.本节课立足于学生的真实问题情境，为了把握方程组所蕴含的数学意义，从教学开始就顺应“特值代入”的求值思路，经历从具体到抽象、从特殊到一般的思维过程，帮助学生领悟“变形转化”背后的方程思想.

其次，遵循“最近发展区”的原理，创设驱动性“问题链”.创设驱动性“问题链”，能有效激发学生参与数学运算的热情.本节课通过“问题4”，帮助学生初步掌握了“基本量”表示的策略，即目标式64a+16b+4c+2d既可以用a（或b，c）等基本量表示，又可以用f(1)，f(2)，f(3)等基本量表示，深刻体会“基本量”法是数学运算中一条普适性的路径.

再次，要发掘学生的成果“因子”，调动学生参与运算的积极性.针对解题技能和数学思想方法的教学，不能急于求成.教师要有足够的耐心，给足学生思考的时间和空间.本节课，笔者从顺应学生“特值代入”的思路开始，当学生在“想”与“算”的环节上有不完整甚至错误时，仍然肯定学生思维的成果“因子”，并且留足时间，通过追问，循序渐进地帮助学生抽象、概括“基本量”表示和利用“同构式”构造函数求值的方法.学生则用心、用情体验了一系列运算思路的自然发现过程，感悟了运算路径的自然加工过程、优秀运算思路的自然生成过程.由此，笔者也顺利调动了广大学生参与运算的积极性.

学生的“故事”是鲜活的、宝贵的教学资源.教师应讲好学生的“故事”，立足学生的真实问题情境，循着学生的思维发生、发展，诊断学生对运算对象的理解过程、运算思路的选择优化过程、错误思维的纠偏过程，帮助学生经历“想”与“算”的过程，深入理解算理，走出认知困境，形成数学思想和方法，让数学运算成为学生的基本学习能力.