基于贝叶斯模型平均法和逐步回归法构建杉木单木胸径生长模型*

鲁乐乐 王 震 张雄清 张建国

(1.中国林业科学研究院林业研究所 国家林业和草原局林木培育重点实验室 北京100091；2.南京林业大学南方现代林业协同创新中心 南京210037)

单木胸径是估算立木材积、评价森林生产力的重要基础因子(Lhotkaetal.， 2011)。影响单木胸径生长变化的因子很多，如气候、立地、林龄、林分密度、林分结构等(Clarketal.， 2014)，总体上可以分为内部因子(主要指林分因子)和外部因子(主要指气候因子)两大类(Zhangetal.， 2017)。

气候因子是单木胸径生长变化的重要驱动因子，已引起学者广泛关注(Allenetal.， 2015； Hanewinkeletal.， 2012)。Henderson 等(2009)建立长叶松(Pinuspalustris)胸径生长与气候因子之间的关系模型，结果表明在所有气候变量中，温度是最弱的驱动因子。黎敬业等(2019)分析马尾松(Pinusmassoniana)径向生长与气候因子的关系，结果发现高海拔地区马尾松径向生长对气候因子年际波动敏感性较强，与生长季前冬季光温条件和生长季内7月降雨呈正相关，生长-气候关系在不同样点间表现出较强一致性。王延芳等(2020)基于 Vaganov-Shashkin 模型模拟青海云杉(Piceacrassifolia)径向生长，结果表明降雨对祁连山中部低海拔地区青海云杉径向生长具有决定性作用。

对于林分因子，包括林分密度(Zhangetal.， 2015)、立地(Aragaoetal.， 2009)、年龄(Fosteretal.， 2014)等对单木胸径生长变化的驱动性也不小。通常来说密度越大，单木胸径生长量越小，立地条件越好，单木胸径生长量越大(DeRoseetal.， 2009； Zhangetal.， 2015)。王冬至等(2017)分析华北落叶松(Larixprincipis-rupprechtii)-白桦(Betulaplatyphylla)针阔混交林胸径生长，结果表明年龄和竞争指数与胸径生长量呈负相关关系，胸径和林分优势高与胸径生长量呈正相关关系。张海平(2017)构建基于气象因子的天然白桦林单木胸径生长模型，结果发现温度和降雨有利于白桦生长。

综上可知，气候因子和林分因子对单木胸径生长均有一定驱动性。在进行模型分析选择变量时，一般大部分研究都是主观指定包含某些变量的某个特定模型为最优模型，由此导致所建立模型的预测能力减弱，这是频率统计模型的一个弱点。如逐步回归法(stepwise regression, SR)根据变量显著性(P)，选择显著的变量保留在模型中； 而实际上事先并不知道包含哪些变量的模型为最优模型，即模型本身存在不确定性(Rafteryetal.， 1991； Draper， 1995)。当基于研究数据建立回归模型时，若忽略模型本身的不确性仅以某一特定模型进行分析，一方面会低估模型的不确定性，高估预测结果，限制模型的适用范围； 另一方面会比正常情况下更趋向于拒绝无效假设，从而产生误导性结果(Viallefontetal.， 2001； 张志杰等， 2007)。

贝叶斯模型平均法(Bayesian model averaging，BMA)是近些年发展较快的一种多因子和模型不确定性分析方法(Picardetal.， 2012)。与传统分析方法不同，BMA并非仅指定一个最优模型，而是考虑模型空间内所有可能的模型以及各模型的后验概率，将模型的后验概率加权平均得到贝叶斯平均模型，并根据模型中变量估计值不等于 0 的后验概率进行变量重要性排序，判断各模型出现的可能性(罗剑锋， 2003)。近年来，BMA 在林业领域也有些研究，如Bullock等(2007)成功地将 BMA 应用于林木胸径分布中、Picard等(2012)利用 BMA分析了热带森林地面生物量、Zhang 等(2014)利用 BMA 构建了杉木(Cunninghamialanceolata)林分断面积生长模型、Lu等(2019)利用BMA构建了枯损率模型等； 但是，在错综复杂的影响因子中如何更好地选择因子，并构建不确定性胸径生长模型还未见报道。

杉木是我国速生高产用材树种之一，也是我国南方亚热带地区最重要的乡土栽培树种。据第九次全国森林资源清查结果，杉木人工林总造林面积达 990.2万hm2，占全国十大主要造林树种面积的27.23%，蓄积占32.57%，均居各大造林树种之首。本研究拟探索杉木人工林单木胸径生长量变化的驱动因子，比较不同驱动因子的重要性，构建不确定性单木胸径生长模型，以期为杉木经营管理者科学经营管理杉木人工林提供参考。

1 研究区概况与数据调查

研究区位于福建省邵武市卫闽林场(117°43′E，27°05′N)，为杉木中心产区，地貌主要为低山、高丘，海拔250～700 m，坡度25°～35°。属亚热带季风气候，年均气温17.7 ℃，1月平均气温6.8 ℃，7月平均气温28 ℃，极端低温-7.9 ℃，年均降雨量1 768 mm，年均相对湿度82%。

研究区杉木密度试验林为1982年使用1年生苗木造林，采用随机区组试验设计，设置5种密度： A，2 m×3 m(1 667 株·hm-2)； B， 2 m×1.5 m(3 333 株·hm-2)； C，2 m×1 m(5 000 株·hm-2)； D，1 m×1.5 m(6 667 株·hm-2)；E， 1 m×1 m(10 000 株·hm-2)。每种密度重复3次，共设立样地15块，每块样地大小为20 m×30 m。造林后1984—1990年逐年调查，之后到2010年隔年调查，每次调查均在秋冬季进行。测量树高时，每块样地随机抽取50株树，计算最高5株树的平均高作为林分优势木平均高。

2 研究方法

2.1 变量选择

内部因子主要指单木大小因子、竞争因子和林分因子。单木大小因子包括胸径(diameter at breast height, DBH，cm)、年龄(age,A,a)； 竞争因子包括胸高断面积(basal area, BA，m2·hm-2)、大于对象木的断面积和(sum of basal areas of trees larger than the subject tree, BAL，m2·hm-2)； 林分因子包括林分密度(number,N，trees·hm-2)、优势木平均高(dominant height,Hd，m)、林分平方平均胸径(quadratic mean diameter,Dg，cm)。内部因子统计值见表1。

外部因子主要指气候因子，通过ClimateAP软件获得(Wangetal.， 2012)，包括年均气温(mean annual temperature，MAT，℃)、年均降雨量(mean annual precipitation，AP，mm)、最冷月平均温度(mean coldest month temperature，MCMT，℃)、年均干旱指数(annual heat-moisture index，AHM)、低于0 ℃天数(degree-days below 0 ℃, DD0, d)、夏季平均最高温度(summer mean maximum temperature，SMMT，℃)、冬季平均最低温度(winter mean minimum temperature，WMMT，℃)、最热月平均温度(mean warmest month temperature，MWMT，℃)和春季平均气温(spring mean temperature，SMT，℃)。气候因子统计值见表2。

表2 气候因子统计值①Tab.2 Summary statistics of climate factors

2.2 模型构建

根据树木生长规律，胸径生长量(annual increment of DBH, AID)大于或等于0; 但是当AID等于0时，其对数变换lnAID无法计算。为避免这些误差，Calama等(2005)和李春明(2012)在对数变换之前给胸径生长增加常数1，以胸径生长量加1的对数值ln(AID +1)为模型因变量。本研究构建的胸径生长量模型形式如下：

ln(AID+1)=x0+x1lnDBH+x2DBH+

x3BA+x4Dg+x5Hd+x6lnA+x7N+

x8BAL+x9MCMT+x10AP+x11AHM+

x12SMMT+x13WMWT+x14SMT+x15MAT+

x16DD0+x17MWMT。

(1)

其中： AID为 1984—2010 年每2年间隔的年均胸径生长量(为排除不同间隔期带来的影响，仅研究每2年间隔的年均胸径生长量)；x0～x17为参数。

数据的对数变换会导致胸径生长量估计偏差，Baskerville(1972)给出了对这种偏差进行修正估计的近似值：

(2)

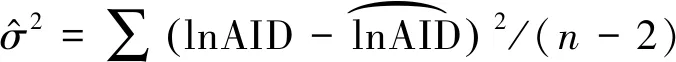
2.3 BMA原理

假设y为研究感兴趣的量(胸径生长量)，Z为调查所得数据(气候因子和内部因子)，f={f1,…,fk}(k=1,…,n)代表所有可能模型组成的模型空间，而包含哪些变量的模型为最优模型事先并不知道，即模型本身存在不确定性。通常情况下，可以考虑的模型数量很大，如有p个自变量，那么在仅考虑主效应时其模型数量为2p。BMA选取可能模型的子集，并用这些模型的后验概率进行所有推理和预测(Kassetal., 1995)。根据贝叶斯模型平均法，y的后验分布为：

(3)

式中：P(y|fk,Z)为给定调查数据Z和模型fk条件下y的后验分布；P(fk|Z)为给定调查数据Z条件下fk为最优模型的概率。

由方程(3)可知，y的后验分布实际上是以后验概率P(fk|Z)为权重对所有模型后验分布进行加权的一个平均值。在方程(3)中，假定fk为最优模型，则概率分布为：

(4)

式中：β=(β0,β1,…,βn)为模型fk回归系数的向量。

对于变量的先验分布，本研究利用无信息先验分布(Boxetal.， 1973)。

模型空间中所有模型数量很大，假设自变量为5个，那么即使不考虑变量间的交互作用，可构建的模型也可达32个，然而在实际研究中只有满足要求的模型才能被选进来。Madigan等(1994)建议采用Occam窗法排除不当的模型以减少模型数量： 当一个模型后验概率小于最优模型后验概率的5%时，则从模型空间中移除该模型。本研究采用Occam窗法排除不当的模型，排序得到后验概率大的模型。

根据贝叶斯理论，备择假设H1为：Xk为杉木单木胸径生长量变化驱动因子的后验概率有多大，即βk不等于0的后验概率有多大。BMA以所有包含变量Xk的杉木单木胸径生长模型后验概率的和作为βk不等于0的后验概率的估计：

(5)

式中：Ii为0/1指示变量，当βk在模型fi中，Ii=1，反之Ii=0；Ω为模型空间。

Kass等(1995)认为,BMA变量后验概率推断的规则如下：P(βk≠0|Z)<0.5，表示没有证据表明Xk是杉木单木胸径生长量变化的驱动因子； 0.5 ≤P(βk≠0|Z)<0.75，表示有弱的证据表明Xk是杉木单木胸径生长量变化的驱动因子； 0.75 ≤P(βk≠0|Z)<0.95，表示有强的证据表明Xk是杉木单木胸径生长量变化的驱动因子；P(βk≠0|Z)≥0.95，表示有很强的证据表明Xk是杉木单木胸径生长量变化的驱动因子。

若Xk是杉木单木胸径生长量变化的驱动因子，则根据BMA模型似然函数推导得出杉木单木胸径生长模型中变量因子Xk的点估计的后验概率均值为：

(6)

之后对该变量后验概率均值进行排序，选择杉木单木胸径生长量变化的主要驱动因子，并构建相应的不确定性胸径生长模型。

2.4 模型评价

采用决定系数(R2)和平均绝对差(mean absolute difference, MAD)作为模型预测的评价指标。R2越大、MAD越小，模型精度越高：

(7)

(8)

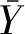
为探究不同初植密度单木胸径生长响应差异，本研究分不同密度以及所有样本进行分析处理。在不同处理中，随机抽取总数据的60%作为建模数据，剩余40%作为检验数据。同时，分别利用BMA和SR(双向选择)2种方法分析杉木单木胸径生长量与内部和外部因子的关系。BMA分析通过R软件BMA包实现(Rafteryetal.， 2005)，SR分析通过step函数实现。

3 结果与分析

3.1 BMA和SR确定的最佳模型比较

在E密度中，SR确定的模型与BMA确定的最优模型相似。在A和D密度中，SR确定的模型与BMA确定的第二优模型相似。在B、C密度和全样本数据中，SR确定的模型不在BMA确定的后验概率较大的前几个模型中(表3)。B、C密度和全样本数据3种处理在模型选择上表现出明显差异。

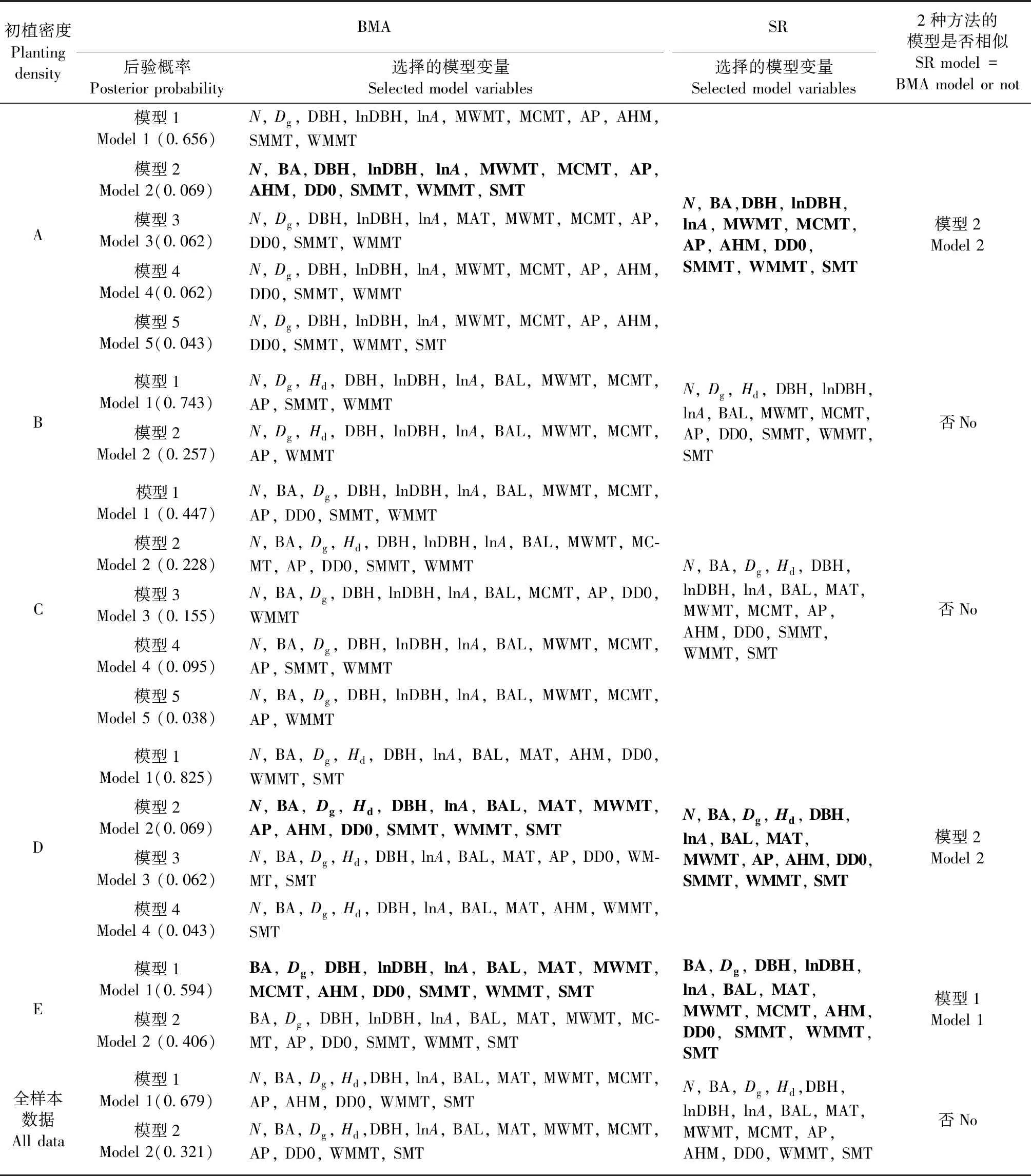
表3 BMA和SR确定的单木胸径生长模型和BMA模型的后验概率①Tab.3 Individual tree diameter growth model by BMA and SR methods and posterior probability of BMA model

除此之外，2种方法确定的模型R2和MAD在5种密度水平和所有密度水平的集合数据集中几乎相同，模型预测效果没有明显差异(表4)。

表4 基于BMA和SR的单木胸径生长模型评价Tab.4 Evaluation of individual tree diameter growth model based on BMA and SR methods

3.2 BMA和SR的参数估计值和P比较

A密度：BMA模型中，单木胸径生长量随DBH、MWMT、MCMT、AP和AHM增加而增加，随N、Dg、lnDBH、lnA、SMMT和WMMT增加而减小；SR模型中，单木胸径生长量随BA、DBH、MWMT、MCMT、AP、AHM、DD0和SMT增加而增加，随N、lnDBH、lnA、MAT和WMMT增加而减小(表5、图1)。

B密度：BMA模型中，单木胸径生长量与Hd、DBH、MWMT、MCMT和AP呈正相关关系，与N、Dg、lnDBH、lnA、BAL、SMMT和WMMT呈负相关关系；SR模型中，单木胸径生长量与DD0和SMT呈正相关关系(表5、图1)。

C密度：BMA模型中，单木胸径生长量与BA、DBH、lnDBH、MWMT、MCMT、AP和DD0呈正相关关系，与N、Dg、lnA、BAL、SMMT和WMMT呈负相关关系；SR模型中，单木胸径生长量与Hd、MAT呈负相关关系，与AHM和SMMT呈正相关关系(表5、图1)。

D密度：BMA模型中，单木胸径生长量与BA、Hd、DBH和MAT显著正相关，与N、Dg、lnA、BAL、AHM、DD0、WMMT和SMT显著负相关；SR模型中，单木胸径生长量与AP和SMMT显著负相关，与MWMT显著正相关(表5、图1)。

E密度：BMA模型中，单木胸径生长量与BA、Dg、DBH、MWMT、MCMT、DD0和SMT呈正相关关系，与lnDBH、lnA、BAL、MAT、SMMT和WMMT呈负相关关系；SR模型中，单木胸径生长量也与AHM呈负相关关系(表5、图1)。

全样本数据处理中，BMA选择的变量与D密度相似，较D密度多选择了MWMT、MCMT和AP，且显著正相关，少选择了AHM；逐步回归模型中，单木胸径生长量与lnDBH显著负相关，与AHM显著正相关(表5、图1)。

在多数处理中，BMA和SR的年均胸径生长量随DBH、BA、MWMT、MCMT、AP增加而增加，随N、lnA、BAL、WMMT增加而减小，且随期初胸径增大，年均胸径生长量逐渐变小(图2)。Dg在A、B、C、D密度和全样本数据中与胸径生长量表现为负相关关系，但是在E密度中表现为正相关关系。与DBH不同，lnDBH只在C密度中与胸径生长量表现为正效应关系，在A、B、E密度中表现为负效应关系，在另外2种处理中与胸径生长量的关系不显著。MAT在中低密度(A、B、C密度)中对胸径生长量的影响不大，在D密度中表现为正效应关系，在E密度和全样本数据中表现为负效应关系。对于AHM、SMMT和SMT，BMA只在较少处理中认为与胸径生长量显著相关，但是SR在大多数处理中都选择了这些变量(表5)。

BMA认为，Hd在B、D密度和全样本数据中与胸径生长量呈正相关关系，与SR略有不同，SR认为在C密度中胸径生长量随Hd增加而减小。在A、B、C密度和全样本数据中，BMA认为胸径生长量随AP增加而增加；而在D密度中，SR认为AP与胸径生长量呈负效应关系。

此外，SR选择的变量比BMA更多。2种方法选择的内部因子几乎相同，BMA只在A密度中多选择了Dg，SR在A密度中多选择了BA，在全样本数据中多选择了lnDBH，但是在每种处理中，SR都比BMA多选择了气候因子。由此可见，SR更容易选择冗余变量到模型中(表5)。

4 讨论

4.1 BMA与SR的比较

本研究基于BMA与SR构建单木胸径生长模型，SR根据自变量对因变量的意义选择变量，但是容易忽略模型本身的不确定性； BMA的优点已在几种不同类型模型中进行了评估，如线性回归、生存模型等(Raftery， 1996； Volinskyetal.， 1997； Murphyetal.， 2001)，均表明BMA可提高模型性能。本研究结果同样表明，BMA在变量选择上优于SR。

采用SR拟合的模型在3种处理下位于BMA选择的后验概率高的前几个模型中，仅在E密度中具有与BMA选择最佳模型相同的预测变量(表3)，这表明模型本身存在不确定性，SR忽略了这一点。

表5 SR和BMA构建单木胸径生长模型的参数估计值①Tab.5 The parameter estimates of individual tree diameter growth model by BMA and SR methods

图1 不同密度处理下BMA模型各自变量后验概率Fig.1 The posterior probability of variables in individual tree diameter growth model determined by BMA method

图2 年均胸径生长量与期初胸径的关系Fig.2 The relationship between annual increment of DBH (AID)and diameter at the beginning of growth period

单木胸径生长模型中，BMA认为，Hd在B、D密度和全样本数据中与单木胸径生长量呈正相关关系，而SR认为，在C密度中单木胸径生长量随Hd增加而减小。一般情况下，胸径生长量应随优势高增加而增加。BMA认为，在A、B、C密度和全样本数据中单木胸径生长量随年均降雨量增加而增加，而在D密度中，SR认为年均降雨量与胸径生长量呈负效应关系。有研究发现，降雨量增加可以促进树木生长(余黎等， 2014； 张海平， 2017)。可见，BMA的结论比SR具有更大的可解释性。

此外，SR选择的变量比BMA更多，即选择冗余变量较多。单木胸径生长模型中SR选择了更多的气候因子，余黎等(2014)、欧强新等(2019)发现，单木胸径年均生长量受气候因子影响较小，而竞争因子和单木大小因子是影响单木胸径年均生长量的主要因子，这与BMA的结果是一致的。Genell等(2010)利用模拟数据表明，BMA不选择冗余变量的概率高于SR，且选择真实预测因子的概率与SR相似。

需要说明的是，2种方法在模型预测性能上的差异较小。Zapata-Cuartas等(2012)研究表明，对于小样本，贝叶斯方法的性能优于经典方法。Wang等(2019)将分层贝叶斯方法与非线性混合效应模型进行比较，并估计地上生物量，结果发现2种方法在大样本时表现相似，而对于小样本贝叶斯方法要好得多。

4.2 单木胸径生长量的影响因子

内部因子中，年均胸径生长量随单木期初胸径增加而增加，随lnA增加而减小，这表明单木期初胸径越大，单木生长优势越大，且在幼龄时增长迅速，随着年龄增加增长速度变缓，即随着期初胸径增大，年均胸径生长量变小(图2)。一些研究表明，期初胸径达到一定大小后，即达到大径阶后，其增长逐渐缓慢(张海平， 2017)。但lnDBH只在C密度中对年均胸径生长量有正效应影响，在3种处理(A、B、E密度)中与年均胸径生长量呈负相关关系。

年均胸径生长量随林分密度、林分平方平均胸径和大于对象木的断面积和增加而减小，与以往研究结果相同(Brooksetal.， 1998； Huangetal.， 2010)。大于对象木的断面积之和越小，林分内单木平均拥挤程度越小； 林分密度和林分平方平均胸径越小，林分内单木对生长空间的平均占有和利用越大，故单木年均胸径生长量越大(余黎等， 2014)。这都表明竞争越小，胸径生长量越大。但是在中高密度(C、D、E密度)和全样本数据中，胸高断面积对年均胸径生长量有正效应影响。在B、E密度和全样本数据中，年均胸径生长量随优势木平均高增加而增加，在其他处理中优势木平均高对年均胸径生长量没有影响。一般来说，树木生长与优势木平均高呈正相关关系，王冬至等(2017)研究华北落叶松-白桦混交林发现，立地质量对胸径生长量也具有一定影响，并与胸径生长量呈正相关关系，但影响较小。

气候因子中，最热月平均温度、最冷月平均温度和年均降雨量均对年均胸径生长量有促进作用。有研究发现，年均降雨量对冷杉(Abiesnephrolepis)胸径生长量表现为正效应关系，但达到一定阈值后表现为负效应关系(余黎等， 2014)，即当水分成为限制因子时，降雨往往对生长表现出正效应，而当水分充足或过多时，逐渐表现出负效应。也有研究发现，生长季水分多少可直接或间接影响细胞的分裂速率(程瑞梅等， 2015)，而且还在一定程度上影响生长季中树木体内营养物质的积累(姜倩倩等， 2012)。张海平(2017)研究发现，生长季最低温对年均胸径生长量表现为正效应关系。李文馨等(2015)发现，年均积温和年均降雨对胸径生长量有促进作用，该结果与本研究结果相反。

另外，在低密度(A密度)时，干旱指数越大年均胸径生长量越大，在高密度(D密度)时，干旱指数越大年均生长量越小。余黎等(2014)发现，年均胸径生长量随年均气温与年均降雨量之比增大而下降，与本研究在D密度的结果是一致的，在A密度呈正相关的原因可能是低密度时降雨对每株树都是充足的，所以干旱指数对年均胸径生长量没有抑制作用。

5 结论

本研究采用逐步回归法和贝叶斯模型平均法构建杉木人工林单木胸径生长模型，逐步回归法获得模型的后验概率小于BMA获得最佳模型(最高后验概率)或逐步回归模型不在BMA模型空间前几个后验概率高的模型中，由此表现出杉木单木胸径生长模型本身的不确定性。此外，逐步回归法更容易选择冗余变量。

内部因子和气候因子均会影响杉木单木胸径生长，但单木胸径年均生长量受气候因子的影响较小，而竞争因子和单木大小因子是影响单木胸径年均生长量的主要因子。单木胸径生长量随林分密度、林分平方平均胸径、大于对象木的断面积和、年龄、冬季平均最低温度增加而减小，随期初胸径、胸高断面积、优势木平均高、最冷月平均温度、最热月平均温度、年均降雨量增加而增加。总的来说，杉木单木胸径生长量随竞争增加而减小，随温度和降雨增加而增加。