电子元器件加速退化寿命评估方法研究
吕 瑛,王振宇,赵 岩,张会平,陈 娟
(1.北京遥感设备研究所,北京 100854; 2.北京控制与电子技术研究所,北京 100038;3.国营长虹机械厂,广西 桂林 541002; 4.北京航空航天大学 机械工程及自动化学院,北京 100191)
0 引言
本文以KBKu0583型大功率开关为例对电子元器件的加速贮存试验[1-3]结果进行了研究,并给出了寿命评估方法。前期采用步降应力法对大功率开关开展了加速贮存试验,依据产品规范和贮存故障模式及影响分析,确定了将插损指标作为主要的监测参数。试验中对插损性能指标进行了监测,对监测数据进行分析表明,大功率开关插损随着加速贮存试验时间变长,逐渐变大,有递增的变化趋势,因此将插损作为表征产品贮存期的指标。
通过上述加速贮存试验得到的是产品测试数据,还需要进行数据处理及评估得出加速因子、激活能以及产品的可靠性寿命。本项目采用退化轨迹法对产品的测试数据进行回归分析,得出多个伪寿命,进而估计出寿命分布参数,从而得出最终的加速因子、激活能以及产品的可靠性寿命等评估结果,达到了预期效果。
1 加速贮存试验简介
加速贮存试验是在不改变失效机理的条件下加大应力进行的贮存试验。它选择比正常使用环境恶劣的应力量级来加速产品失效缩短试验时间,在获得的失效数据基础上运用加速寿命试验模型对产品在正常应力量级下的各种寿命特征进行统计推断。加速退化试验是在不改变失效机理的条件下施加超过使用环境的应力加速产品的性能退化,得到高应力量级下的产品性能退化趋势,在此基础上运用加速退化模型对产品在正常应力量级下的各种寿命特征进行统计推断。
在进行加速寿命试验或加速退化试验之前,应先根据产品技术特性、已有贮存信息等摸清产品的应力极限,如果没有相关经验或历史数据参考,一般要求先进行加速贮存预实验以确定其贮存试验最高应力条件。预实验包括应力短时极限确认试验和应力耐久极限确认试验,分别用于确定产品应力短时极限和应力耐久极限。
KBKu0583大功率开关是一种利用具有矩磁特性的矩磁铁氧体材料结合激励电路制作的电控微波铁氧体器件,具有开关速度快、寿命长、可靠性高的优点。它用于发射机两个通道之间,实现两种状态切换。其内部主要由供电电路、控制电路、铁氧体材料组成。
由于整机的使用指标要求,本文对大功率开关的贮存可靠性[4-8]进行研究。贮存可靠性是指产品在规定的贮存条件下,规定的时间内,完成规定功能的能力。衡量产品的贮存可靠性指标主要包括贮存可靠度和可靠贮存寿命[9-11]。前期采用步降应力法[12-15]对KBKu0583型大功率开关开展了加速贮存试验,共获取了21组测试数据,其中插损有较为明显的变化趋势,绘制折线图如图1所示,均值与方差的变化如图2所示。

图1 大功率开关插损折线图
根据折线图分析,大功率开关插损随着加速贮存试验时间变长,逐渐变大,有递增的变化趋势。检测数据的均值与方差的变化如图2所示,插损趋势明显,能够表征产品的贮存期。按照本文描述的加速退化试验数据处理方法对其进行贮存寿命评估。

图2 大功率开关插损均值与方差变化折线图
2 数据预处理
通常采集到的加速试验数据,由于存在试验设备的控制精度、检测设备的系统误差及其工作环境差异等因素,使得数据看起来除了存在某种特定的退化趋势外,还存在一些异常值、与产品自身退化无关的趋势性波动等。如果试验对象是电子产品,试验应力是温度的话,由于温度的变化影响,还会存在产品温度漂移特性对加速试验数据的影响,数据会变得较为粗糙。为此,在对产品进行寿命和可靠性评估前,需要对试验数据进行预处理,主要是剔除异常值。
若共有N个加速退化数据,分别为yi(i=0,1,2,…,N-1),则yi为正常值的条件是:
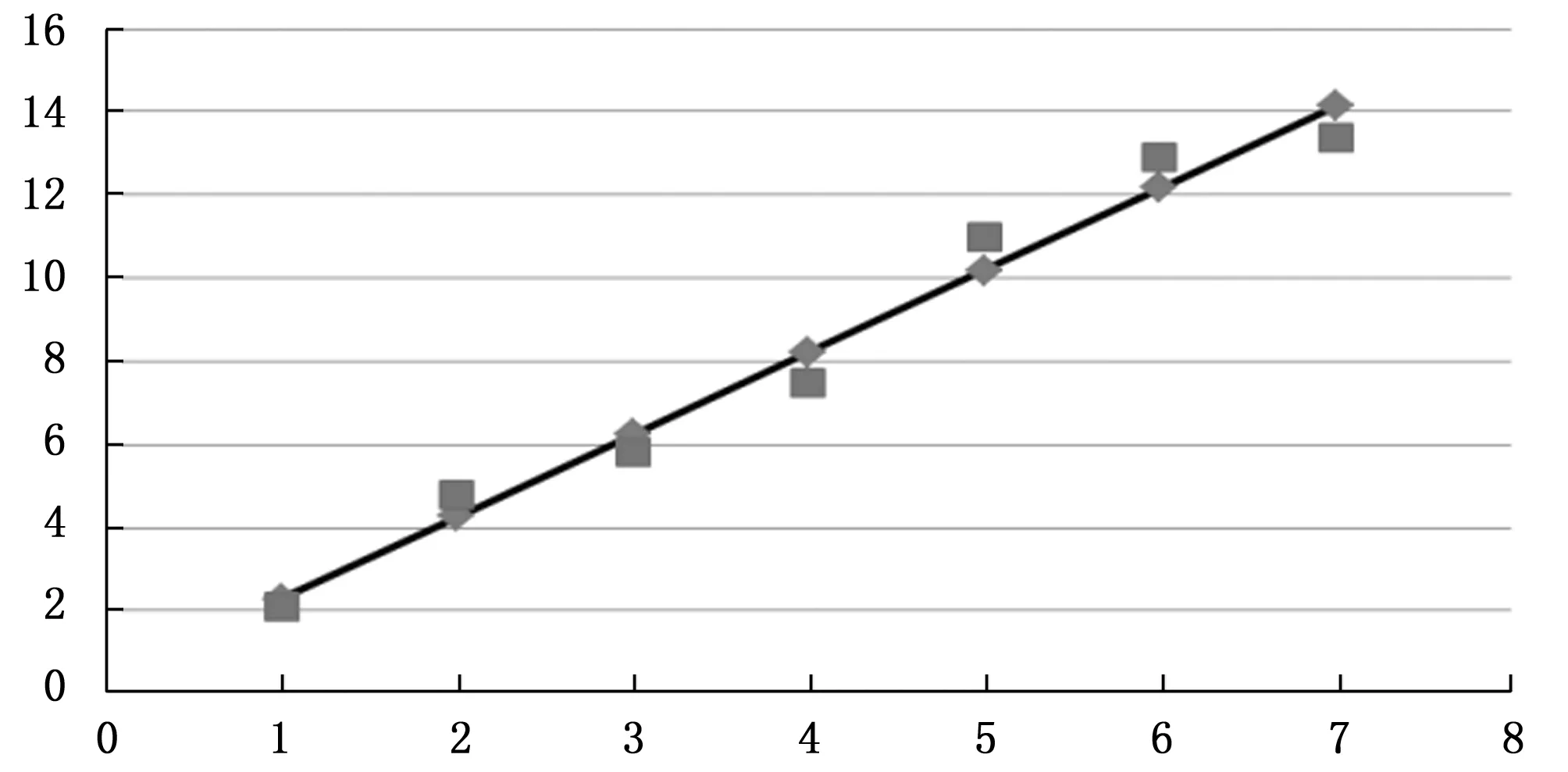
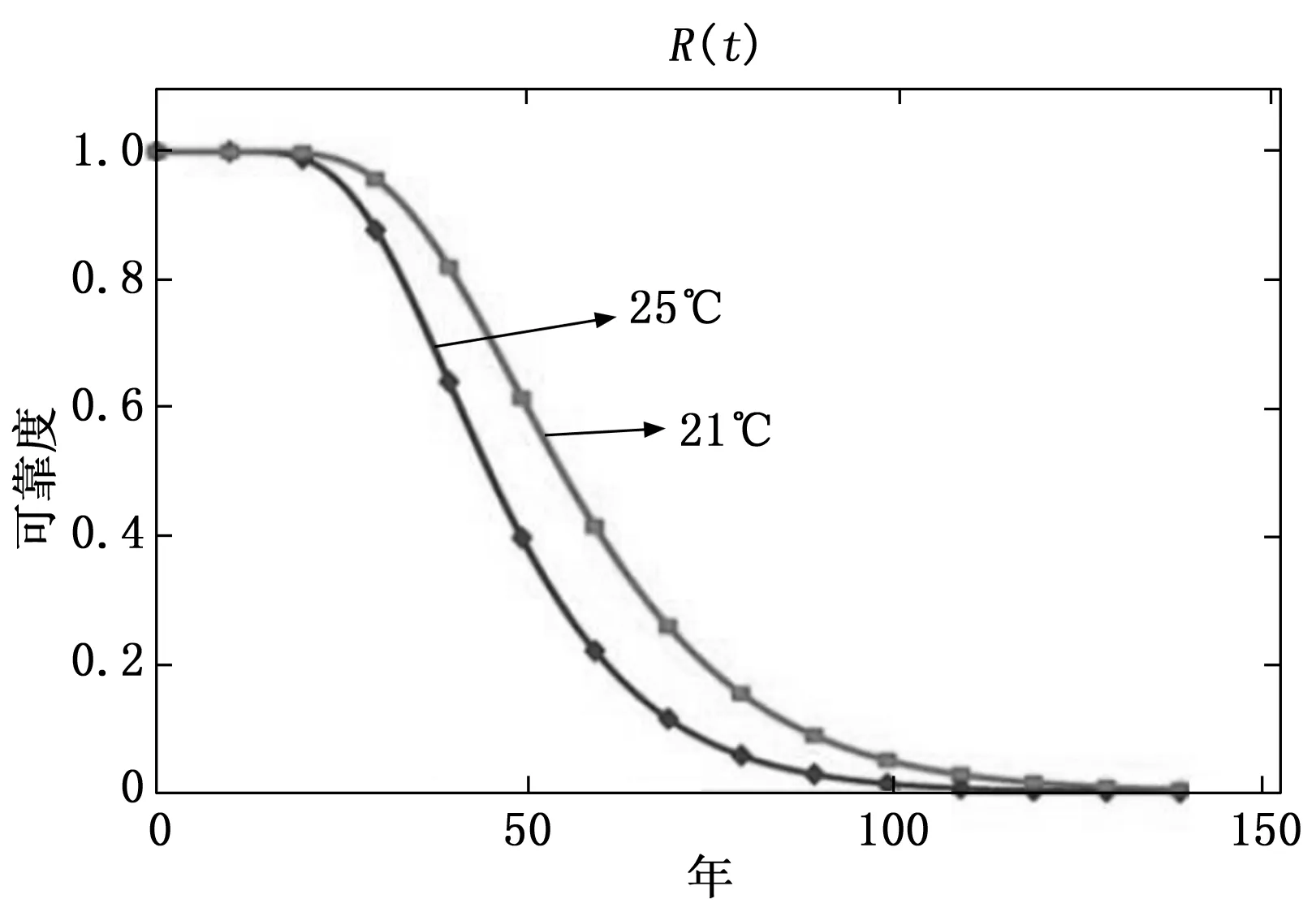
yi-1-KS (1) 其中:K为常数,通常取3~5。当不满足上述不等式时,yi判为不合理点,应从数据中剔除出去,该点性能值用如下外推值来代替: (2) 再使用移动平均滤波器对数据进行平滑处理,若原始数据为y,滤波后的数据为yy,移动平均滤波器的窗宽设置为5,yy中各元素的计算公式如下: yy(1)=y(1) yy(2)=(y(1)+y(2)+y(3))/3 yy(3)=(y(1)+y(2)+y(3)+y(4)+y(5))/5 yy(4)=(y(2)+y(3)+y(4)+y(5)+y(6))/5 yy(5)=(y(3)+y(4)+y(5)+y(6)+y(7))/5 (3) 当试验应力水平保持不变时,一般认为退化速率d(s)是常数。此时,可以采用回归的方法来估计该模型中的参数,为此建立下述线性回归方程: E(Y(t))=d(s)·t+y0 (4) 由于d(s)是描述应力与寿命关系的加速模型,它刻画了退化过程退化速率,因此当应力s越严酷时,性能退化速率就越快。以阿伦尼斯模型为例,此时应力s为温度T,即d(T)=Aexp(-B/T)。式(3)可写作: E(Y(t))=Aexp(-B/T)·t+y0 (5) 其中:T是绝对温度,单位K;B=Ea/k;k是波尔兹曼常数8.617 1×105eV/K;Ea是激活能,单位eV;A是常数。 如果将Aexp(B/T)作为一个未知整体,设slp=exp(AB/T),那么上式就是一个一元线性回归方程: E(Y(t))=slp·t+y0 (6) 当进行温度步进应力的加速退化试验时,温度在整个试验中呈阶梯式变化,因此对步降应力加速贮存试验的试验数据进行拟合时,需要分不同应力水平阶段评估不同的slp及加速模型参数A和B。下面将介绍如何针对这种情况进行一元线性回归方程式的参数评估。 Ei(Y(t))=slpi·t+y0i=1,…k (7) 以3水平的温度步进ADT为例,此时观测到的产品性能退化过程示意图如图3所示。 图3 步进加速试验性能退化示意图 图3以T3、T2、T1三个依次降低的温度标识应力水平的变化,可以看出,应力水平的阶梯式变化导致每个应力水平的性能退化速率不一样,从而导致试验中观测到的试验数据属于变环境数据。由于试验起始时刻不一样,T3温度应力开始之前产品有一组初始的参数测试值,可以作为T3温度下的初始值,通过线性方程推导失效的伪寿命。在T2温度下进行试验,试验的初始参数值是T3温度的结束测试值,不能通过简单向后外推获得伪寿命。为此,需要考虑在之前温度应力下消耗的寿命。 加速贮存试验中有两个重要的值,假设产品参数用Di来表示,D0代表产品的起始参数,Df代表产品的失效阈值,则在同一个步降应力加速贮存试验中,可认为D0和Df对所有温度应力值的试验过程都是恒定值。因此有下列等式成立: Df-D0=slpi·tn (8) 其中:Df为产品失效阈值;D0为产品试验前测试值;slpi为第i个应力水平下拟合退化直线的斜率;tn为第n个试验件的寿命。 根据上述公式,可以对每一组应力与退化速率数据进行最小二乘拟合,从而得到退化速率与应力水平的函数关系,具备了外推伪寿命的基础。 直线在数学中由于简单明了受到特别的关注。符合线性分布的试验数据可以描出一条直线,同样某些曲线经过一定的数学变换(如取对数、换元等)也可以用直线来表述,因此拟合出相对准确的直线具有特殊的重要意义。一般在描直线时,需要使直线与散点之间的偏差要尽量小,但毕竟因人而异。通过数据点的直线很多,利用最小二乘原则对散点进行直线拟合就是一个偏差最小的方法。其基本思想就是对应一个观测值的xi,用回归方程可计算一个yi,使回归直线y=kx+b的计算y值与观测值yi之差的平方和最小。 由于最小二乘法讲解的书较多,在此仅给出结果。对于拟合形如y=kx+b的直线,参数计算如下[16]: (9) 表示两个变量线性相关密切程度的数量指标成为相关系数,相关系数取值在0~±1之间,越接近±1说明变量的线性关系越密切,若用r表示,则: (10) 根据测试数据和上述公式,可以计算上述直线的参数,如图4。 图4 拟合直线示意图 通过回归分析,可以得出每个样本测试数据拟合的直线参数,由此可以外推得到产品在正常工作条件下的性能退化模型。通过该性能退化模型,很容易得出该性能从初始值D0到达失效阈值Df的时间。该时间就是产品该性能值在某特定应力条件下的失效时间,即贮存寿命。依次得出各个样本的外推失效数据,从而采用传统的方法,通过分布假设检验和参数估计,得到产品的寿命分布,从而得出可靠寿命评估结果。 基于上述评估思想,结合微波元器件和机电元器件本身的特点,采用对数正态分布进行寿命评估,对数正态分布[17-18]失效分布函数为: (11) 可靠度函数为: (12) 其中:μ为对数均值,σ2为对数方差,其密度典型曲线如图5所示。 图5 对数正态分布密度曲线 所有样本的失效数据都能外推得到,可采用最小二乘法对数正态分布的μ和σ进行参数估计: 由于Φ(Z)是标准正态分布,且: (13) 令x=lnt,则x=σZ+μ具有y=kx+b的线性形式,对于Z和x的一组数据,可以用最小二乘法求得回归系数k、b和相关系数r,并得到对数正态分布参数的估计值: (14) 电子元器件寿命还可能服从威布尔分布[17-18],需要分别用对数正态和威布尔两种分布进行拟合,同时计算出拟合优度,选择最合适的寿命分布开展贮存期评估。因此,有必要对威布尔分布的拟合方法进行研究。 威布尔分布失效分布函数[19]为: (15) 可靠度函数为: (16) 其中:m为形状参数,η为尺度参数,其密度典型曲线如图6所示。 图6 威布尔分布密度曲线 根据上文中描述的外推的方法,得到产品的伪寿命(包含寿命),可采用最小二乘法对威布尔分布的m和η进行参数估计: 对威布尔分布函数进行变形,取对数可以得到: (17) (17) 元器件从出厂经过贮存、运输、使用到失效的全寿命周期,无时无刻不在进行着缓慢的化学物理变化,实践证明,当温度升高以后,元器件退化的物理化学反应加快,失效过程加速。阿伦尼斯模型总结了由温度应力决定的化学反应速率依赖关系的规律,为加速寿命试验提供了理论依据。 本项目以温度作为加速应力,故采用阿伦尼斯模型[20],其一般方程式如下: (18) 加速因子公式如下: (19) 当元器件在t0时刻处于正常状态数M0,t1时刻处于失效状态数M1,如果温度与时间无关,则积分上式得: (20) 式中,t为元器件寿命;T为热力学温度;若令y=lnt,x=1/T,上述公式同样具有y=kx+b的线性形式,同理可用最小二乘法求解。 当获取上述公式中的参数估计值后,可以求出加速因子和激活能。利用试验温度下可靠度为0.5、0.9的寿命评估值,求出常温下两个可靠寿命,估计出常温下的可靠度寿命曲线,从而获得任意可靠度下的寿命。 假设不同试验温度下大功率开关插损寿命符合对数正态分布或威布尔分布,分别求出两种分布下的参数,然后通过假设检验给出最符合的寿命分布。将观测到的数据进行分组,选用统计量χ2作为反映统计分布与理论分布差异程度的统计量[20],用下式表示: (21) 式中,m为数据所分的组数;mi为落入第i组的频数;n为样本容量;Xi为按假设的理论分布计算得到的落入第i组的概率;nXi为第i组的理论频数。 根据检验作出是否符合此种分布的初步判断,若同时满足两种分布,依据公式(10)计算相关系数,相关系数大的分布更符合实际情况。 按照有退化趋势的数据分析方法对KBKu0583大功率开关插损测试数据进行处理。首先对数据进行剔除野值等常规处理,然后对全部样本测试值用最小二乘法进行线性拟合得出退化方程。根据退化方程,结合样品的初始值和失效阈值进行伪寿命预测,得出在不同温度下插损参数表征的伪寿命,概率密度曲线如图7所示。 图7 伪寿命分布的概率密度 假设不同试验温度下大功率开关插损寿命符合对数正态分布或威布尔分布,为验证统计得到的伪寿命分布函数的符合性,用最小二乘法分别估计出各温度点下不同分布的相关系数见表1所示。 表1 伪寿命拟合分布的相关系数r 由表1可以看出,用对数正态分布拟合的相关系数大于威布尔分布拟合的相关系数,表明大功率开关的伪寿命更符合对数正态分布。 利用不同试验温度下的寿命数据,根据阿伦尼斯方程计算插损参数表征的贮存寿命,考虑到本批次产品为2016年生产,应该在这个贮存期上再增加3年,给出KBKu0583大功率开关贮存期如表2所示。 表2 KBKu0583大功率开关贮存期(年) 给出分布函数并计算贮存26年的可靠度如下: (22) 表3 大功率开关可靠度参数 作出大功率开关贮存可靠度曲线如图8所示。 图8 KBKu0583大功率开关贮存可靠度曲线 本文论述了基于退化轨迹的产品寿命评估方法,对退化模型的选取,退化轨迹拟合和参数评估进行了研究,并以大功率开关为例开展了贮存寿命评估,给出了符合预期的评估结果,验证了上述寿命评估方法的可行性和有效性。3 参数退化模型
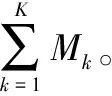

4 最小二乘法估计

5 基于退化数据的对数正态分布及威布尔分布参数估计


6 基于退化数据的威布尔分布及其贮存可靠度估计


7 加速因子模型及常温贮存寿命评估

8 寿命分布的假设检验
9 贮存寿命评估



10 结束语

