浅谈电动力学中的对称思想
肖慧宁
(石河子大学理学院物理系应用物理学专业 新疆 石河子 832003)
在《庄子 天下》中有这样一句话,“判天地之美,析万物之理”。意思是能够体会天地万物的美丽,能够了知天地万物的生存道理。在物理这门自然科学中,就包含了许多美学思想,而在电动力学这门课中,体现最多的莫过于对称美了。
1.对称思想
什么是对称?对称是指对某个物体施加某种操作,操作前后的情况相同。对称美在自然界中有很多体现,对称的思想也早已渗透到人们的心中。对称分很多种:左右对称,中心对称,平移对称等等。自然界的很多物体都是对称的,正如一片雪花,一朵向日葵都是中心对称的,而生物体的身体外形都是左右对称的;我们在生活中也总追求一种对称的和谐美,例如,我们的建筑总是追求左右对称,故宫、天坛这些名胜古迹就是很好的例子。在我们学习生活中,也经常会接触到对称。在自然科学里,对称原理是自然科学理论构建的基本法则:数学中的等式,物理中的方程,化学里的反应式等,这些学科中都包罗着对称的美学思想;同样,人文科学也离不开对称,我们以一些诗词古文为例:“物华天宝,人杰地灵”,“海阔凭鱼跃,天高任鸟飞”,“非淡泊无以明志,非宁静无以致远”。这些诗句读起来朗朗上口,很有气势,正是因为它们的创作是讲究对称的。
在物理的各个分支中,也存在许多对称:在力学中,自由落体和竖直上抛在同一位置对应的物理量对称;在光学中,光的反射、折射、干涉、衍射都具有实物对称美;在电磁学中,电场线和等势面的分布也具有对称美。同时,物理规律也具有对称性:在北京的物理定律和南京的物理定律是一样的,这体现了物理定律的空间平移对称性;两千年前古时的物理规律和两千年后的现在是一样的,这体现了物理规律的时间平移对称性……
2.电动力学中的对称
2.1 电与磁的对称。在电动力学中,最基本的两个实验定律为库仑定律和毕奥-萨伐尔定律,由此可得静电场的电场强度分布的积分形式和恒定电流激发的磁场分布规律的积分形式:

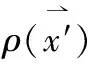
我们再来看电动力学的基础,最美物理方程之一——麦克斯韦方程组:

它将高斯定理、法拉第电磁感应定律、安培环路定理统一起来,完美地呈现了电场和磁场相互转化所产生的对称性,并统一了电磁场。就像一面镜子的两边,一边是“电”、一边是“磁”,变化的电场可以激发磁场,变化的磁场又能反过来激发电场,二者相互激发,互为因果,相辅相成。在麦克斯韦提出这组方程后,电和磁理论从此走向统一,两者由分离存在而合成了一个“电磁场”。
在电磁理论中,很多引入的物理量都表现出电与磁的对称性。例如,点电荷和电流元,电场线和磁感线,电场强度和磁感应强度,介电常数与磁导率等等。为了便于记忆,让知识体系更加系统,现整理一些电磁场中对应的物理量如下:

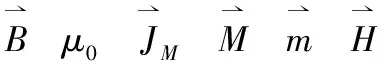
这样,在记住电场中的公式后,磁场中的公式就很容易类比地写出来。我不由感叹,物理学家在引入符号和公式时,尽可能朝简单、对称和谐的方向努力,使得我们现在看到的电磁场理论如此系统完美。
DeviceManager.GetInstance().DeviceAtIndex(EnumDevice.AI16AO2).ReadData(ref data,1); //设备调用,获得经过滤波处理的数据
2.2 解题中由对称思想引入的简化。
2.2.1 分离变量法中轴对称引入的简化。在许多实际问题中,静电场的性质取决于带电导体的电荷分布,这些问题的本质归结于自由电荷只出现在导体的表面,而在空间的其他位置没有其他电荷的分布。此时,可以将导体表面作为该区域的边界,则在该区域内部,自由电荷密度ρ,则泊松方程可化为较简单的拉普拉斯方程:▽2φ=0,其通解可由分离变量法求出:
(在球坐标中)
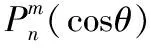
这时的通解看起来比较复杂,但若在具体问题中具有对称轴,通解的形式就会大大得到简化,下面举例说明。
例1:一个内径和外径分别为R2和R3的导体球壳,带电荷Q,同心地包围着一个半径为R1的导体球(R1 图1 具有球对称性的导体球 将φ1,φ2代入边界条件,可解出a,b,c,d由此得出: 例2:电容率为ε的介质球置于均匀外场E0中,求电势。 图2 具有轴对称性的介质球 如图2,研究对象为置于均匀外场中的介质球,此时具有轴对称性。以φ1代表球外区域电势,φ2代表球内区域电势,则可设 其中,anm,bnm,cnm和为待定常数。再根据题目列出边界条件,代入即可求解。 由以上两例可见,对于可用分离变量法解决的问题,首先应该画出题目的模型简化图,找出模型的对称轴,充分利用其对称性,可使通解形式变得更加简洁,大大简化计算过程。 2.2.2 由对称思想产生的“镜像法”。当区域内只有一个或几个点电荷,区域边界是导体或介质界面时,利用对称思想可以很大地简化问题,简单快速进行解答。假设点电荷周围有一个导体,在点电荷的作用下,导体上出现感应电荷。“镜像法”利用电场中的对称性,用导体内部的一个或多个假想电荷来替代导体面上的感应电荷对空间的电场产生的影响。此时,空间中的电荷分布没有改变,因此泊松方程也不变,只要确保这种代换使边界条件得到满足,问题就可以简单地解决。下面举例说明。 例3:接地无限大平面导体板附近有一点电荷Q,求空间中的电场。 无限大接地平面导体板附近有一个点电荷Q,在Q的作用下,导体板上会出现感应电荷。此时空间中的电场是由点电荷Q和感应电荷共同激发的,导体表面为零势能面,电场线与导体表面处处垂直。 图3 引入“镜像电荷”后的空间电场分布 如图3,我们设想导体板为一面“镜子”,在下面关于“镜子”对称的地方有一个假想电荷(“镜像电荷”)-Q,此时抽取导体板,电场线与原导体板平面仍处处正交,边界条件得到满足。此时,导体板上部空间的电场可看作由原电荷Q和“镜像电荷”-Q共同激发的,将Q在导体板上的投影点作为坐标原点,设Q到导体板的距离为a,则空间一点的电势为 通过上面的例子,我们可以看出,充分地利用问题中的对称性,巧妙地将感应电荷用“镜像电荷”代替,可以化未知问题为已知问题,快速找到问题的解。 物理学家费曼认为,科学的第一步是猜想,这是一个靠自己的美学直觉去发现的过程。自然中真的东西必然表现出令人震撼的美,美是发现真理的向导,科学家们朝着美的方向,努力探索自然规律,深入分析事物的内在矛盾,发挥想象力和创造力,构筑质朴统一和谐理论体系。 除了对称美,物理学的美还体现在其他方面:物理公式和定理总是追求统一美,比如牛顿力学中的万有引力是“平方反比”的形式,而电磁场中的库仑定律也是“平方反比”的形式;爱因斯坦晚年一直致力于的“统一场论”,也是为了将四种相互作用统一起来。物理模型和理论总是追求简单美,在哥白尼发现日心说前,人们一直认为地球是宇宙的中心,太阳,月亮,行星和恒星都绕着它运动,为了说明这些行星的运动轨迹,物理学家们认为它们沿附在相应天球上的更小的圆周运动。尽管这种模型十分复杂,但是由于这满足了当时的基督教会奉行的理论,于是被普适接受。后来,当实际观测水平的提高和观测数据的增加,哥白尼提出了一个更简单的模型——太阳位于中心,地球和行星绕太阳运动,这个理论的提出,使天体的运动变得简单了许多,于是逐渐被大众所接受。在简单和复杂之间,物理学家一定会选择最简洁的形式,来揭示这个世界的真相。 尽管很多物理理论都会表现出对称性和完美性,我们也不能否定一些导致不完美的“破缺”。完美的东西固然是美的,但是不完美往往能引出一系列前所未有的发现。追求完美固然不错,但是物理学家在发现了不完美后,不是去遗憾这种“不完美”,而是去努力发现这种“不完美”背后的原因,从而获得一些新的发现。同时,正是因为不完美的存在,才使得这个世界变得如此多姿多彩。 我们在学物理时,并在掌握基本公式定理的同时,要对所有学内容进行对比,触类旁通,举一反三,将不同的课程联系起来,发掘它们之间的联系与差异。还应深入思考,理解它们内在的思想,探寻物理学家们引入物理定义和物理符号时的用心,这样既可以更深地领悟物理定律背后的美学思想,又能反过来更好地理解我们的物理理论。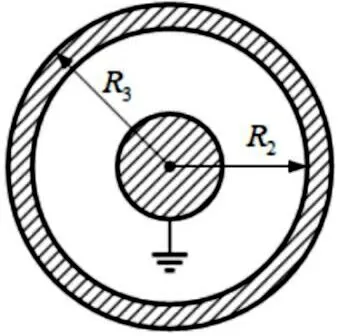
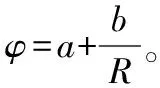
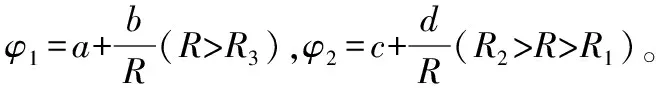
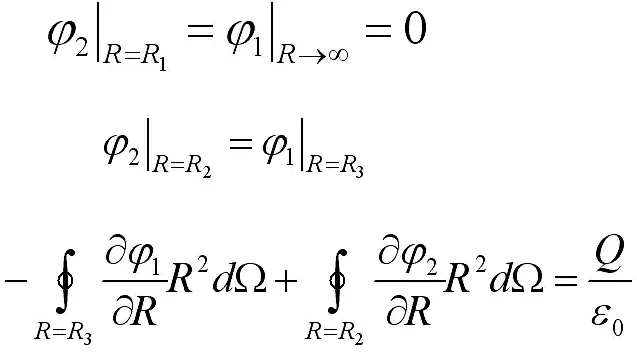
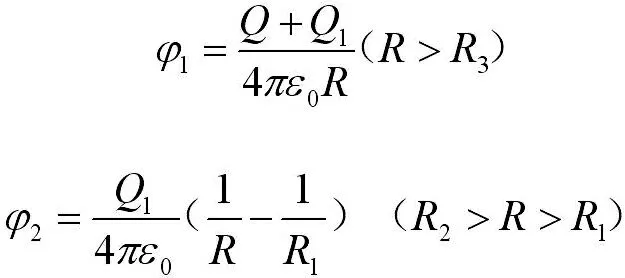




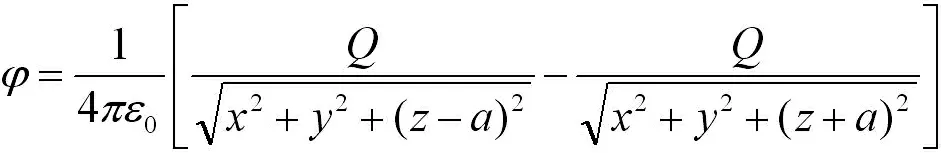
3.美学是发现真理的向导

