基于置信规则库的交通监控调度方法研究
李康乐,孙 超,朱海龙
(1 哈尔滨金融学院 计算机系,哈尔滨 150030;2 哈尔滨师范大学 计算机科学与信息工程学院,哈尔滨 150025)
0 引言
对于交通路口来说,全天候的监控是非常重要的,在违法行为的监督调查,公共安全和交通调度等方面发挥着重要作用。在多摄像机监控系统中,由于摄像机的数量和实时调度带来的复杂性增加,使用手动协调和控制摄像机监控目标变得十分困难。
目前,许多学者采用了多种方法从多个角度研究监控调度问题。Chen 等人[1]使用神经网络对摄像机调度进行研究。Spaan 等人[2]提出了一种基于自定义目标的带有信息奖励的部分可观察马尔可夫链模型(Partially Observable Markov Decision Process with Information Rewards,POMDP-IR)框架来选择最优的静态监控摄像机。马庆平[3]将目标优先级这一条件加入到基于POMDP 的多监控摄像调度算法中,将主动监控与被动监控进行结合得到摄像机-目标组合。Song 等人[4]用博弈论的方法解决不同焦距下的监控问题。王洪亮[5]提出了一种分布式多摄像机协同监测方法。
近年来,对监控调度方法的研究主要分为3 类:以数据驱动为核心的机器学习方法、以定性知识为核心的专家系统、以及基于马尔可夫过程的决策理论。其中,基于数据的机器学习方法在摄像机调度领域存在对数据和模型要求高、对多个复杂路网通用性差、过程可解释性困难等问题。在基于知识的专家系统中,模拟人的知识和思维是建立在监控过程中的知识和规则基础上的,对专家知识的要求较高,模型准确性低。在基于马尔可夫过程的决策理论中,对静态摄像机和云台摄像机有很高的要求,需要通过物理空间进行定位和判断。为了解决摄像机调度过程中的上述问题,本文提出了一种基于BRB的交通监控摄像机调度方法。
BRB 是一个由多个置信规则组成的专家系统,由Yang 等人于2006 年提出,该方法能够将信息的不确定性加入到模型当中并有效地对其进行表示及处理,从而建立一个可清晰表示输入与输出之间非线性关系的模型[6]。在规则库创建完成后,使用ER 对置信规则进行融合推理[7-8],最后使用效用理论得出最后融合结果[9]。与传统方法不同,对信息的模糊不确定性以及概率不确定性具有较好的表示能力,因此对于具有非线性特征的数据,具有较好的建模效果[10],并且其建模过程具有可解释性[11]。基于BRB 的复杂系统建模方法在生产规划、医疗决策和安全评估中有着广泛的应用[12-14]。
1 问题描述
在交通摄像机调度中,调度过程可以分为以下步骤:
第一步:监控数据获取。
第二步:数据传输。
第三步:数据处理。
第四步:拍摄质量判断。每台相机的拍摄质量根据实际情况而定。
第五步:摄像机调度。根据设定的模型,通过捕捉数据对摄像机进行调度。
在监控摄像机调度过程中,调度问题可以描述为:

其中,y表示调度结果;X表示输入数据;α表示参数集;f(·)表示模型求解过程。
首先将输入设置为拍摄效果,即拍摄时的拍摄质量。由于距离、角度等的影响,同一类型相机捕捉到的同一目标是不同的,因此使用距离和角度等参数作为输入来评价相机的质量。
2 构建监控调度模型
2.1 模型构建
BRB 中含有许多置信规则,其中第k条规则可描述如下:
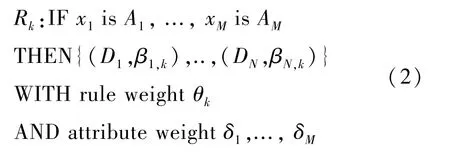
其中,Rk表示BRB 中的第k条规则;x1,x2,...,xM为第k条规则中的M个前提属性;A1,A2,...,AM为第k条规则中M个前提属性对应的参考值;D1,D2,...,DN为第k条规则的N个结果;β1,β2,...,βN为第k条规则中N个结果对应的置信度;θk为第k条规则的规则权重;δ1,δ2,...,δM为第k条规则中M个前提属性的属性权重。
2.2 模型推理
2.2.1 计算规则匹配度
在规则库创建完成后,首先需要对输入信息进行转换来计算所有规则的规则匹配度,具体的计算方式如式(3)所示:
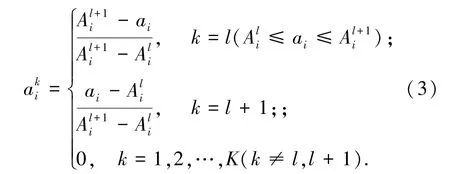
其中,ai表示第i个属性的输入数据;表示在第k条规则中输入数据对第i个属性的匹配度;表示第l条规则中第i个前提属性的参考值;K表示BRB 中规则总数。
2.2.2 计算激活规则的激活权重
在置信规则库中包含有许多规则,有些规则在输入信息转换完成后是没有被激活或者激活程度比较小的。通过计算规则的激活权重,可以得到输入数据对每条规则的激活程度,具体计算方式如式(4)所示:
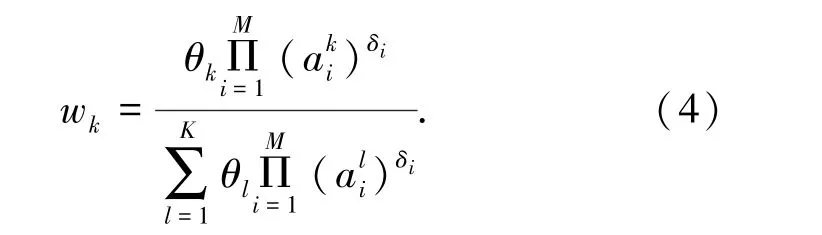
其中,wk表示第k条规则的规则激活权重;θk表示第k条规则的规则权重;M表示前提属性的数量;K表示BRB 规则库中的规则总数。
2.2.3 规则组合
在规则库中的规则被激活以后,接下来就需要对所有激活的规则进行规则组合,得到综合的评价结果。融合方式采用ER 进行融合,融合方法如式(5)和式(6)所示:
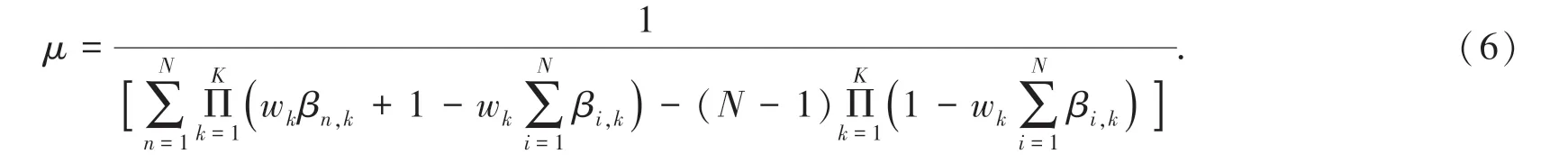
其中,βn表示对第n个结果的置信度,是综合规则库中所有规则所推理出的结果。
2.2.4 计算效用值
规则组合完成以后,根据效用理论,计算最终输出的效用值,就可以得出模型的最终输出结果,计算方式如式(7)所示:
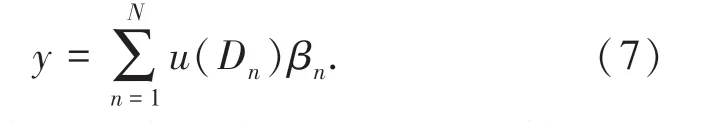
其中,y为模型的输出结果,u(Dn)为结果Dn的效用值。
2.3 模型优化
BRB 模型的初始参数由专家给出,其中含有一定的不确定性以及模糊性。因此,为了得到更好的建模效果,需要对BRB 的初始参数进行优化。
基于P-CMA-ES 的模型参数优化方法[15]可以描述为:
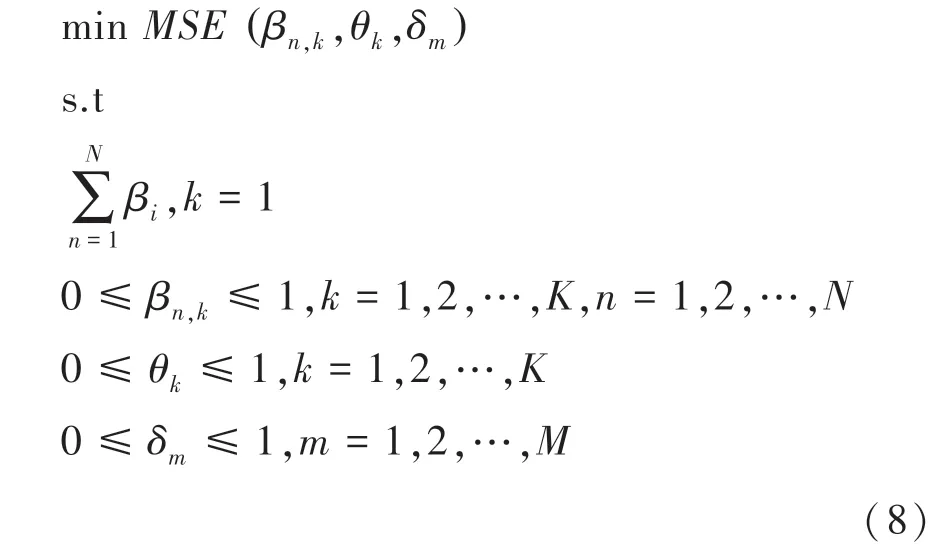
其中,N是在BRB 中设置的评估结果数;K是规则数目;M是前提属性数目。图1 对BRB 的优化流程进行了阐述说明。
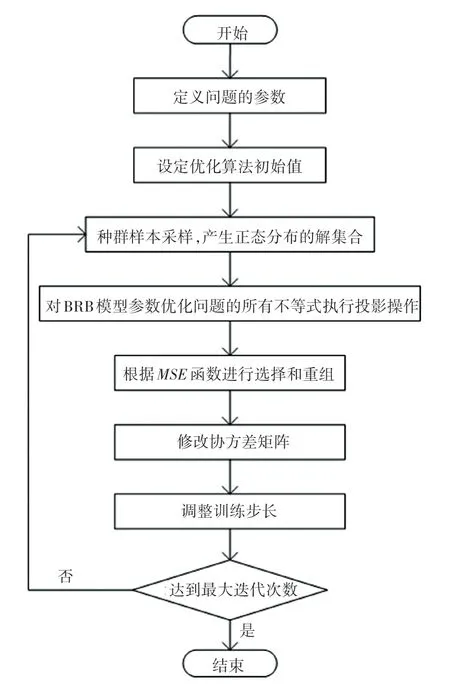
图1 BRB 参数优化流程Fig.1 BRB parameter optimization process
3 案例分析
3.1 实验定义
实验数据集为利用结构化建模获得的仿真数据集,其中包含距离、角度和评价结果,共480 个样本数据。随机选取其中240 个样本数据对模型参数进行优化,然后使用全部样本对BRB 模型建模效果进行测试。
3.2 模型参数设置
使用表示距离,表示角度,以这两个属性作为BRB 的前提属性。
距离包含4 个参考点:非常近(very near,VN)、近(near,N)、中等(middle,M)、远(far,F),可以表示为:
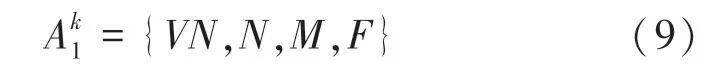
角度包含5 个参考点:优秀(Excellent,E)、好(Good,G)、中等(middle,M)、差(bad,B)、非常差(very bad,VB),可以表示为:
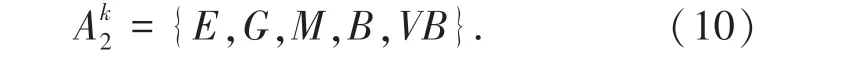
每个属性的每个参考点都有对应的参考值,距离的参考值以及参考点见表1,角度的参考值及参考点见表2。

表1 距离参考点和参考值Tab.1 Distance reference point and reference value

表2 角度参考点和参考值Tab.2 Angle reference point and reference value
让y表示BRB 的输出,其包含4 个参考点:优秀(excellent,E)、好(good,G)、一般(average,A)、差(bad,B),可以表示为:
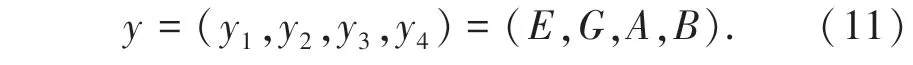
BRB 输出的参考点以及相应的参考值见表3。

表3 输出参考点和参考值Tab.3 Output reference point and reference value
初始置信表见表4。
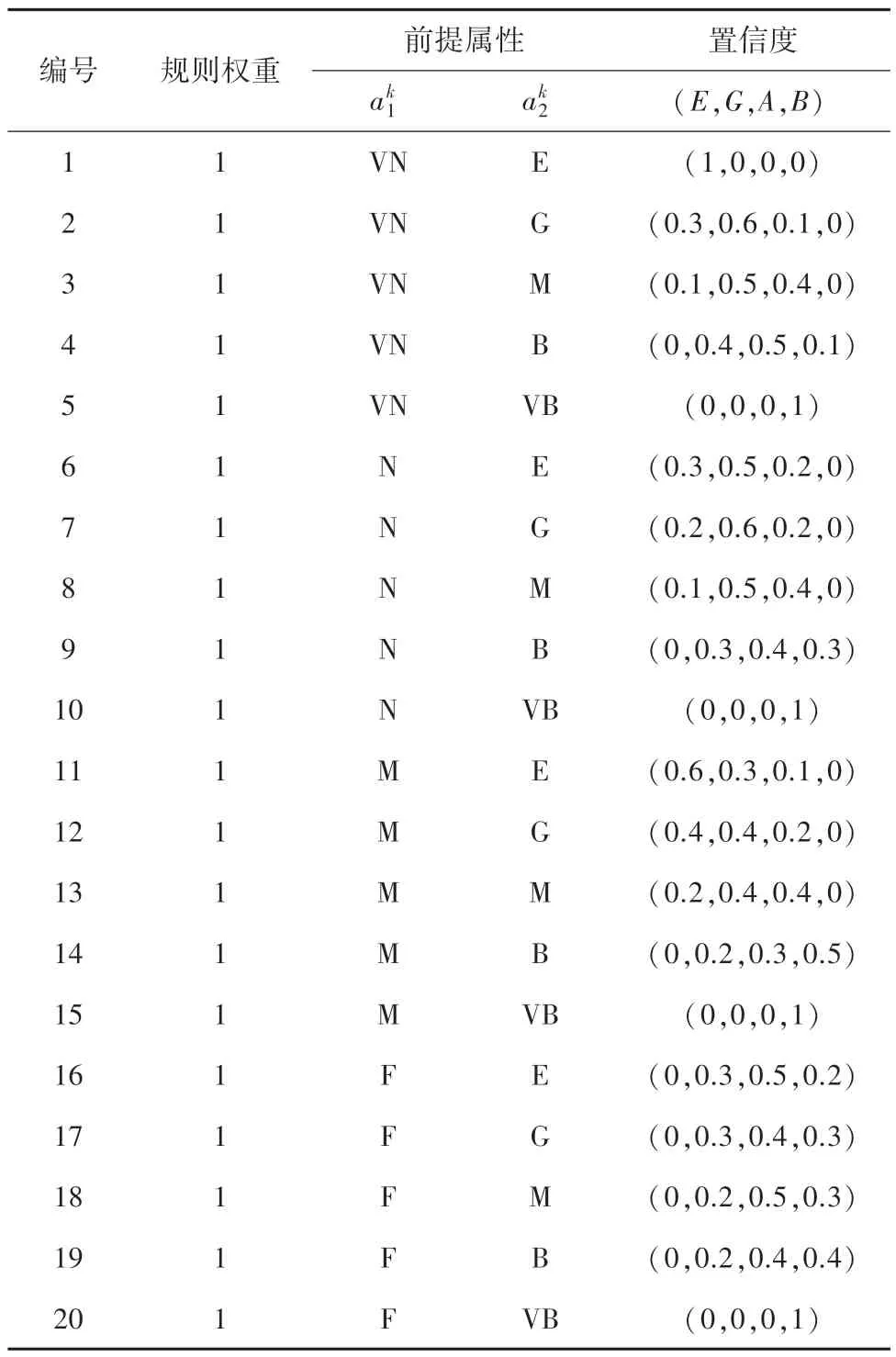
表4 初始置信表Tab.4 Initial belief table
3.3 实验结果
在给出初始模型参数后,使用训练数据集对BRB模型参数进行优化,然后使用测试数据集对模型进行测试。将BRB 输出结果与神经网络(Neural Network,NN)、模糊专家系统(Fuzzy Expert System,FES)、径向基函数(Radial basis function,RBF)和K 均值聚类(k-means)算法进行对比,拟合图如图2 所示。
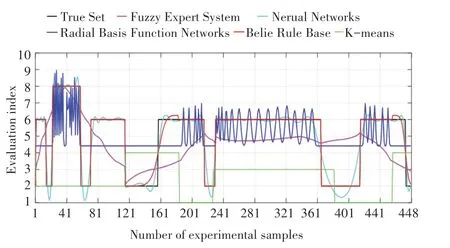
图2 拟合效果对比Fig.2 Comparison of fitting effect
对样本数据进行20 轮重复实验,然后计算个方法的平均MSE值(Mean Squared Error,均方误差),结果见表5。
由表5 可以看出,对于本次实验,相较于其他方法,BRB 的平均MSE值最低,建模效果最好。具体原因包含以下几个方面:

表5 MSE 对比Tab.5 MSE comparison
(1)神经网络、径向基函数和K 均值聚类等基于数据驱动的方法对数据具有较强的依赖性,在数据量较少时很难达到较好的建模效果。
(2)模糊专家系统等基于定性知识的方法仅依靠专家知识进行建模,然而专家知识中包含一定的模糊性以及不确定性,同时,由于该类方法不带有参数优化过程,因此建模效果一般。
(3)置信规则库可以有效融合定量数据与定性知识进行建模,在小样本情况下添加了专家知识的输入,同时可以对模型参数进行优化,因此具有较好的建模效果。
4 结束语
在本文中,提出一种新的基于BRB 的监控摄像机评价模型,该方法适用于多监控摄像机的调度问题。首先,根据专家知识建立BRB 模型初始参数,然后,通过实验数据对参数进行优化,最后,通过一个案例分析验证了该方法的有效性。该方法可以有效将定量数据与定性信息进行结合,有效地表示信息中的模糊不确定性和概率不确定性,并在模型中合理地对其进行处理,在工程实践中具有良好的应用前景。

