基于Flux 的故障IPMSM 仿真系统研究
柳波海,吴钦木,李志远
(贵州大学 电气工程学院,贵阳 550025)
0 引言
近年来随着电动车使用的增多,由其引发的交通安全问题也随之增多,而车用电机故障是造成电动车安全隐患的一个重要因素。据IEEE 工业应用协会关于电机可靠性调查结果[1]显示,每年电机的平均故障时间为几十到上百小时,严重影响了人们的正常生活和工作,因此对电机的故障诊断极其必要。目前,电动车的电机广泛使用内置式永磁同步电动机(IPMSM),其具有高效、高功率稠密、高可靠性和方便维护等优点[2]。IPMSM 进行故障建模时,其实物平台搭建成本较高,而改进绕组函数法[3]、等效磁路法[4]和有限元法[5]为主的电机建模方法成本较低且方便实现。
改进绕组函数法是一种电机电感的计算方法,该方法能考虑绕组参数及气隙数据的影响。文献[6]中对绕组函数进行理论推导,证明所提方法用于计算偏心电感的可行性;文献[7]提出了一种基于绕组函数理论(WFM)的电机建模方法。WFM 通过有限元方法(FEM)进行了改进,这种新方法具有良好的准确性且缩短了计算时间。但改进绕组函数法在建立电机模型时,需要忽略高倍频谐波及一些非线性因素的影响。等效磁路(MEC)就是将磁通在磁导体里通过的路径用磁路近似出来;文献[8]利用指数方程来考虑磁导率的非线性,磁极正对处的气隙磁通密度与有限元仿真结果相比误差较小;文献[9]使用磁通线创建了包括非线性磁阻的dq轴MEC。但在等效磁路电机模型中,需要考虑电机定子、转子和气隙的各部分磁路。如定子中齿和槽的磁路,绕组的磁路以及绕组周围空隙部分的漏磁路,转子中铁芯的磁路等。FEM 作为一种高精度的建模方法,常用于多物理量耦合场的分析计算;文献[10]中,基于FEM 分析了匝间短路(ITSC)故障对电磁参数的影响,分析结果可为DTP-PMSM 的ITSC 故障诊断提供参考;文献[11]提出PWM 逆变器馈电式永磁同步电动机的有限元分析(FEA),研究了匝数故障对机器参数的影响。
综上所述,为了方便计算,基于改进绕组函数和基于等效磁路的电机建模方法都需要一定程度地忽略掉齿槽效应、磁饱和等非线性因素的影响,从而降低了模型的精确度。而FEM 不仅不用忽略这类影响,还能考虑其他现实工况的影响,建立更精确的电机模型。因此,本文基于有限元法,对电机进行故障建模,并对电机驱动仿真系统进行研究,为电动车用电机故障诊断奠定数据基础。
1 Flux 故障电机建模
Flux 是一个有限元建模软件,常用于磁、电、热场的建模和仿真。Flux 广泛用于电机设计领域,如直流电机、感应电机、同步电机等。此外,Flux 的管理器中还集成了材料管理器、单位管理器和一些系统常用选项。使用Flux 建立电机模型的过程如下:
(1)建立电机几何模型;
(2)设置物理属性,其中包括材料设置、外部电路设计和机械属性设置;
(3)设置求解参数,对模型进行求解;
(4)处理求解结果。Flux 对每一步求解状态都保存了一个相应的文件,若要获取各个参数的求解结果,需执行“后处理”对结果进行可视化或保存。
电机故障主要分为3 类[12]:电气故障、机械故障及磁故障。本文以偏心故障和退磁故障为例,研究电动车用电机仿真系统。
1.1 静态偏心故障电机建模
由于偏心故障电机是一种非对称结构,因此,在Flux 中建立带偏心故障的电机时,需要设计电机机体的完整几何结构。如图1 所示,在建立IPMSM 几何模型时,需要在气隙设置时选择“ With Eccentricity”。在机械属性中可设置IPMSM 转子的旋转中心,进一步确定IPMSM 的偏心故障类型。

图1 Flux 中偏心故障电机设置界面Fig.1 Setting interface of eccentric fault motor in Flux
通过改变电机定子中心坐标,本文分别建立带有10%和20%的静态偏心故障的IPMSM。将10%偏心IPMSM 的定子中心坐标Or、转子轴心坐标Os设置为(0.06,0)和(0,0),使得|OsOr |为0.06 mm(均匀气隙长度g0为0.6 mm);将20%偏心IPMSM的定、转子轴心分别设置为(0.12,0)和(0.0),使得|OsOr |为0.12 mm。然后在机械属性中,将转子旋转中心设置为(0.0),使得转子旋转中心和转子轴心重合。
1.2 退磁故障IPMSM 建模
电动车用IPMSM 经常工作在空间狭小的高温环境中,且内嵌式的安装方式使得永磁体不易受车辆抖动而受损。因此,在电动车工况下,永磁体的退磁为均匀退磁居多,本文主要分析IPMSM 的均匀退磁故障。
在Flux 中,可通过“Linear magnetic described by theBrmodule”定义NdFEB 类永磁体。如图2 所示,设置“Remanent flux density”中的值,可定义永磁材料的剩磁Br;设置“Relative permeability”可定义磁性曲线的斜率。为了建立一个极对上永磁体带不同程度退磁故障的IPMSM 模型,本文定义3 条磁性曲线,分别为正常、25%和50%退磁材料的磁性曲线,如图3 所示。将正常永磁体的剩磁Br设定为1.2T,磁导率设定为1.05;25%和50%退磁的永磁体的剩磁Br分别设定为0.9T 和0.6T,而磁导率不变,矫顽力也相应变大。

图2 Flux 中线性特性的永磁体材料定义界面Fig.2 Permanent magnet material definition interface with linear characteristics in Flux
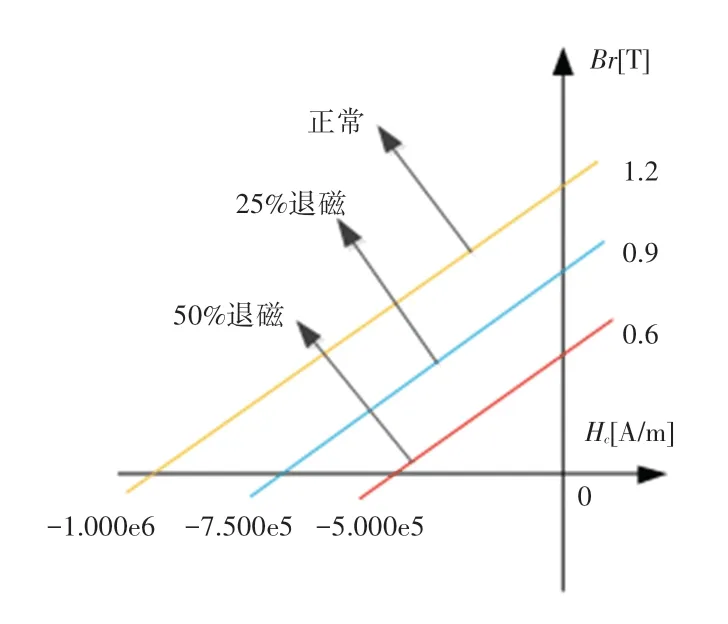
图3 NdFEB 材料及其退磁材料的磁性曲线Fig.3 Magnetic curve of NdFEB material and its demagnetization material
2 基于Flux 和MATLAB 的故障IPMSM仿真系统建立
本文利用有限元模型的精度和MATLAB控制算法的便利性优势,将Flux 建立的IPMSM 有限元模型嵌入到MATLAB-Simulink 环境中的矢量控制系统中进行在环实时分析。矢量控制系统中电流策略采用id =0,并且使用空间矢量脉宽调制(SVPWM)算法调制电机供电电压矢量,控制系统框图如图4 所示。Flux 和MATLAB—Simulink 联合仿真的IPMSM 有限元模型在环仿真系统结构框架如图5 所示。
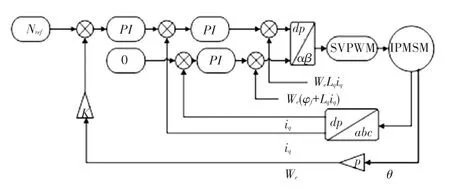
图4 矢量控制框图Fig.4 Vector control block diagram
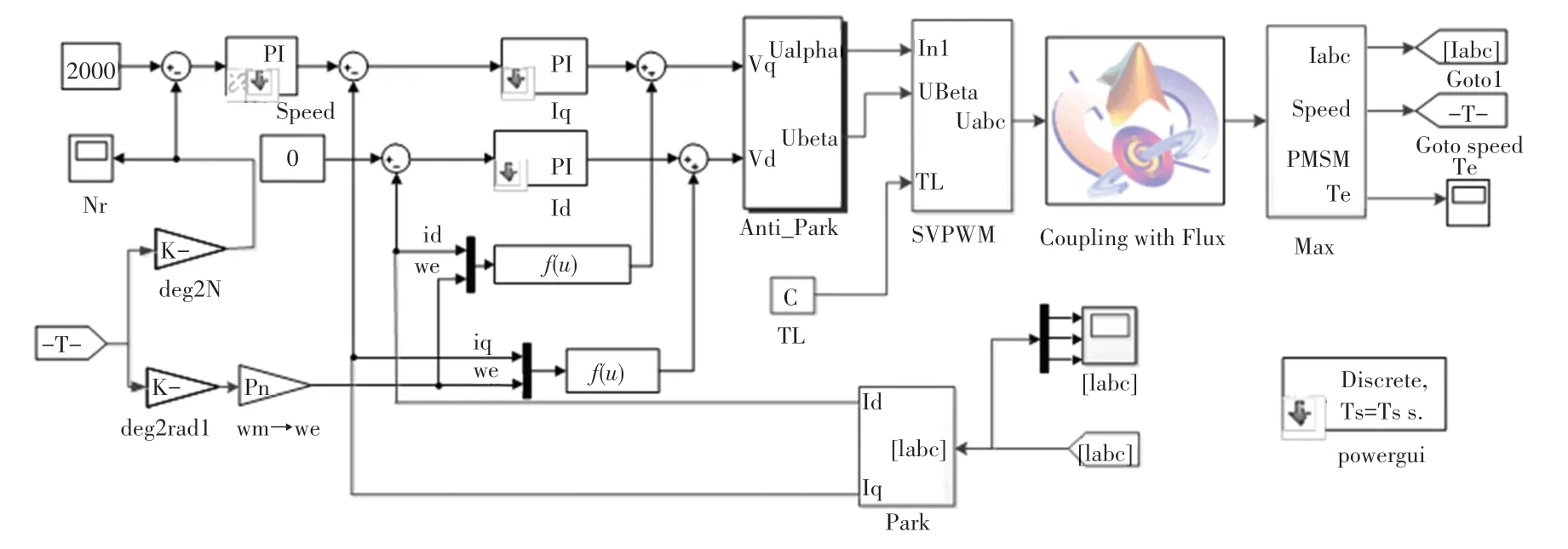
图5 Flux 和MATLAB-Simulink 的联合仿真系统图Fig.5 Co-simulation system diagram of Flux and MATLAB-Simulink
3 仿真结果分析
3.1 正常IPMSM 的联合仿真结果
取仿真步长a =1e-5,使用MATLAB 求解器FixedStepDiscrete,求解系统的控制部分。与此同时,将调制的SVPWM 信号输入到IPMSM 的有限元模型中,由Flux 迭代求解出电机状态并输出到Simulink 中,然后反馈到PI 控制器中形成闭环。为方便对比分析,对正常IPMSM 进行仿真,转速从0~3 000 rpm(空载),将不同转速对应的电流分别截取片段,如图6所示。其中包含:电机转速从1 000 rpm增加到2 000 rpm;转速从2 000 rpm增加到3 000 rpm;转速从3 000 rpm上升到3 060 rpm,再下降到3 000 rpm;以及稳定转速3 000 rpm 的运行状态。
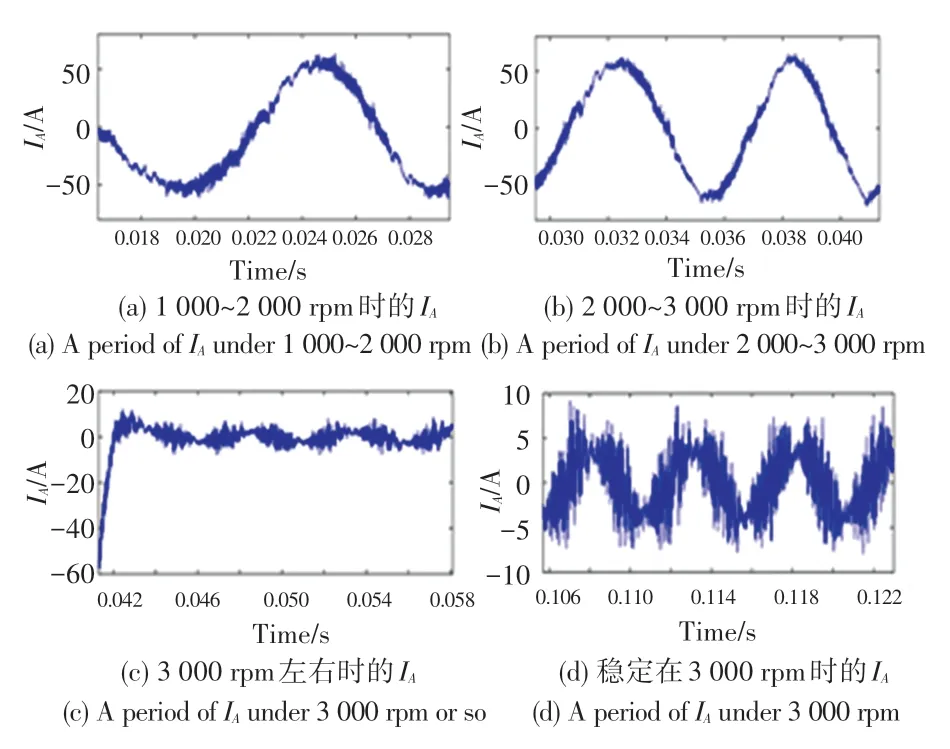
图6 正常IPMSM 在不同运行状态下的相电流波形Fig.6 Phase current waveforms of normal IPMSM in different operating states
3.2 退磁IPMSM 的联合仿真结果
遵从单一变量的法则,将一对极永磁体带有退磁故障的IPMSM 模型嵌入矢量控制系统中进行仿真分析。
采用同样的步长和初始状态,将带有25%退磁的IPMSM 嵌入矢量控制系统进行仿真分析。图7展示了25%退磁IPMSM 在不同运行状态下的相电流波形。
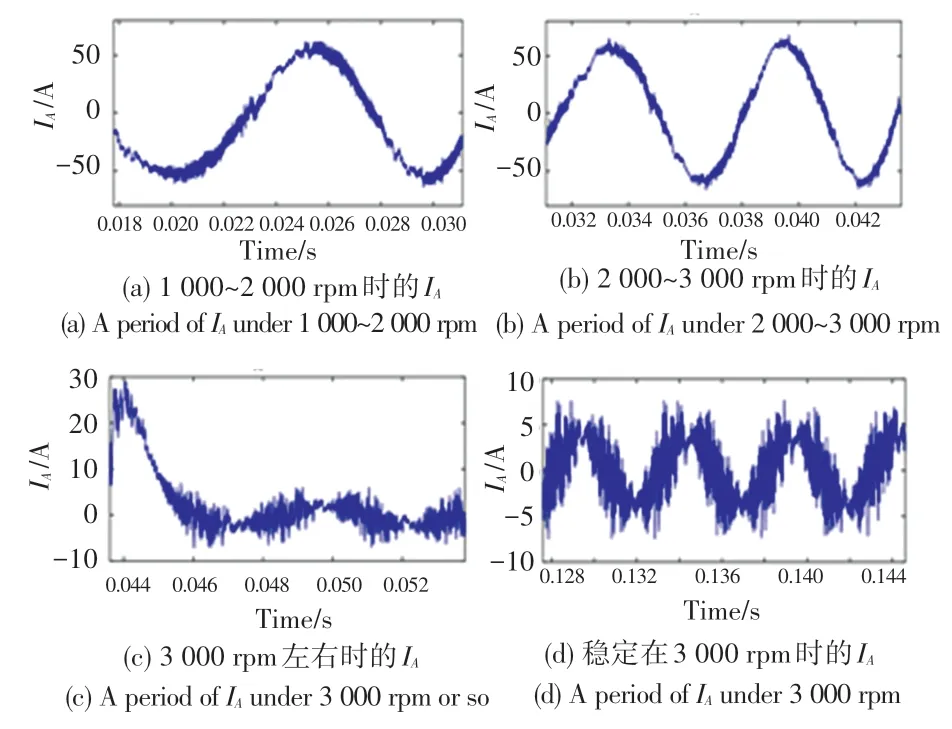
图7 25%退磁IPMSM 不同运行状态相电流波形Fig.7 25% demagnetization IPMSM phase current waveforms in different operating states
以同样的方法将50%退磁IPMSM 模型嵌入矢量控制系统中进行仿真分析,不同运行状态下的电流波形如图8 所示。

图8 50%退磁IPMSM 不同运行状态相电流波形Fig.8 50% demagnetization IPMSM phase current waveforms in different operating states
对比两种不同程度的退磁故障,由IPMSM 的相电流和正常IPMSM 的相电流可知,相同运行状态下,仅从波形形状上观察,两种故障电机的相电流与正常电机几乎没有差别。但从电流幅值减小的过程来看,退磁故障电机的电流幅值达到稳定的时间比正常电机更长。正常电机在仿真时间为0.042 s 时电流幅值已经下降至0 附近,而存在25%退磁故障的IPMSM 电流,在0.046 s 下降到0 幅值附近,含50%退磁故障的IPMSM 需要0.048 s 下降到0 幅值附近。由此可知,退磁故障降低了电机的输出转矩,相当于增加了电机负载,因此使得电机转速从启动到稳定时的时间增加。
3.3 静态偏心IPMSM 的联合仿真结果
同样遵从单一变量的法则,分别将10%和20%静态偏心故障电机模型导入MATLAB-Simulink 中的矢量控制系统,采用同样的仿真步长及初始状态进行仿真分析。图9 和图10 分别展示了含10%偏心故障IPMSM 及含20%偏心故障IPMSM 在不同运行状态下的电流波形。
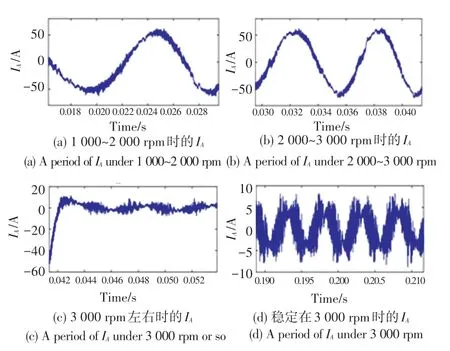
图9 10%偏心IPMSM 不同运行状态相电流波形Fig.9 10%eccentric IPMSM phase current waveforms in different operating states
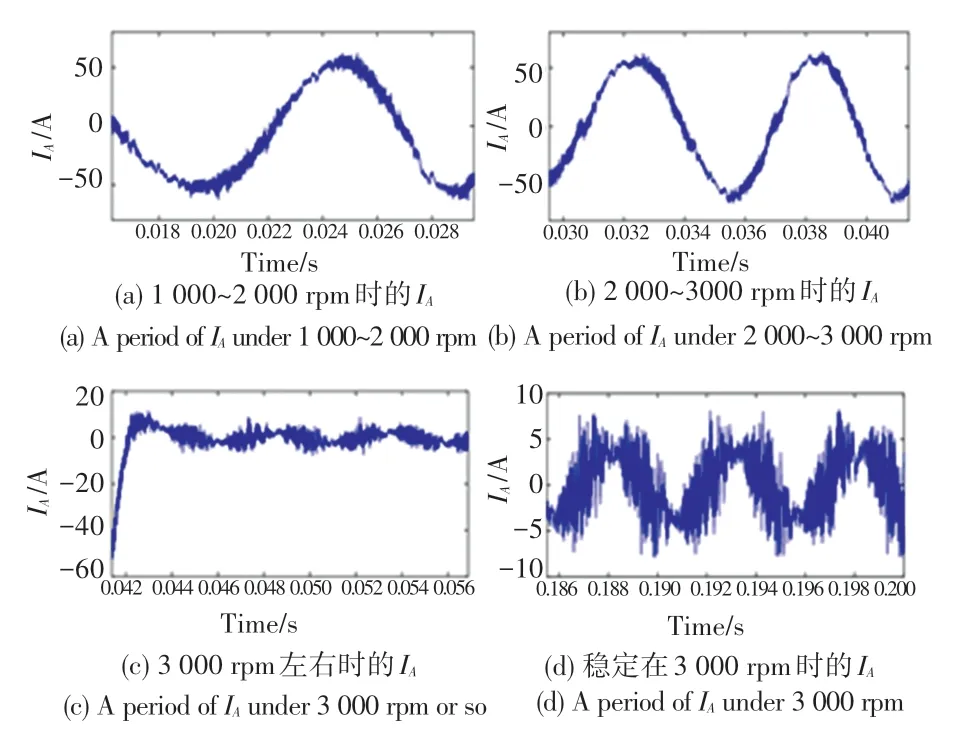
图10 20%偏心IPMSM 不同运行状态相电流波形Fig.10 20% eccentric IPMSM phase current waveforms in different operating states
对比图9、图10 和图6 可知:在时域上,纯静态偏心故障对电机相电流影响较小。
4 结束语
本文研究了一种基于有限元软件Flux 和MATLABsimulink 的电动车用电机联合仿真系统,将各种IPMSM 有限元模型嵌入到MATLAB-Simulink 的矢量控制系统中,对各个IPMSM 模型进行联合仿真,仿真结果表明:与正常电机相比,当电流幅值减少时,永磁体退磁程度越大,电流达到稳定所需的时间就越长;但对于电机含有偏心故障,对电机相电流的影响非常小,转速达到稳定所需的时间相差较小。根据以上电机的数据,能为电机的故障诊断奠定数据基础。

