巧搭助学支架,促进学生深度学习
吴煌

支架式课堂教学,是指老师在课堂中以学生为主导,以学生已有的知识水平为基础,给学生创造一个有效掌握和了解新知识点的“支架”。本文以“勾股定理复习课”为例,研究了老师怎样立足学生的思维最近发展区,为掌握好知识点概念的生长路线和重要节点搭建助学支架,并注重学生思维的建立与思维的生长,使学生在学习支架的指导下以小坡度慢慢生长,从而逐步掌握知识点,进而深入学习。
一、教学过程概述
(一)搭建实景支架,激学导思
导学1:已知区知识回顾
(1)在三角形ABC中,其中两边AC、BC分别为3cm 和4cm,那么AB的长为 .
(2)在直角三角形ABC中,其中两直角边AC、BC分别为3cm和4cm,则AB的长为 .
(3)在直角三角形中,其中两边AC、BC分别为3cm和4cm,那么AB的长为 .
设计意图:在勾股定理的使用易错点和技巧上设置了三道抢答题,帮助学生建立有价值的知识框架。深度复习了勾股定理的文字叙述及几何语言,考察三角形第三边的取值范围,理解数字和图形结合这一数学思维和分类讨论的数学思维,为后面的深入学习做好铺垫。
导学2:新课学习
框架式导向助学支架:
设计意图:搭建框架式导向支架,引导学生探究,使其懂得在做题中抓大放小。三种思想就是本节课的支架,是授课的主线,三种思想方法的领悟与技巧学习也是本节课的学习目标。
(二)搭建范例及问题变式支架,以学推思
探究环节一:勾股定理中的分类讨论思想
例1一个直角三角形的三边长分别为6cm,4cm,Mcm,那么以M为边长的正方形的面积为 .
变式:在等腰三角形ABC中,已知AB=AC=7,△ABC的面积为17,则BC= .
【问题串助学支架1】
1.数字与图形结合的新题型,你感悟到什么数学思想?
2.除了数形结合思想,你还从中感悟到什么数学思想?
3.勾股定理运用中,直角边与斜边不明时需要分类讨论,角不明的时候怎么分类讨论?
设计意图:例子是老师故意设立的支架,目的就是要学生通过相互合作,理解本题解题的关键就是合作探讨,通过变式训练,对分類讨论思想再领悟,深认识,实现深度学习;最后梳理出勾股定理中分类讨论的技巧:1.直角边与斜边不明需分类讨论;2. 锐角或钝角三角形形状不明需分类讨论。
探究环节二:勾股定理中的方程思想
例2 一个直角三角形,一直角边是6,斜边长比一另条直角边大2,斜边长是 .
变式1:如图,在△ABC中,AB=6,BC=4,AC=3,求△ABC的面积.
【问题串助学支架2】
1.已知三角形的边,求三角形的面积,则需要求三角形的哪个元素?
2.添加辅助线,你发现了什么特殊三角形?它们之间关系如何?
3.感悟方程思想,合作探究变式1。
变式2:如图,将长方形ABCD沿边EF折叠,使点C落在AB边的中点C′上. 若AB=12,BC=18,求BF的长.
【问题串助学支架3】
1.折叠前后的图形,边长有何关系?
2.找出已知两边关系和第三边的长的直角三角形。
3.对于例2的解题方法,是否可以运用到本题中?
4.利用勾股定理解决折叠问题,你有什么方法技巧?
设计意图:以例2为支架,进而理解如何解方程。然后,再以此为支架,探索通过作高,将斜三角形转化成直角三角形,巧妙利用公共边相等这一桥梁,结合勾股定理列方程求线段长以及折叠问题中结合勾股定理列方程求线段长的技巧,实现深度学习如何在勾股定理中利用方程思想方法解决问题。
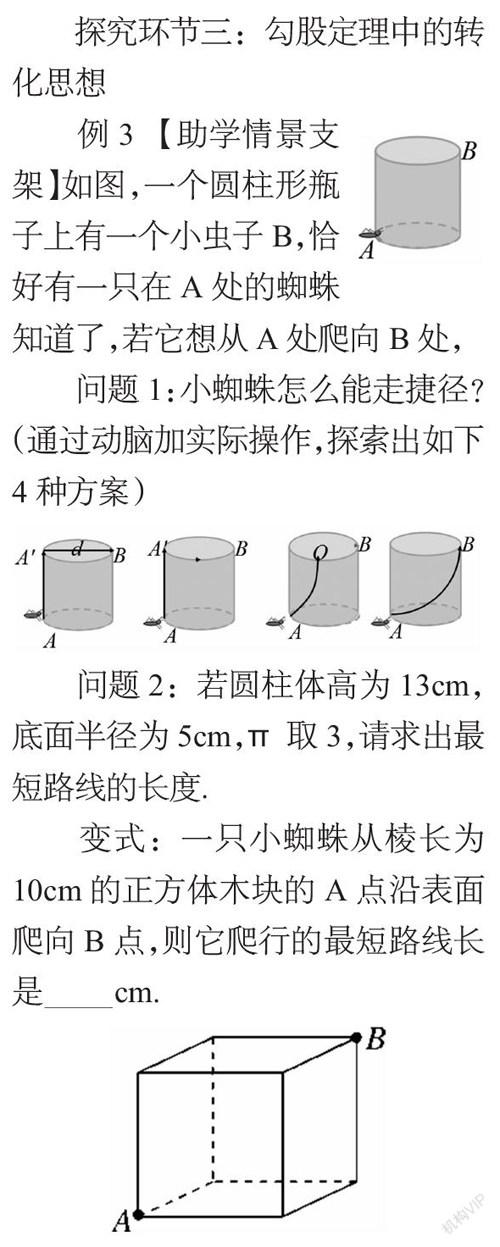
探究环节三:勾股定理中的转化思想
例3 【助学情景支架】如图,一个圆柱形瓶子上有一个小虫子B,恰好有一只在A处的蜘蛛知道了,若它想从A处爬向B处,
问题1:小蜘蛛怎么能走捷径?(通过动脑加实际操作,探索出如下4种方案)
问题2:若圆柱体高为13cm,底面半径为5cm,π取3,请求出最短路线的长度.
变式:一只小蜘蛛从棱长为10cm的正方体木块的A点沿表面爬向B点,则它爬行的最短路线长是 cm.
设计意图:搭建出情景这一支架。使得枯燥的数学教学增添一定的趣味性,进而提高学生解决实际问题的能力。通过动手操作,领悟到勾股定理用转化思想求最值问题的技巧。通过变式训练进一步熟悉二、三维图形的转化思想,内化学生的解题图式,实现深度学习。
(三)搭建总结评价支架,因学会思
1.本节课学习的勾股定理,请大家告诉我有哪些数学思维蕴含其中?
2.通过运用勾股定理,可以分析出使用了哪些数学思维方法中的技巧?
3.以知识核心,思想为主线,技巧为依托,画出本节课的思维导图。
4.从数学练习册中找出分别使用到以上数学思想的习题,并做方法标识。
设计意图:通过搭建一个总结助学支架,让全体学生认真梳理本次课程的学习要点。本环节可以给学生们提供一个更大的思考和发展时间,把自己的课内知识扩散延伸至课外,意在促进本节课知识和策略的应用,促进知识及思想方法的灵活迁移,进而实现深度学习的目的。
二、教学总结与思考
(一)搭建情境化支架,引发学生自主学习
课堂教学中我们要严格遵循小学生认知和发展的规律,围绕课堂教学内容来创造一些富有挑战性和具有探究精神的问题,引领小学生走向问题,将浅层的思考方式转化成一种深度的设疑,为小学生进行深度学习搭建了舞台,提供一个深度理解的机会。
(二)搭建数学思想方法主支架,锁定学习目标
在课堂教学中,我们一定要根据实际情况,站在一个能够使全体同学深刻感悟的数学基础理念的角度设计问题系列,引导学生在理论与实践中探索与分析所要解决的问题,掌握所需要学习的数学基础知识,形成自己的一些数学基础技能,逐步完成并达到课标(2011年版)中所明确提出的教学总目标。
(三)巧搭螺旋助学支架,催生学生思维的自然生长
找准学生的知识起点,厘清了学生的现有水平及潜在发展区,目的就是要及时唤醒与新知识有关的旧知识,实现学生思维的自然生长。本节课搭建了阶梯式螺旋上升的助学支架,催生学生思维的自然生长。
第一环:搭建知识范例支架,帮助大家完善知识结构,理清知识内部联系与结构,进而达到实现思维联通透彻的目的。通过搭建范例支架,落实学生的最近发展区,明确学生将要探究什么样的知识,感悟哪些数学的思想方式,提升哪些数学课程中的核心知识素养,促进学生的思维真正在其中发生,为深度学习提供了沃土。
第二环:老师通过设置问题串式向导支架,在教学活动中不断地采用具有启发性的提示语和问题作为支架,来启发和激活学生的思维,调动学生自主探索和学习的积极性,引导学生不断寻找解決问题的思路,总结各个例题的解决方法和技巧,寻求问题发展及解决的过程, 使学生的思维得到了小坡度、螺旋式的自然生长,慢慢走向深度学习。
第三环:搭建一个可以把问题转化的支架,引领每一个小组的学生一步步进行探究,主动获取所需要探索的知识,分析和解决一系列的问题。学生们可以通过自己解决实际问题来巩固所掌握的知识,变被动学习为主动学习,促使知识融会贯通,不断拓展思维的深度和广度,提升思维品质和数学素养,从而实现深度学习。
(四)巧用支架的“留白”策略,提升学生的自主学习能力
教师应该要做到尽可能在时间、内容、评价上给学生留白,营造良好的环境和氛围,激发他们的兴趣和情绪,促使他们自己走出来亲身体验,学习支架的建立和展开中要充分地通过对于空白的建立和展开,调动学生思维的主动性与积极性。
责任编辑 钱昭君

