基于改进普氏平衡拱理论的层状顶板安全厚度研究
罗 霄
(1.中煤科工生态环境科技有限公司,北京 100013;2.天地科技股份有限公司,北京 100013;3.煤炭科学技术研究院有限公司 安全分院,北京 100013)
0 引 言
工程资料表明,围岩的变形破坏不能忽略水平地应力的影响,特别针对采空区或巷道顶板为坚硬岩层或层状岩层时,传统的普氏平衡拱理论不能客观反映层状顶板的冒落特性和破坏状态。传统普氏平衡拱的理论是建立在松散介质的基础上,认为硐室开挖后上覆岩层由于节理的切割而处于松散状态,在均布荷载的作用下,地下硐室的滑裂面出现在侧壁处,硐室顶部中央的应力最大。过去,在露天矿区我国很多井工矿长期采用房柱式方法进行开采,而形成许多大小不一、形态各异、层位复杂的采空区[1]。同时,由于资料欠缺与不完善,无法准确确定采空区位置和边界,给安全生产带来重大隐患[2]。
在采空区顶板成拱理论方面,国内外学者做了大量研究。钮新强等[3]对三峡工程地下厂房硐室围岩顶拱承载力学作用机理进行了深入研究,提出了“稳定拱”概念,确定了地下硐室稳定拱的力学边界条件,验证了稳定拱结构确定上覆岩体安全厚度的可行性;姜立春等[4]通过构建采空区顶板跨度与冒落高度双因素耦合下的三铰拱力学模型,推导出顶板拱最大轴向应力解析式,验证了采空区顶板拱架自稳效应。黄庆享等[5-6]提出了巷道围岩自稳平衡圈理论、极限自稳平衡拱理论、自稳隐形拱理论及“拱梁”结构理论,并推导相应理论的曲线方程;鲁岩等[7]从水平应力作用特征角度出发,深入分析巷道周边自稳结构的外观形态,推导出了修正普氏平衡拱的稳定平衡方程。马文强等[8]在观测再生顶板“三带”高度基础上,建立及推导出巷道再生顶板修正普氏平衡拱模型、方程及矢高解析式。
尽管国内外学者对传统的采空压顶板成拱理论进行了不断修正与改进,取得了一定的进步,但其所得成果应用于井工煤矿层状顶板条件时,与实际结果存在一定差距。为此,作者基于层状顶板逐层冒落的工程特点,并考虑水平侧压力影响,对不同工况下采空区层状顶板成拱机理进行探讨,改进普氏平衡拱理论计算公式,为合理预测采空区顶板安全厚度提供一定的参考依据,为露天矿区井工矿采空区治理提供理论指导。
1 层状顶板变形破坏特征分析
井工矿采空区开挖卸载后打破了围岩的原岩应力平衡状态[4]。由于采空区顶板逐渐冒落,顶板的承载结构随之发生改变,即由梁承载结构转变为拱形承载结构,顶板上的拉应力逐渐转为沿着拱轴方向的压应力[3,9],最终形成形态各异的平衡拱[10]。
采空区顶板一般由多层相间的软弱岩层构成,其主要特征表现为层状岩层自稳性能差[11],岩性不一致,整体稳定性弱、强度低且松散易碎,岩层之间多存在弱面,分层或冒落时有发生。层状顶板的变形破坏过程通常包括3个阶段:
1)井工矿采空区形成后,顶板原岩应力重新分布,采空区两侧的受力状态由三向受压变为两向受压之后,顶板岩层将步入弹性变形阶段,产生一定程度的挠曲变形,层与层之间的弱结构面会出现不同程度的剥离[12]。
2)当垂直荷载和水平荷载共同作用于顶板,使顶板应力不断得到释放,挠曲变形会进一步加剧,软弱夹层则发生渐进式破坏,在顶板跨中处开始出现裂纹。与此同时,在采空区两帮与顶板肩部位置处的岩体所受压应力高度集中,最终由于压应力及应变过大而导致帮部岩层出现片帮滑落,形成不同形式的片帮,失去承载上部顶板的能力[13]。
3)随着顶板下部岩层的进一步拉裂和帮部岩体片帮,顶板各岩层在垂直地层荷载作用下挠度越来越大,顶板各层岩体的裂纹迅速扩张、贯通直至最终破坏,从而使顶板岩体逐层向上垮落形成不同形态和拱高的平衡拱[14]。
采空区顶板各层岩性及厚度均存在一定的差异,各层岩体显现出明显的各向异性,顶板破坏规律表现为:①在垂直荷载和水平荷载的共同作用下,顶板最下部岩层开始变形破坏直至冒落,直接影响紧邻其上岩层的稳定性,且上部岩层的跨距即为下部岩层垮落后的宽度;②采空区的跨度直接影响其顶板形成的冒落拱拱高,在形成的平衡拱拱高中占主导地位;③冒落拱的变化发展是由顶板下部岩层逐层向上冒落,且各岩层形成的冒落拱形状和高度各不相同。
2 传统普氏平衡拱理论存在的问题与改进
2.1 传统普氏平衡拱理论的问题
20世纪初,普氏平衡拱理论是由俄罗斯人普罗托奇雅科诺夫依据散体结构岩体提出,认为在巷道或采空区初步形成后,由于垂直地层荷载作用于顶板上,致使岩层逐渐冒落形成拱带,采空区上方部分岩体荷载由拱自身承担。该理论仅适用于强风化的松动破碎岩体和新近堆积的土体。
对于较坚硬岩体的采空区而言,顶部受到垂直地层荷载的压力,侧帮不会受压,从而形成自然平衡拱;对于较松软岩体的采空区而言,其顶部同样受到地应力作用,使侧帮倾向于片帮,进而形成压力拱。
尽管普氏平衡拱在一定程度上客观反映了地下硐室顶板冒落的实际情况,对实际地下工程顶板的有效支护具有一定的参考价值,在工程实际中得到了长期广泛的推广应用。然而,对于矿山采空区层状顶板的变形破坏,该理论在条件假设方面和分析推导过程中仍然存在如下3个方面的不足[12]:①水平构造应力对顶板平衡拱的影响没有考虑:虽然水平方向的构造应力作用较垂直方向自重应力作用小,但是水平方向的构造应力对采空区顶板下部的破坏仍然有较大影响,且直接关系到顶板的安全厚度计算问题[14];②采空区或巷道帮部片帮形式的多样化没有考虑;③层状顶板逐层冒落的实际工程特点没有考虑。
2.2 顶板平衡拱理论的改进
基于层状顶板逐层冒落的工程特点,建立层状采空区顶板在水平构造应力和垂直地层荷载联合作用下的平衡拱力学模型,如图1所示[15-16]。

1—自然平衡拱;2—隐形平衡拱;3—扩展隐形平衡拱;λ—水平侧压系数;q—上覆岩层荷载;h—采空区高度;a—跨度的1/2图1 复合层状顶板平衡拱力学分析模型Fig.1 Mechanical analysis model of balanced arch of composite layered roof
初始自然平衡拱[17]是在采空区形成过程中,顶板冒落至某一阶段时出现的。若对顶板处理不及时,则初始自然平衡拱将会逐渐垮落形成极限自然平衡拱,如图2所示。
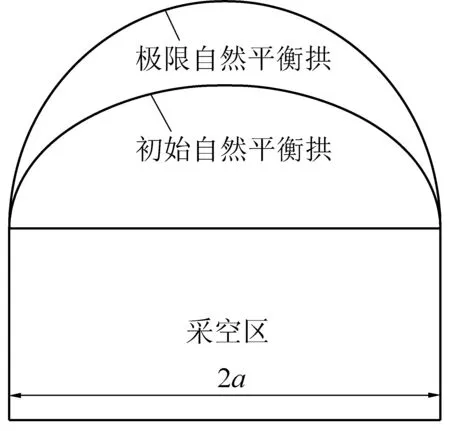
图2 不同稳定状态下的顶板平衡拱形态Fig.2 Shape of balance arch of roof under different states
若采空区帮部发生片帮失稳,其有效跨度则会进一步扩展。此时,层状顶板极限自然平衡拱将进一步演变为隐形平衡拱和扩展隐形平衡拱。因此,需要计算极限自然平衡拱中扩展隐形平衡拱的拱高,才能对采空区顶板的极限安全厚度进行估算。为了方便进一步研究,将层状顶板垮落形成的平衡拱轨迹线简化为光滑曲线,并对极限自然平衡拱特征进行深入分析。
2.2.1 极限自然平衡拱的形态及拱高分析
由于平衡拱的对称性[18],建立极限自然平衡拱左半部分力学模型进行分析[19],如图3所示。
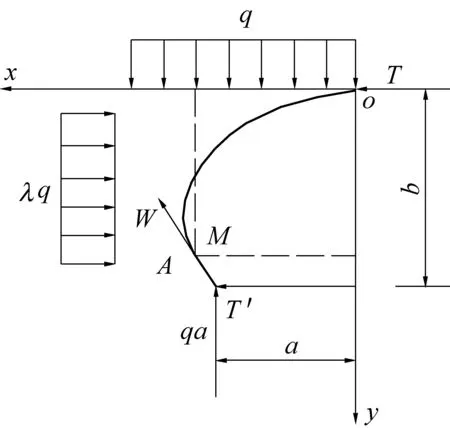
W—水平切力T′与垂直应力qa的合力图3 极限自然平衡拱计算模型Fig.3 Calculation model of ultimate natural equilibrium arch
在极限自然平衡拱拱线上任取一点M(x,y),对其进行受力分析可得如下平衡方程为
Ty-qxx/2-λqyy/2=0
(1)
式中:T为平衡拱拱顶处所受水平方向上的切力。
左半拱沿水平方向静力平衡式为
T-λqb+T′=0
(2)
式中:b为自然平衡拱拱高;T′为拱脚所受水平切力。
由拱脚平衡可得
KT′-qaf=0
(3)
式中:K为稳定平衡拱拱脚的安全系数;f为岩石的坚固性系数或普氏系数,一般取f=R/10,R为岩石单向抗压强度。
将式(2)和式(3)代入式(1)得
x2+λy2-2(λb-af/K)y=0
(4)
下面对不同侧压系数下极限平衡拱的形态及其拱高进行讨论。
1)当λ=0时,由式(4)得
(5)
式(5)为抛物线方程,其与没有水平侧压力条件下的普氏自然平衡拱相似,其中af表示负方向的矢量。将x=a,y=b,K=2代入式(5)得
(6)
式(6)与普氏理论所得结论相吻合。
2)当0<λ<1或λ>1时,将式(4)简化,得
(7)
且
式中:m为椭圆中心y轴坐标。
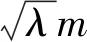
(8)
将x=a,y=b代入式(4)得
(9)
式(9)是关于极限平衡拱拱高b的二次方程,解之得
(10)
进而得到
(11)
通过式(11)分析可得,拱高b与稳定平衡拱拱脚的安全系数K有关系,随增大而减小,拱脚处就会越来越稳定。
3)当λ=1时,由式(7)得
x2+(y-m)2=m2
(12)
这是一个圆的方程,圆心(o,m)在顶板AB的上方,与顶板AB的距离d为
(13)
令式(13)中λ=1,即得到极限自然平衡拱为圆弧拱时的拱高为
(14)
由式(14)可知,处于静水压力状态(即λ=1)的矿山采空区围岩,当其拱脚处的普氏系数f和稳定安全系数K一定时,平衡拱拱高与采空区半宽成正比例关系。
2.2.2 隐形平衡拱和扩展隐形平衡拱的形态
在露天矿推过井工采空区的实际工况中,经常发生采空区帮部失稳,失稳后的有效跨度如图4所示[18]。此时,层状顶板自然平衡拱将进一步演变为隐形平衡拱和扩展隐形平衡拱。
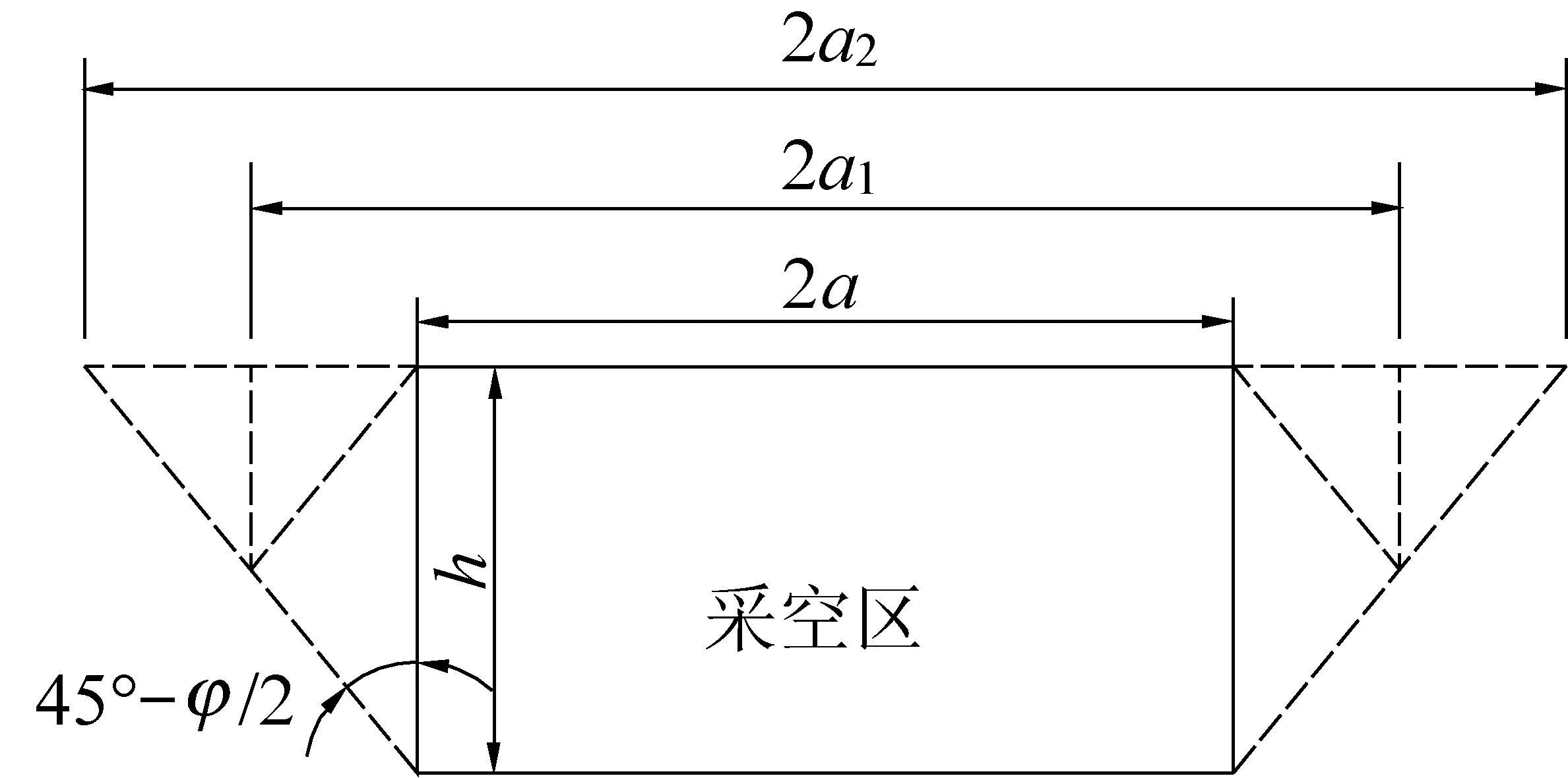
图4 采空区在不同平衡拱下的有效跨度Fig.4 Effective span of goaf under different equilibrium arches
由理论推导及力学分析可得层状顶板隐形平衡拱和扩展隐形平衡拱的采空区有效跨度为
(15)
式中:a1为帮部失稳后形成隐形平衡拱的半跨度;a2为帮部失稳后延伸形成隐形平衡拱的半跨度;φ为岩石内摩擦角。
2种平衡拱形态及拱高分析方法类似,对扩展隐形平衡拱的形态和拱高具体分析如下:
1)当λ=0时,由式(6)和式(15)得
(16)
式中:b1为扩展隐形平衡拱的拱高 。
式(16)同样与普氏理论所得结论相符合。
2)当0<λ<1或λ>1时,由式(4)、式(9)和式(15)得
(17)
式(17)是关于扩展隐形平衡拱拱高b1的二次方程,解之得

(18)
由式(18)可知,当其他参数一定时,层状顶板的平衡拱拱高与采空区高度、水平侧压力和采空区跨度密切相关。即:高度和跨度不变,拱高随侧压系数的增大而减小;当侧压系数一定时,采空区的高度或跨度越大,层状顶板平衡拱的拱高就越高,对应采空区顶板安全厚度就越大。
在式(18)中,b1求对K的导数得
(19)
由式(19)可知,拱高b1随安全系数K的增大而减小。
3)当λ=1时,由式(4)、式(9)和式(15)可得扩展隐形平衡拱为圆弧拱时的拱高为
(20)
由式(20)可知,处于静水压力状态(即λ=1)的矿山采空区围岩,当其拱脚处的普氏系数f和稳定安全系数K一定时,平衡拱的拱高与采空区半宽仍然成正比例关系。
改进的普氏平衡拱理论适用于较破碎性岩体稳定分析计算(倒置漏斗型及复杂型采空区),但在岩石普氏系数f<0.8,采空区上覆岩体厚度小于采空区扩展隐形平衡拱的拱高时,由于其本身不能形成压力拱,所以改进的普氏平衡拱理论并不适用采空区顶板安全厚度的计算与确定。
3 工程应用实例
3.1 工程概况
选取某露天矿区某矿6022工作面和6039工作面为实例。2个工作面皆位于6煤层内,采空区围岩加权内摩擦角φ约为33°,设普氏系数f=1.9,稳定平衡拱拱脚的安全系数K=2,6022工作面埋深264 m。根据以往现场进行的地应力测量,侧压系数为0.5。
3.2 传统普氏平衡拱理论计算分析
根据李地元等[20]的研究结果,用未改进的传统普氏平衡拱理论计算的平衡拱拱高的2倍即为采空区顶板的安全厚度。计算公式为
(21)
式中:H0为压力拱高度,m;φ为岩石内摩擦角,(°);L为采空区跨度,m;H为采空区高度,m;f为普氏系数,取f=R/10,R为岩石单轴抗压强度,MPa。
设采空区高度为4、6 及8 m,由未改进的传统普氏平衡拱理论计算不同采空区高度条件下安全顶板厚度及厚度变化曲线,见表1和图5。
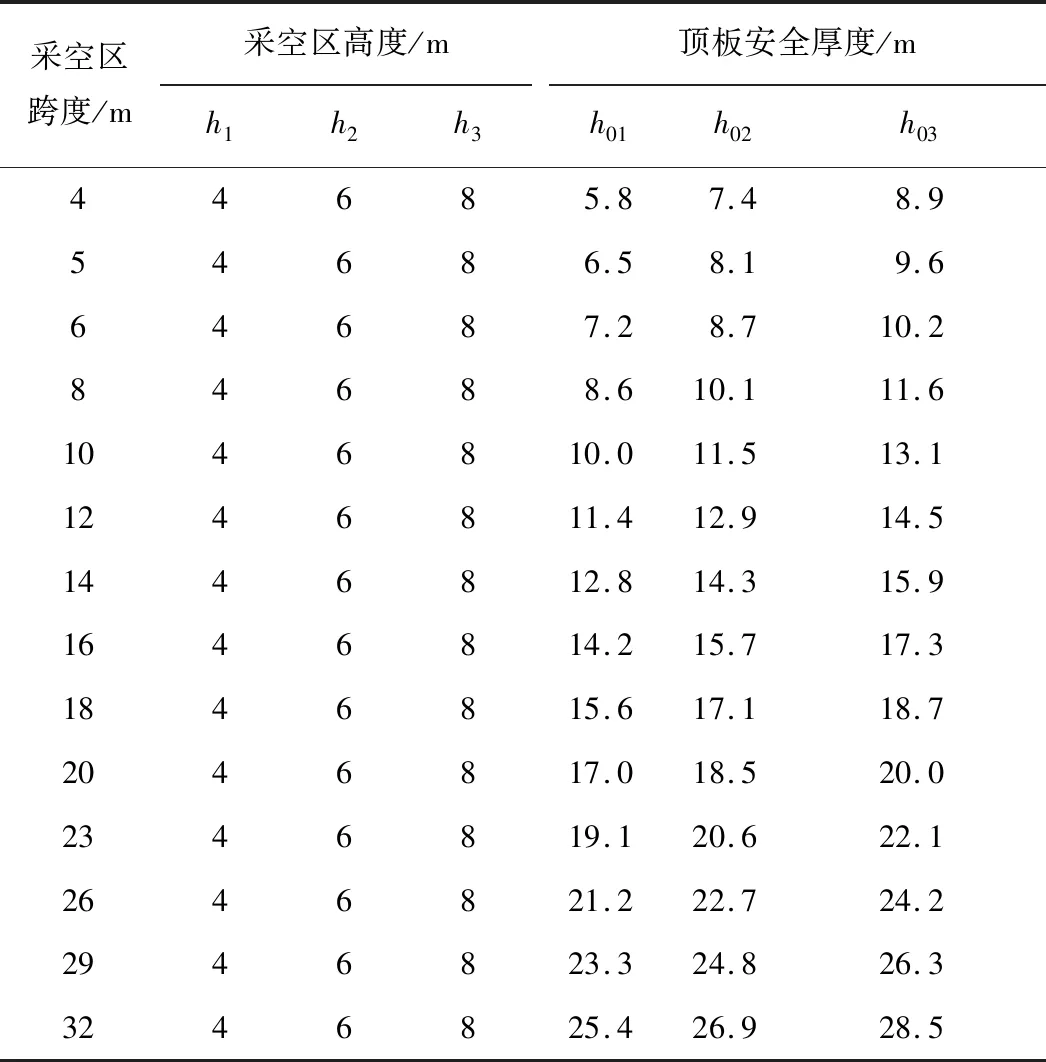
表1 原普氏平衡拱理论计算采空区安全厚度 Table 1 Calculation of safe thickness of goaf by original Protodyakonov equilibrium arch theory
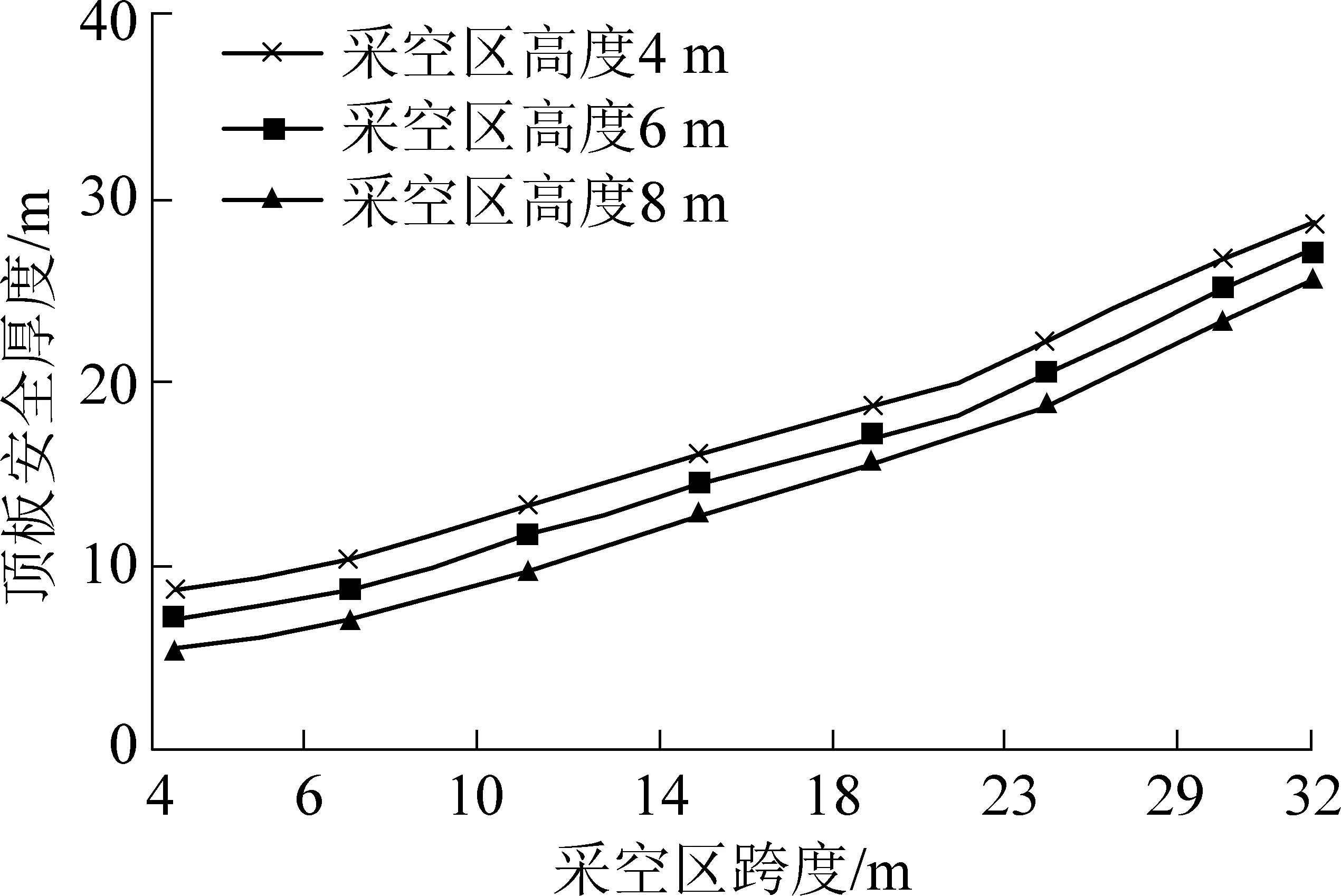
图5 不同采空区高度条件下顶板安全厚度变化曲线(未按改进普氏平衡拱理论计算)Fig.5 Variation curve of safety roof thickness under different goaf height conditions (Protodyakonov equilibrium arch theory method unmodified)
从表1和图5中可以看出,当采空区的跨度越大,顶板的最小安全厚度虽然在增大,但是增大幅度较小,这明显与实际工况相违背。
传统普氏平衡拱理论估算法受普氏系数影响尤为严重,根据经验来选取压力拱上方稳定岩层厚度等于压力拱拱高,最终用2倍的拱高来估算露天矿采空区顶板最小安全厚度存在显著缺陷。
3.3 改进普氏平衡拱理论计算分析
通过上文分析可知露天矿井工采空区顶板的拱高与水平侧压力有关,而地球构造应力决定了地下采空区水平侧压力的存在性,采用改进的普氏平衡拱理论,克服了原平衡拱理论计算存在的局限性。
以6039工作面采空区为例,设采空区高度为4、6及8 m,将各参数代入改进后的普氏平衡拱理论计算公式(18)中,得到采空区顶板安全厚度计算表,见表2。采用改进的普氏平衡拱理论计算法确定的不同采空区高度条件下顶板安全厚度变化曲线如图6所示。

表2 改进普氏平衡拱理论算法确定采空区顶板安全厚度 Table 2 Calculation for determining thickness of safety roof in goaf by improving theory algorithm of Protodyakonov equilibrium arch

图6 不同采空区高度条件下安全顶板厚度变化曲线(改进普氏平衡拱理论)Fig.6 Variation curve of safety roof thickness under different goaf height conditions(improved Protodyakonov equilibrium arch theory)
从表2和图6可知,改进的普氏平衡拱理论,克服了普氏平衡拱估值法的缺陷,合理地反映出了采空区跨度和安全顶板厚度之间的关系。同时,在侧压系数不变的情况下,采空区的跨度与采空区的高度对顶板的安全厚度影响很大,符合实际现场情况。
采空区上方有露天采矿作业的条件下,采动影响会对采空区上部岩体产生一定作用力,进而易使作用于拱脚处岩体的轴向压应力急剧增大,从而使该位置演变为顶板的最不利截面;此时,拱脚处会出现2种情况:一是在采空区帮部富集软弱岩体工况下,会导致采空区帮部发生片帮脱落,失去承载上部荷载的能力,此种工况下的采空区顶板的安全厚度需要依据变化后的扩展隐形平衡拱拱高来重新计算确定;二是在采空区帮部富集较坚硬岩体工况下,顶板上覆荷载增加,拱脚处暂未发生片帮冒落。此时,除计算扩展隐形平衡拱拱高外还需要计算该平衡拱的极限承载力、平衡拱上部岩层的跨中下侧最大拉应力及外部荷载在其采动影响下的重力。最终结合这几方面综合确定采空区顶板的安全厚度。
3.4 现场观测
以6022工作面为例,用钻孔彩色电视对采空区顶板裂缝产状及发育情况进行观测。该系统是把一自带光源的防水摄像探头放入地下钻孔中,对钻孔中地质体的各种特征及细微变化实时观测、监控和记录[24]。现场观测结果如图7与图8所示。

图8 不同时期钻孔窥视内部岩体裂隙发育情况Fig.8 Boreholes in different periods to peep at development of internal fissures
由图7可知,采空区顶板裂隙发育高度为128 m左右,且深部裂隙密集程度明显增多。1个月后的钻孔窥视结果显示,顶板内部平衡拱的发育高度为126 m,与初始高度相差不多,说明顶板内部平衡拱的发育高度变化不大。这与改进普氏平衡拱计算所得的顶板稳定性要大于传统普氏平衡拱的结论一致,说明改进普氏平衡拱的计算结论与实际吻合较好。

图7 钻孔窥视内部岩体裂隙(104~128 m)发育情况Fig.7 Drill holes to observe development of internal rock mass fractures(104-128 m)
4 结 论
1)传统普氏平衡拱理论在一定程度上客观反映了地下硐室顶板冒落的实际情况,但因为没有考虑水平构造应力对顶板平衡拱的影响,加之层状顶板采空区片帮形式的多样化和逐层冒落等特点,所以,传统普氏平衡拱应用于层状顶板采空区安全高度的计算中,在条件假设和分析推导方面仍然存在不足和缺陷。用未改进的传统普氏平衡拱理论计算表明当采空区的跨度越大,顶板最小安全厚度增幅较小,明显与实际工况相违背,以平衡拱拱高的2倍来估算采空区顶板的安全厚度存在缺陷,因此,需加以更正。
2)基于层状顶板变形规律研究,考虑采空区两帮稳定状态与平衡拱形态及拱高的关系,考虑采空区存在水平侧压力对拱的影响等,对传统普氏平衡拱理论进行改进,应用改进的普氏平衡拱理论计算结果合理地反映出了采空区跨度和安全顶板厚度之间的关系,在侧压系数不变的情况下,采空区的跨度与采空区的高度对顶板的安全厚度影响很大,理论结果与现场实际观测值相吻合。
3)使用彩色钻孔电视对选定区域的采空区顶板裂缝产状及发育情况进行观测,采空区顶板裂隙发育深度在128 m左右,1个月后裂隙发育深度为126 m左右,从顶板裂缝产状及发育情况进行观测分析得出改进普氏平衡拱计算所得的顶板稳定性要大于传统普氏平衡拱的结论一致,说明改进普氏平衡拱的计算结论与实际吻合较好,为露天煤矿工作面的正常推进提供参考依据。

