面向三维点云识别的体素网格降采样*

肖正涛，高 健，吴东庆，张揽宇

(1. 广东工业大学省部共建精密电子制造技术与装备国家重点实验室，广州 510006；2. 广东工贸职业技术学院机电工程学院， 广州 510510；3. 仲恺农业工程学院计算科学学院， 广州 510220)

0 引言

近年来，随着深度传感技术的发展与普及，三维点云的获取变得越来越容易。由于从三维点云中提取特征不易受比例、旋转和光照的影响，而且比从RGB图像中得到的信息更准确，因而深度传感技术得到了越来越多的关注，被广泛应用在自动化加工生产线、无人驾驶汽车等领域。

由于实际中得到的三维点云数据量庞大，且往往包含有一些噪声信息，在使用前通常要进行一些预处理[1]，包括去噪、降采样(downsampling[2])、点云数据结构化等，以提升点云的最终处理效果和效率。其中，降采样是点云预处理过程中一个非常关键的步骤，它不仅会影响点云的处理速度，还会影响最终的处理效果。对点云进行降采样处理简而言之就是对点云进行精简[3]，或者说就是减少点云中点的数量。点云降采样的方法有很多，如体素网格(voxel grid[4])法、系统采样(systematic sampling[5])、随机采样(random sampling[6])、最远点采样(farthest point sampling[7])等，这些不同的降采样方法通常有各自适合的使用场景。

体素网格法，也称体素栅格法，是一种常用的降采样方法。该方法先对三维点云建立轴向包围盒(axis-aligned bounding box, 简称AABB[8])，然后沿各个坐标轴方向将包围盒分成n等份，接着计算每一个体素中所有点的重心，最后将该重心作为该体素的采样值。体素网格法降采样的优点是计算效率高、采样点分布均匀，因而该方法得到广泛使用。

点对特征(point pair feature，简称PPF)三维物体识别算法由Drost B[9]在2010提出，是目前综合性能表现最佳的三维物体识别算法之一[10]，被广泛应用在机器人自主作业系统。Birdal T等[11]在OpenCV[12]中实现了PPF三维物体识别算法模块。在Birdal的源代码中，点云预处理阶段使用了体素网格降采样方法。笔者查看了Birdal在2014年9月提交的最初版本和在2020年1月提交的最新版本，Birdal在将体素的三维索引转换为一维索引时一直存在着错误。

本文针对OpenCV点对特征三维物体识别模块中体素网格降采样算法进行了深入研究，详细讲解了体素网格降采样方法的网格归属划分和体素的索引转换，分析了Birdal方法存在的问题，以及Birdal方法在降采样时可能会导致的后果，并给出了正确的体素三维索引到一维索引的转换表达式。通过实验比较，在极端情形，Birdal的方法不能正确降采样，而本文方法能正确完成降采样任务。

1 体素网格降采样方法

1.1 体素网格方法的实现

如图1a所示，对点云建立轴向包围盒，并沿各个坐标轴方向将包围盒分成n等份。在包围盒最上、最右和最后添加如图1b所示的虚拟体素，以接纳位于包围盒最上、最右和最后表面或棱线上的点。图1c将体素分组，不同的组用不同的颜色表示。图1d对包括假想体素在内的包围盒沿x、y、z三个坐标轴方向分别标记上索引，索引从0开始计数。

点云中任意点所在体素的三维索引(i,j,k)的计算式如下所示：

(1)

式中，i,j,k分别表示x、y、z轴方向从0开始的索引值，trunc表示截断取整(也称舍弃小数取整)，n表示包围盒沿x、y、z轴分成的份数(从1开始计数)，dx表示点到包围盒左侧面的距离，Lx表示包围盒沿x轴方向的边长，dy表示点到包围盒前表面的距离，Ly表示包围盒沿y轴方向的边长，dz表示点到包围盒下表面的距离，Lz表示包围盒沿z轴方向的边长。从式(1)可知，i,j,k的范围是0～n。

为了程序处理上的便利，我们需要将所有体素(包括虚拟体素)的三维索引转换为一维索引，如图1d所示。如果按照先x轴方向，然后y轴方向，最后z轴方向的顺序，转换式如下：

(c)将体素分组，不同的组 用不同的颜色表示 (d) 体素的三维索引到 一维索引的转换

idx=i*(n+1)(n+1)+j*(n+1)+k

(2)

式中，idx表示体素的一维索引，i,j,k∈[0,n]。这样，每一个三维索引(i,j,k)就唯一对应着一个一维索引idx。每一个一维索引idx也同样唯一对应着一个三维索引(i,j,k)，从式(2)可推知一维索引到三维索引的计算式如下：

(3)

式(2)和式(3)建立起了体素三维索引与体素一维索引之间的一一对应关系。

(a) 对点云建立轴向包围盒， 并对包围盒进行等分 (b) 假想在包围盒最上、最右 和最后添加虚拟的体素

式(1)对包围盒内和包围表面(包括棱线和顶点)上的点进行了归属划分，但不够直观，尤其是位于包围盒Top，Right和Back三个表面(包括相应的交线和顶点)上的点。将假想添加的体素分解，如图 2所示，每一组虚拟体素分别标记为Ψ1,…,Ψ7。标记出包围盒的Front，Top和Right面，与Front，Top和Right面对应的则是Back，Bottom和Left面。包围盒Top，Right和Back三个表面(包括相应的交线和交点)上的点的归属分别是：顶点D属于体素Ψ4，直线AD(除D点)属于体素Ψ5，直线BD(除D点)属于体素Ψ2，直线CD(除D点)属于体素Ψ6；Top面(除直线AD和直线BD)属于体素Ψ1，Right面(除直线AD和直线CD)属于体素Ψ7，Back面(除直线BD和直线CD)属于体素Ψ3。这种归属划分与式(1)是一致的。

图2 分解图效果

完成了体素网格的建立，空间点的划分和体素三维索引到一维索引的转换后，接着计算每一个体素中所有点的重心，最后将该重心作为该体素的采样值。

1.2 对Birdal算法的分析

在Birdal实现的点对特征三维物体识别模块的源代码中，Birdal使用如下的表达式将体素的三维索引转换为一维索引：

idx=i·n·n+j·n+k

(4)

其中，i,j,k的范围是0～n。

笔者认为式(4)是错误的，式(4)会直接导致不同的体素对应同一个一维索引。如索引为(1,0,0)的体素和索引为(0,n,0)的体素是不同的，但按照式(4)，它们对应的一维索引皆为n2，后果就是将不同体素中的点当作属于同一个体素的点。

更进一步探讨，式(4)会将哪些不同的体素对应为同一个体素呢?这个问题的数学描述就是：当i1=i2,j1=j2,k1=k2不同时成立时，求方程i1·n·n+j1·n+k1=i2·n·n+j2·n+k2在i1,j1,k1,i2,j2,k2∈[0,n]且n≥2时的非负整数解。这是一个求解整系数线性方程组的整数解问题[13]，特别之处是此时方程组中的方程只有1个，未知数有6个。为了便于分析，我们将这个方程变换成如下形式：

n2(i1-i2)+n(j1-j2)+(k1-k2)=0

(5)

(6)

由于i1,j1,k1,i2,j2,k2∈[0,n]，因而i1-i2,j1-j2,k1-k2∈[-n,n]，根据式(6)，可得到下面这组线性不等式[14]：

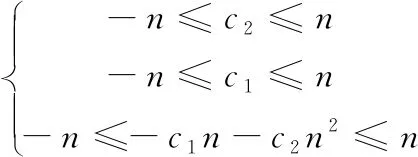
(7)

不等式组(7)的解有6组，如下：

(8)

此时，式(6)即可转化为下面6组方程组：

(9)

分析式(9)中的6组方程组，每组方程组等号右边皆有一项不是n就是-n，也就是说，对于每组方程组，i1-i2,j1-j2,k1-k2中必有一项等于n或-n。由于i1,j1,k1,i2,j2,k2∈[0,n]，可知每组方程组中的i1,i2或j1,j2或k1,k2必有一组只会是0和n。

在三维索引(i,j,k)中，当其中一个索引分量为0或n时，此三维索引对应的体素一定位于包围盒表面，如图1d所示。我们已经知道，Birdal用来转换体素三维索引到一维索引的计算式(4)会导致不同的体素可能对应同一个一维索引。现在我们更确切地知道，式(4)会将位于包围盒表面的不同体素对应为同一个一维索引。因而，Birdal算法对位于包围盒表面上的点有可能不能正确降采样。

2 实验与分析

本文的实验点云数据有两个：①图3a中人工制作的长方体点云，该点云的所有点皆位于一个长方体的6个表面，且长方体的各个表面与相应的坐标面皆平行，这个特殊点云的轴向包围盒为该长方体自身；②图3c中的加机工零件点云，该点云是用CREAFORM HandySCAN 700手持式三维激光扫描仪扫描图3b所示的一堆机加工零件获得，该点云只有非常有限的几个点位于轴向包围盒表面。图3a和图3c中的绿色线框为各自点云的轴向包围盒。本文实验以OpenCV和PCL (Point Cloud Library)为计算平台，计算机配置是Intel 酷睿I5-7200U，12 GB内存。本文分别使用Birdal算法和本文方法对三维点云进行降采样，并从降采样的直观效果、计算时间、降采样前后变化等多个方面进行了比较和分析。

长方体点云和机加工零件点云包含的点数、点云轴向包围盒的尺寸大小以及体素网格降采样时包围盒每边将要分成的等分数如表 1所示。

表1 实验点云的一些数据

用Birdal方法和本文方法分别对图3a所示的长方体点云进行降采样处理，包围盒沿各个坐标轴方向分成的份数皆为n=5。Birdal方法得到的降采样结果如图4a所示，除了x方向包围盒左右两个表面有点外，其余所有点皆落在包围盒内部，也就是说，包围盒其余4个表面上皆没有点。本文方法得到的降采样结果如图4b所示，包围盒6个表面皆有点，只在靠左、靠前和靠下的位置有一些采样点位于包围盒靠近表面的内部。直观上看，两种方法对长方体点云进行降采样得到的结果差异非常大。

(a) 长方体点云 (b) 机加工零件 (c) 机加工零件对应的点云

用Birdal方法和本文方法分别对图3c所示的机加工零件点云进行降采样处理，包围盒沿各个坐标轴方向分成的份数皆为n=40。Birdal方法得到的降采样结果如图4c所示，本文方法得到的降采样结果如图4d所示。直观上看，两种方法对机加工零件点云进行降采样得到的结果无明显差异。

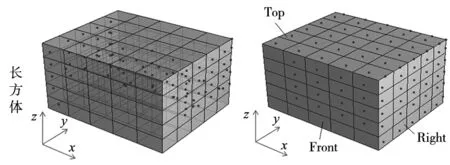
(a) Birdal方法，包围盒半透明显示 (b) 本文方法

表2展示了Birdal方法和本文方法对长方体点云和机加工零件点云降采样的一些数据。无论是对长方体点云，还是对机加工零件点云，Birdal方法和本文方法在计算时间上没有显著差异。对长方体点云来说，无论是降采样后的点数量，还是降采样后的点云到原始点云的距离，Birdal方法和本文方法皆有非常显著的差异；从降采样后的点云到原始点云的距离来看，Birdal方法得到的值皆比本文方法得到的值要大，说明Birdal方法得到的点云与原始点云的差异比本文方法要大。对机加工零件点云来说，无论是降采样后的点数量，还是降采样后的点云到原始点云的距离，Birdal方法和本文方法得到的结果是一样的。

表2 降采样结果

在计算降采样后的点云到原始点云的距离时，我们可以得到降采样后的点云中每一点与原始点云的最小距离，将这些最小距离值绘成频数分布直方图，如图5所示。在图5中，横轴表示降采样后的点云中的点到原始点云的最小距离，横轴被分成若干个间隔，以方便进行频数统计。纵轴表示降采样后的点云中到原始点云的距离在某个范围内的点有多少。为了便于直观对比分析，图5a和图5b的横轴和纵轴的刻度范围、距离间隔皆一致，图5c和图5d也是如此。对长方体点云而言，从图5a和图5b可知，Birdal方法得到的点云中有相当一部分点与原始点云的距离偏大，而本文方法得到的点云总体上与原始点云的距离更小，也即本文方法得到点云更接近原始点云。图5c和图5d的频数分布直方图基本相同，表明两种方法得到点云也基本相同。

(a) Birdal’s (b) Ours

表3展示了不同方法得到的降采样点云之间的距离值，用于比较两个点云之间的差异情况。通常情况下，若A，B两个点云不同，那么从A点云到B点云的距离，与从B点云到A点云的距离往往是不同的。若A到B的距离越小，则表明A与B越相似。若A到B的距离为0，则表明A是B的子集，若同时B到A的距离也为0，则表明B也是A的子集，此时可知A与B相同。表3中，对降采样后的长方体点云而言，除了最小值这一项为0外，其余皆不为0。最小值这一项为0，表明Birdal方法得到的点云与本文方法得到的点云有重合的部分；其余项不为0，表明Birdal方法得到的点云与本文方法得到的点云在整体上是不相同的。表3中，对降采样后的机加工零件点云而言，Birdal方法所得的点云到本文方法所得的点云的距离值皆为0，且本文方法所得的点云到Birdal方法所得的点云的距离值也皆为0，这表明两种方法得到的降采样后的机加工零件点云是一样的。

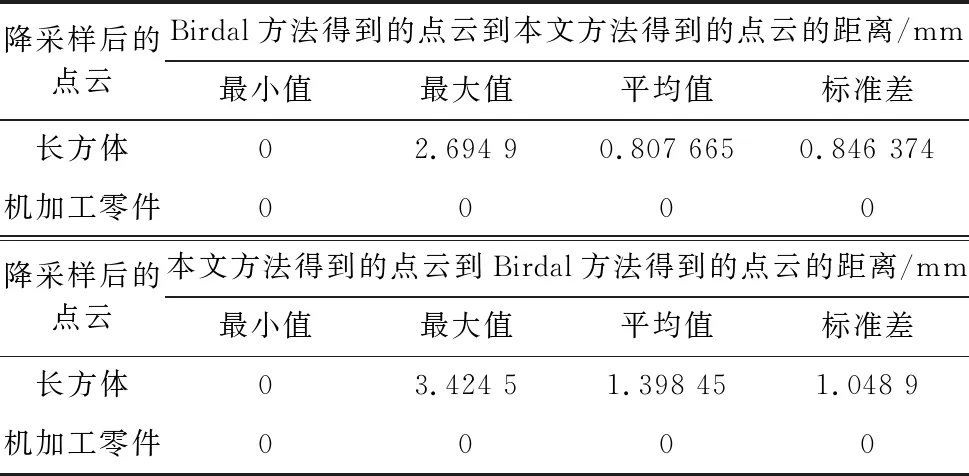
表3 降采样后的点云比较

从上面的结果和分析我们可知：Birdal方法对特殊的长方体点云不能正确降采样，得到的结果与原始点云有较大的差异，Birdal方法对加工零件点云可以正确降采样；本文方法无论是对特殊的长方体点云还是机加工零件点云皆能正确降采样。

对Birdal方法而言，若点云包围盒表面有点，且这些点所在的体素索引满足方程(5)，则点云将不能被正确降采样。当这两个条件不能同时满足，使用Birdal方法就可以对点云进行正确降采样。这也就是为何机加工零件点云存在着几个位于包围盒表面上的点，而Birdal方法仍可以对该点云正确降采样的原因所在。

3 结论

针对OpenCV中体素网格降采样算法存在的错误，本文提出了一种体素网格降采样算法，该算法的关键是对点云中的每一个点正确划分网格归属，并将网格的三维索引转换为与之一一对应的一维索引。理论分析和实验结果均表明，当点云中的点位于包围盒表面时，OpenCV中的体素网格降采样算法不能对点云进行正确降采样，而本文提出的体素网格降采样方法则可以正确有效地对各种情形的点云进行降采样。实验结果同时表明，两种降采样方法在计算时间上无明显差异。