非均匀热流密度下多孔介质内氨反应特性研究

阮景昕,邓泽宏,胡 甜,王跃社,3

(1.西安交通大学动力工程多相流国家重点实验室，西安 710049;2.中国核动力研究设计院核反应堆系统设计技术国家重点实验室， 成都 610213;3.中国电建太阳能热发电工程研究中心，西安 710065)

0 前 言

伴随着中国能源转型步伐的加快，利用可再生能源如太阳能、风能、地热能代替传统能源是实现“碳达峰，碳中和”目标的重要途径之一。其中，太阳能因其储量丰富性、环境友好性将成为能源变革中主要的可替代能源[1-2]。目前利用的太阳能发电技术主要有2种：光伏发电和光热发电。太阳能热发电技术通过聚焦的方式将低能流的太阳能转变为高能流的热能，加热工作介质然后推动汽机发电。由于太阳能在时间和空间上分布具有不连续性和不稳定性，为保证电能的安全稳定输出，在太阳能热发电站中嵌入储能系统是关键一环。根据能量利用的形式，目前储能系统有三大类：显热储能、潜热储能以及热化学储能。其中，热化学储能方式因具有储能密度高、储能体积小、可常温存储、热损失小等优势而成为研究热点。相比于其他热化学储能方式，氨基热化学储能又有如下优点：氨来源丰富，成本低廉；氨可逆反应无副反应产物；氨反应器结构简单；合成氨技术很成熟，因此它是一种很有前途的储能方式。

基于氨的能量存储方法包括氨合成和分解的热化学循环过程。氨分解是吸热反应，氨合成过程是放热反应，这些过程被循环利用以存储和释放能量。目前合成氨技术已经很成熟，而对系统吸热侧的氨分解反应的研究尚处于初级阶段。合成氨的高效催化剂并不适合氨分解[3]，因此需要单独对氨分解反应动力学机理进行特定的研究。赵朝晖等人[4]以La-CoMoNx/CNTs为催化剂，通过确定本征动力学参数，建立了氨分解制氢的反应动力学模型，发现其反应机理符合Temkin-Pyzhev机理。

国内对氨基热化学储能系统研究很少，尤其是针对储能系统中的氨反应器研究更是屈指可数。华南理工大学龙新峰等人[5-6]通过建立氨化学反应模型，加入反应动力学模型，数值模拟分析了氨基蓄热系统的效率、热性能。对氨基热化学储能研究主要集中在澳大利亚和美国。澳大利亚国立大学和美国科罗拉多大学主要针对氨基储能的工程设计、吸热器研制以及高压下镍基催化剂性能的研究[7-11]，建立了氨反应器的雏形并沿着管长方向建立了一维的氨分解反应模型用于拟合反应的活化能和指前因子以及分析氨反应管的性能。此后Lovegrove等人搭建了1个电加热的氨反应系统[12-13]，该系统包含了氨分解和合成氨反应，在实验过程中通过流量控制器来设定氨入口流量值，通过测量壁面上的温度以及反应物温度和给定的电功率来计算热损。同时他还建立了二维的准均匀的固定床催化剂反应器计算模型，分析了操作温度、压力以及入口流量对氨分解率的影响情况。Siddiq[14]针对合成氨反应器建立了一维稳态的准均匀流动模型，他发现在最佳运行模式中，氨的产量相比参考模式可以提高15%，在最佳模式中要求入口温度达到900 K，高于一般工业合成氨的700 K左右。此外还有一些学者对整个系统做了一些瞬态模拟，如Bran-Anleu等人[15]建立了一维合成氨子系统的流动换热及反应模型，研究了入口温度和流速对系统响应的影响，发现当流速增大时，反应器出口达到稳定的时间缩短了，同时发现如果入口速度过低，出口温度达不到650 ℃。Calro等人[16]采用Temkin-Pyzhev方程建立了小型反应器内氨分解反应模型，模拟了三维下的氨反应，发现在有反应选择膜的情况下，在550 ℃左右，氨基本完全分解，比无膜情况下转化率提高18%。类似的现象也在Valentina等人[17]的文献中出现，即在常规填充反应器中引入Pd基膜，获得了比在足够高的温度下的热力学平衡转化率更高的氨分解转化率。在研究氨基储能系统的性能时，另一个核心问题是研究多孔介质内氨分解的化学反应。Ni采用局部热平衡方法建立了一个二维甲烷重整反应用于研究反应器结构和各种操作参数对产氢含量的影响[18]。Wang等人[19]在研究多孔介质容积式反应器内甲烷蒸汽重组性能时，采用局部非热平衡模型和P1近似辐射模型研究稳态条件下多孔介质内固体和气体温度分布。

目前研究氨基热化学储能中的氨分解反应或者合成氨反应，所建立的数值模型大多为一维、二维，模型中也没有涉及到管内气体流动以及组分传输与反应之间的影响机制。本文构建一个多孔介质内氨催化分解反应的三维模型，从本质上去揭示氨分解反应与气体流动及组分传输的关系，总结氨反应能质传递和转化的一般规律，通过对模型的离散求解，针对催化剂颗粒直径以及孔隙率分布，提出实际的反应管优选参数及设计方法，为提升氨反应管性能提供支撑。

1 氨反应管模型建立

1.1 物理模型

本实验研究的氨反应管内氨分解过程如图1所示，太阳辐射能聚焦在氨反应管上，反应管中的氨气通过与管壁和催化剂多孔介质进行换热升温，并在催化剂表面活性作用下发生高温催化分解反应产生氢气和氮气。塔式太阳能热发电系统中氨反应器表面的太阳能流密度分布是不均匀的。因此，导致其温度分布也是不均匀的。氨反应器为总长L，半径R0的圆管，均匀尺寸的直径为dp的NiO-Al2O3催化剂颗粒被包装在反应器内。随着气体在反应管内的浓度扩散，该氨分解反应过程是一个多孔介质内高温化学反应耦合气体传热传质过程。特别的是由于反应管束竖直、平行且紧密地排布在吸热器表面，因此，管壁面只有一半面向太阳辐射，另一半面紧贴吸热器并可被认为是绝热表面。

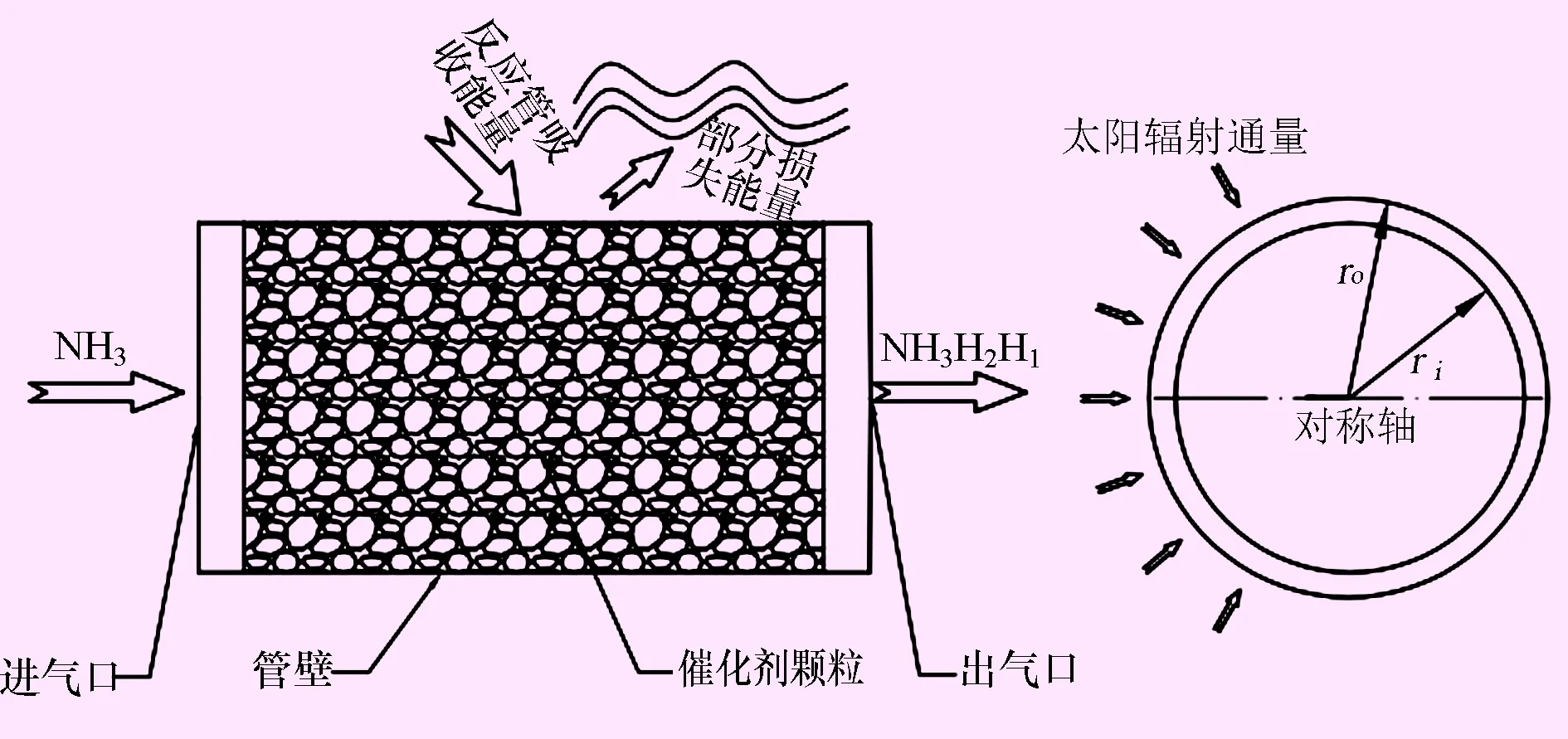
图1 反应管内氨分解过程示意图

1.2 数学模型

本文采用考虑轴向、径向和周向的三维模型模拟单根反应管内氨催化分解反应的特性。接下来对本研究中使用的单管催化反应器作以下假设：

(1) 由于反应管长径比很大，因此，径向上的扩散作用可忽略不计，只考虑轴向和周向上的热扩散和质量扩散。

(2) 由于多孔介质中氨气接近层流流动状态，因此，忽略径向和周向上的流动，只考虑管轴向上的流动。

(3) 由于管周长相对管长可以忽略，因此，假定太阳能流密度沿着管周向方向均匀布置，只在管长方向有一定分布。

(4) 由于氨分解的反应温度不是特别高(500～600 ℃)，根据陈等人[20]的研究可以发现不考虑管内辐射偏差小于4.5%，因此，在本模型中忽略颗粒间及颗粒与气体间的辐射换热。

由于反应管内气体与多孔介质间存在一定的温差,本模型采用局部非热平衡模型进行建模。基于以上假设在稳态条件下可得流体侧能量守恒方程：

-MNH3R′ΔH+hsfAsf(Ts-Tf)

(1)

式中:ρm为混合气体密度，kg·m-3；um为混合气体表观速度，m·s-1；Cp,m为混合气体比热容， J·kg-1·K-1；ε为反应管孔隙率；λf为流体导热系数，W·m-1·K-1；R′为氨分解速率，kmol·m-3·s-1；ΔH为化学反应焓变，J·kg-1；hsf为固体与流体间换热系数，W·m-2·K-1；Asf为比表面积，m-1。

对于固体侧可得：

-hsfAsf(Ts-Tf)

(2)

式中:λs为固体导热系数，W·m-1·K-1。

对于气体组分氨，根据质量守恒可得：

(3)

式中:f为氨气质量分数；Df为气体扩散系数，m2·s-1；MNH3为氨摩尔质量，kg·kmol-1。

整个化学反应及流动过程的压降可以采用Ergun Equation[21]来近似计算：

(4)

实际中壁面的边界条件应为太阳能流密度分布，但由于实验只能控制壁面的温度，而温度与太阳能流密度一般成正向关系。因此，本文将温度分布等价于太阳能流密度分布。太阳能流密度空间分布近似高斯分布，因此，本文也假定温度沿着管长方向呈高斯分布：

(5)

式中:z为沿轴线方向的距离，m；σ为温度分布的有效偏差系数，用于表征温度分布均匀程度。

由于管壁有一定的厚度，管壁内壁面和外壁面间的导热根据圆管壁傅里叶导热定律可得：

(6)

在上述能量和质量守恒方程中，对于氨分解速率，本文采用经典的Temkin-Pyzhev公式，它适用于反应接近平衡状态，其表达式为：

(7)

式中：k0为反应指前因子， mol·m-2·s-1；Eα为反应活化能，此处的值为1.92 105 J·mol-1；k为气体常数，值为8.314 J·mol-1·K-1；kp为化学反应平衡常数；dp为催化剂颗粒直径，m。

当反应远离平衡时假定反应速率只与氨的分压有关[22]，给出了氨在远离平衡状态下的表达式为：

(8)

能量守恒方程中的固体与流体之间的换热系数以及比表面积根据Wakao经典公式[23]可得：

(9)

流体侧反应管入口边界条件为气体入口温度和流量，固体侧由于在边界处不考虑轴向的扩散情况因此沿轴向方向导热为零：

m(r,θ,z=0)=minδ(r,θ,z=0)=1

(10)

根据Amiri对加热壁面的研究[24]，固体壁面和液体壁面温度局部相等，热流根据各自的有效导热系数决定，因此，内管壁边界条件为：

(11)

本模型假定外管壁涂有选择性吸收涂层，外管壁吸收的能量为：

qin=ξqs-qloss

(12)

式中:qin为单位面积壁面吸收的热量，W·m-2；ξ为吸收率；qs为单位面积壁面投入的热量，W·m-2；qloss为壁面与大空间的热损失，W·m-2；hw,a为壁面与外界空气之间的换热系数，W·m-2·K-1；x为实际物体发射率(黑度)；σ0为黑体辐射常数， 5.67×10-8W·m-2·K-4。

其中壁面与外界空气间的换热系数求解过程如下：

(13)

式中:L为特征长度，m；v为空气运动粘度，m2·s-1；μ为空气动力粘度，Pa·s-1；λa为空气导热系数，W·m-1·K-1。

本文中取壁面温度为550 ℃，空气温度为25 ℃，因此定性温度为287.5 ℃，此时μ=2.952×10-5Pa·s，v=4.774×10-5m2·s-1，Cp=1.043×102J·kg-1·K-1，λa=4.309×10-2W·m-1·K-1。

2 数值模型验证

本文对数值模型进行了网格无关性验证，分别在横截面上选取5×5、10×10、20×20、30×30、40×40、50×50共6组网格，管长方向上选取10、20、100、200、500、1000个网格进行模拟，模拟的氨分解率和管中心出口温度结果分别如图2、3所示。

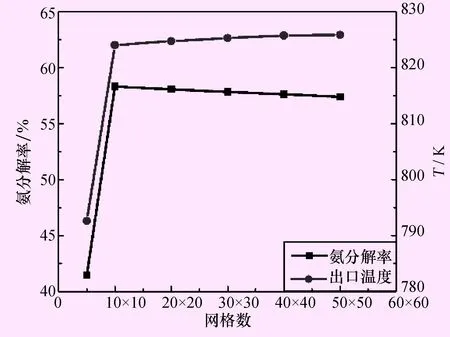
图2 氨分解率与横截面上网格数关系图

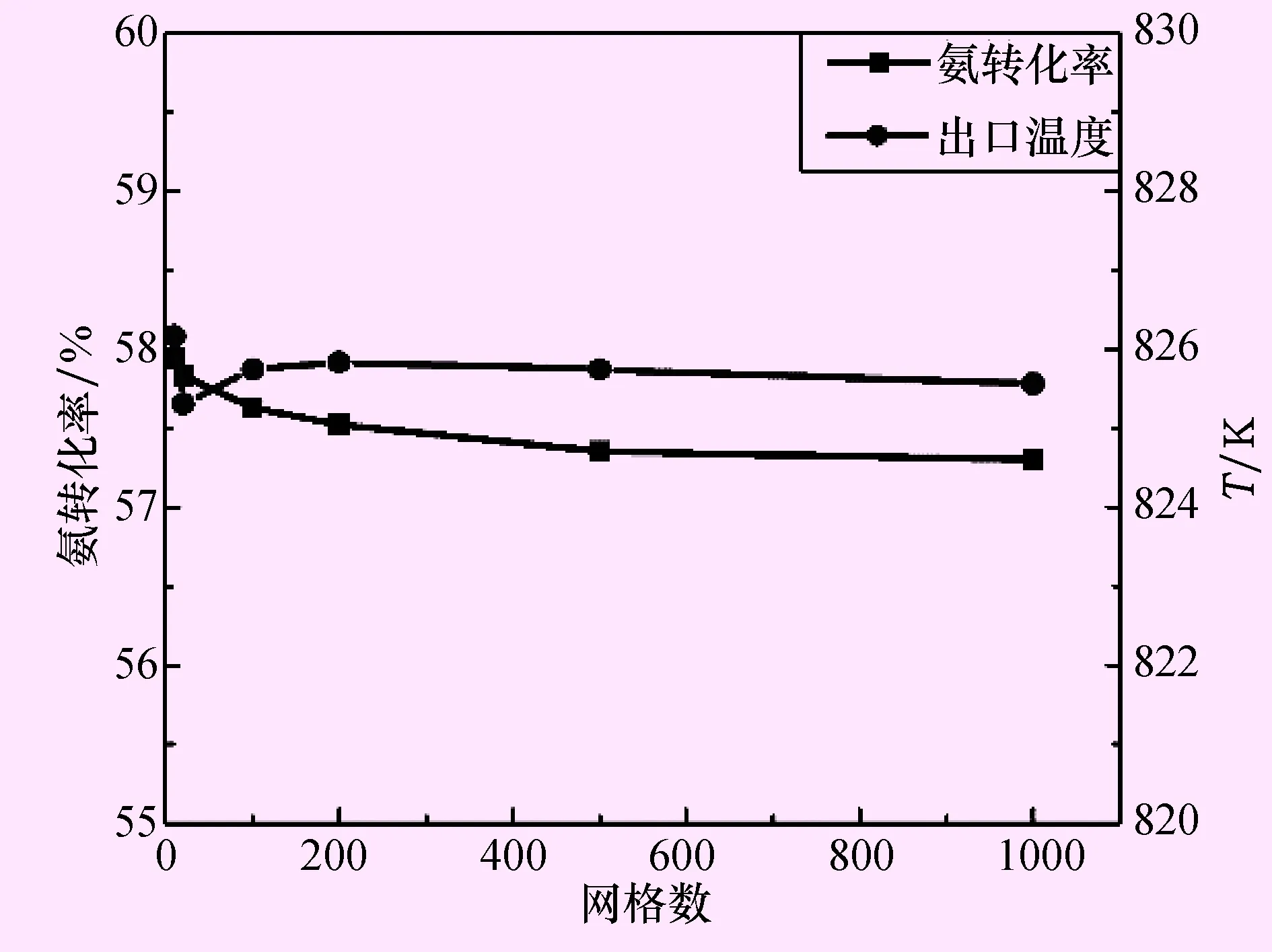
图3 氨分解率与长度方向网格数关系图

可以发现当横截面上网格为30×30，管长方向为500以上时，结果变化很小，基本可认为此时网格的变小对模拟结果没有大的影响。因此，本模型最终选取网格数为30×30×500共计450 000网格。

本研究还实际搭建了1个氨分解吸热实验平台，设定实验条件为：常压，流量0.5～4 L·min-1，温度400～500 ℃，入口温度50 ℃。然后将氨分解反应的实验测量值与模拟计算值进行比较，对比结果如图4所示。可以看到在低流速下模拟值与实验值差距较大，但是在相对高流速下二者的值吻合较好。实际上在低流速下管壁温度由于容易受到外部环境影响而非完全均匀分布，但模拟过程中又设定管壁温度为恒定值。因此，在低流速下模拟结果会有较大误差。

图4 氨分解反应的模拟值与实验值对比图

经验证在高流速下本模型可以较好地模拟氨催化反应的过程，接下来研究氨反应过程中能质传递、转化的一般规律以及催化剂颗粒对氨分解率的影响。将模拟条件设定为：颗粒直径0.5～2 mm，孔隙率0.2～0.8，入口流量17g·s-1，入口温度200 ℃，出口压力2 MPa，热流分布偏差系数2.5。采用控制变量法研究催化剂颗粒大小及分布对氨反应的影响规律，模型原始参数设置如下：颗粒直径1 mm，孔隙率0.5。

3 讨论与结果

3.1 氨分解热-化学能转换一般规律

氨反应过程牵涉到流动传热、导热、组分传输等过程。在流动方面，如果不考虑质量流量的变化，假定反应速度远大于流动速度，则流动过程主要涉及到固液之间的对流传热；在导热方面主要涉及到壁面与固体骨架的导热以及骨架之间的导热，与骨架的有效导热系数有关；组分输运则主要与气体有效扩散系数有关。表1给出了固体和流体换热系数、有效导热系数、有效扩散系数对氨反应的影响。

表1 固体和流体换热系数、有效导热系数、有效扩散系数对氨反应的影响表

从表1中可以看出有效导热系数和有效扩散系数的改变会对氨反应过程产生一定影响，而固流换热系数的改变几乎没有影响到氨反应过程。一般来说固体和流体之间的换热系数比较大，所以气体和固体之间温差不大，因此改变固体和流体换热系数不会对氨反应产生大的影响，这与表1所示结果一致。

接下来研究导热系数与管内热量传递间的关系，高、低导热系数下外壁面和管中心气体温度差着管长方向变化情况如图5所示。在高导热系数条件下，壁面温度和管中心的温度差很小。此时如果壁面温度也比较小，那么散热损失就少，因此热效率升高的同时氨转化率也会升高。

从表1还可以看出当有效扩散系数增大时会导致管壁峰值温度降低，这可能是由组分在不同区域的扩散引起的。接下来本文分别模拟了高扩散率和低扩散率时的管内横截面上氨质量分数径向分布情况。不同扩散系数条件下的氨质量分数和温度沿管径方向变化如图6所示，在高扩散系数条件下，氨气在管内分布更为均匀，同时温度也更为均匀。同时可以看到在近壁面区域，高扩散系数下的气体温度要低于低扩散系数下的气体温度，这就可以降低管壁的峰值温度。并且扩散作用使得绝热低温区域的氨气能扩散到高温管壁附近，因此在整个反应过程中，气体的扩散作用有可能利于氨的分解反应。

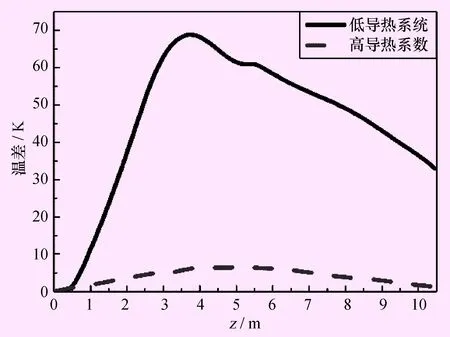
图5 高、低导热系数下外壁面和管中心气体温度差沿着管长方向变化情况图

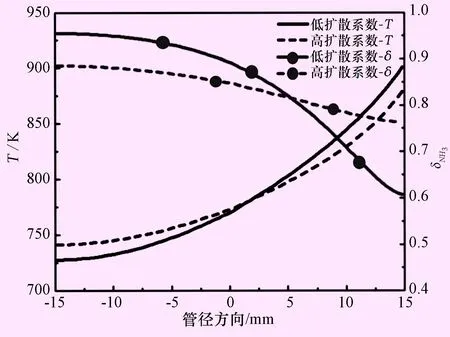
图6 不同扩散系数条件下的氨质量分数和温度沿管径方向变化图

3.2 孔隙率与颗粒直径对氨分解率的影响

本文研究了氨反应管性能与孔隙率和颗粒直径之间关系。模拟了催化剂颗粒直径在0.5、1、2 mm下的氨分解反应，不同孔隙率和颗粒直径条件下反应管性能对比如图7所示。

通过分析结果可知，氨分解率随着孔隙率的增大先缓慢减小然后再迅速下降;随着孔隙率的增大，热效率降低的同时管壁峰值温度上升;在相同孔隙率下颗粒的粒径越小，氨分解率和热效率越高，并且管壁峰值温度和温度不均匀性也下降了。这说明小的颗粒直径和孔隙率减小有利于反应管内氨的反应，但这需要反应管内填充更多的催化剂材料并且使整个反应管的沿程阻力增大，制造和运行成本相应上升。

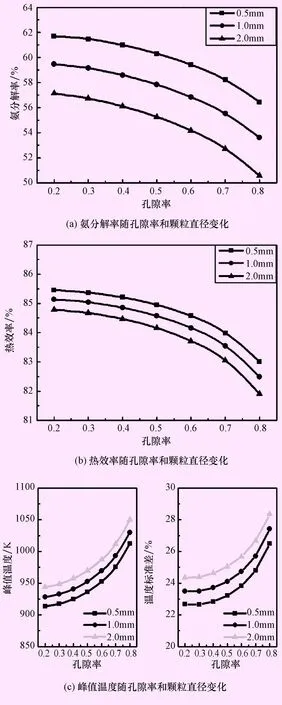
图7 不同孔隙率和颗粒直径条件下反应管性能对比图

3.3 径向孔隙率分布对氨分解率的影响

氨分解催化剂的成本在整个氨反应管中占比较高。本文将进一步探究在使用相同重量的催化剂时，径向孔隙率如何分布才能优化氨反应管性能，使氨分解率上升，同时管壁峰值温度下降。本文模拟了孔隙率径向线性分布且平均孔隙率为一定值的情况，例如孔隙率沿管径方向的分布为0.3～0.7，即表示在管中心位置孔隙率为0.3，在管壁位置孔隙率为0.7。由于径向上的孔隙率有变化，因此在模拟中径向界面上的有效扩散系数在同一个界面的两侧的值不一致，模拟时取界面相邻的2个单元体的有效扩散系数的平均值作为该界面上的有效扩散系数。径向孔隙率分布对氨反应的影响结果如表2所示，孔隙率沿管中心到管壁方向减小时，氨的转化率会提高，孔隙率减小的斜率越大，氨分解率越高，同时热效率有一定的上升且管壁峰值温度也降低。

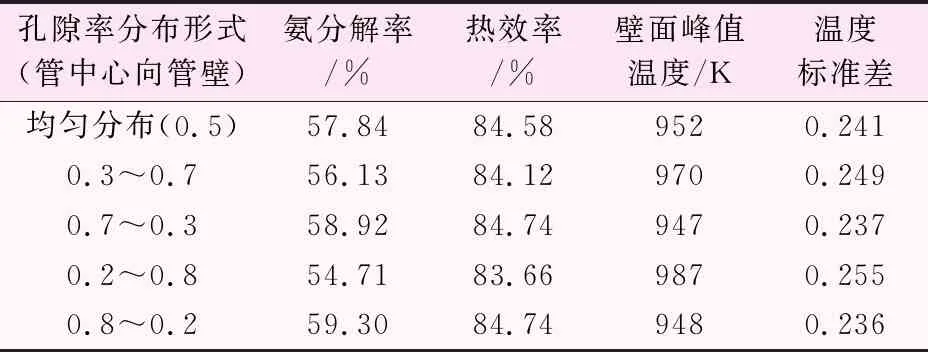
表2 不同孔隙率沿径向分布的结果对比表

如图8所示为2种孔隙率径向分布下的氨反应管对称面上气体温度分布云图，可以看到孔隙率分布为0.2～0.8时气体的峰值温度更高，但气体温度在径向方向上下降得更快，导致了壁面附近温度更高而管中心附近温度更低。在反应管前端，孔隙率分布为0.8～0.2的气体温度升高速度明显更快。这是由于近壁面处的低孔隙率会使固体骨架的有效导热系数升高，加强了固体与壁面间的导热，在相同的辐射能量条件下反应管热损较小，气体吸收的能量更多升温更快。

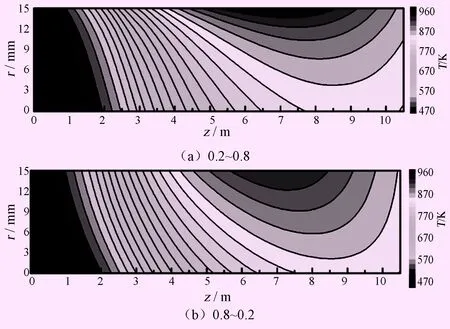
图8 2种孔隙率分布下反应管对称面上气体温度云图

如图9所示为氨反应管对称面上气体反应速率云图，从中可以看出气体高反应速率的面积在孔隙率分布为08～0.2时更大。当孔隙率分布为0.2～0.8时，管壁处的高孔隙率会在一定程度上会减弱氨分解反应速率，其整体上的化学反应速率也会低于孔隙率分布为0.8～0.2的情况。以上结果均表明可以采用孔隙率径向线性减小分布的方式来提高氨反应管性能。

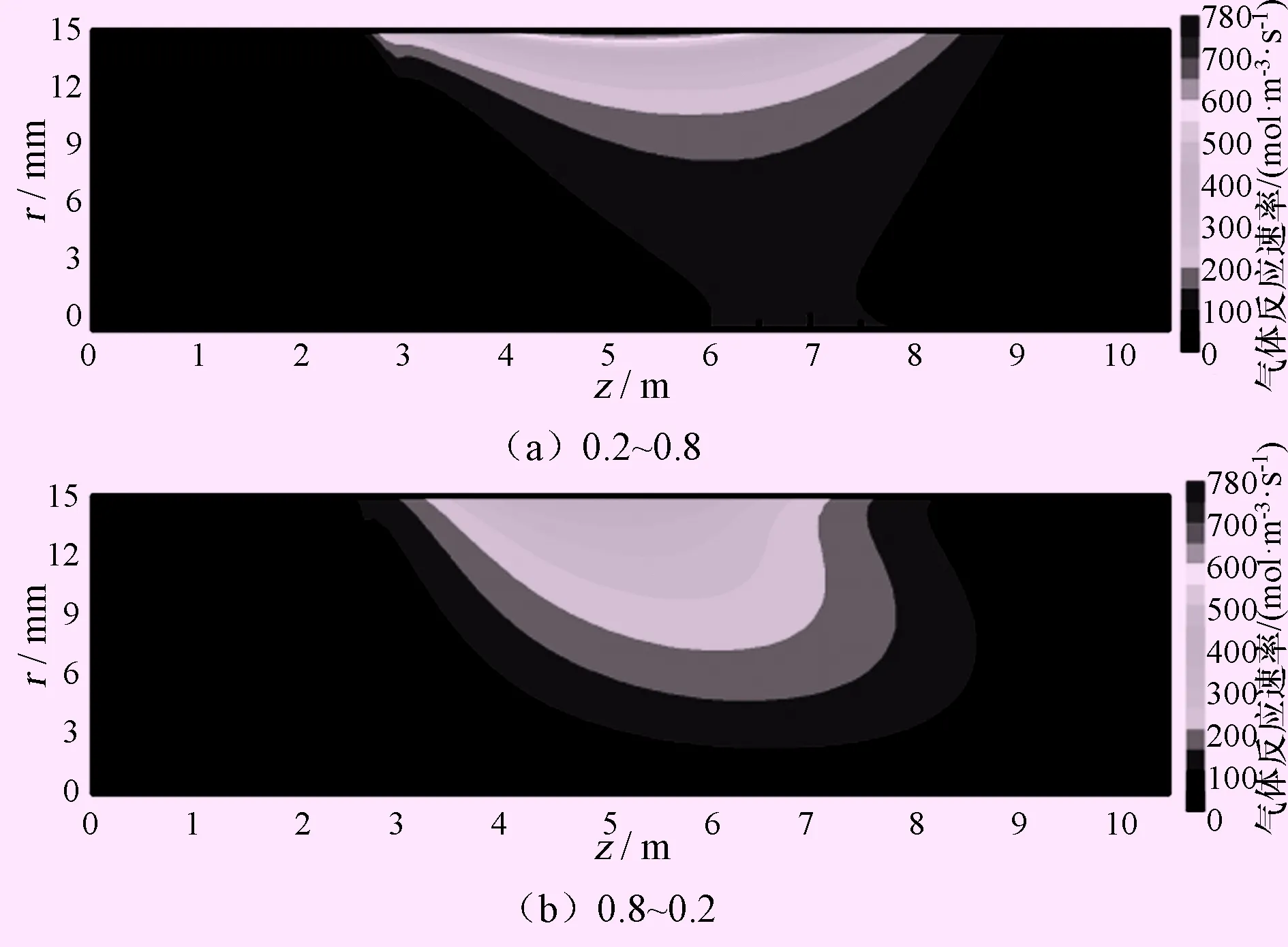
图9 2种孔隙率分布下反应管对称面上气体反应速率云图

4 结 论

本文基于氨催化分解的动力学模型，建立了1个三维多孔介质内氨分解反应与流动及组分传输耦合的能质传递及转换模型，揭示了氨分解反应特性，进一步研究了反应管内催化剂颗粒直径和孔隙率分布对氨反应特性影响。主要结论如下：

(1) 一般来说，固体和流体的换热系数越大，固体热量更容易导入流体中，氨分解率越高，由于本文模型中换热系数已经较大，所以改变换热系数大小对氨分解反应影响不大。

(2) 有效导热系数对氨分解反应影响较大，有效导热系数越大，壁面和固体骨架间的传热能力就越强，在同样的传导热量下壁面和固体的温差越小，散热损失减小，热效率升高的同时氨转化率也有所提升。

(3) 有效扩散系数主要影响不同位置处生成物的扩散，使得反应管内的气体和温度分布得更加均匀，低温区域的氨扩散至高温区域，提升氨转化率的同时降低了管壁面温度。

(4) 通过对催化剂颗粒直径和孔隙率的研究，分别分析对比了颗粒直径、孔隙率的变化对氨分解反应的影响。结果表明，催化剂颗粒直径越小，孔隙率越小；氨的分解率越大，同时壁面峰值温度越低。这是由于小颗粒直径和小孔隙率不仅导致有效导热系数增大，还在相同温度条件下提高了化学反应速率。

(5) 针对孔隙率分布，发现采用径向孔隙率线性减小的分布方式可以在降低壁面峰值温度的同时又不降低氨分解率。

为了优化单根氨反应管性能，可以将催化剂颗粒直径定为0.5 mm，其孔隙率为径向分布0.8～0.2的线性分布方式。