基于切换系统的小推力轨迹优化协态初始化方法

武 迪，程 林，王 伟，李俊峰

（1. 清华大学 航天航空学院，北京 100084；2. 北京航空航天大学 宇航学院，北京 100191）

引 言

以电推进为代表的小推力推进系统近年来受到了广泛的关注，相较于传统化学推进，电推进具有更高的推进效率，即更能节省燃料[1]。自“深空1号”（Deep Space 1）探测器成功验证电推进技术后，“黎明号”（Dawn）、“隼鸟号”（Hayabusa）和正在进行的“贝皮科伦布”探测器（BepiColombo）等深空任务均采用了电推进发动机。而在近地任务中，波音公司的Boeing 902SP和中国的“实践十七”“实践二十”将电推进技术应用于地球同步轨道的入轨和轨道保持任务[2]。因此，电推进技术由于其出色的推进效率，在未来航天任务设计中将逐渐获得更普遍的应用。

在轨道设计方面，由于电推进所产生的推力较小，需要长时间的开机工作才能产生足够的速度增量，以电推进驱动的航天器小推力最优轨迹将和脉冲推进的最优轨迹产生显著的差别。圆锥曲线拼接[1]、基于形状的标称轨道方法[3]等相对解析的设计方法难以实现对小推力最优轨迹的准确近似。而对于一般的深空探测轨道设计，在连续推力作用下的轨道无法采用类似解析的方法得到最优解，而是采用较为耗时的数值优化的方法（主要为直接法和间接法）[4]。

对于探测任务尤其是多目标任务的全局规划问题[5-6]，需要快速且准确地确定小推力轨迹的燃料消耗、转移时间等参数。因此，实现对小推力轨迹的快速优化具有重要意义。

目前，主要的数值优化方法分为直接法和间接法[7]。

直接法将小推力优化问题进行离散，转化为非线性规划问题求解，通常需要较多的离散点以提高解的精度和最优性[8]。相较于直接法，间接法利用极大值原理构建两点边值问题求解，能够保证最优性的一阶必要条件[9]。但是这些数值方法均需要提供初值进行优化，直接法需要提供离散点的状态和控制初值，比较容易利用设计经验或标称轨道方法得到，而且直接法的收敛域相对较大，其求解对初值敏感性较弱[8]，因此其计算性能主要取决于离散点数。间接法需要提供协态的初值，相较于具有实际物理意义较容易猜测的状态，协态并无明确的物理意义，其取值范围也难以确定，因此较难提供初值[1]。同伦方法[9]将小推力燃料最优问题通过同伦参数联系转换为求解相对较容易的能量最优问题求解，提高了初值猜测成功的概率。协态归一化方法[10]通过引入归一化参数将协态的猜测范围限制在高维单位球面上，提供了初值猜测的范围，进一步提高了初值猜测的效率。基于标称轨道的协态初值估计方法[1]能够提供能量最优问题的初值猜测，但是其猜测的成功率依赖于标称轨道的设计，对于较复杂的任务，标称轨道与最优轨迹偏离较大，协态估计的效果较差。因此针对小推力间接法轨迹优化，解析的保证收敛的协态初值能够显著降低求解失败的概率，以提高小推力轨迹优化的效率。

本研究提出了一种解析的协态初始化方法，引入切换系统，将小推力燃料最优问题同一个具有解析初值的轨迹优化问题相联系，通过迭代方法求解得到小推力燃料最优轨迹。本文首先将小推力优化模型嵌入到更为广义的切换系统模型中，给出了切换系统的构建形式，并设计了相应的切换函数，从而将小推力优化问题转化为更简单优化模型的优化问题；其次，给出了具有解析协态初值的简单系统优化模型，能够通过切换系统与小推力优化模型相联系，进一步给出了计算迭代算法，并通过数值仿真验证了该方法相较于传统同伦方法，具有更高的求解效率。

1 切换系统及切换函数

针对常见的小推力轨迹优化问题，本节首先给出了一般指标形式下的小推力轨迹优化模型，其中动力学模型也采用了一般的矩阵形式描述。在此优化模型的基础上，进一步介绍了切换系统的概念，从而将小推力优化模型嵌入进更广义的切换系统优化模型中，同时给出了切换函数设计。

1.1 小推力轨迹优化模型

一般而言，考虑如下小推力轨迹优化模型，优化指标为

其中：指标J1通常取为总的燃料消耗[9]、能量消耗[1]、飞行时间[8]或混合指标；表示状态矢量，通常由航天器的位置、速度（或轨道要素）和质量组成，即表示控制量，通常包括控制量幅值及其方向。动力学方程为

此优化模型可以转化为两点边值问题并采用间接法求解。相比于直接法，间接法能够保证最优的一阶必要条件，因此一旦求解成功即可得到局部最优的轨道。但另一方面，在间接法的求解过程中需要人为提供无物理意义的协态初值猜测作为求解的初始化，而且间接法的收敛域也较直接法更小，难以对估计不准的协态初值实现成功求解。因此，优化时的初值猜测情况会显著影响间接法的求解成功率和效率，当前主要采用随机猜测的方式多次猜测求解，猜测成功率较低且求解效率较慢。

基于协态初值估计的方法，本文将小推力优化模型嵌入进切换系统中，同时设计切换系统形式使其具有解析的协态初值，避免了初值猜测困难。以此解析协态初值作为初始化，通过切换函数迭代实现了小推力最优轨迹的快速求解。

1.2 切换系统设计

基于小推力轨迹优化模型，引入如下一般形式的切换系统[11]优化模型。优化指标为

动力学方程为

一般而言，传统的从能量最优问题同伦求解燃料最优问题的算法，将同伦参数添加到优化指标中，而动力学方程保持不变。此时，首先求解能量最优问题的协态初值，然后逐渐改变同伦参数值，以得到的协态初值作为猜测值，求解对应同伦参数下的优化问题，最终得到燃料最优解。

与传统方法不同，本文的优化模型将同伦参数引入到两个系统之间的切换函数中，系统1的优化指标为动力学方程的右函数为。系统2的优化指标为动力学方程的右函数为采用同样的同伦过程即可得到燃料最优解。在本文中，系统1设计为小推力燃料最优轨迹优化模型，系统2及其解析协态初值的设计将在下一节中详细给出，切换函数设计为

根据极大值原理，系统的最优控制使哈密顿函数

2 燃料最优轨迹优化

基于标称轨道线性化的方法，本节首先给出了系统2的模型，并进一步给出了确定小推力燃料最优轨迹的求解算法。

2.1 解析协态初值

系统2考虑如下线性优化模型。优化指标为

另外，对于标称轨道的选取，在本文中仅考虑的简单线性的标称轨道，具体形式为

由于系统2设计即为简单线性的优化模型，此种标称轨道能够进一步简化解析解求解的难度，快速给出解析协态初值。本文的数值仿真证明此标称轨道能够处理较为复杂的燃料最优问题。

根据极大值原理可得最优控制律为

因此，得到了一个线性时变的动力学微分方程，此方程中系数仅和标称轨道以及当前时刻有关，而和状态、协态无关。此方程的解可以解析得到

对于深空探测中的交会问题，通常考虑如下末端条件

由于此系统中质量为常数，质量协态的初值并不影响此系统的解，因此在计算中将质量协态的初值设为0，即将式（16）代入式（15），其它协态初值的解析表达式为

2.2 燃料最优轨迹优化算法

对于燃料最优问题，系统1的指标取为燃料消耗，系统2的指标中取值和系统1保持一致，即

将式（18）代入切换系统的表达式，可得切换系统的优化指标为

3）以上一步收敛的协态初值作为打靶量的初值进行打靶；

4）若打靶收敛，则转到步骤2继续求解过程，若打靶不收敛，则以更小的步长重新转到步骤3计算；

5）当同伦参数为0时，输出收敛的小推力燃料最优轨迹的结果。

3 数值仿真

本节仿真试验了自地球出发前往不同目标[1]的深空探测轨迹，以验证方法的有效性。在仿真中，采用了ODE45积分器，其相对误差和绝对误差设置为打靶算法采用Minpack-1，其参数设置参考相关文献[10]。为加快积分并降低数值敏感性，归一化参数设置为长度单位1 AU（天文单位），时间单位1年，质量单位归一化为航天器初始质量。此时，太阳的引力常数为所有算例均以C++语言编写（Microsoft Visual Studio 2012编译），并在台式机使用单核运行（Intel Core i7-7 700 CPU，主频3.6 GHz，内存8.0 GB）。

算例任务参数如表1所示，由于本文采用春分点轨道根数描述，因此各个算例的航天器轨道圈数同时给定。相应时刻的地球和目标的位置速度可根据JPL系统查询得到。

表1 数值仿真任务参数表Table 1 Parameters for the numerical simulation missions

3.1 计算效率对比

本文方法的计算效率和传统能量到燃料最优同伦方法的计算效率进行了对比。这两种方法均应用了前文所述的迭代过程。由于能量最优求解需要进行随机猜测初值，因此其每个算例进行了1 000次随机猜测并记录收敛个数。而本文方法采用线性的标称轨道，且由于具有解析初值仅进行单次计算即可。相应的计算收敛率、所需的迭代步数和得到单个解的平均计算时间如表2所示。本文方法对3个算例均能够实现100%收敛，而传统同伦方法的收敛率分别为86.7%、83.6%和39.3%，尤其是对第3个算例，传统方法收敛率较低，计算效率差别较大。

表2 该方法与传统同伦方法计算效率对比Table 2 Table1 Comparisons of proposed method with the traditional homotopic method

3.2 燃料最优解

对每个任务，迭代过程中的控制曲线如图1所示。对于地球至金星的任务，飞行时间为700 d，燃料最优控制包含6个关机段和5个开机段，总的开机时长为275.1 d，消耗燃料210.45 kg。对于地球至“坦普尔1号”（Tempel 1）任务，燃料最优控制包含2个关机段和3个开机段，最短的关机段为初始的弧段，时长0.63 d。任务中总开机时间为197.7 d，消耗燃料348.36 kg。地球至小行星3 671（Dionysus）的任务总时长为3 534 d，燃料最优控制包含7个关机段和6个开机段，总计开机时间1 361.5 d，总计燃料消耗1 279.93 kg。3个任务场景的燃料最优轨迹如图2所示，地球至金星任务为2圈近圆轨迹，轨道倾角改变较小，求解相对较为容易，因此本文方法和传统同伦方法均具有较高的求解效率。Tempel 1的轨道为椭圆轨道，因此，此任务的控制曲线较为复杂，而计算所需的迭代步数较多。Dionysus的轨道为倾角较大的椭圆轨道，本文方法求解此问题所需时间仅为传统方法的1/5。

图1 各任务迭代过程的推力曲线图Fig. 1 History of the thrust magnitude of different missions

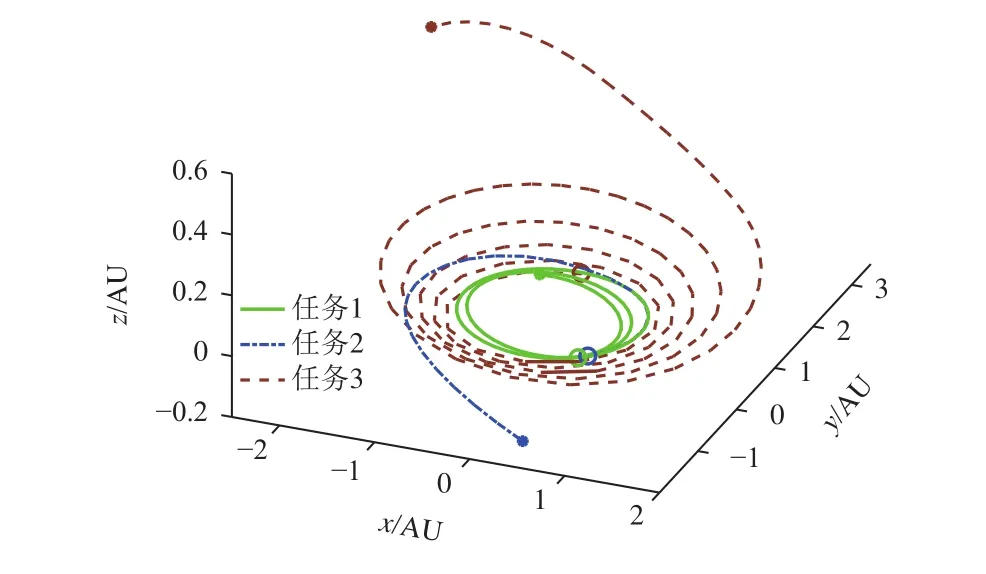
图2 各任务场景的燃料最优轨迹图Fig. 2 Fuel-optimal trajectories of different missions

4 结 论

该研究提出了基于切换系统的解析初始化方法，将小推力燃料最优轨迹优化问题同具有解析协态初值的线性优化问题联系起来，能够解析初始化，并提高间接法小推力燃料最优轨迹的求解效率。仿真表明：本方法和从能量最优同伦至燃料最优轨迹的方法所需的迭代步数基本相同，而其协态初值能够解析得到，因而具有更高的求解效率。