深空高速撞击的变系数末制导律设计方法

郑惠欣，彭玉明，王 伟，谢 攀，陆 希，李海洋，陈 晓

（1. 上海卫星工程研究所, 上海 201109；2. 上海市深空探测技术重点实验室, 上海 201109）

引 言

近地小行星（Near-Earth Asteroid，NEA）为轨道与地球相交或相近的小行星[1]，现一般认为与地球间的相对距离小于0.05 AU且直径大于140 m的近地小行星会对地球构成巨大威胁[2]，这类小行星被称为“潜在危险小行星”（Potentially Hazardous Asteroid，PHA），撞击地球后将会造成不可挽回的区域或全球规模危害，具体表现形式主要有：地震、海啸、冲击波、热辐射等。

近百年来发生的较严重的小行星撞击事故包括：通古斯大爆炸（1908年），一颗直径50 m的小行星发生空爆，损毁的西伯利亚森林面积约2 000 km2[3]；车里雅宾斯克爆炸事件（2013年），一颗直径约20 m的小行星在俄罗斯上空解体爆炸，由于事故发生在人类活动区，破坏性极大，造成了约1 500人受伤，3 000栋房屋受损[4]。小行星撞击地球后会对人类的生存、生活构成极大威胁，如何防止小行星撞击地球事故的发生是防御任务的重点[5]。

目前，改变近地小行星轨道的防御手段主要可分为3种：施加长期作用力、动能撞击及核爆炸[6]。其中，高速动能撞击是现阶段应用最多、效果较好的一种方式，世界各国共设计了近20种面向不同目标天体的撞击器，如美国的“深度撞击”（Deep Impact）任务）、俄罗斯的“火星96”（Mars 96）和日本的“月神A”（Luna A）等[7]。

深空高速撞击任务的研究难点包括撞击器与目标的相对速度大、撞击精度要求苛刻、携带燃料受限等，为了使撞击器能够顺利完成任务，精确制导技术是决定任务成败的关键因素。目前国内外针对撞击末制导律的设计方法可分为两大类：基于预测制导的制导方法和基于比例导引的制导方法[8]。

美国发射的Deep Impact撞击器采用的是预测制导技术[9]，其基本思想是结合观测信息，通过对撞击器及目标的动力学方程进行轨道积分，实现对撞击器的定轨，并估算当前撞击点。根据当前撞击点与期望撞击点间的差值设计制导律，解算得到需用的速度增量及加速度指令。预测制导技术的优点是实施简单，可直接得到所需的机动速度，缺点是需要预先给定撞击器机动时刻[10]。Deep Impact任务在地面站进行了大量蒙特卡罗仿真，预先给出了3次机动时间，机动时刻无法根据实际任务需求变化，带来撞击精度和燃料消耗间的矛盾：机动时刻越靠前，改变撞击器轨道所需的燃料消耗越少；随着撞击器与目标相对距离的减小，导航精度的增加会提高撞击精度，但改变轨道所需的速度增量会变大。

国内外学者后基于比例导引（Proportional Navigation Guidance law，PNG）针对撞击末段设计了制导律，可无需地面事先确定机动时刻。纯比例制导律（Pure Proportional Navigation Guidance law， PPNG）生成的加速度指令为连续变量，无法应用于依靠脉冲发动机完成轨道机动的深空撞击器。学者们对此进行了一些改进研究，包括：文献[11]提出了一种针对卫星拦截任务的比例导引法，在发射惯性坐标系中利用目标和拦截器的实时绝对状态参数构造相对运动参数，计算推力矢量方向以达到抑制视线转率的目的；在此基础上，文献[10]设计了一种视线制导律，引入B平面点位误差椭圆以描述预测撞击点的置信度，并将其转换为对脉冲发动机开关机曲线的设计，可在节省燃料的同时提高撞击精度；文献[12]比较了PPNG、增广比例导引（Augmented Proportional Navigation Guidance law，APNG）和预测制导3种算法在执行同一撞击任务时的撞击精度、燃料消耗等。

上述研究中，目标的加速度（目标和撞击器所受到的太阳引力差及目标对撞击器的引力作用）对撞击效果的影响不是重点研究内容，在初始相对距离较远或撞击器与目标相对速度很大的情况下，目标的实际加速度会导致终端误差增大，影响撞击效果；同时，所设计的比例制导算法中全过程的比例系数为一固定常值，系数取值不同会使得生成的加速度指令大小变化，进而影响所需的速度增量及燃料消耗。

基于对潜在危险小行星撞击防御的任务需求进行分析，本文提出了一种基于增广比例导引的深空高速撞击变系数末制导律，在撞击器与目标小行星初始距离较远、相对速度较大的场景下，考虑目标运动加速度，在保证抑制探测器与目标视线旋转的同时能根据目标的运动情况产生相对应的加速度指令；考虑撞击器在距离目标越远的情况下进行机动消耗燃料越少，基于增广比例导引，将比例系数设计为相对距离的归一化函数，控制视线旋转速率，在减少终端制导误差的前提下使点火时间更少、更靠前，节省燃料消耗；设计脉冲点火策略，将连续的加速度指令转化为撞击器可直接使用的脉冲加速度指令，无需事先给定撞击器机动时刻。通过数值仿真，验证了所提出的算法能够保证撞击精度，在相对速度较大情况下使探测器顺利完成撞击任务；且对比了比例制导系数为定值的算法，证明了本文所提出的变系数制导方法能够更节省燃料消耗。同时，为更贴近实际应用场景，在仿真中考虑了多种误差对算法制导精度的影响，通过蒙特卡洛结果证明算法在具有误差情况下制导精度较高，具有工程应用价值。

1 目标及撞击器动力学模型

本文以威胁度较大的近地小行星Bennu（编号101955）为预设目标，推导设计基于增广比例导引的深空高速撞击变系数末制导律。

首先，在日心惯性坐标系下建立目标及撞击器的动力学模型，目标及撞击器的几何关系如图1所示。

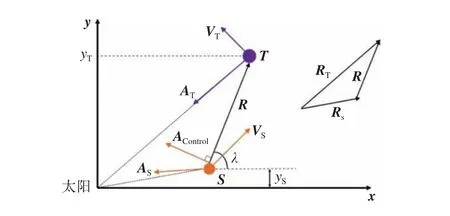
图1 目标及撞击器几何关系示意图Fig. 1 Geometric relationship between target and impactor

图1中坐标系原点为太阳中心，由于目标及撞击器的大小与轨道半径相比很小，因此将目标与撞击器均视为质点。目标受太阳引力作用运动，撞击器受到的被动外力包括太阳引力和目标小行星引力，主动外力为有控发动机产生的推力，两者的运动方程可表示为

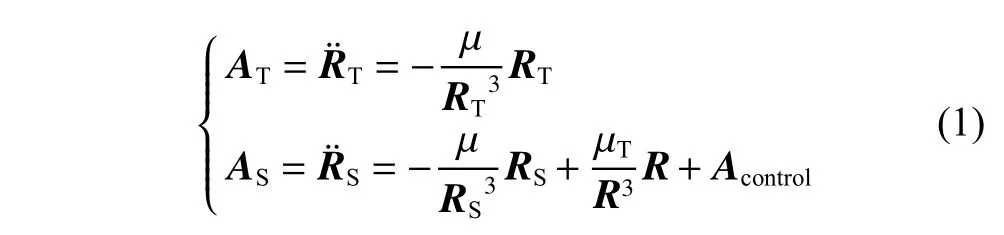
目标及撞击器的相对速度及太阳系中的绝对速度大小可由对应的位置矢量大小微分得到

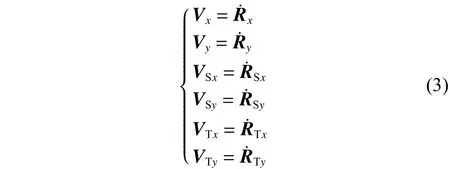
其中： Vx、Vy为撞击器相对于目标的相对速度在x、y 轴上的分量； Rx、Ry为撞击器与目标的相对位置矢量在 x 、y 轴上的分量；VSx、VSy、VTx、VTy分别为撞击器和目标在太阳系中的绝对速度分量；RSx、RSy、RTx、RTy分别为撞击器和目标相对太阳的位置矢量RS、RT在x 、 y轴上的分量。

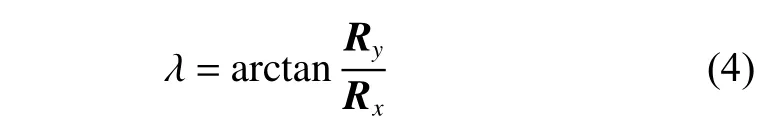
对式（4）进行微分，可得视线角随时间的变化率

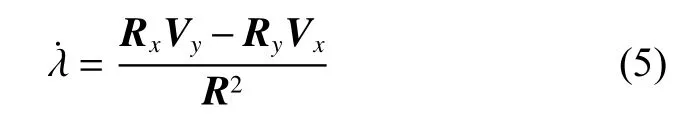
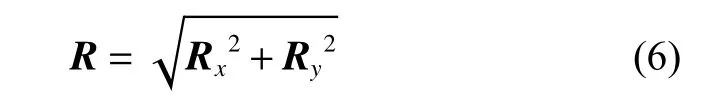
2 制导律设计

2.1 深空高速撞击变系数末制导律设计

比例导引算法是一种被广泛应用于寻的导弹制导领域的方法[13]，算法的基本思想为通过设计合理的法向加速度指令，使导弹速度矢量的旋转角速度与弹目视线角的旋转角速度成比例，从而达到抑制视线角速度的目的。

纯比例导引律在目标速度为常值且无加速度的前提下较为有效，针对非匀速运动目标，可利用APNG产生额外的加速度指令[14]，使轨迹更平缓光滑，且满足撞击精度要求。下面针对深空高速撞击任务，参照文献[12]推导变系数增广比例末制导律。

按照比例导引律的基本思想，设计加速度指令使撞击器的速度矢量旋转与视线矢量旋转成正比，可得

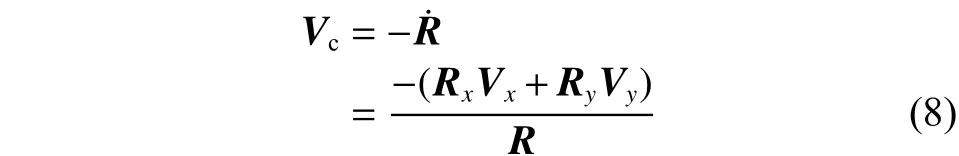
为满足撞击要求，在终端撞击时刻，目标与撞击器的相对距离大小应为0，即终端零控脱靶量（Zero Effort Miss，ZEM）应为零（零控脱靶量的定义为在不对撞击器施加控制指令的情况下，撞击器与目标沿各自运动轨迹的最短相对距离大小）。

在考虑目标加速度的情况下，零控脱靶量可表示为

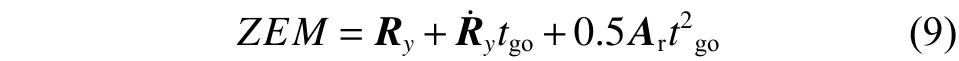
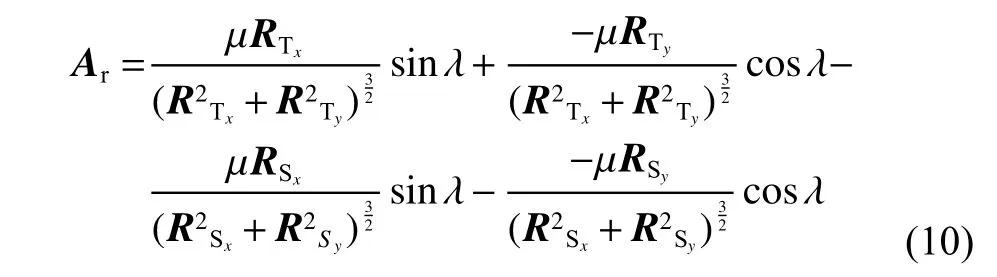
其中：前两项为太阳引力作用于目标的加速度分量，后两项为引力作用于探测器的加速度分量。目前工程中较常用的获得目标加速度的方法为利用地面测定轨技术及星历推算确定目标的轨道及位置速度信息，进而推算目标加速度[1,10,15]，本文中的目标加速度均为理论值。

增广比例导引律的基本思想是在加速度指令中考虑由太阳引力引起的零控脱靶量，推导得控制量指令为

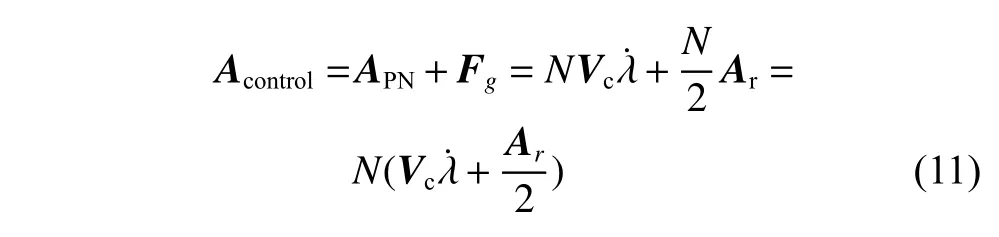
因此在利用基于比例导引的制导律求解具体问题时，怎样合理地根据任务需要设定比例系数的大小是一个比例导引律应用的开放问题。

相比传统的寻的导弹制导任务，小行星高速撞击防御的任务特点包括相对距离变化大、初始相对速度大，携带燃料有限、飞行时间长等，若在全过程应用不变的常值比例系数，可能会导致额外的燃料消耗或无法满足撞击精度要求。本文考虑将比例系数设计为相对距离的归一化幂函数，表达式为

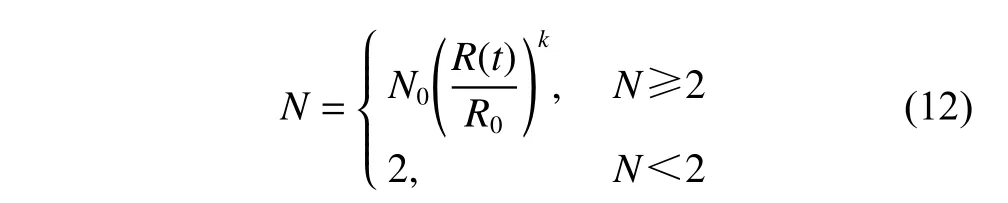
所设计的比例系数函数在不同系数取值下的变化如图2和图3所示。

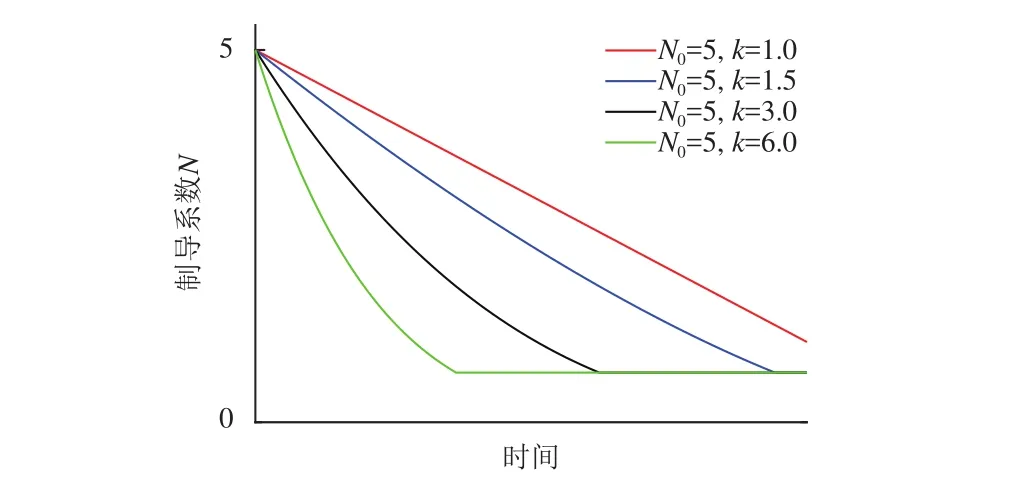
图2 比例系数N随k变化示意图Fig. 2 Augmented Proportional Navigation coefficient varies under different k values

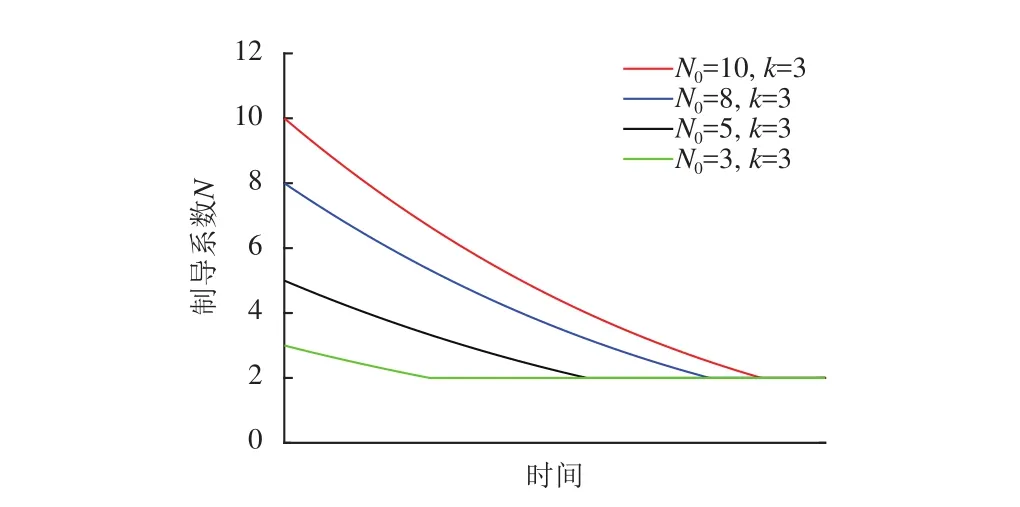
图3 比例系数N随N0变化示意图Fig. 3 Augmented Proportional Navigation coefficient varies under different N0 values

从图2中可以看出，所设计的归一化幂函数随相对距离变化单调递增（随时间变化单调递减），即在撞击任务的前期使用较大的比例系数进行控制指令的生成，使得撞击器的速度尽快“追上”相对视线角。

撞击器在相对目标距离较远时进行机动更节省燃料，利用本文所提出的变系数制导方法，撞击器距离目标越近，取值越小，所计算的加速度指令也越小。通过合理设计归一化幂函数，能够在满足撞击精度的前提下节省燃料消耗，后续研究方向考虑最优参数设计。

2.2 脉冲点火策略

利用2.1节提出的深空高速撞击变系数末制导律生成的控制量指令为连续函数，深空撞击器携带的脉冲发动机无法提供连续变化的推力。可利用施密特触发器（Schmitt trigger）逻辑[13]来应用制导指令，具体的操作流程如图4所示。

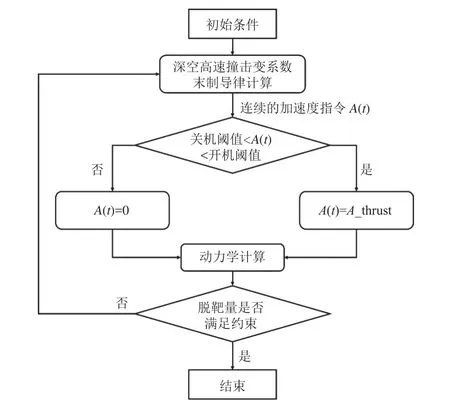
图4 脉冲点火策略逻辑Fig. 4 Flowchart of Schmitt trigger algorithm

1）输入初始状态量：目标/撞击器在日心坐标系下的绝对/相对初始位置、速度大小，并计算得视线方向角及其变化率的初始值

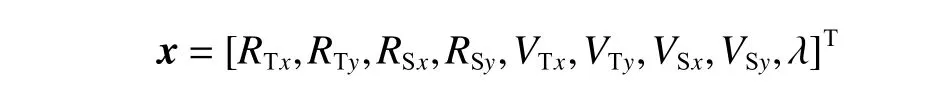
2）以当前时刻的目标位置作为期望的撞击点，利用2.1节提出的深空高速撞击变系数末制导律，根据式（12）由当前相对距离解算出的制导系数，代入式（11）计算得连续的加速度指令。

3）根据文献[11]中的施密特触发器逻辑，判断当前时刻连续的加速度指令是否处于开机区间内，若是则令加速度指令等于脉冲发动机的工作加速度值，若不在开机区间内，则当前时刻脉冲发动机不工作。

4）将第3）步中得到的实际加速度指令代入探测器动力学，得到探测器当前位置。

5）判断当前时刻探测器与目标间的位置关系是否满足撞击精度要求，若不满足则将当前时刻状态量值作为下一时刻的初始值，从步骤1）开始重复计算；若满足约束则算法结束。

3 数学仿真与分析

3.1 目标小行星Bennu

根据近地天体动态网站（NEODys）[16]对近地小行星危害程度（Risk List）的排序信息，小行星Bennu的危害程度被标记为“特殊”（Special），且危害程度位居前三，其近地点距离地球的距离仅40万km。

美国国家航空航天局（National Aeronautics and Space Administration，NASA）于2016年9月发射了OSIRIS-Rex（Origins Spectral Interpretation Resource Identification Security Regolith explorer）小行星探测器，目标是小行星Bennu。科学家预计，在2 175—2199年，小行星Bennu有2 700分之一的概率与地球相撞，对地球存在极大的威胁。小行星的轨道信息如表1所示。

表1 小行星Bennu轨道信息Table 1 Orbit information of Asteroid Bennu

因此本文将以小行星Bennu作为防御撞击对象进行仿真分析，以验证算法在深空高速撞击领域的有效性。

3.2 数值仿真结果

为了验证本文所提出的深空高速撞击变系数末制导律算法的性能，选取高危近地小行星Bennu为撞击目标，在MATLAB语言环境下采用4阶Runge-Kutta数值积分器[17]进行解算。具体的仿真参数如表2所示。

表2 仿真参数值Table 2 Simulation parameter value

仿真初始时刻小行星位于其近地点，为了更好地展示算法的有效性，设置初始的相对速度为初始相对距离为9.363 59×105km。

假设撞击器在最后10 min时关闭推进器进行无控飞行。选取制导系数 N0=8，k=2，在测量无误差的情况下应用本文提出的基于增广比例导引的变系数末制导算法生成加速度指令，得到的目标及撞击器的运动轨迹如图5所示，相对距离变化如图6所示。

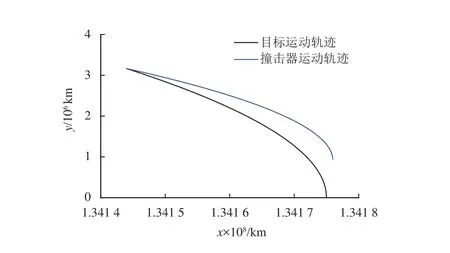
图5 目标及撞击器运动轨迹图Fig. 5 Trajectories of target and impactor

图6 撞击器与目标相对距离变化曲线Fig. 6 Relative distance history between impactor and target

从图6可看出，撞击器在生成的制导指令控制下能够成功完成撞击任务，撞击器和目标间的相对距离由初始时刻的 9 .363 59×105km 减小为3 .53 m，撞击精度较高。

本节还对比了采用本文所提出的变系数末制导算法和采用常系数末制导算法的结果，包括加速度指令、脉冲发动机工作情况、全过程所需速度增量及终端制导误差值。

表3对比了3种情况下的脉冲发动机工作情况、完成撞击任务所需的速度增量及撞击精度，可以看出，使用本文所提出的算法合理设计比例系数函数，能够在同等撞击精度下有效减少发动机点火次数及完成撞击任务所需的速度增量，减少能量消耗。

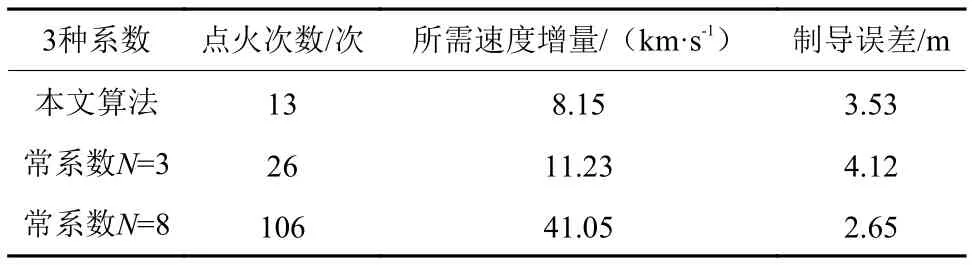
表3 变系数算法与常系数算法的任务结果对比Table 3 Task results comparison under different N value (the proposed method, N=3, N=8)

在3种不同的比例系数取值下的加速度指令曲线如图7（本文所设计变系数算法）、图8（常值N=3）、图9（常值N=8）所示。

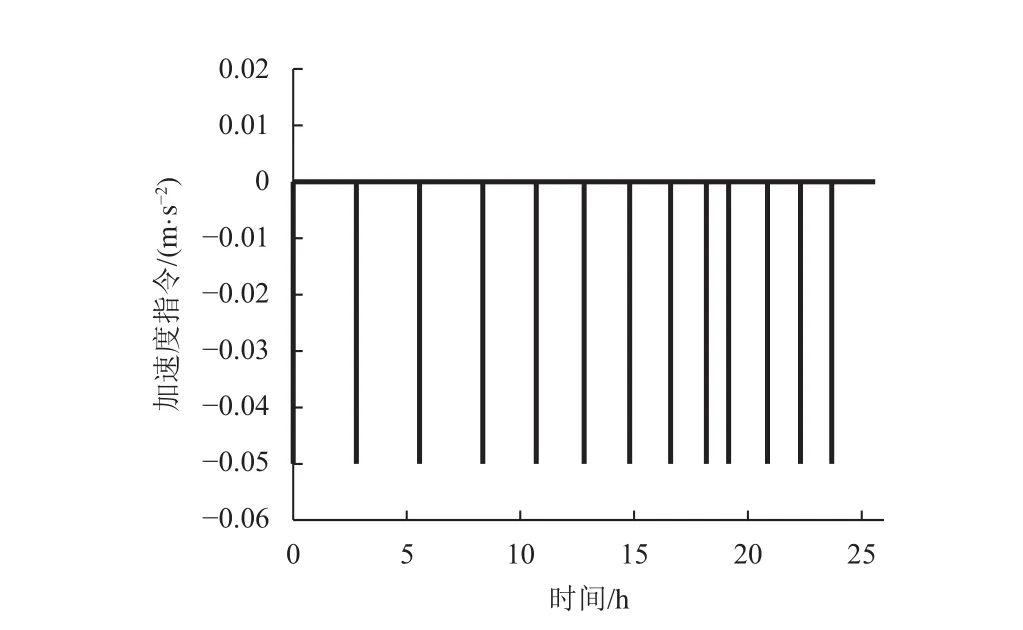
图7 采用本文算法的加速度曲线Fig. 7 The acceleration history generated by the proposed algorithm

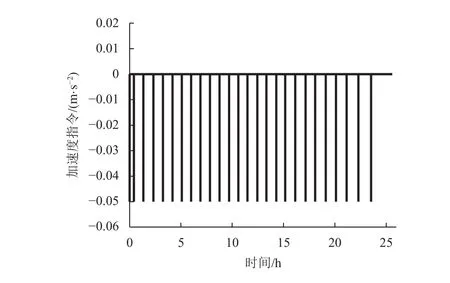
图8 采用常值系数N=3的加速度曲线Fig. 8 The acceleration history generated under a constant parameter N=3

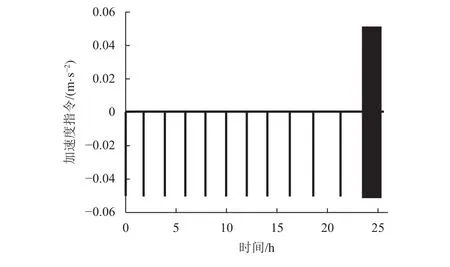
图9 采用常值系数N=8的加速度曲线Fig. 9 The acceleration history generated under a constant parameter N=8

从3种结果的分析对比可得出，采用本文的变系数制导方法能够有效减少脉冲发动机的开机次数，合理分配点火时刻并生成脉冲加速度曲线，避免因比例系数N取值不合适造成的在接近目标阶段的频繁开关机。对比结果体现了本文变系数算法较定系数算法在制导性能方面的提升，更适合深空高速撞击任务的工程实施。

为了进一步验证算法在实际应用中的有效性，在考虑误差的情况下进行蒙特卡洛仿真，测量精度如表4所示，误差源量值均为统计意义下参数。

表4 误差源仿真参数Table 4 Parameters of all error source

图10为2 000次蒙特卡洛仿真的撞击误差分布图，采用本文的深空高速撞击变系数末制导律算法的制导误差均方差为83.40 m，最大值为269.07 m，能够满足撞击目标小行星Bennu的需求，总速度增量平均值为9.56 m/s，符合深空高速撞击要求。

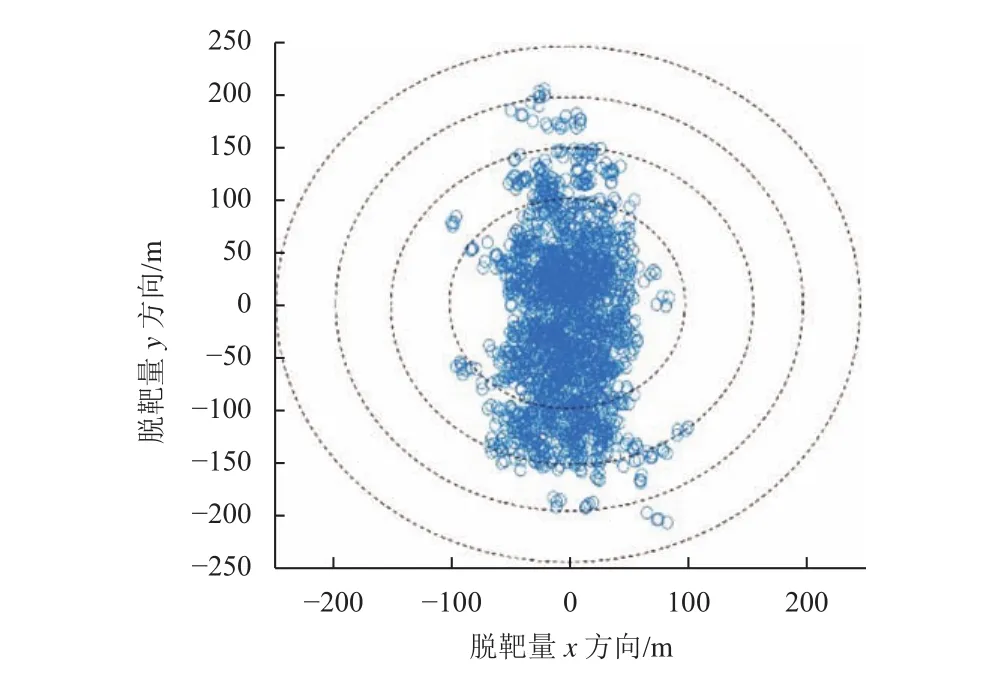
图10 2 000次蒙特卡洛仿真撞击误差分布Fig. 10 2 000 Monte Carlo simulations of impact miss distance distribution

4 结 论

本文针对小行星高速撞击任务相对速度大、撞击精度要求苛刻、携带燃料受限的特点，提出了一种基于增广比例导引的深空高速撞击变系数末制导律。算法在动力学模型中考虑了目标的运动加速度，并通过分析机动时刻与撞击精度、燃料消耗间的关系，将原常值比例系数设计为相对距离的归一化幂函数，任务初期取值较大，随着相对距离的减小，系数随之减小；设计脉冲点火策略，将连续的加速度指令转化为撞击器可直接使用的脉冲加速度指令，无需事先给定撞击器机动时刻。仿真算法以危害度排名前三的小行星Bennu为预设目标，仿真结果展示了算法在考虑测量误差情况下能保证撞击精度，且通过与常值比例系数结果的对比，证明了本文算法能够合理给出系数曲线，明显减少发动机开机次数及所需速度增量，达到节省燃料消耗的目的，具有工程应用的价值。