基于框架理论的最小阵元数稀疏阵综合算法研究 *

陶海红, 郭晶晶

(西安电子科技大学雷达信号处理国家重点实验室, 陕西西安 710071)

0 引言

天线阵列综合问题包括阵型优化和综合权值优化。在天线重量、体积和成本有限时如卫星平台、导航、飞机等，要获得大孔径天线，最小阵元设计是首要考虑的方法[1-7]。

文献[8]的贝叶斯压缩感知 (BCS)[9-10]算法通过将对称阵列优化问题转换为稀疏约束优化框架,并通过贝叶斯压缩感知 (BCS)算法求解,可以有效地减少阵列中的天线元件数量。但文中假设阵元加权只有实部，且阵元分布对称。针对这一问题，文献[11]提出了基于多任务贝叶斯压缩感知算法(multi-task BCS)[12]的最小阵元稀疏阵综合方法，适用于权值为复数，阵列不对称的线阵最小阵元稀疏阵综合问题；文献[13-15]将单任务贝叶斯压缩感知(ST-BCS)以及多任务贝叶斯压缩感知(MT-BCS)应用于最小阵元稀疏面阵、最小阵元稀疏共形阵以及最小阵元稀疏同心圆环阵中，仿真结果都较为理想，但超参数的选择对不同阵元规模的方向图综合问题影响不同，针对不同问题需要做多次实验得到一组适用的超参数，不具有普遍适用性。且在处理面阵问题时，阵元稀疏率只能达到0.64。而本文采用的算法，同一组参数可用于任意规模的线阵与面阵。

本文采用框架理论，将备选阵元位置稀疏化，利用权值的模值大小表示该位置阵元的选择与否，通过次优反馈的零空间追踪硬阈值算法[16]得到满足近似条件的最小l0范数权值解，即得到最小阵元的稀疏阵以及该位置阵元的加权值。线阵与平面阵的仿真结果说明了算法的有效性。

1 阵型的稀疏框架建模

1.1 线阵的稀疏框架问题建模

不失一般性，假设目标为远场窄带信号,模型示意图如图1所示。

图1 线阵示意图

若来波方向θ如图1所示，对于N个阵元的任意线阵，阵列导向矢量可表示为

a(θ)=[a1,a2,a3,…,aN]T

ai=exp(j2πdisinθ/λ),i=1,2，…,N

(1)

式中，λ为波长，di为第i个阵元与参考点之间的距离。

当期望来波方向为θp时，阵列方向图P(θ)可表示为

P(θ)=a(θp)H*a(θ)

(2)

为实现低副瓣要求，一般会在阵元后加权值W，则加权后阵列方向图P(θ)可表示为

(3)

式中,⊙表示矩阵点乘。

(4)

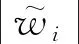
最小化阵元稀疏阵综合问题即可简化为

(5)

1.2 平面阵的稀疏框架问题建模

阵列放置于y0z平面，参考位置为原点，方位角φ和俯仰角θ的定义如图2所示。

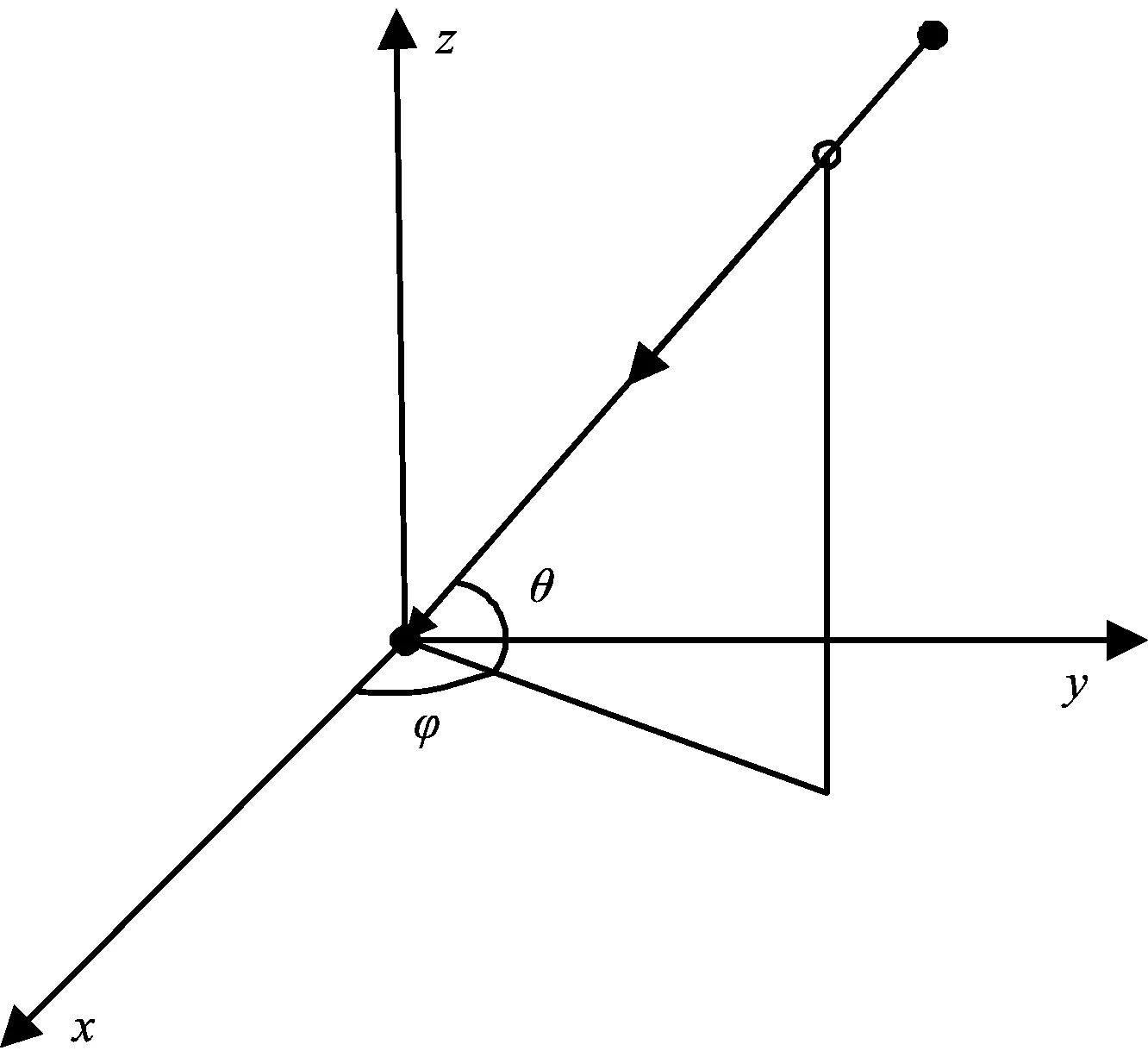
图2 面阵示意图

与线阵类似，N阵元平面阵的普通波束形成方向图可表示为

P(θ，φ)=(a(θp,φp)⊙W)H*a(θ,φ)

(6)

式中,

(7)

其中θp,φp分别为目标俯仰角与方位角，W为阵列加权值，pos为N个阵元在笛卡尔坐标系下的三维坐标矩阵。

假设方位角与俯仰角都取M个值，即P是M*M的复矩阵。

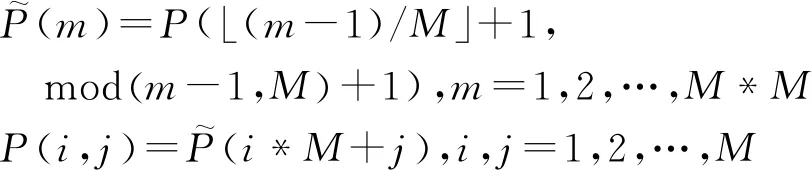
(8)

(9)

最小化阵元稀疏面阵综合问题即可简化为

(10)

1.3 问题模型简化

由于本文算法适用于实数问题，而阵列方向图优化一般为复数问题。只有当参考阵元位置对称时，阵列方向图只有实部，可直接使用第三部分的算法优化得到阵元位置与阵元加权值。其他情况下需将复数问题实数化。

(11)

其中,real(·)表示取实部，imag(·)表示取虚部。

实数化后，问题可重新表示为

(12)

(13)

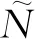
2 次优反馈的零空间追踪硬阈值算法

针对问题

(14)

由于矩阵A是列满秩，行稀疏的，可用针对非凸问题的带反馈的零空间追踪硬阈值算法来实现稀疏约束。

一个零空间追踪基本算法的框架为[16]

(15)

证明：

(16)

(17)

常规硬阈值算法的解为

(18)

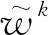
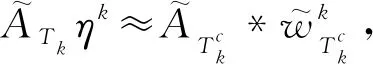
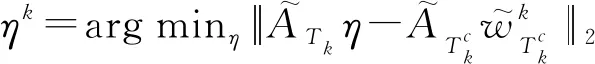
(19)

其最优解为

(20)

算法为

(21)

由于矩阵逆运算的复杂度较高，可将以上算法改进为

(NST+HT+subFB)

(22)

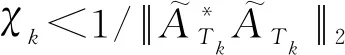
NST+HT+subFB算法流程：

循环B外循环:当H1≻ε1成立，

令H2=1,s=s+1;

内循环: 当H2≻ε2成立，

利用公式(20),计算[wk+1,uk]

内循环结束

外循环结束

将|wk+1|降序排列，取前s个值及其所在位置，得到对应的阵元位置；

由于算法NST+HT+subFB需要在外循环中将稀疏阵元数s从1开始递增，适用于稀疏率较低的问题，即稀疏阵元数目较少。在处理稀疏阵元数目较多或参考阵元数目较多的问题时，计算复杂度高、耗时长且最终效果不太理想。

NST+HT+subFB+cumS算法流程：

循环A: 当H2≻ε2成立，

利用公式(20),计算[wk+1,uk]

若K-s>=s_step

s=s+s_step

循环结束

循环B 外循环:当H1≻ε1成立，

令H2=1,s=s+1;

内循环： 当H2≻ε2成立，

利用公式(20),计算[wk+1,uk]

内循环结束

外循环结束

将|wk+1|降序排列，取前s个值及其所在位置，得到对应的阵元位置；

将NST+HT+subFB算法与NST+HT+subFB+cumS算法统一用流程图即图3表示。

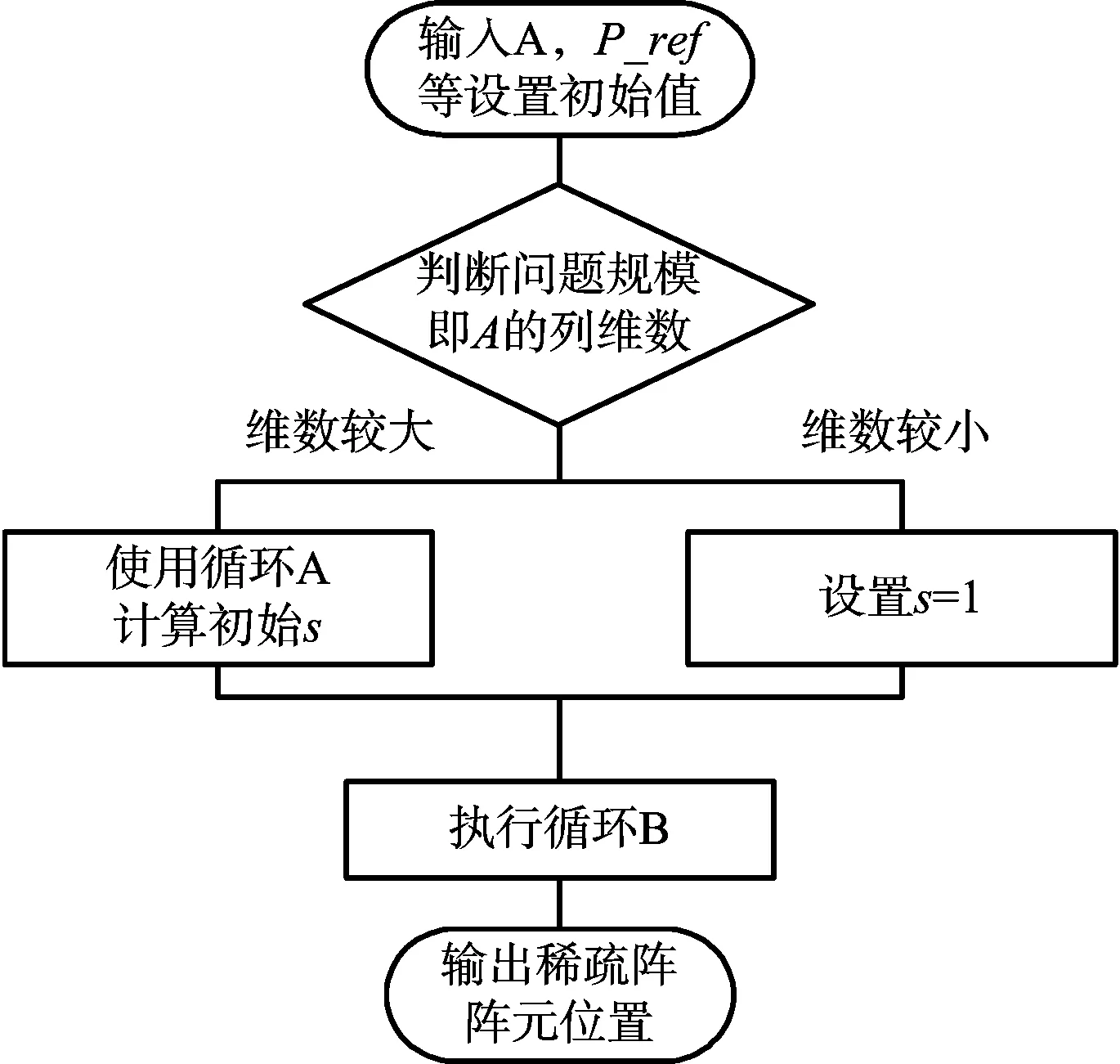
图3 算法框图

3 仿真实验与性能分析

仿真1 不同阵元规模的切比雪夫权值均匀线阵方向图稀疏阵综合

a) 40阵元的切比雪夫权值均匀线阵方向图稀疏阵综合

参考方向图为40阵元切比雪夫权值均匀线阵方向图；备选阵元位置间隔均匀排列为[-25*λ/2:λ/10:25*λ/2]，方向图角度θ∈[-45,45](单位：rad)，仿真结果如图4、图5所示，与参考算法的性能比较如表1所示。

图4 仿真1 a)的方向图

图5 仿真1 a)的阵元位置

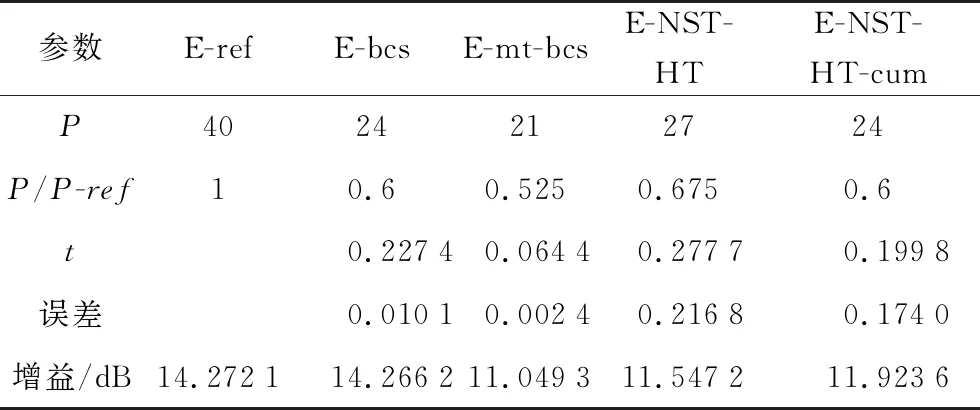
表1 仿真1 a)的4种算法对比

针对参考方向图阵元数目较少情况，所提算法与基于稀疏贝叶斯学习的最小阵元位置优化算法相同，可优化得到符合要求的阵元位置。NST-HT-cum与NST-HT相比，由于首先计算了初始选取元素的数目，加快了算法的速度，误差更小。

b) 300阵元的切比雪夫权值均匀线阵方向图稀疏阵综合

参考方向图为300阵元切比雪夫加权均匀线阵的方向图；备选阵元位置间隔均匀排列为[-150*λ/2:λ/10:150*λ/2]，方向图角度θ∈[-45,45](单位：rad)，仿真结果如图6、图7所示，与参考算法的性能比较如表2所示。

图6 仿真1b)的方向图

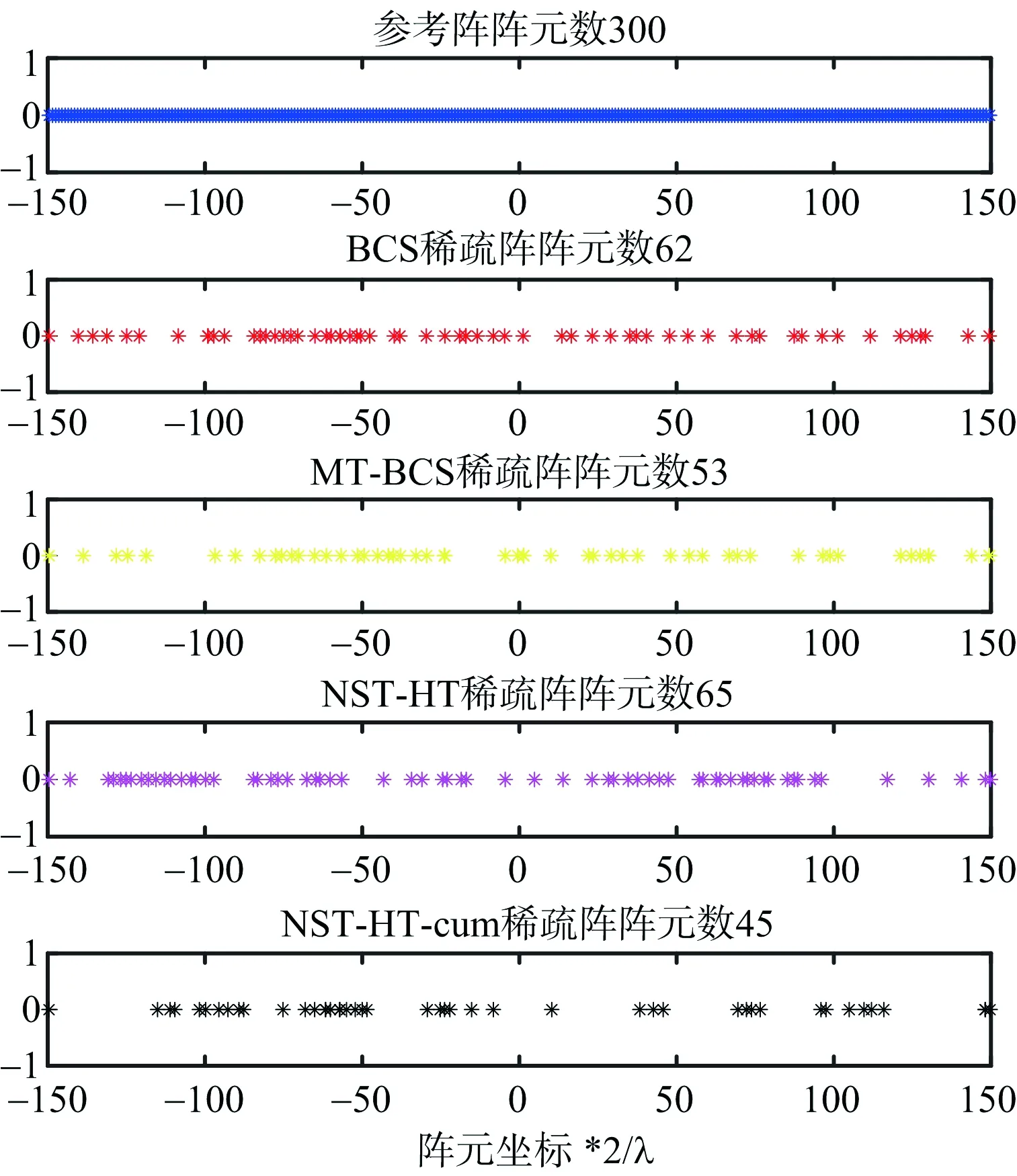
图7 仿真1b)的阵元位置

表2 仿真1b)的4种算法对比

对于参考方向图的阵元数目较大情况，仿真证明了所提算法也可以优化得到满足要求的方向图。与基于稀疏贝叶斯学习的最小阵元位置优化算法相比，在阵元数目增多时，所提算法优势显现。

仿真2 任意方向图的线阵稀疏阵综合

a) 平顶主瓣方向图的稀疏阵综合

参考方向图为给定的平顶主瓣方向图；备选阵元位置间隔均匀排列为[-25*λ/2:λ/10:25*λ/2]，方向图角度θ∈[-90,90](单位：rad)，仿真结果如图8、图9所示，与参考算法的性能比较如表3所示。

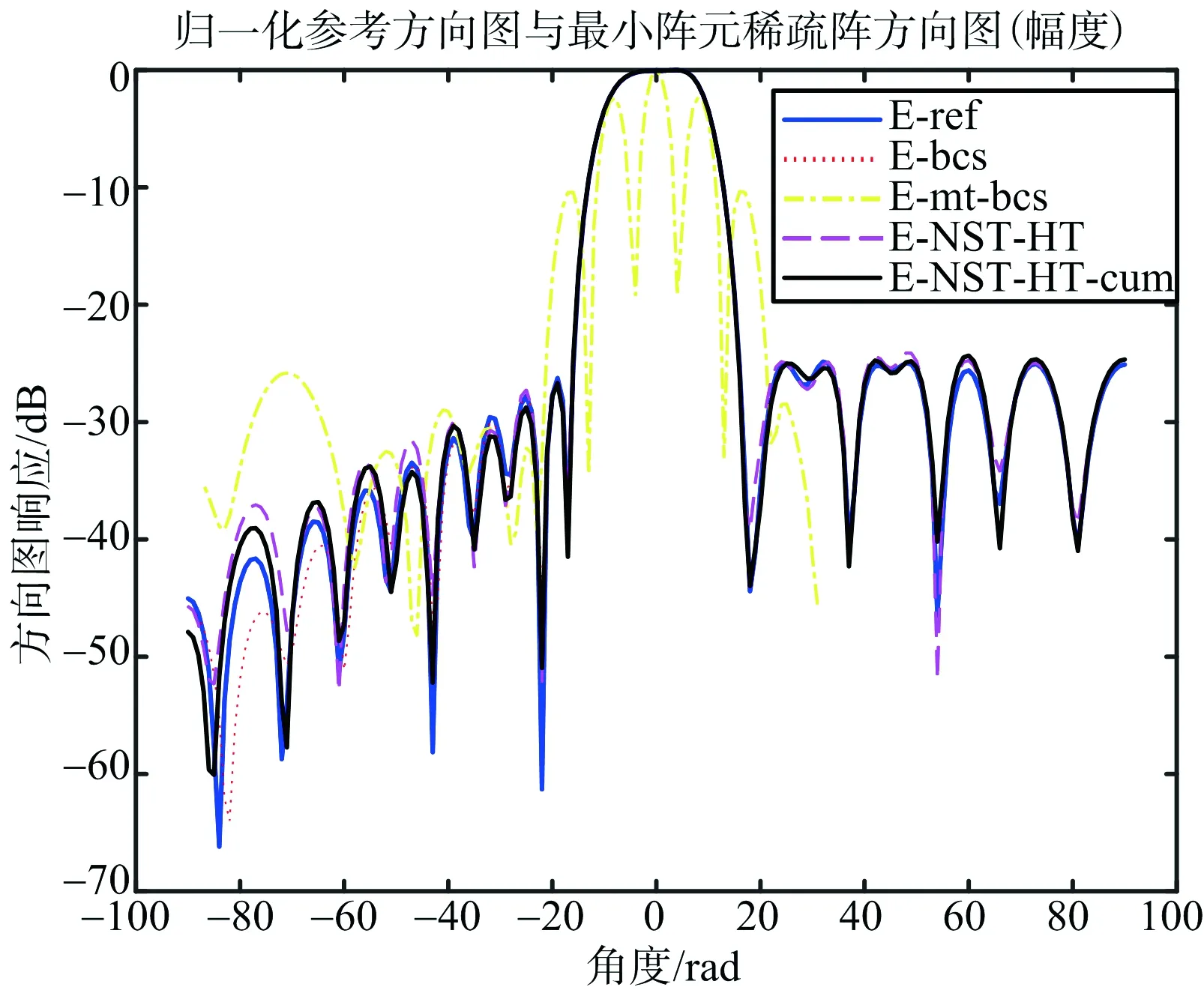
图8 仿真2a)的方向图

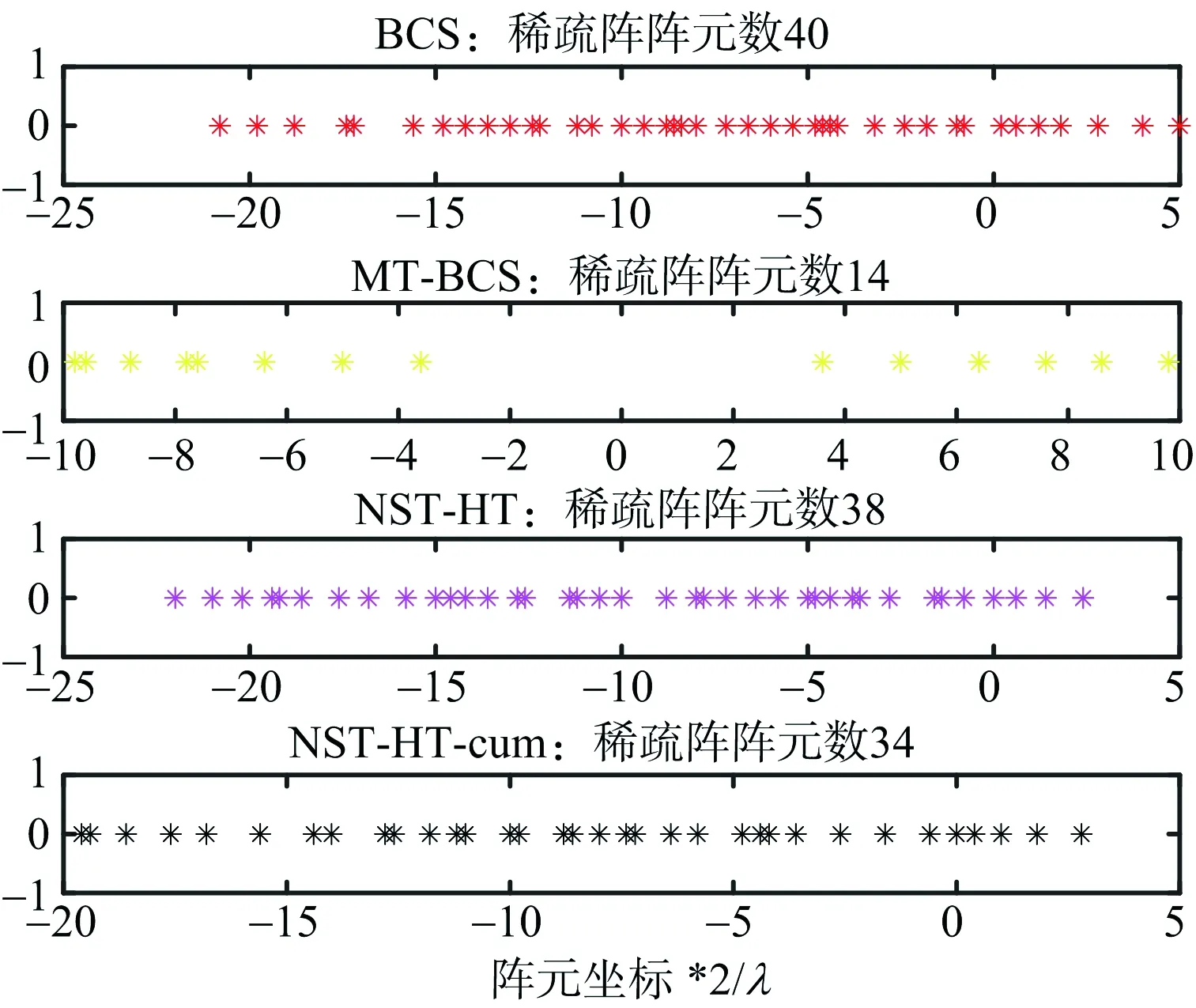
图9 仿真2a)的阵元位置

表3 仿真2 a)的4种算法对比

对于给定的非对称方向图，仿真证明了算法NST-HT与NST-HT-cum的有效性。与基于BCS的优化算法相比，所提算法优化后的阵元数目更少；与基于MT-BCS的优化算法相比，所提算法更加吻合给定的方向图。

b) 双平顶主瓣方向图的稀疏阵综合

参考方向图为给定的双平顶主瓣方向图，主瓣位置为[-45,-35]∪[35,45]；备选阵元位置间隔均匀排列为[-30*λ/2:λ/10:30*λ/2]，方向图角度θ∈[-90,90]，仿真结果如图10、图11所示，与参考算法的性能比较如表4所示。

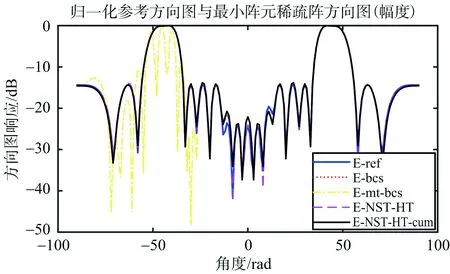
图10 仿真2 b)的方向图

图11 仿真2 b) 的阵元位置

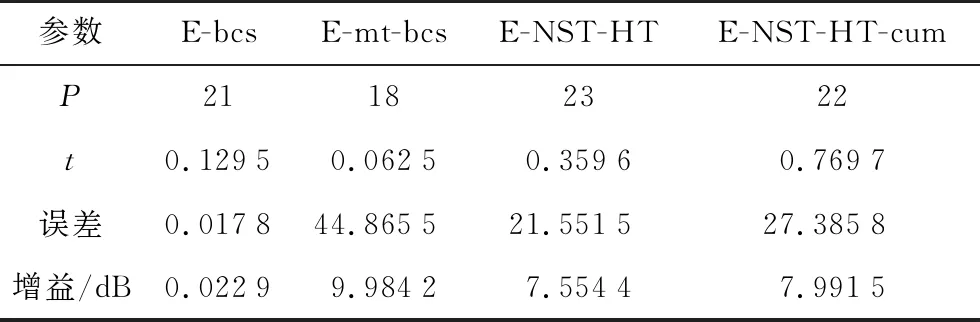
表4 仿真2 b)的4种算法对比

对于给定的双平顶主瓣方向图，算法NST-HT与NST-HT-cum同样有效。与基于BCS的优化算法相比，所提算法的方向图增益更高；与基于MT-BCS的优化算法相比，所提算法更加吻合给定的方向图；算法NST-HT与算法NST-HT-cum的结果相类似。

仿真3 8*8面阵的切比雪夫方向图稀疏阵综合

参考方向图为 8*8的面阵，加权方式为切比雪夫权值；y0z平面备选阵元位置呈栅格分布y∈[-10*λ/2:λ/10:10*λ/2],z∈[-10*λ/2:λ/10:10*λ/2]，方位与俯仰角：θ∈[-45,45],φ∈[-45,45](单位：rad)，仿真结果如图12～图15所示，与参考算法的性能比较如表5所示。

图12 仿真3的方向图

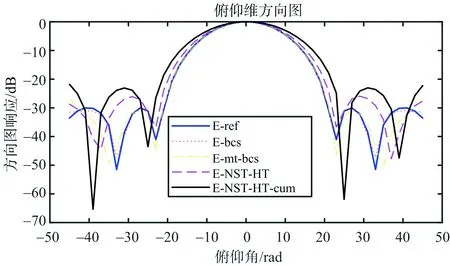
图13 仿真3俯仰维方向图

图14 仿真3方位维方向图

图15 仿真3阵元位置图

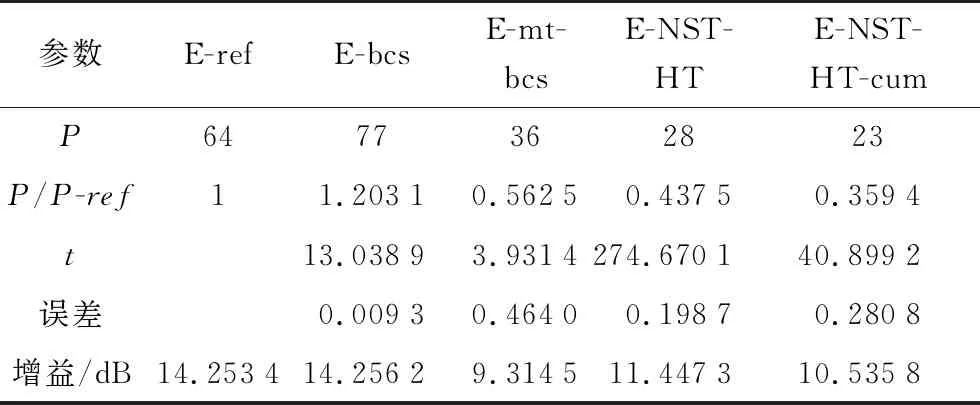
表5 仿真3的4种算法对比

针对给定的8*8平面阵的方向图，所提算法优化结果可在降低阵元数目的情况下，实现低旁瓣方向图综合。基于BCS的算法在处理面阵问题时效果较差。基于MT-BCS的算法可以实现阵元数目的降低，但与所提算法相比误差较大、阵元数目较多且增益低。在备选阵元位置多的情况下，算法NST-HT-cum比算法NST-HT所用时间有明显减少，且优化后阵元数目更少。观察优化得到的4张阵元位置图，不难发现阵元位置似乎是呈现圆形或六边形分布。正如我们所知，圆形或六边形分布阵元的方向图主副比更低。

4 结束语

基于NST-HT的最小阵元方向图综合算法适用于线阵或面阵阵元位置和阵元加权优化问题，可实现符合误差要求的任意给定方向图综合。相比基于BCS和MT-BCS方向图综合算法，所提算法在备选阵元位置较多时，所综合得到的阵元位置更少，误差更小。仿真实验证明了算法的有效性。