用于人工智能的硅基光电子芯片
白冰 裴丽 左晓燕

摘要:提出了利用硅基光电子芯片进行人工神经网络计算处理的方法。硅基光电子芯片凭借光子的独特性质,能够在人工神经网络的计算处理中发挥高带宽、低时延等优势。在处理深度学习中大量的矩阵计算的乘加任务时,硅基光电子芯片拥有更高的处理速度和更低的能耗,从而有利于深度学习中的人工神经网络计算速度和性能的提升。
关键词:人工神经网络;硅基光电子芯片;人工智能;深度学习
Abstract: Silicon photonic chips are used to perform artificial neural network computation. Because of the unique properties of photons, silicon photonic chips have the advantages of high bandwidth and low delay in the computation and processing of artificial neural network. When dealing with the multiplication and addition task of a large number of matrix calculations in deep learning, silicon photonic chips have higher processing speed and lower energy consumption, which is beneficial to the improvement of the computational speed and performance of artificial neural network in deep learning.
Keywords: artificial neural network; silicon photonic chips; artificial intelligence; deep learning
人工智能發展的着眼点之一是强大的大型数据集处理工具。这就要求计算机在没有获得明确指令的条件下,能快速高效地学习并组合分析大量信息。人工神经网络就是可以进行学习的数据处理计算机,而以人工神经网络为基础的深度学习算法因其在图像识别、问题决策、语言翻译、自动驾驶[1]、医疗辅助[2]等方面的应用而受到学术界和工业界的关注。
目前,人工神经网络几乎全部依赖于传统的电域集成芯片,包括中央处理器(CPU)、图形处理器(GPU)、现场可编程门阵列(FPGA)、专用集成电路(ASIC)。微电子芯片因其结构上无法规避的缺陷,在处理大量的矩阵运算时,面临带宽低、功耗大、速度慢等问题,但人工神经网络实现的基础就是大量的矩阵运算;因此,要想实现深度的人工神经网络,就需要更多的时间和能耗成本。我们可以通过不断提高芯片集成度,进行存内计算等方法解决这个问题;但与此同时,晶体管尺寸不断缩小,晶体管的性能也越来越受到量子效应的影响,这限制了集成度的不断提高。另外,存内计算的方法与现有的人工神经网络算法匹配度不高也限制了存内计算这种方法的应用。
为了解决上述问题,学术界和工业界越来越多地致力于开发新的硬件架构,以适应人工神经网络和深度学习的应用。借助光子器件优势(带宽大、速度快),业界提出将一部分信息承载和计算处理用于改善电域芯片存在的问题。相比于传统的三五族或铌酸锂光器件,硅基光电子芯片上的光器件集成在同一硅衬底上,集成度更好且基本与成熟的互补金属氧化物半导体(COMS)工艺兼容。
利用光电子技术实现的人工神经网络主要包括前馈神经网络(FNN)、循环神经网络(RNN)、脉冲神经网络(SNN)3种类型。马赫·曾德尔干涉仪(MZI)和微环谐振器(MRR)具有干涉、谐振等物理特性,可以实现调制器、滤波器等多种器件功能,被广泛地用于通信、传感等领域。目前相对比较完善的、主流的硅基集成通信芯片是基于MZI和MRR的两种类型,因此人工神经网络芯片也主要基于这两种类型。本文中,我们围绕这两种类型对硅基光电子人工智能芯片的进展进行简要阐述,并对未来的发展态势进行展望。
1 利用光网络进行矩阵运算
人工神经网络的思路是首先将输入的事物转化为矩阵,然后经过大量的矩阵运算,最终得到所需要的结果。不同算法的处理流程可能会有一些差异,但是都会包含大量的矩阵运算。矩阵运算的基础就是乘积累加运算(MAC)。在光子领域实现MAC操作并不会在本质上消耗能量,这是光子集成电路的优势之一。
1.1 集成MZI进行矩阵运算的原理
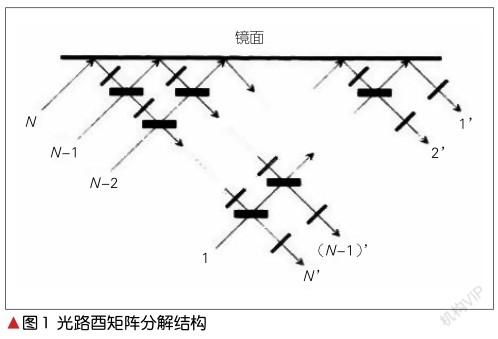
利用MZI进行片上矩阵运算的原理是基于M. RECK等于1994年提出的酉矩阵分解方法[3]的。在该方法中,可调反射率和透过率的分束器和可调的移相器组成基本单元,并通过电压控制分束器的分光比和移相器的相位实现控制输出端口的光强,如图1所示[3]。酉矩阵运算中输入的N×1列向量元素大小由输入光强大小来表示,位置由输入端口的位置表示,输入的多束光分别从入口端MZI的一个臂进入MZI阵列,N×N酉矩阵中的元素使用MZI阵列中每一个MZI包含的2个移相器和分光器的参数来表示。这使得光通过这些MZI时,相位和幅度会发生改变,进而达到计算效果。最后根据输出端的N×1个输出光强大小来计算结果列向量元素大小,元素位置由输出端口的位置表示。在进行输入光强的调制和输出光强的探测后,利用光网络可实现酉矩阵的计算。
图1为光路酉矩阵分解结构。其中,较大黑横矩形表示分光比可调分束器,小黑斜矩形表示移相器,上方细长黑矩形为全反射镜面。
在酉矩阵实现之后,我们可以利用奇异值分解(SVD)的方法对任意矩阵进行分解,即SVD将矩阵分解为2个酉矩阵和1个对角矩阵酉矩阵,光路对角矩阵的模拟用衰减器即可完成,MZI也可以做衰减器。这样就实现了利用MZI进行矩阵运算。


1.2 集成MRR实现矩阵运算的原理
MRR可以先将特定波长的光信号耦合到环上进行调制,然后再耦合进直波导。MRR实现矩阵运算的原理为:通过透过率的调节来实现矩阵的表示。首先矩阵运算中输入的N×1列向量中的元素大小用光强大小表示,列向量中元素的位置由不同的波长表示(因为输入列向量来自于电域信号,所以需要通过调制器进行电光轉换)。M×N矩阵的每一列元素用同一个波长表示,不同列用不同的波长表示,也就是说同一列的MRR耦合的是同一个波长。矩阵的每一行用一个公共波导以及耦合在其上的MRR表示,然后每行上的MRR根据谐振波长的不同,分别对输入的不同波长的光信号进行强度调制以实现乘法器,强度的大小表示的是此行元素的大小,然后MRR再将不同波长的光信号耦合入公共的波导实现加法器。最后矩阵运算结果是一个M×1列向量,其元素大小通过光强大小来表示,然后经光电探测器进行光电转换后,再通过测量电流大小后得到。
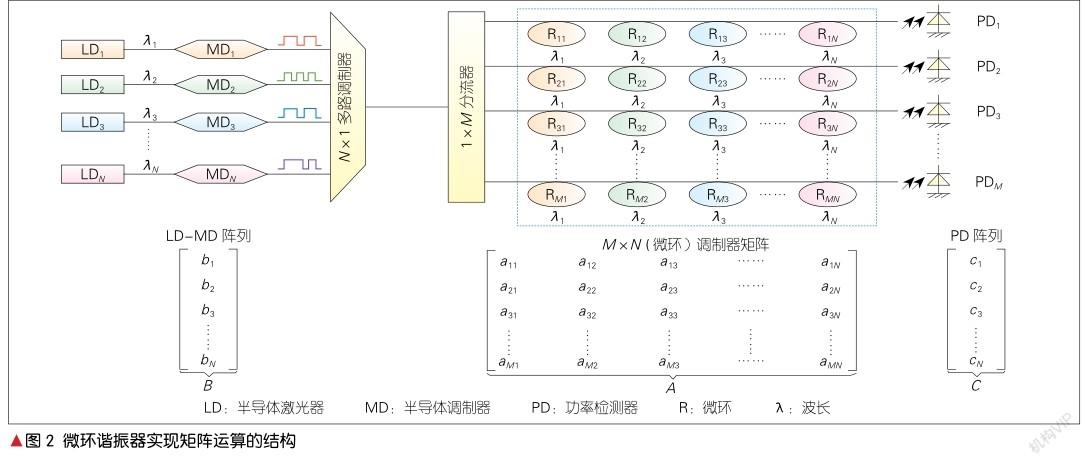
图2所示的是YANG L.等提出的一种利用MRR来实现矩阵运算的方法[4]。这种MRR光网络结构可以执行一个M×N矩阵A和一个N×1向量B的乘法。B是输入向量,用N个不同波长光信号的光功率大小来表示向量B中的元素。这一个列向量B是通过N个外部调制或直接调制激光二极管所生成的。N个光信号通过一个多路复用器被多路复用到一个公共波导上,然后通过一个1×M的光分路器将其平行投影到M行调制器上。矩阵A的aij元素由位于矩阵第i行和第j列的MRR的透射率表示,位于同一行的每个MRR仅对具有特定波长的光信号进行操作。随着M×N光脉冲通过MRR矩阵,光信号就在环上进行了所有的M×N乘法过程。在M个环上进行乘法运算后,其累加过程在公共输出波导中进行。因为不同波长的信号在公共波导中几乎不会互相干扰。结果向量C的元素由光检测器阵列检测到的M个光功率表示。由此,利用MRR进行的矩阵运算便得以实现。
2 现阶段片上人工神经网络的实现
由光来进行矩阵运算是解决人工神经网络需要大量矩阵运算的思路之一。现阶段,硅基集成的、可用于搭建人工神经网络的典型基础器件就是MZI和MRR。通过这些器件的光学特性实现了MAC运算和脉冲神经元的模拟。借助光子数据处理方面的优势,我们将软件和硬件进行深度匹配,使用高效的光电计算取代微电子处理器的计算[5]。光电子集成、数学和软件算法等领域的深度交叉是解决人工神经网络算法大量密集计算问题的路径之一,也是人工神经网络算法片上实现的发展趋向。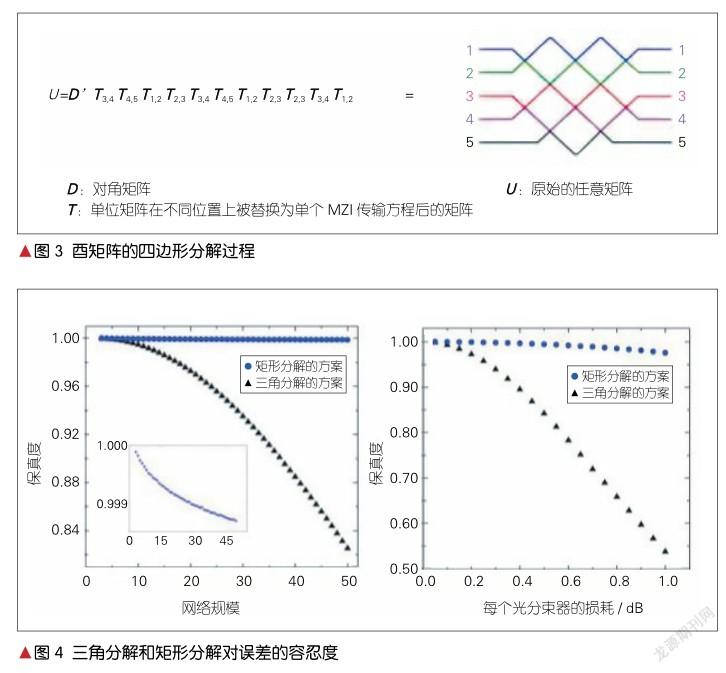
2.1 MZI型片上人工神经网络
在基于MZI构建的前馈人工神经网络中,信息从输入层单向传递到输出层。信号前向传播时,不需要将输出再次反馈,只需要进行加、乘,以及比较操作即可,这与擅长矩阵运算的光网络相匹配;因此,此种方法的光路硬件的实现获得了广泛的探索和关注。虽然M. RECK等发现以MZI进行酉矩阵的分解方法时并未考虑集成[3],但是MZI型人工神经网络日渐向集成发展。W. R. CLEMENTS等在2016年基于M. RECK等的三角分解法提出了矩形分解法[6],将MZI进行重新排布来实现酉矩阵运算。通过将MZI的排布形状从三角转化为矩形,减少一半的光学深度,同时也增加了计算网络的误差容忍度。酉矩阵的分解过程如图3所示。酉矩阵矩形分解方法比酉矩阵三角分解方法更有优势。这是因为酉矩阵三角分解方法的光路是不对称的,从而导致了一些传输过程中的误差。矩形设计减小了线路不对称性,并缩短了最长链路的长度,从而减少了光传播的路径损耗和误差。在对500个随机生成含误差酉矩阵传输的模拟中,随着酉矩阵规模N从2扩大到50,三角分解方法的准确度由100%下降到约82%;但是矩形分解方法的准确度并未发生明显下降,一直保持在约100%,具体如图4所示。
2017年,SHEN Y. C.等利用56个MZI实现了可以用于元音识别的全连接片上神经网络,制成了光子干涉单元芯片。芯片的部分结构如图5所示[7]。在这个设计中,通过MZI阵列进行神经元线性部分的运算,人工神经网络中的非线性激活函数采用电域仿真的方法得以实现,最终可实现全连接神经网络的片上系统。该芯片搭建了2层、每层4个神经元的全连接神经网络。图5所示的芯片结构只有1个酉矩阵和1个对角阵,所以应用时要先将元音信号转为光信号,取得结果放到电域中处理为光信号再传进来,至此完成一层计算。将以上过程循环两遍即为2层神经网络。上述结构在对4个元音的分类的实验中,能够从大量不同元音的语音信号中正确识别和分类元音,准确率达到76.7%。
2019年,M. Y. S. FANG等研究了两种类型的MZI神经网络,分别为GridNet(网格网络)、FFTNet(快速傅里叶变换网络),其物理结构如图5所示[8]。其中,矩阵的分解采用的是SVD。FFT酉矩阵乘法器是非通用性的乘法器,它由Cooley-Tukey FFT算法启发而来,用牺牲通用性的方式来换取结构上的紧凑性。由图6可以看出,GridNet和四边形结构是同一种结构,它和FFTNet结构皆为8×4的线性矩阵运算器。这两种结构均为仿真,在零误差的情况下,GridNet的准确率约为98%,FFTNet的准确率约为95%,因此零误差时的GridNet准确率比FFTNet的准确率高;但是在有差错的情况下,FFTNet的容错率要比GridNet高。在综合误差从0升高到0.02时,FTTNet的准确率由约95%降到约93%,而GridNet的准确率由约97%降到约48%。越小的网络差错传播所带来的误差就会越小,这导致了FFTNet的稳定性要优于GridNet。
综上可得,无论是在矩阵规模扩大还是误差增加的情况下,三角结构的准确率低于矩形结构。矩形结构和GridNet是同种结构,它和FFTNet结构各有利弊:GridNet结构的通用性好,但在存在误差的情况下,准确率低;FFTNet通用性差,但在误差存在的情况下,准确率高。
2.2 MRR型片上人工神经网络
MRR神经网络主要用来实现脉冲神经网络(SNN)。这种网络考虑了时间信息,相比于FNN和RNN更加接近于真实的人脑运作情况,被称为第3代神经网络[9]。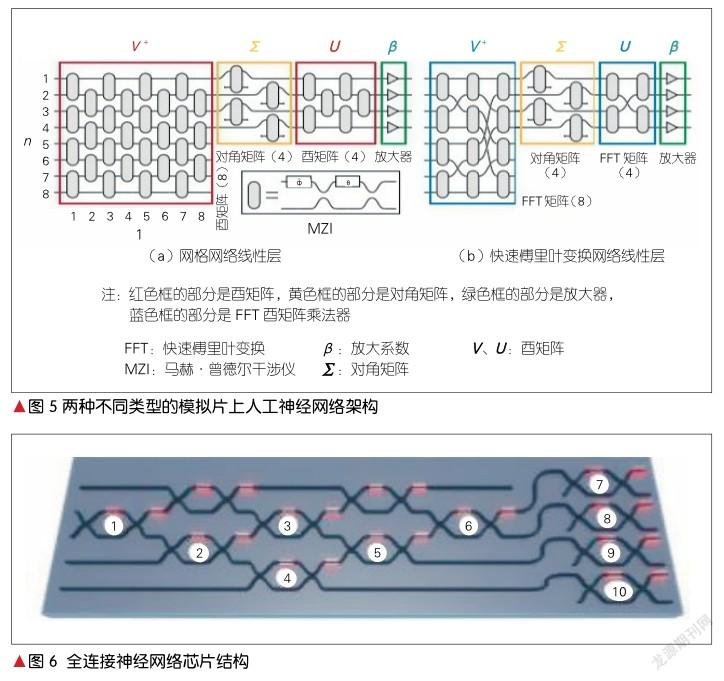
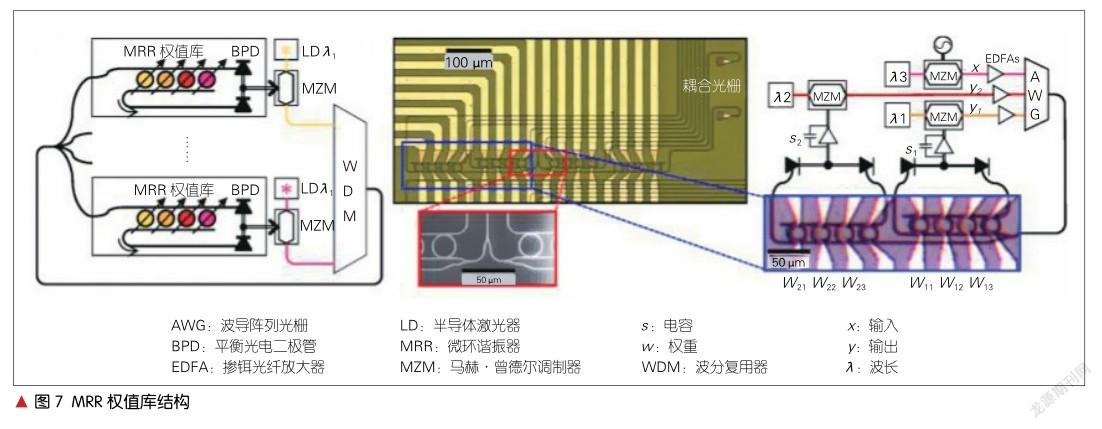
图7所示为A. N. TAIT等于2017年提出的一种广播式MRR权值库结构的神经网络 [10]。这是一种以MRR调制器作为神经元,由MRR权值库连接而成的网络。每一个MMR都承担着一个权值,每一横条聚集在一起的MMR叫权值库。该芯片结构包含4个节点,带有16个MRR。该结构证明了硅光子电路与连续神经网络模型之间存在数学同构关系。根据这种同构性,我们利用“神经编译器”对一个模拟的24节点硅光子神经网络进行编程,完成了微分系统仿真任务。根据推算,与传统的解决相同问题的CPU相比,此结构的处理速度将提高294倍。
2019年,A. N. TAIT等提出了一种神经拟态的片上结构[11],该结构主要由2个光探测器和1个MRR组成,如图8(a)所示。神经元阵列由电脉冲强度调控单元及延时单元构成,除泵浦激光器外,整体网络可实现片上集成。每个MRR只有一个波长(λi)。该结构将MRR强度调制器和平衡的光电探测器组成电光脉冲强度和延迟调控单元,并使用电光脉冲进行调控,以实现复杂的脉冲神经网络。当输入为2 ns脉冲偶极子,第2次的输入相比于第1次输入延迟一个波长,进而产生t = 0时的脉冲重合。据此测得的加强、饱和、抑制3种情况下的结果如图8(b)所示。在图8(b)中,在可见增强情况下,脉冲出现过冲现象(超过57%);而在饱和情况下,脉冲只为输入脉冲和的56%,且单脉冲抑制不完全。虽然存在一些问题,但是这种结构形成了全光广播权值神经网络的组件类型,在一个集成的光子组件中包含了光到光的非线性、扇入和非确定性级联,实现了光子神经元的网络兼容的能力。
目前MRR人工神经网络偏向于贴合神经网络的数学同构模型的研究,采用比较统一的采用扇入结构、光电光转换等实现方案。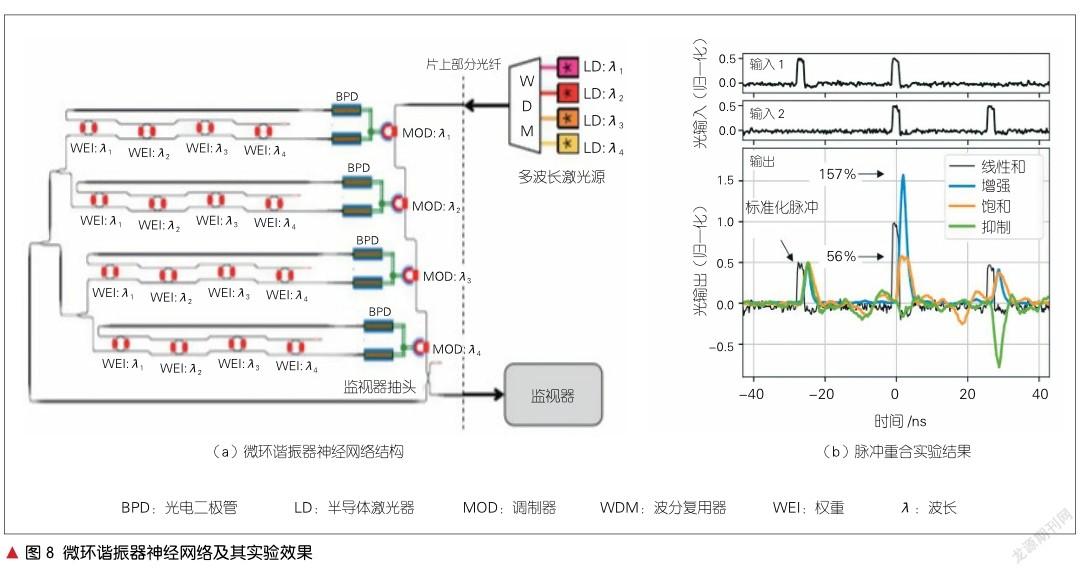
2.3 MZI型与MRR型片上人工神经网
络的对比
MZI型片上人工神经网络是根据酉矩阵分解和计算来设计数学同构性的;而MRR型片上人工神经网络则直接以普通矩阵的计算来设计数学同构性。两者本质上都是用光器件来表现数学计算。由于MRR型仍在结构探索阶段,相比于MZI型,准确性远远不足;而MZI型有较为成熟的应用测试,但相比于传统芯片,准确性仍有不足。
3 片上人工神经网络实现方案面临的挑战
利用光子进行计算具有诸多优势,但目前仍存在一些问题:
(1)非线性激活函数是用来增加神经网络非线性的一种S形状的函数,它的硬件实现起来比较困难。现在非线性函数的实现方式分为两种:一种就是转换到电域再处理[7]或利用电域辅助处理[12];另一种就是利用特殊材料,如可饱和吸收体和石墨烯等进行处理。一方面,光电转换限制了数据处理速度的进一步提升;另一方面,大部分特殊材料的片上集成较为困难,不能与互补金属氧化物半导体(CMOS)工艺兼容。
(2)MZI的长度约为200 μm,MRR的长度约为25 μm。相比于电域的器件,芯片集成度差,目前工艺方面还有进一步提升的空间。虽然看起来MRR要比MZI小一些,但是它们基本都属于一个数量级。另外,由于目前硅基集成光器件的工艺仍旧不够成熟,器件的一致性、穩定性较差。
(3)目前我们需要对光电人工智能芯片的匹配算法和外围电路进行设计[13],并需要将各领域技术深度融合。这个结合的过程需要重新进行布局和设计,在目前没有统一标准的情况下。每一个光网络结构的出现都可能会导致外围匹配的电路和算法重新被调整和优化。
4 结束语
光电神经网络能够利用光子技术的优点并配合外围电域进行处理,在提升计算速度的同时也可以降低运行功耗。无论是基于FNN的MZI前向人工神经网络芯片,还是基于SNN的MRR神经拟态人工神经网络芯片,都可以利用硅基光电子技术进行实现。此外,光电神经网络亦会随着硅基光电子技术的成熟而不断取得突破,如硅基片上光源、放大器、硅基单片集成、硅基新材料融合等新型硅基光电子技术,都将为光电神经网络的物理研究提供崭新的、开阔的思路。同时,随着与光电神经网络相匹配的算法演进,相信在将来的研究中,硅基光电子技术、硅基光电子芯片将为人工智能领域带来全新的技术架构和重大的产业升级。
参考文献
[1] AL-QIZWINI M, BARJASTEH I, AL-QASSAB H, et al. Deep learning algorithm for autonomous driving using GoogLeNet [C]//2017 IEEE Intelligent Vehicles Symposium (IV). Los Angeles, USA: IEEE, 2017. DOI:10.1109/ ivs.2017.7995703
[2] ESTEVA A, KUPREL B, NOVOA R A, et al. Dermatologist-level classification of skin cancer with deep neural networks [J]. Nature, 2017, 542(7639): 115-118. DOI: 10.1038/nature21056
[3] RECK M, ZEILINGER A, BERNSTEIN H J, et al. Experimental realization of any discrete unitary operator [J]. Physical review letters, 1994, 73(1): 58. DOI:10.1103/physrevlett.73.58 DOI:10.1103/physrevlett.73.58
[4] YANG L, JI R Q, ZHANG L, et al. On-chip CMOS-compatible optical signal processor [J]. Optics express, 2012, 20(12): 13560. DOI:10.1364/oe.20.013560
[5] 白冰, 趙斌, 杨钊. 一种光子神经网络芯片以及数据处理系统: CN110503196A [P]. 2019-11-26
[6] CLEMENTS W R, HUMPHREYS P C, METCALF B J, et al. Optimal design for universal multiport interferometers [J]. Optica, 2016, 3(12): 1460. DOI:10.1364/optica.3.001460
[7] SHEN Y C, HARRIS N C, SKIRLO S, et al. Deep learning with coherent nanophotonic circuits[C]//2017 IEEE Photonics Society Summer Topical Meeting Series (SUM). San Juan, USA: IEEE, 2017: 441-447. DOI:10.1109/ phosst.2017.8012714
[8] FANG M Y S, MANIPATRUNI S, WIERZYNSKI C, et al. Design of optical neural networks with component imprecisions [J]. Optics express, 2019, 27(10): 14009. DOI:10.1364/ oe.27.014009
[9] MAASS W. Networks of spiking neurons: the third generation of neural network models [J]. Neural networks, 1997, 10(9): 1659-1671. DOI: 10.1016/s0893-6080(97)00011-7
[10] TAIT A N, DE LIMA T F, ZHOU E, et al. Neuromorphic photonic networks using silicon photonic weight banks [J]. Scientific reports, 2017, 7: 7430. DOI: 10.1038/s41598-017-07754-z
[11] TAIT A N, DE FERREIRA L T, NAHMIAS M A, et al. Silicon photonic modulator neuron [J]. Physical review applied, 2019, 11(6): 064043. DOI: 10.1103/physrevapplied.11.064043
[12] WILLIAMSON I A D, HUGHES T W, MINKOV M, et al. Reprogrammable electro-optic nonlinear activation functions for optical neural networks [J]. IEEE journal of selected topics in quantum electronics, 2020, 26(1): 1-12. DOI:10.1109/jstqe.2019.2930455
[13] 白冰, 赵斌, 杨钊. 一种计算电路以及数据运算方法: CN110597756A [P]. 2019
作者简介
白冰,北京交通大学光波技术研究所在读博士研究生;主要从事硅光集成计算器件、光电异构计算架构和光电融合神经网络算法等领域的研究;已申请专利12项。
裴丽,北京交通大学教授、博士生导师;主要从事全光交换、特种光纤、光电器件及基于智能光纤传感的物联网的研究;主持科研项目10余项,发表SCI、EI论文200余篇。
左晓燕,北京交通大学光波技术研究所在读博士研究生;主要从事光神经网络、光电器件领域的研究。

