沈阳市东塔桥地震响应分析
董成

摘 要:沈阳市东塔桥为采用格构式钢桥塔钢箱梁的自锚式悬索桥。为减小地震效应,该悬索桥设置了黏滞阻尼器。本文以该桥为研究对象,建立全桥的动力计算模型,对此桥的动力特性进行计算分析,同时对比有阻尼器及无阻尼器下的动力响应,分析相应工况下的减震率,研究黏滞阻尼器对该桥抗震性能的影响。
关键词:自锚式悬索桥;时程分析;黏滞阻尼器
中图分类号:U448.25文献标识码:A文章编号:1003-5168(2021)14-0077-03
Abstract: Shenyang East Tower Bridge is a self-anchored suspension bridge with steel box girder of lattice steel tower. In order to reduce the seismic effect, the suspension bridge is equipped with viscous dampers. This paper takes the bridge as the research object, establishes a dynamic calculation model of the full bridge, and calculates and analyzes the dynamic characteristics of the bridge, and compares the dynamic response with and without dampers, analyzes the damping rate under corresponding working conditions, and studies the effect of viscous dampers on the seismic performance of the bridge.
Keywords: self-anchored suspension bridge;time history analysis;viscous damper
随着我国交通运输业的发展及城市化进程的加快,城市交通干线变得越来越重要,大跨径自锚式悬索桥以其造型优美、材料强度高、结构整体自重轻和便于制造等特点往往应用于交通干線的重要节点。同时,我国地震灾害频发,地震作用直接影响桥梁结构安全,因此,正确分析大跨度自锚式悬索桥的地震响应,并对其规律进行把握,采取相应的减隔震措施,对确保桥梁安全具有重要意义[1-2]。
1 概述
东塔桥位于沈阳市祝科街,跨越浑河。主桥为五跨连续采用格构式钢桥塔钢箱梁的自锚式悬索桥,主桥桥梁跨径布置为40 m+90 m+220 m+90 m+40 m。悬索桥主梁采用整体式长挑臂扁平钢箱梁结构,钢箱梁梁高为3 m,锚固段梁高局部加厚为4.8 m。主桥有索区钢箱梁宽为43.3 m,无索区宽为40 m。悬索桥主缆垂跨比为1.0/5.5,主缆在横桥向的间距为36 m,主缆锚固于边跨钢梁上。主桥塔在洪水位以上采用钢桁架结构,洪水位以下为钢筋混凝土塔座。桥面以上塔高为45.05 m,主塔中心横桥向间距为36 m,塔座为钢筋混凝土结构。桥塔承台厚度为5.0 m,桩基直径为2.0 m;引桥墩承台厚度为2 m,引桥桩基直径为1.2 m。钢结构采用Q345D低合金钢板;桥墩、桥台采用C40混凝土;承台及钻孔桩采用C30混凝土。
2 动力模型建立及技术指标
2.1 动力计算模型建立
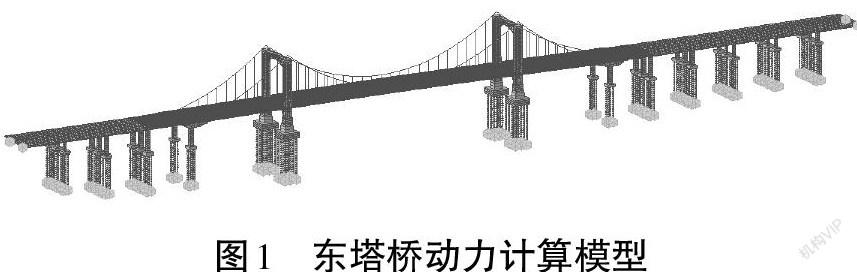
采用有限元程序建立全桥动力计算模型,主梁采用脊梁模型;采用索单元模拟主缆及吊索,主塔、桥墩、桩基采用梁单元模拟;桩周考虑桩-土的相互作用,采用弹性连接模拟土的刚度,黏滞阻尼器采用Maxwell模型模拟[3-4]。全桥动力计算模型如图1所示。
2.2 技术指标
沈阳市抗震设防烈度为Ⅶ度;设计基本地震加速度为0.10g(g为重力加速度),设计地震分组为第一组,设计特征周期值为0.35 s;桥梁抗震设防类别为A类;桥梁抗震设防措施等级为8度;主桥采用普通球形钢支座,在主塔牛腿位置与主梁间设置黏滞阻尼器。
黏滞阻尼器的阻尼力为2 200 kN,速度指数为0.4,阻尼系数为2 200 kN·s/mm,位移值为±30 cm;桩基考虑桩-土作用,采用m(m为土的水平抗力系数的比例系数)法。
3 桥梁动力特性计算结果
3.1 自振特性分析
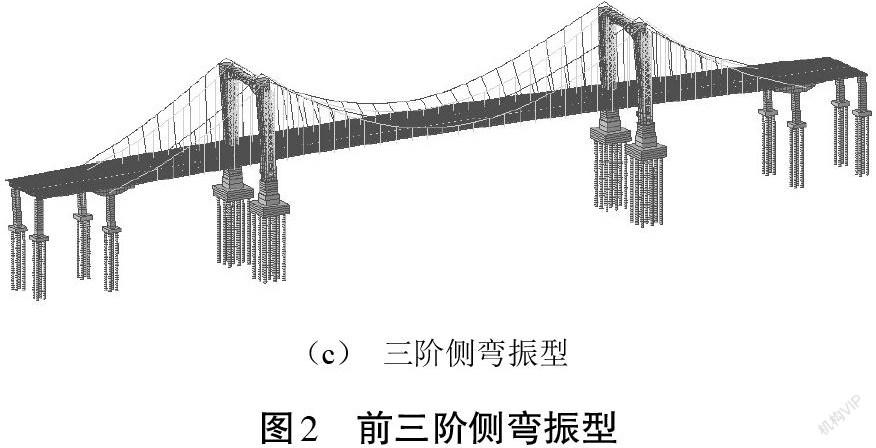
下面用利兹向量法计算参与组合计算的振型。振型组合采用完全二次振型组合(CQC)法,计算150阶自振频率,振型x、y、z各方向参与质量均大于95%[5]。通过对设置黏滞阻尼器及未设置黏滞阻尼器的桥梁结构分别进行特征值分析可得,主要振型的频率及周期如表1所示。桥梁结构设置黏滞阻尼器,前三阶振型如图2所示。
3.2 地震时程分析
在上述桥梁有限元模型的基础上,下面采用图3所示的三条地震波作为地震动输入,分别对桥梁进行地震时程响应分析。
分别对设置黏滞阻尼器及未设置黏滞阻尼器的桥梁结构的桥塔根部控制内力(剪力、弯矩)、桥塔顶部位移、主桥梁端位移进行对比,如表2至表4所示。
在地震波荷载作用下,分别对设置黏滞阻尼器及未设置黏滞阻尼器的桥梁结构进行计算。由桥塔根部地震响应结果可知,设置黏滞阻尼器情况下塔底根部剪力较未设置黏滞阻尼器情况下减小13.5%~54.7%,设置黏滞阻尼器情况下塔底根部弯矩较未设置黏滞阻尼器情况下减小58.8%~82.3%;由桥塔顶部地震响应结果可知,设置黏滞阻尼器情况下桥塔顶部纵向位移较未设置黏滞阻尼器情况下减小22.8%~82.0%;由主梁两端部的纵向位移结果可知,设置黏滞阻尼器情况下主梁两端纵向位移较未设置黏滞阻尼器情况下减小44.6%~84.2%。
通过上述三项主要动力响应对比结果可知,黏滞阻尼器对桥梁结构的减震效果明显。
4 结语
本文分析了东塔桥桥梁结构在地震荷载作用下的响应,对比了设置阻尼器及未设置阻尼器的桥梁结构响应分析结果。研究结果表明,黏滞阻尼器对东塔桥的前三阶动力特性有比较明显的影响,在桥塔与主梁间增设黏滞阻尼器,可以有效减小塔顶位移、塔底弯矩和塔底剪力,改善桥塔受力状态,同时有效减少梁端位移的地震响应,达到了较好的减震效果。
参考文献:
[1]范立础.桥梁抗震[M].上海:同济大学出版社,1997:4-19.
[2]李建慧,李爱群.空间缆索自锚式悬索桥计算、监控和评估[M].北京:人民交通出版社,2011:6-17.
[3]交通部.公路桥涵地基与基础设计规范:JTG D63—2007[S].北京:人民交通出版社,2007.
[4]陈永祁,耿瑞琦,马良喆.桥梁用液体粘滞阻尼器的减振设计和类型选择[J].土木工程学报,2007(7):56-60.
[5]住房和城乡建设部.城市桥梁抗震设计规范:CJJ 166—2011[S].北京:中国建筑工业出版社,2011.

