七自由度模块化机械臂工作空间优化研究

郑威特 杨阳 王大中 王琦 许凯元

摘要： 针对两种长度相同构型不同的七自由度模块化机械臂，研究其工作范围的空间优化问题。首先运用了DH法则进行手臂结构建模，得到了正运动学模型并分析了位姿变换矩阵;在模拟仿真软件的基础上，构造了双臂的结构，利用蒙特卡罗方法求解了工作空间，并利用软件绘制了两种手臂构型的三维工作空间;最后利用数据指标对比分析两种手臂构型的工作空间以及结构效率，比较了两种机械臂构形的差异，获得最优构型，为进一步研究机械手最优构型以及优化工作空间奠定了基础。

关键词： DH法则; 蒙特卡洛法; 七自由度机械手;工作空间优化; 三维仿真工作空间

中图分类号：TP18      文献标识码：A

文章编号：1009-3044（2021）28-0144-05

開放科学（资源服务）标识码（OSID）：

Research on Workspace Optimization of 7-DOF Modular Manipulator

ZHENG Wei-te， YANG Yang， WANG Da-zhong， WANG Qi， XU Kai-yuan

（Shanghai University of Engineering Science，Shanghai 201620， China）

Abstract： Aiming at two kinds of 7-DOF modular manipulators with the same length and different configurations， the space optimization of their working range is studied. Firstly， DH rule is used to model the arm structure， the forward kinematics model is obtained， and the pose transformation matrix is analyzed; Based on the simulation software， the structure of the two arms is constructed， the workspace is solved by Monte Carlo method， and the three-dimensional workspace of the two arm configurations is drawn by the software; finally， the workspace and structural efficiency of the two arm configurations are compared and analyzed by using the data index， and the differences between the two arm configurations are compared， so as to obtain the most efficient results The optimal configuration lays a foundation for the further study of the optimal configuration of manipulator and the optimization of workspace.

Key words： DH rule; monte carlo method; 7-DOF manipulator; workspace optimization; 3D simulation workspace

模块化机械臂是以标准化模块库为基础，可以根据具体不同的任务要求自定义装配设计完成要求目标的自由构型机械臂。还可以针对模块化机械臂构型数学表达、运动学、动力学、面向任务的构型优化设计和轨迹规划等问题。机械手的工作空间范围既末端执行器上能够到达的所有点的集合。在机械手的设计和应用过程中，工作空间点云图在优化机械臂分析研究中起到了举足轻重的地位，此外还需要对工作空间进行比对分析，例如机械手单位长度的空间体积和工作空间的灵活性等工作空间参数是衡量机械手工作能力的重要指标。

数值法、解析法和几何法，这三种是比较常用的工作空间求解方法。第一种数值法相对另两种方法较为实用及便捷，主要以极值理论为基础，较为灵活并借助计算机运算能力以及可视化;解析法的求解过程比较复杂，涉及逆运动学等问题，在实际应用中不具有实用性;在解决三自由度以下的机械手的问题常采用几何法，几何法更简单直观。国内外研究人员也充分研究了求解机械臂工作空间，赵亚川等人分析传统蒙特卡洛法在应对超冗余机械臂时存在的不足，引入基于k- NN（ k近邻）的点云边界提取方法，改善了蒙特卡洛法计算中存在的点分布不均、点云生成速度慢和点云边界提取困难等问题，最后将改进的方法应用于蛇形机械臂的工作空间求解并证实其计算效率及实用价值;刘彦伯使用的方法是快速极坐标搜索法来对机器人的工作空间进行了分析[2];柯江岩等人[3]通过机器人正运动学建模，获取运动云图节点，提取分拣机器人复杂工作空间边界曲线，根据边界曲线中空间节点排列方式，给定性能优化运动指标，求解机器人分拣行为逆运动学，得到求导与定义最优组合解，确定机器人工作空间外界范围曲线;叶鹏达等人[4]首先，结合矢量法与旋转矩阵推导得出并联机器人位置反解的全解析表达式，并在Mathematica中构建了并联机器人虚拟样机，通过算例仿真验证了位置反解数学模型的正确性[1];然后，在考虑杆长约束的全解析位置反解的基础上，采用有限离散法求得并联机器人在三个不同位置的工作空间;鲁凯等人[5]采用圆弧相交法求定姿态的工作空间，得到截面形状，利用梯形积分法计算出工作空间体积;崔建昆等人[6]提出一种平面并联机器人工作空间新的表达方法采用迭代搜索法，以运动方程逆解为判别式，进行工作空间的圆周式搜索，得到了全姿态工作空间的三维展示，并对其特性进行研究，在此基础上，得到了在工作空间内无空腔的杆长到达工作空间的比值;Morteza Alebooyeh等人[7]利用人工神经网络，使得其在一个可接受的置信区间内预测逆运动学解并利用神经网络工具箱在MATLAB平台上建立数学模型，包括所有运动学模型，即机械手关节和连杆的物理结构，并进行可视化表示;Lucian Milicad等人提出了一种机器人几何模型和工作空间传感的新方法[8]，根据空间链闭合方程的一般方法，建立了空间链的正、逆几何模型，将六维空间划分为两个三维空间，即平移空间和旋转空间。根据设计初期的要求，通过特定的算法得到6D空间的二维横截面和工作空间的直观表示。最后，讨论了三种分离方法与刀具在某一加工过程中所施加轨迹的关系。

本文主要针对相同长度下不同构型的七自由度机械臂进行优化分析：a）进行运动学分析，并得到了运动学模型;b）对两性结构的机械臂通过仿真建模软件进行建模，为分析得出最优结构，可运用蒙特卡洛法分别获得两机械手臂的可视化点云图c）再采用各项指标分析判断机械臂的优缺点。

1 机械臂运动学模型分析

1.1机械臂模型及其坐标系

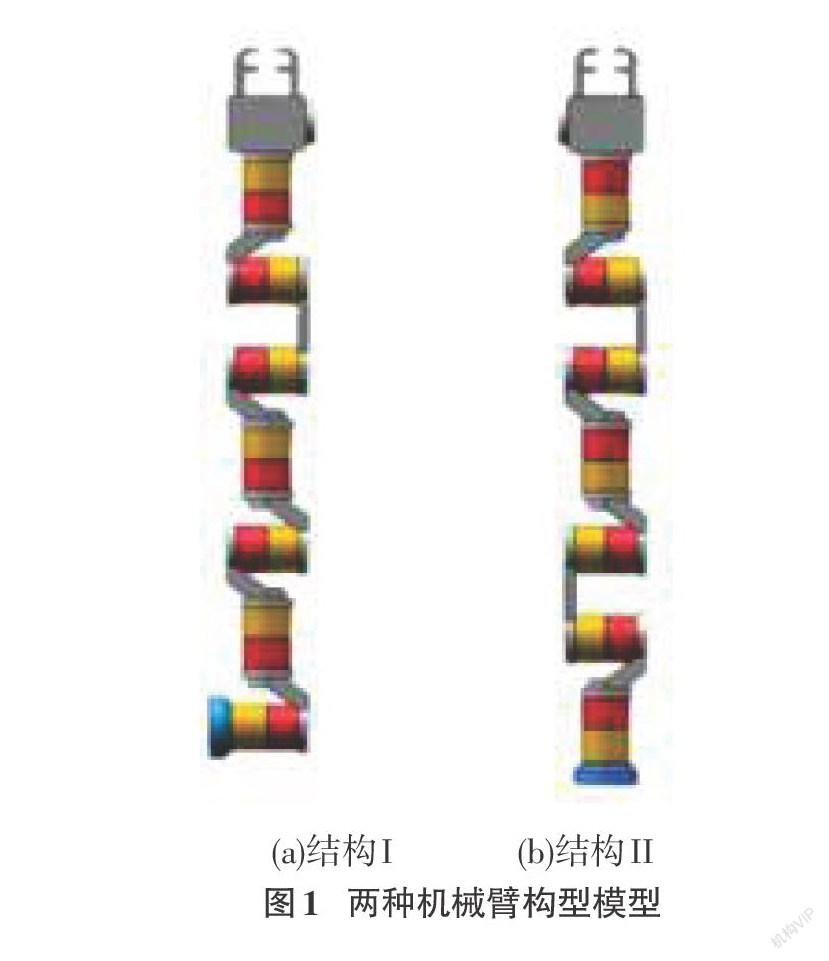
本文中出现的机械手是自行设计的两种七自由度构型机械臂。图1和图2分别展示了两种构型机械手的模型以及机械手构型对应的坐标系。

1.2 确定结构参数

本文分析研究的两种机械臂均有七个旋转关节，两种结构的完整坐标系如图2所示，且根据其构型特点，通过DH法则建立坐标系，将坐标原点分别设在构型1的关节1处以及构型2的关节2处，其对应的DH参数分别由表1和表2所示。

1.3位姿变换矩阵分析

连续连杆之间的坐标关系由图3所示，显示了连杆n-1和连杆n之间的坐标关系的转换，关节n上方的坐标系首先需要绕轴[Zn-1]旋转[θn]，接下来再沿轴[Zn-1]平移[dn]，其次再通过沿轴[xn]平移[an]，最后通过绕着轴[xn]旋转[αn]完成这两个关节坐标系之间的变换[9]。

在Zn-1轴的坐标变化可以被描述为式（1）：

[Tn-1n0=cosθn-sinθn00sinθncosθn00001dn0001]                   （1）

沿xn轴的坐标变换可以被描述为式（2）：

[Tn0n=100αn0cosαn-sinαn00-sinαncosαn00001]               （2）

則完整的位姿坐标变换矩阵可以视为式（1）和式（2）两个坐标变换矩阵的叠加，如式（3）所示∶

[Tn-1n=Tn-1n0Tn0n=cosθn-sinθncosαnsinθnsinαnancosθnsinθncosθncosαn-cosθnsinαnansinθn0sinαncosαndn0001]

（3）

1.4 正运动学分析

机械手臂的正向标准运动学解就是机械手臂末端执行器的位置和姿态的求解。由上文可知，已在D-H法则中建立了参数表和连杆坐标系，并推算出相邻关节坐标系的变换矩阵。再将表1中的数据代入公式（3）即可获得姿态变换矩阵。相对于基础位置和机械手末端执行器的姿态变换矩阵可以表示如下：

[T07=T01T12T23T34T45T56T67=nxoxaxpxnyoyaypynzozazpz0001]                 （4）

式子（4）的第四列是位置向量在相对于坐标系的三维空间下的机械臂末端执行器上的参考点。

其 中 ：[nx，ny，nz，ox，oy，oz，ax，ay，az，px，py，pz]是一组和关 节 变 量[θ1，θ2，θ3，θ4，θ5，θ6，θ7]有关的函数。且在[T07]基础上建立了机械手的正运动学模型，并通过计算关节角度得到了机械手末端的姿态和位置。

2解析机械臂工作空间

在机械臂工作空间求解[10]中，手臂腕部位置的工作空间用如公式（5）表示：

[w=pxw（q1，...，q7）pyw（q1，...，q7）pzw（q1，...，q7）qmini≤qi≤qmaxi，i=1，2，...，7]               （5）

对于具有明确设计的机械手，通过广义坐标[qi]确定工作空间，并能用关节变量[θi]定义广义坐标[qi]。

2.1 机械臂机器人工具箱建模

依据建模软件得出的两种机械臂的模型对比分析图，可以直接得出：两种机械臂结构设计上的差异主要在关节1位置处和关节2位置处。

2.2蒙特卡洛法采样机械臂

蒙特卡洛法[11]是一种借助于随机抽样来进行分析数学问题的一种数值方法。该方法会把某个随机概率函数模型与需要解决问题的数学模型相结合，经过仿真计算可以获得随机解，可以将得到的所有随机解近似地认为是所需解决数学问题的全部解[11]。如下所示步骤为利用蒙特卡洛法来求解七自由度手臂构型的工作空间，分为四步：

1）机器人正向运动学模型被求解，确定了机器人末端参考点在坐标系中的位置方程。

2）在关节变量范围内，利用Rand函数随机求取关节变量值。

3）在运动学方程中，将步骤2中的关节变量替换为末端参考点的空间位置。

4）在三维图中表示出末端参考点，形成机械臂工作空间云图。

3 工作空间性能指标

本文采用两种指标来评估比较机械臂的性能指标，分别是机械臂在单位长度的空间体积以及SLI指标。一般情况下，在相同长度的条件下，机械手的工作空间体积会随着其设计的不同而变化。机械手的长度变化，工作空间也会随之变化。所以，在初期设计机械手的时候就应该采用最优构型，做到相同长度条件下，其所能达到的工作空间体积最大，避免后续的修改以及弃用，造成不必要的资源浪费。SLI是用来衡量机械臂柔性的数据指标，其公式（6） （7）如下所示，定义为：机械手连杆长度与臂端空间可达体积立方根的比值[12]。

[QL=LV3]                                     （6）

[L=i=1n（ai+di）]                                       （7）

式子（6）中[ai]和[di]分别为连杆长度以及连杆偏置量; V是机械手的工作空间体积;L是机械手连杆总长度。一般来说，机械手的设计会随着[QL]的数目减小而变优。

由于机械手的长度直接决定了串联机械手的工作空间，因此不能仅仅以机械手的工作空间作为衡量机械手性能的指标。本文采用机械臂在单位长度上工作空间体积作为评价机械臂工作空间大小的分析指标，即：

[E3=vi=1nli]                                            （8）

其中，n 表示机械臂连杆的数目，[li]表示机械臂第 i 个连杆的长度。

4 手臂构型3D工作空间对比分析及仿真

4.1基于仿真软件的工作空间仿真与分析

新增剖切视图的分析与研究是很有必要的，因为对于机械臂的工作空间凡是通过蒙特卡洛法生成的只能进行针对机械手工作性能的初步判断。此外，在以往的研究分析中，大部分工作性能分析都是通过三维模型图的外部表面进行分析。但是内部仍然存在着空腔以及空洞，所以无法完全判断其完整的工作性能。

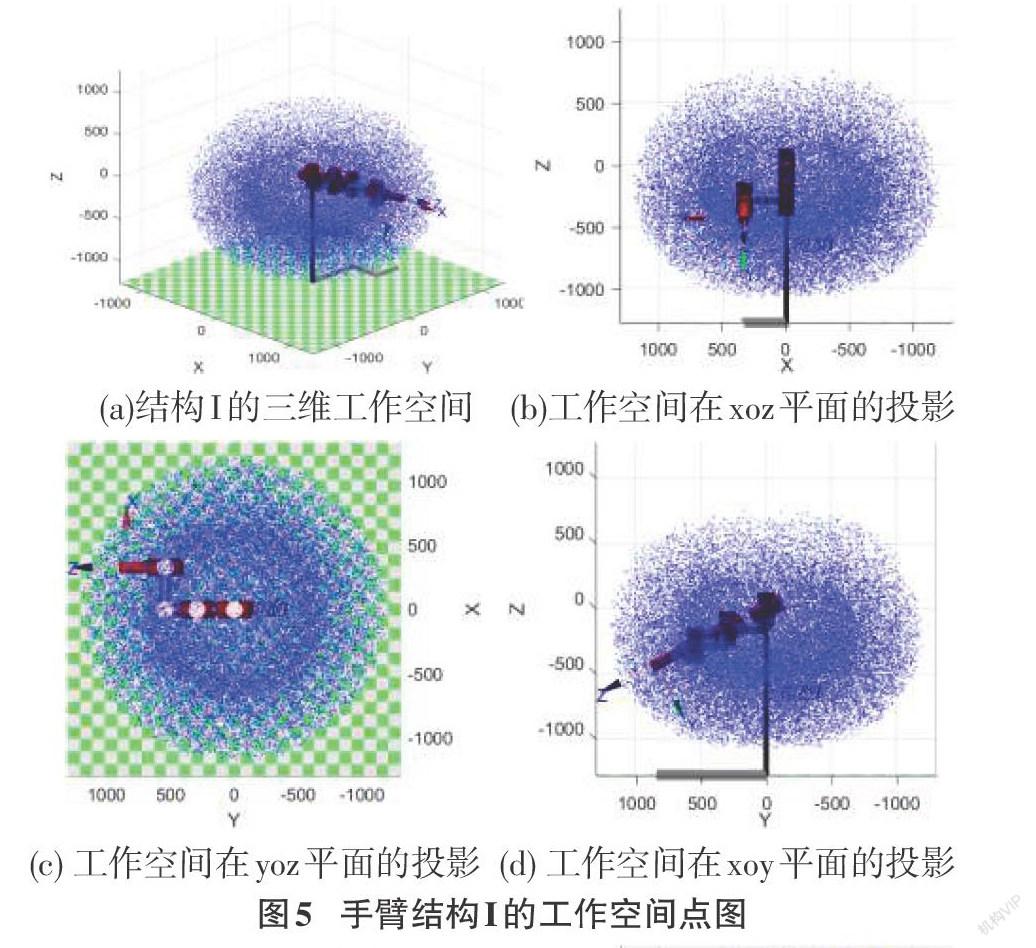
本文通过使用随机函数序列，在仿真软件中取随机数N=400000，得到七自由度机械臂工作空间。

之后在三维软件中绘制其截面图如图7和图8所示，由图可得其精密工作空间体积。

4.2指标的对比分析

表3显示了两组数据的比较结果，结合式（6） （7）并且基于SLI[12]指标计算得出了两种机械臂的值，由于其手臂在设计上的特殊性，本文仅研究臂型的腕部位置，在计算L值时会忽略[d6]。

由表3可得，两种构型在长度配置相同的条件下，结构Ⅰ的工作空间体积明显小于结构Ⅱ，且从[QL]值也可得，结构Ⅰ的灵活性是差于结构Ⅱ的，此外结构Ⅱ的单位空间体积远大于结构Ⅰ，所以结构Ⅱ是较好构型。

5 结论

本文对两种相同长度但构型不同的七自由度机械手进行了运动学分析，并利用建模软件进行了仿真模拟，获得其可视化点云图，最后再通过各项指标对比分析以及三维空间剖切图得出，手臂长度相同构型差异情况下，构型Ⅱ的单位空间体积大于构型Ⅰ，并且构型Ⅱ的灵活性优于构型Ⅰ。本文主要为机械手的工作空间提供了优化分析，旨在改善机械手结构效率以及增大工作空间达到最优构型研究奠定了基础。

参考文献：

[1] 赵亞川，李庆杰，高世卿，等.一种超冗余机械臂的工作空间求解方法[J].电子机械工程，2019，35（6）：61-64.

[2] 刘彦伯.堆垛并联机器人的工作空间分析与设计[J].轻工科技，2020，36（12）：37-39.

[3] 柯江岩，林荣川.分拣机器人复杂工作空间下灵巧度控制方法[J].集美大学学报（自然科学版），2020，25（6）：461-467.

[4] 叶鹏达，尤晶晶，仇鑫，等.Stewart衍生型并联机器人的工作空间分析[J].机械设计与研究，2020，36（4）：47-51，61.

[5] 鲁凯，万小金，李清蕾，等.8-SPU并联机器人工作空间分析及参数优化[J].机床与液压，2018，46（21）：20-23，42.

[6] 崔建昆，俞佳俊，曹丽亚.3-RRR平面并联机器人全姿态工作空间及其特性研究[J].机械传动，2018，42（9）：145-148.

[7] Alebooyeh M，Urbanic R J.Neural network model for identifying workspace，forward and inverse kinematics of the 7-DOF YuMi 14000 ABB collaborative robot[J].IFAC-PapersOnLine，2019，52（10）：176-181.

[8] Milica L，N?stase A，Andrei G.A new insight into the geometric models and workspace volume of the 6RSS manipulator by disjunction of the translational and orientation subspaces[J].Mechanism and Machine Theory，2018，121：804-828.

[9] 王春，韩秋实.六自由度串联机械臂运动学及其工作空间研究[J].组合机床与自动化加工技术，2020（6）：32-36.

[10] 石磊，许明恒，邓维鑫，等.PowerCube模块化机器人工作空间计算[J].中国工程机械学报，2011，9（1）：38-42，58.

[11] 何价来，罗金良，宦朋松，等.基于蒙特卡洛法的七自由度拟人机械臂工作空间分析[J].组合机床与自动化加工技术，2015（3）：48-51.

[12] 张雷刚.模块化六自由度机械臂运动学研究及其连杆尺寸优化[D].淮南：安徽理工大学，2017.

[13] 李宪华，张雷刚，疏杨，等.六自由度模块化机械臂腕部工作空间量化对比分析[J].计算机应用研究，2017，34（9）：2666-2669.

【通联编辑：唐一东】