企业高级人才队伍时滞系统建模及其状态反馈镇定控制

薛 燕,蔡智辉,张宝琳

(1.中国计量大学 理学院,浙江 杭州 310018;2.青岛科技大学 自动化与电子工程学院,山东 青岛 266061)

在知识经济时代,现代企业处于高度不确定性、激烈的竞争环境中,管理者面临的挑战发生了巨大变化,其中知识型员工成为企业长期发展的关键要素和工作主体。知识型员工是拥有知识资本并产生经济收益的高层次专业技术人员。自从知识员工的定义提出来以后,针对企业知识员工大量流失问题,如何对企业各类员工进行招聘、解聘、转岗,进而确保企业高级人才吸收、保留和稳定等问题引起了国内外学者的持续关注[1-4]。同时,加强知识型员工的科学管理对企业高级人才队伍的长期发展也非常重要。文献[5]分析了企业高级人才队伍的变化及其管理对企业组织绩效的影响;文献[6]通过人才心理契约因果模型建构和分析,说明了知识型员工和管理者之间的关系状态——心理契约对员工是否释放创造力的影响;文献[7]通过对企业技术创新因素的分析,强调了技术创新对企业管理的重要意义;文献[8]研究表明了管理者的企业家导向,知识型员工的积极印象管理动机,专业度等因素对员工的创造力有显著的影响;文献[9]通过分析知识型员工在管理过程中存在的问题,提出了具体的解决措施,为企业实现长久稳定的发展提供了借鉴;文献[10]通过分析高科技知识型企业中90后新生代员工的特点,提出了对应的激励政策,为广大企业的内部协调管理提供参考价值。上述文献都是从不同的角度分析了知识型员工及其管理对企业高级人才队伍系统稳定及其企业绩效的重要性。事实上,企业知识型员工系统在人力资源管理过程中存在诸多时变不确定性因素,例如人才流失、自然退出或意外性质等,上述因素往往导致知识型员工队伍不稳定,给企业带来不可避免的资产流失、人才成本剧增等影响。同时,考虑企业岗位运作的实际情形,企业在招聘(或解聘)员工时,在经过一段时间的实习期(或末位考察期)后,知识型员工才能达到岗位的胜任需求。因此,招聘(或解聘)决策行为具有时滞性质,分析并研究含招聘(或解聘)滞后的高科技企业知识型员工系统的动态稳定问题对于人力资源管理具有重要意义。

近年来,学者们从系统控制的角度开始研究企业高级人才队伍的动力学模型及其控制问题。文献[11]基于控制论方法建立了知识型员工流动的动态模型,提出了优化控制的科学管理策略;文献[12]基于鲁棒控制方法定量地研究了企业人才动态稳定的决策问题;文献[13]采用鲁棒优化法分析了含不确定项的人力资源系统模型,对企业制定人员实际流动策略具有一定作用;文献[14]研究了企业人才队伍系统的最优保性能控制策略,为高科技企业制定知识员工人力资源管理策略提供了依据;文献[15]考虑了知识型员工的不确定性并基于鲁棒控制理论,给出了最优保性能决策方法;文献[16]基于滑模控制方法研究了服务型企业员工动态系统模型,仿真结果表明了该方法可以使系统在有限时间渐近稳定。容易看到,针对企业高级人才队伍系统的动态稳定问题,目前考虑企业员工招聘或解聘滞后情形的研究并不多见。另一方面,注意到企业人才队伍员工内部转岗率、自然离职率和主动离职率的时变摄动值通常为不确定的甚至随机的,该摄动值往往会给企业员工数量的动态稳定乃至企业的短期效益和长期发展带来不利影响。因此,研究企业员工动态系统的建模、优化和控制问题,考虑员工内部转岗率和离职率的时变摄动特性至关重要。

本文结合现代控制理论思想,研究含招聘时滞的企业高级人才队伍的动力学建模及其动态稳定问题。首先,考虑企业高级人才队伍各类员工的转岗、招聘、解聘及其时滞因素,研究企业人才队伍系统的时滞不确定模型。其次,基于Lyapunov-Krasovskii稳定性理论,研究企业高级人才队伍系统的状态反馈镇定控制问题,得到了企业高级人才队伍系统时滞依赖稳定性条件,得到了系统的状态反馈控制器设计方法。仿真结果说明即使企业人才队伍系统存在招聘或解聘时滞以及参数不确定等情形,本文设计的状态反馈控制器可以保证企业高级人才队伍系统鲁棒稳定。

1 问题描述

由于知识型员工的知识面和知识量掌握程度不一,各个岗位对不同程度知识需求不一。因此,需要对其进行分类,以利于岗位的安排和企业的管理。基于知识型企业员工的特点[17],企业的知识型员工通常可以分为四类:管理类知识型员工、技术类知识型员工、营销类知识型员工和服务类知识型员工。企业知识型员工人力资本流动受到诸多因素的影响,本文所考虑的因素主要包括员工的离职、内部转岗、招聘和解聘等。离职包括主动离职和被动离职,内部转岗是指企业内某类员工转换为另一类员工的比率,招聘是指企业通过制定招聘策略,从企业外部引进的相关知识型人才。企业通过制定合适的招聘(或解聘)策略,对企业实行战略性人力资源管理有重要意义。

加强现代服务型企业知识员工动态管理是保持其在服务型行业竞争优势的基础。因此,建立优良的知识员工动态模型是分析企业员工系统稳定的前提。为给出企业高级人才队伍系统的一般模型,下文讨论中,不再特别强调管理类、技术类、营销类和服务类知识型员工,而是用第i类员工来刻画。

假设企业中有n(n≥1)类员工,为刻画企业中不同类型员工数量的动态演变规律,用变量xi(t)表示企业第i类员工t时刻的数量,其中,xi(t)<0表示企业第i类员工t时刻的数量少于该时刻的期望数量,需制定招聘计划增加相应人数;xi(t)=0表示企业第i类员工t时刻的数量等于该时刻的期望数量,企业不需招聘也不需要解聘该类员工;xi(t)>0表示企业第i类员工t时刻的数量大于该时刻的期望数量,企业需要制定适当策略进行员工裁员。变量θij(t)表示企业在t时刻不同类型员工的时变转岗率或离职率,0≤θij(t)≤1,i=0,1,…,n,j=1,2,…,n。特别地,当i≠j且i,j=1,2,…,n时,θij(t)表示t时刻第j类员工转化为第i类员工的时变转岗率;当i=1,2,…,n时,θii(t)表示第i类员工因离休、退休等离职相关的时变自然离职率,θ0i(t)表示第i类员工的时变主动离职率,pi(t)表示第i类员工的内部提拨率。同时,为保证企业活力和实现企业既定效益,企业必须根据发展规划进行有序、科学的员工招聘和解聘工作;下面用ui(t)表示第i类员工t时刻应该招聘或解聘的数量,ui(t)≥0时表示员工数量不足,应该招聘,ui(t)<0时表示员工数量盈余,应该以适当方式进行解聘。已经注意到,企业在实际招聘过程中,由于种种原因,导致t时刻招聘的员工没能按时入职,也就是说,企业的招聘通常存在时滞现象,该时滞往往会影响企业员工系统的稳定性。综上所述,考虑企业中各类员工的内部转岗、离职以及员工招聘/解聘及其招聘/解聘过程中的时滞等因素,企业员工动态系统可以描述为

(1)

其中,h≥0为招聘时滞,

(2)

令

(3)

将式(3)代入(2),bij(t)可进一步表示为

bij(t)=

(4)

于是,将式(4)代入(1)可得

(5)

其中:

(6)

(7)

注1:与文献[14]中不同的是,本文的企业员工系统动态建模过程中,对员工招聘和解聘数量没有采用不同的变量分别进行表示,而是引入了统一的变量ui(t)表示第i类员工招聘或解聘的数量,并通过其取值为非负数和负数分别表示应该招聘和解聘的数量。

定义如下变量:

(8)

则由(5)式可得企业员工系统状态空间方程为

(9)

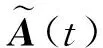
A=

(10)

(11)

令

(12)

于是,企业员工系统(9)可改写为

(13)

其中,u(t)=0,t∈[-h,0]。

由(13)知,对于不确定项f(x(t)),必存在常数ε>0,使得

(14)

本文将招聘或解聘量ui(t)视为控制分量,将各类员工数量xi(t)视为状态分量,建立了含招聘时滞的企业员工系统动态模型,其目的在于利用现代控制理论和方法,从系统控制的角度定量研究企业在每个招聘周期应该进行招聘还是解聘工作,以及招聘或解聘多少员工来保持企业员工队伍系统稳定的方法,特别是,分析时滞企业员工系统保持渐近稳定的条件,研究使得企业员工系统渐近稳定的最大招聘时滞,实现对企业人力资源管理的辅助决策和优化。

为得到本文的主要结论,先给出一个引理。

引理1[18]设x(t)∈Rn为具有一阶连续可微的向量值函数,对任意X,M1,M2∈Rn×n,Z∈R2n×2n,和函数h:=h(t)≥0,下面积分不等式成立:

(15)

其中,

(16)

2 稳定性分析

设计状态反馈控制律:

u(t)=Kx(t),

(17)

其中,K为待求的n×n增益矩阵。

将式(17)代入(13)得闭环系统

(18)

定理1给出了闭环系统(18)渐近稳定的一个充分条件。

定理1对给定的ε>0和h>0,企业员工闭环系统(18)渐近稳定,如果存在n×n矩阵P>0,R>0,n×n矩阵X1,X2,n×n矩阵Y1≥0,Y2,Y3≥0和n×n矩阵K使得下面不等式成立:

(19)

(20)

其中,

(21)

证明:构造Lyapunov-Krasovskii泛函

(22)

其中,xt=x(t+τ),τ∈[-h,0],P和R为代求的对称正定矩阵。

式(22)沿系统(18)关于时间t求导数,得

其中,

Δ1=xT(t)(ATP+PA)x(t)+
2xT(t)PKx(t-h)+
2xT(t)Pf(x(t)),

(23)

(24)

由式(14)及式(23)得到

Δ1≤xT(t)(ATP+PA+ε2I)x(t)+
2xT(t)PKx(t-h)+

2xT(t)Pf(x(t))-fT(x(t))f(x(t))。

(25)

根据引理1,知任意满足式(20)的n×n矩阵X1,X2,n×n矩阵Y1≥0,Y2和Y3≥0,我们有

(26)

其中,

进而,由式(24)和式(26)得

Δ2≤βT(t)(hΓTRΓ+Ω1+hΩ2)β(t)。

(27)

其中,

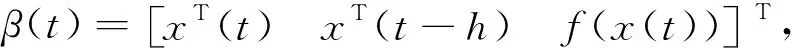
进一步,我们有

(28)

其中,

(29)

根据Lyapunov-Krasovskii稳定性理论,若矩阵不等式Λ<0成立,则由式(28)知闭环系统(18)渐近稳定。事实上,根据Schur补引理,Λ<0成立当且仅当矩阵不等式(19)成立。定理证毕。

为求解控制增益矩阵K,矩阵不等式(19)的左边分别左乘和右乘对角块矩阵Π1及其转置矩阵,不等式(20)的左边分别左乘和右乘对角块矩阵Π2,其中

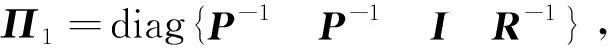
并令

(30)

(31)

其中,

(32)

特别地,当时滞h=0时,在状态反馈控制律(17)作用下,得闭环系统

(33)

为保证闭环系统(33)渐近稳定,增益矩阵K可通过求解下面线性矩阵不等式得到

(34)

3 数值仿真

为说明本文方法的有效性,我们下面分析含有招聘或解聘时滞的某企业高级人才队伍系统。设该知识型员工系统由技术类、管理类、营销类和其他类知识型员工构成,分别对应系统描述中i=1,2,3和4的情形。各类型知识型员工的内部提拔率、自然离职率、主动离职率、岗位转岗率等由表1和表2给出[16]。

表1 企业各类员工的内部提拔率pi、主动离职率c0i 和自然离职率cii

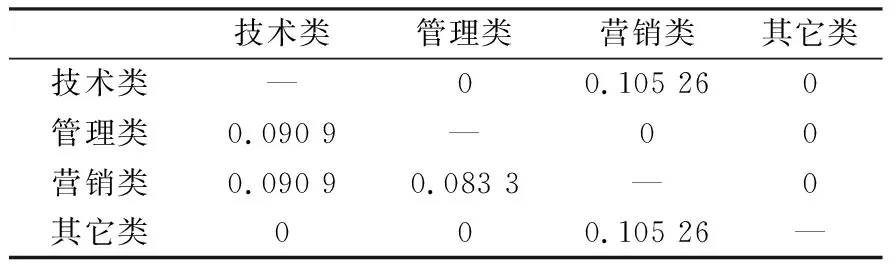
表2 企业各类员工的内部转岗率cij(i≠j)

由表1和2可得企业员工系统矩阵为

A=

设系统初始状态为

K0=

K1=

K2=

K3=

当与上述不同控制增益对应的控制器(亦即招聘策略)作用在企业员工系统时,企业4类员工在招聘策略下的数量变化曲线由分别由图1～4给出,对应地,四类员工在不同招聘周期应该招聘或解聘的数量分别由图5～8给出。

由图5～8可以看出:一方面,时滞越大,各类员工达到稳定状态的周期越长,即企业高级人才队伍系统渐近稳定的时间越长;另一方面,即使存在时滞,人才队伍系统仍然能够保持渐近稳定,说明本文设计的招聘策略是有效的。

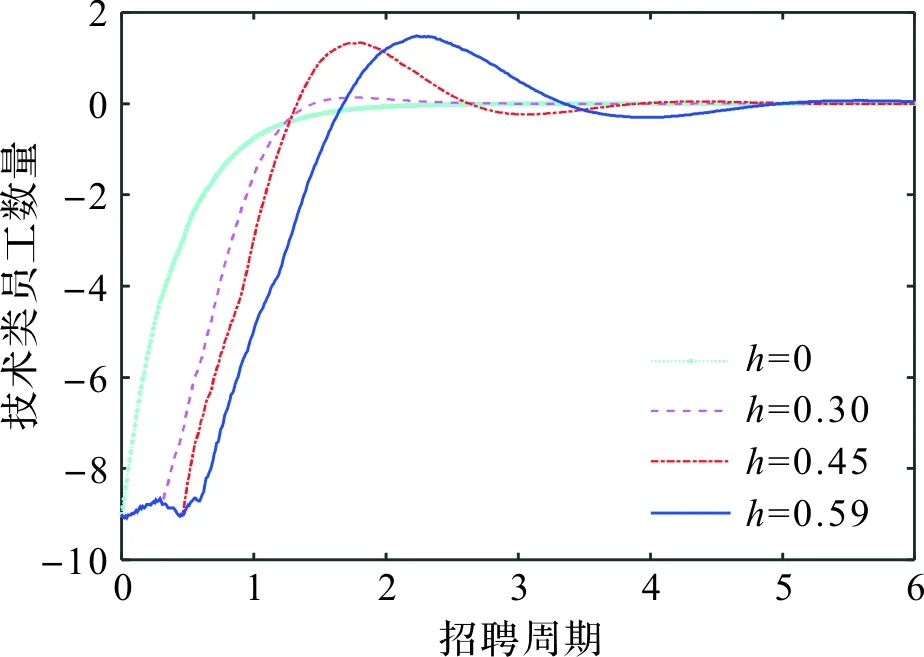
图1 技术类员工数量Figure 1 Number of technical employees

图2 管理类员工数量Figure 2 Number of management employees

图3 营销类员工数量Figure 3 Number of marketing employees

图4 其它类员工数量Figure 4 Number of other employees

图5 技术类员工招聘数量Figure 5 Number of technical staff recruitment

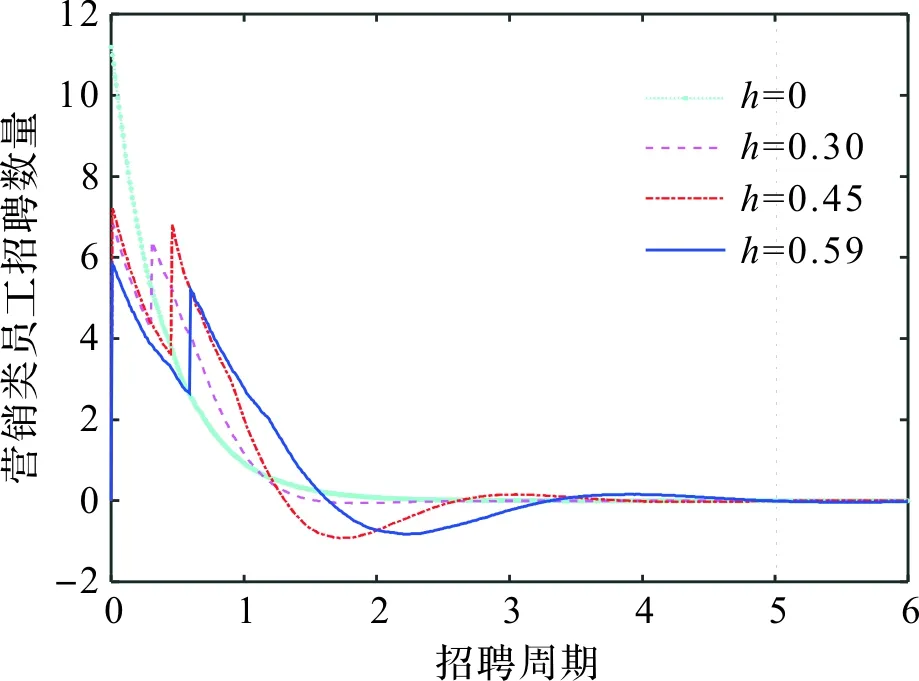
图6 管理类员工招聘数量Figure 6 Number of management staff recruitment

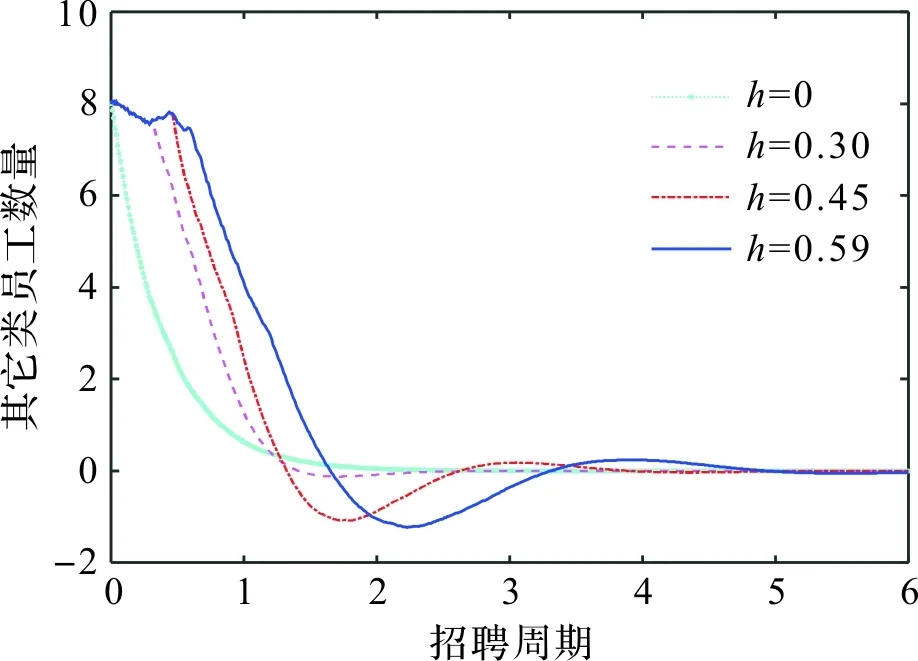
图7 营销类员工招聘数量Figure 7 Number of marketing staff recruitment

图8 其它类员工招聘数量Figure 8 Number of other types of staff recruitment

4 结 论

本文研究了含招聘滞后的企业高级人才队伍建模及其状态反馈镇定控制问题,考虑了各类员工转岗、招聘行为及其招聘时滞等因素,建立了企业高级人才队伍的不确定时滞动力学模型。进而基于时滞系统的Lyapunov-Krasovskii稳定性理论,得到了企业员工闭环系统渐近稳定的时滞依赖条件,并设计了系统的状态反馈控制器。仿真结果表明,本文设计的状态反馈控制器可以保证企业高级人才队伍系统渐近稳定。