静叶安放角变化规律对螺旋轴流混输泵流动特性的影响

马希金，韩作鹏，宛 航，张立传

（兰州理工大学 能源与动力工程学院，兰州 730050）

0 引言

随着大量海上油田被发现，如何高效经济地对石油开采已成为目前热门话题［1］。实际原油开采过程中，原油常常与化石燃料气体相伴，若仅凭地壳压力或人力等因素势必导致开采成本高和收益低的局面，这有悖于国家能源开采战略，因此必须借助增压装置——泵为原油增压以提高产率［2］。近年来，海上石油开采平台对气液两相混输泵的性能需求日益增加，故高性能油气混输泵越来越引起工程单位重视，气液两相混输泵也因其高效的工作方式和经济效益成为了研究热点［3］。

相较于单相泵而言，混输泵的内流机理更为复杂，为了获取最优的泵性能，通常对混输泵的结构进行优化来增强液相对气体的夹带作用，从而抑制输送两相流过程中的气液分离［4］。混输泵的增压单元由动叶与静叶组成，虽然气液混输泵内能量转换的核心过流部件是动叶，但静叶——扩压元件亦有举足轻重的作用。混输泵中的静叶又称整流器，不仅具有传统导叶消除流体速度环量完成能量转化作用［5］，还有着特殊作用：一是压缩气体；二是再次混合气液两相介质：利用叶片的剪切作用破碎由动叶转动形成的气液分离和滞留气团，即调整气液两相的流动状态，保证下一增压单元中两相介质的输送［6，7］。因此，其结构的优劣直接影响到混输泵性能及稳定性。吴志旺等［8］分析了冲角对泵抗空化性能及外特性的影响。余志毅等［9］通过对叶片的负载和进出口安放角的研究获得了轴流泵安放角沿轴面流线的变化趋势。张人会等［10］将ANSYS软件与Matlab软件相结合揭示了空间导叶在消除旋转环量及能量转化过程中的工作原理，得出了不同包角下其动能、压能及速度矩的变化规律。潘中永等［11］基于滑移网格理论分析了安放角成双圆弧、线性和单圆弧变化规律对离心泵性能影响，并发现单圆弧变化规律对离心泵水力性能影响大于双圆弧和线性对离心泵水力性能影响。王桃等［12］分析了不同叶片安放角变化规律对前弯叶片液力透平叶轮水力性能的影响，并发现叶片安放角呈线性分布时的水力性能优于安放角呈“S”分布的水力性能，余志毅等［13］利用一元四次方程设计离心泵前置导叶并通过数值分析和实验验证该设计方法的可行性。但关于静叶安放角变化规律对混输泵性能影响的研究很少。

本文为了研究安放角从静叶进口边至出口边变化规律对螺旋轴流混输泵水力性能的影响。首先，通过设计工况确定静叶进、出口安放角。其次，基于Matlab获得不同静叶安放角变化规律所对应的静叶型线方程，并用Pro/E 5.0实现静叶翼型三维建模。最后，基于Fluent16.2分别对各个增压单元进行数值模拟并对结果进行分析：分析不同叶片安放角变化规律对混输泵外特性影响、静叶内能量损失和静叶叶片的压力负载的影响。

1 模型的建立

本文以自主研制的混输泵为研究对象，基本参数如下：设计流量Q=100 m3/h，扬程H=25 m，转速n=2 950 r/min，基于叶片无限多、无限薄假设，通过不同的叶片安放角沿轴面流线的分布规律得到不同的叶片型线曲线，以791翼型变化规律［14］对不同静叶的型线进行背面加厚完成静叶的二维设计，并基于Pro/E 5.0完成静叶的三维造型设计。

1.1 静叶型线的建立

由于静叶主要作用是消除流体在动叶出口旋转环量，所以满足设计流量下的速度三角形［14］，故进口安放角计算及结果见表1。

表1 进口安放角计算及结果Tab.1 Calculation and results of the inlet installation angle

β1为静叶进口安放角，β'为叶片进口液流角，Δα为叶片冲角，U为轮缘处的圆周速度，Vm为进口绝对速度沿轴向方向的分量，Vu为进口绝对速度。沿圆周方向的分设计时，为了减小由流体撞击产生的能量损失，因此出口安放角为90°，叶片进口边轮毂到轮缘安放角设计需满足速度环量修正方程［14］：

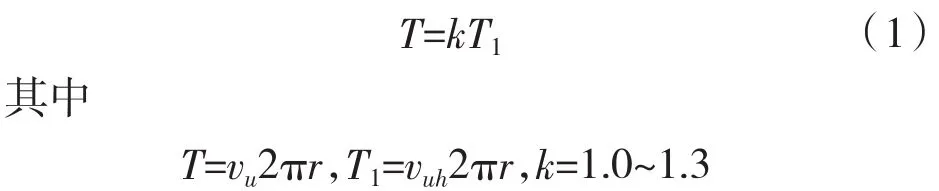
式中 vu——绝对速度的周向分量；

vuh——静叶进口轮毂绝对速度周向分量。

本文基于圆柱无关性假设和叶栅理论，将叶栅展开图中的流线近似为翼型型线，各流面内满足微分方程1，并进行驻点积分得到流体质点在流道内的流线［15］。

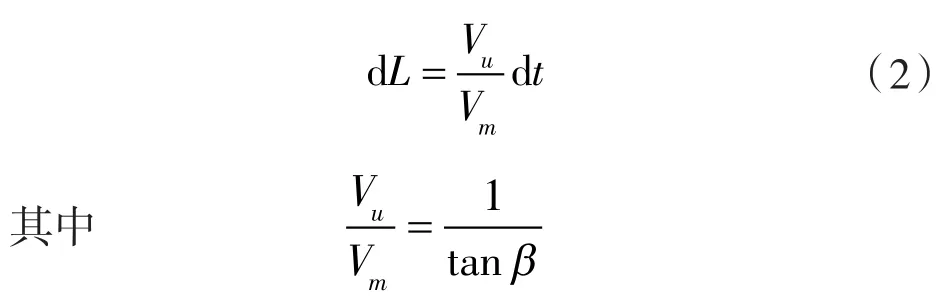
式中 L——叶栅周向长度；

t——叶片轴面流向相对长度，范围为0～1。

因此，β 变化规律决定叶栅内翼型的形状。

本文研究的静叶型线安放角沿轴线变化规律分呈线性变化和呈非线性变化两种。当安放角沿轴面流线变化规律呈线性分布时，满足方程（3）；当安放角沿轴面流线变化规律呈非线性分布时，满足方程（4）［16］：

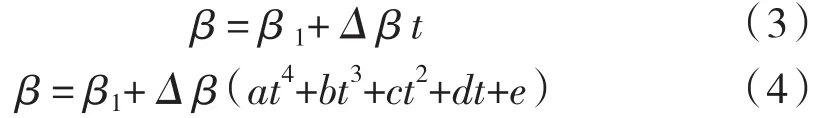
式中 β——叶片安放角；

β1——静叶进口安放角；

Δ β = β2- β1，其中β2为静叶出口安放角。

当安放角呈非线性变化时 a，b，c，d，e［17］满足条件：βt=0= β1；βt=1= β2；；βt=m= β1+ Δ β n；因 5个方程线性无关，即存在唯一的解，因此，当m和n取不同值时就可得到不同的型线方程。

为确保安放角呈非线性变化所确定的静叶型线形状良好需符合以下要求：（1）型线的曲率半径方向在同一侧，即最小安放角不得小于16.3°。（2）在安放角按不同变化趋式确定翼型时，必须保证最大安放角不超多90°。经多次实验给定以下约束：

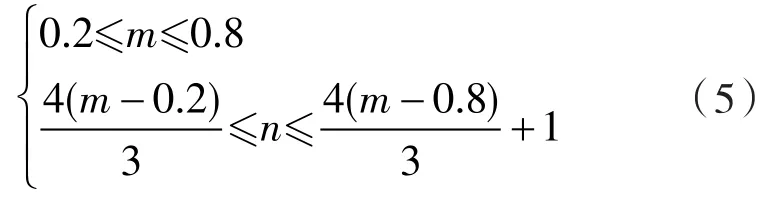
叶片安放角呈非线性时，m和n取值见表2，并采用逐点积分法确定型线。

表2 参数m和n的计算及结果Tab.2 Calculation and results of parameter m and n

最终确定5种静叶型线安放角变化规律，如图1所示：其中M0为线性变化，其余为非线性变化。为提高计算精度，将其进、出口适当延伸，如图2所示。

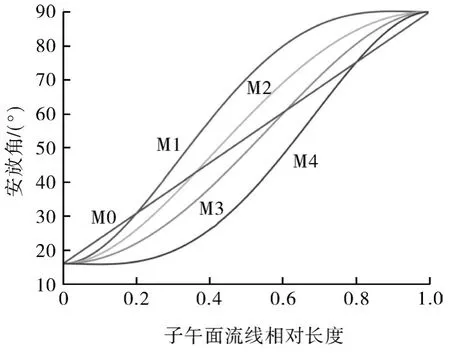
图1 安放角沿轴线分布规律Fig.1 Distribution law of installation angle along axis

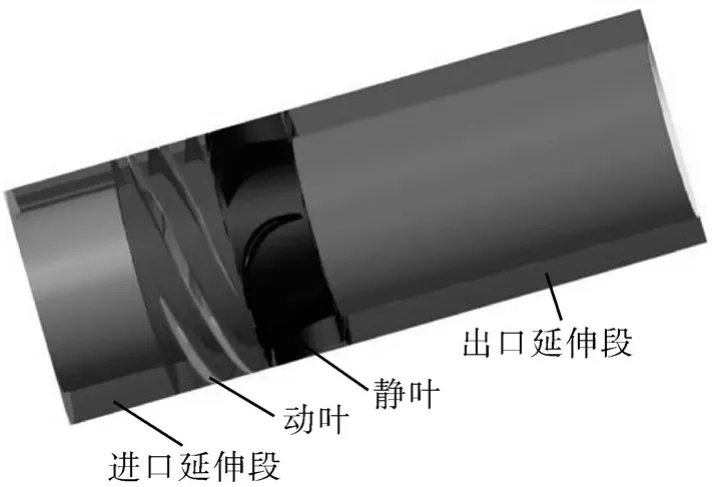
图2 三维结构Fig.2 Three-dimensional structure diagram

1.2 数值模拟

1.2.1 多相流模型

本文采用Mixture多相流混合模型，为简化模型，其中液体（水）主相，副相（气体）为理想不可压缩气体。并假设进口为均匀的泡状流且满足连续性方程和动量方程，气液两相流的基本控制方程如下［18］：

连续性方程：

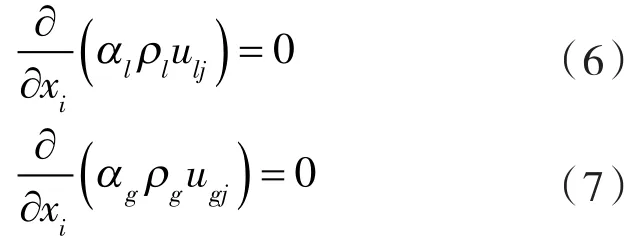
动量方程：

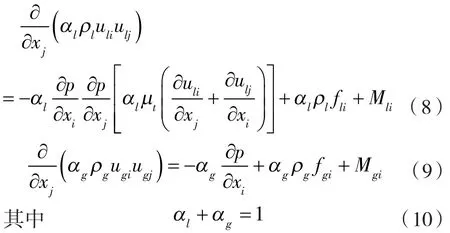
式中 αl，αg——液相、气相体积分数；

ρl，ρg——液相、气相密度；

μt——动力黏度；

p——压力；

ul，ug——液相、气相速度；

f——质量力；

Ml，Mg——液相、气相表面张力。

1.2.2 网格无关性检查

对整个计算域进行非结构化网格划分并对叶片边缘处进行局部加密如图3所示，网格无关性检查结果如图4所示。当网格数≥1 979 052时，增压能力和效率变化小于0.01%，因此网格数已不是影响混输泵主要因素，故最终确定混输泵网格数在197万以上足以保证其计算精度。

图3 非结构化网格Fig.3 Unstructured grids

图4 网格无关性检查Fig.4 Grid independence check

1.2.3 数值方法及边界

使用有限体积法对控制方程进行离散，采用mixture混合模型和k-ε（RNG）湍流模型；采取标准壁面函数处理近壁面流动，且固壁无滑移。进口设为速度进口；出口域离回流区较远，认为是充分发展的湍流区，故设为自由出流；采用Simple-C算法耦合流体的速度压力，速度场和压力场均采用一阶迎风格式离散，松弛因子保持默认；监测残差值设为10-4。

2 结果及分析

2.1 混输泵外特性分析

2.1.1 含气率对各模型水力性能影响

将5组不同增压单元在不同进口气体体积分数工况下进行数值计算，单级压缩单元的增压能力和效率如图5所示。从图中看出，随着进口气体体积分数增加，单级压缩单元的增压能力逐渐降低，出现该现象的原因是滞留在静叶流道内的气体增加导致局部气堵和气液两相的速度滑移，使流动损失增加。

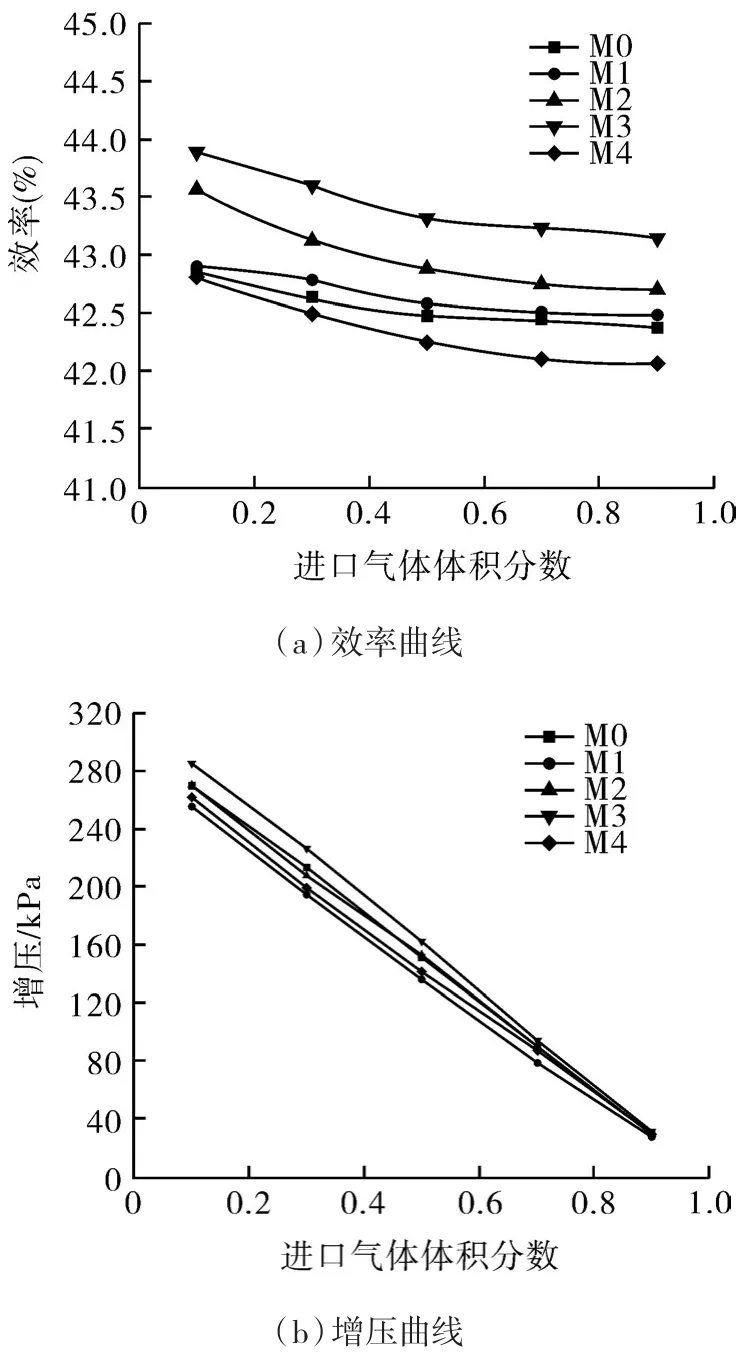
图5 不同含气率下增压变化曲线Fig.5 Pressure change curve under different GVF

提出参数λ表示不同静叶模型的流线长度，λ可由下列方程积分得到：

式中 l——轴面流线实际长度；

L——流线方程。

最终各静叶模型的实际留下长度见表3。

表3 静叶流线长度Tab.3 The streamline length of fixed blade

从图6（a）中可以看出，在相同工况下随着进口气体体积分数的增加，各模型的效率下降程度不一。在低含气率工况下，混输泵的效率下降趋势较快，在高含气率工况下的变化趋势较缓，其主要是因为气液两相在流动过程中，随着进口含气率的增加由一开始的液相夹带气相运动转化为气相夹带液相动，由于液相的物性参数远远大于气相物相数，因此混输泵静叶内能量转化能力降；但随着流道长度逐渐增加混输泵的效呈先上升下降的趋势，并且M3模型效率最高，其表明适当的增加静叶内流道长度可以提到静叶的能量转化能力，有利于效率的提升。

从图6（b）中可以看出，相同工况下M3模型的增压能力最强，M2和M0模型的增压能力相近，其中M1模型的增压能力了最差，即随着λ的增加，静叶的增压能力先增加再降低，这表明静叶内流道长度的增加有利于减少气液两相的分离程度，降低由气体增加导致气堵程度和减小气液两相间的速度滑移，使减少流动损失；M4模型的增压能力减低一方面是因为静叶流道内气液流动不稳定，另一方面是因为流线变长，叶片变厚，冲击损失增加。

2.1.2 子午流道内含气率分析

动、静叶子午流道内气体分布情况如图6所示，图中5组增压单元中动叶内的气体体积分布并没有太大区别，证明在进口含气率和进、出口角相同的前提下，由静叶产生的干涉效应对动叶流道内气体分布影响不大。

图6 子午面气体分布Fig.6 Gas volume fraction （GVF） distribution on the meridional surface

不同流量工况对模型5子午面内气体分布如图6（b）所示。对整个增压单元而言，在小流量工况下，气体聚集发生在动叶出口边轮毂处；随着进口流量的增加，气体逐渐从动叶内流出，使得静叶流道内气体含量增加，但静叶流道内气体分布较为均匀，不仅有利于降低因气液两相速度滑移产生的能量损耗，还有利于提高系统的稳定性。

2.2 能量损失

2.2.1 静叶能量损失分析

为探索流量变化对混输泵能量损失的影响，在进口含气率相同前提下，对各个增压单元在0.8 Q，0.9 Q，1.0 Q，1.1 Q和1.2 Q的5个流量工况下进行数值模拟。

根据绝对运动的伯努利方程静叶内的能量损失可用以下方程表示［18］：

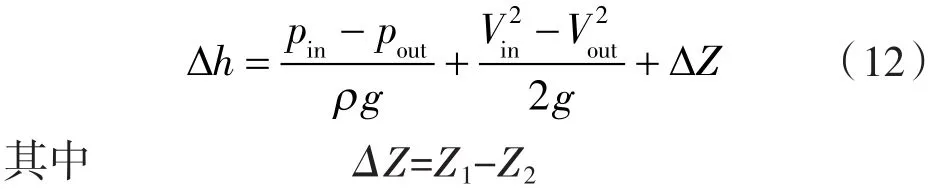
式中 pin，pout——静叶进、出口压力；

vin，vout——静叶进、出口速度；

ρ——混合密度。

该泵属于卧式结构，在含气率为0.4时，各静叶模型的能量损失结果如图7所示。从图可见，随流量的增加，5种静叶模型的能量损失均呈现出下降趋势；就非线性变化安放角而言，随着逐渐增大，能量损失先减小后增加；M3模型所确定的静叶翼型能量损失最小。

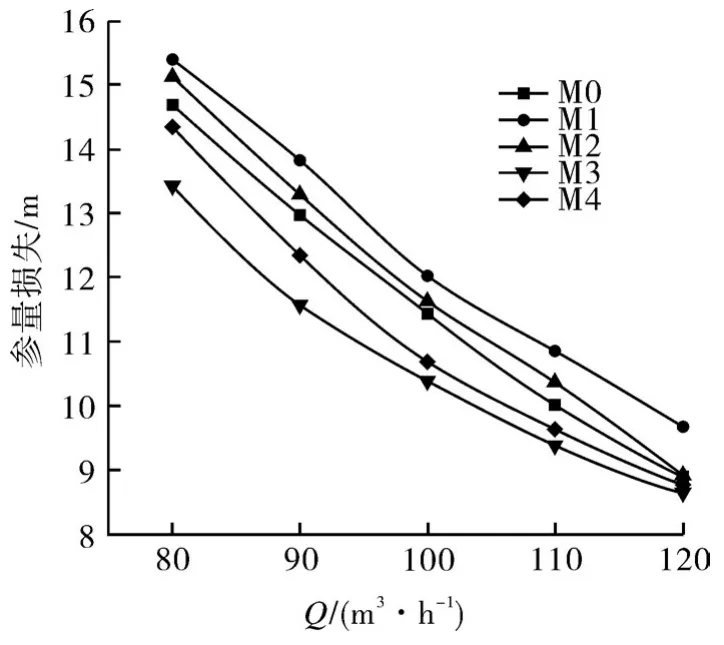
图7 不同流量工况下能量损失Fig.7 Energy loss under different flow rates

2.2.2 流场分析

图8示出进口流量是0.8 Q时的静叶子午流道内速度矢量分布，由图可知：自静叶进口边到出口边，气液两相混合流的流速逐渐降低，说明静叶流道内发生了能量的转换——流体的动能转化为压能。

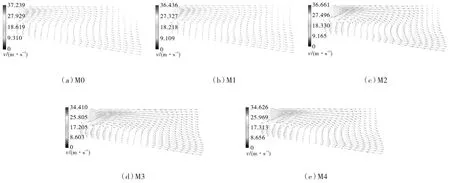
图8 不同方案子午流面速度矢量Fig.8 Velocity vector of meridional surface under different schemes

流道内能量损失主要包括静叶进口边轮毂处局部负压力梯度和气堵现象导致得压力损失，静叶流道内因气液分离和径向压力梯度导致二次流——轮缘处的流体向轮毂流动引起的能量损失，对比两者与混输泵外特性能发现，二次流是影响扬程和效率的主要原因。随着参数λ的增加，因径向压力梯度导致的二次流得以改善，能量损失减小。因此，减少轮缘到轮毂处的二次流动对混输泵的静叶能量回收具有重要意义。

2.3 压力负载分析

取0.8倍叶栅高为研究对象，得到不同流量工况下从静叶进口边到出口边叶片压力分布情况。

如图9所示：小流量工况下，从静叶进口边到出口边叶栅所受压力不稳定，随着进口流量的增加，压力趋于稳定，这是由于进口流量的增加增强了液相对气相的夹带能力，使得沿流线方向的叶片附近的气液分布更均匀；如图9（a）中安放角呈线性变化的静叶背面的压力沿流动方向变化不大，工作面的压力沿流动方向逐渐降低，且两面的压力差值逐渐减小。

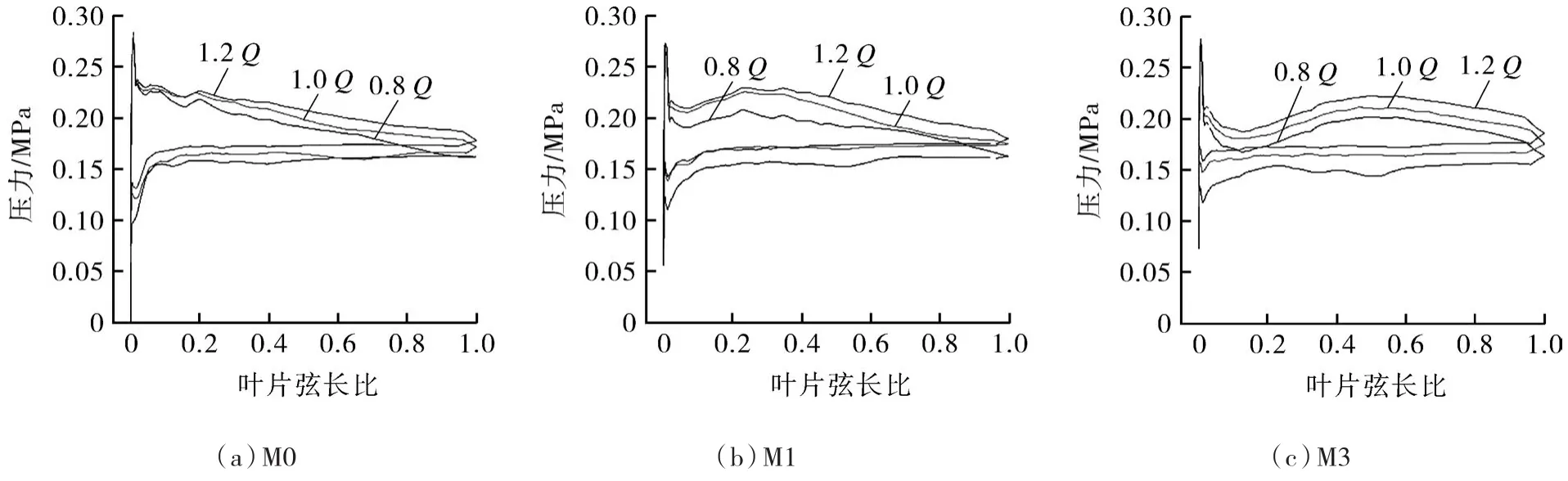
图9 静叶压力负载分布Fig.9 Distribution of pressure load of fixed blade

安放角呈非线性变化静叶如图9（b）和（c），静叶背面的压力分布较为均匀，而工作面压力分布可以分为压力骤增阶段、压力下降阶段、压力缓增阶段和压力缓慢下降阶段4个过程：由于气液混合流离开动叶时获得一定的周向速度和动静轴向间隙内气团的重新混合打破了原有的进口无冲击条件，导致气液混合物刚接触静叶进口边时冲击压力的骤增；由于沿着流体流动方向速度环量逐渐降低，所以单位面积的冲击压力逐渐下降；由于静叶翼型型线弯曲程度较大，因而沿流线方向的压力出现缓慢上升趋势，在约沿流线占比0.4的位置处工作面压力最大；当气液混合物流过弯曲程度较大的位置时，静叶工作面的压力趋于缓慢下降阶段。与M1模型相比，M3模型型线的最大曲率处更靠近出口边。

就叶片负载而言，安放角沿轴面流线性变化所确定的静叶型线更接近理想状态的压力负载分布，而安放角非线性变化规律所确定的静叶型线工作面与背面的最大压差位置更靠近叶片出水边。

3 结论

（1）在气体体积分数GVF=0.3工况下M3模型的静叶效率和静叶能量回收能力最优，相比线性变化的静叶其效率增加了1.1%；

（2）由气体分布情况看出，不同静叶叶片安放角变化规律对动叶流道内气体分布影响不大，但对静叶流道内气体分布产生明显的影响。

（3）就叶片负载而言，当静叶安放角从进口边至出口边呈线性变化时，静叶型线压力负载沿流动方向工作面和背面的压差逐渐减小；当静叶安放角从进口边至出口边呈线性变化时，叶片压差最大的位置随静叶流线长度的增加越来越靠近静叶的出口边。