钢筋混凝土柱的临界轴压比与轴压比限值

李楚舒， 李 立， 陈云波， 吴文博

(北京筑信达工程咨询有限公司， 北京 100043)

0 引言

我国《建筑抗震设计规范》(GBJ 11—89)[1](简称89年抗震规范)引入了轴压比限值概念，在工程界产生了广泛而深远的影响，无论是试验研究还是相关规范编制，无论是工程设计还是设计审查，现在都存在一种“唯轴压比”的倾向。

轴压比是一个简单而实用的工程设计参数，对于初步估算柱的断面尺寸比较方便。近些年来，工程界也在探讨轴压比限值的问题，因为工程上出现了一些难以处理的问题，比如一些高层结构的柱断面尺寸过大，由轴压比限值控制，基本上是构造配筋；而另一方面，试验结果表明，轴压比越大，柱的延性越差。因此目前工程界存在两种不同的看法：一种是要放松轴压比限值，以期得到更合理的结构设计；另一种是要严格轴压比限值，以保证抗震设计中柱具有足够的延性。

89年抗震规范只有正文没有条文说明，《建筑抗震设计规范》(GB 50011—2001)[2]6.3.7条文说明中有：“希望柱子处于大偏心受压的弯曲破坏状态，……本次修订仍以89规范的限值为依据”。笔者所能找到最早公开发表对此问题进行研究的论文是文献[3]。文献[3]从混凝土基本原理出发，将大小偏压临界点的轴压比，即临界轴压比，视为轴压比的限值；基于试验中的临界轴压比标准值，采用荷载设计值与标准值之比及材料强度设计值与标准值之比，推导出临界轴压比设计限值为1.63ξb，即0.9左右，得出了“我国现行抗震规范对抗震等级为三、四级的柱轴压比限值规定为0.9是合适的”的结论。

本文拟就钢筋混凝土柱的临界轴压比和轴压比限值这两个概念分别进行分析和讨论。

1 临界轴压比

大小偏压临界轴压比设计值为0.9的结论不符合对PM相关曲线的认识。图1是采用材料设计值绘出的不同配筋率的PM相关曲线族，类似的图形在部分教材和桥梁规范，包括欧美规范及设计手册中均有提及。从图1可以看出，矩形对称配筋的大小偏压临界点的轴压比为0.5左右。

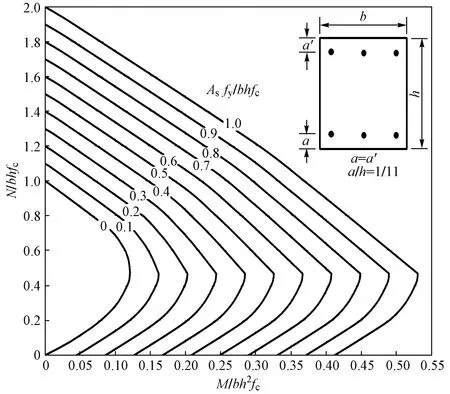
图1 不同配筋率的设计PM相关曲线族

1.1 简化推导

大小偏压临界点(平衡点)的定义为：混凝土上表面纤维压应变达到极限压应变εcu，底部钢筋拉应变达到屈服应变εy。以对称配筋钢筋混凝土矩形截面为例，截面应变分布如图2所示，截面轴力为：

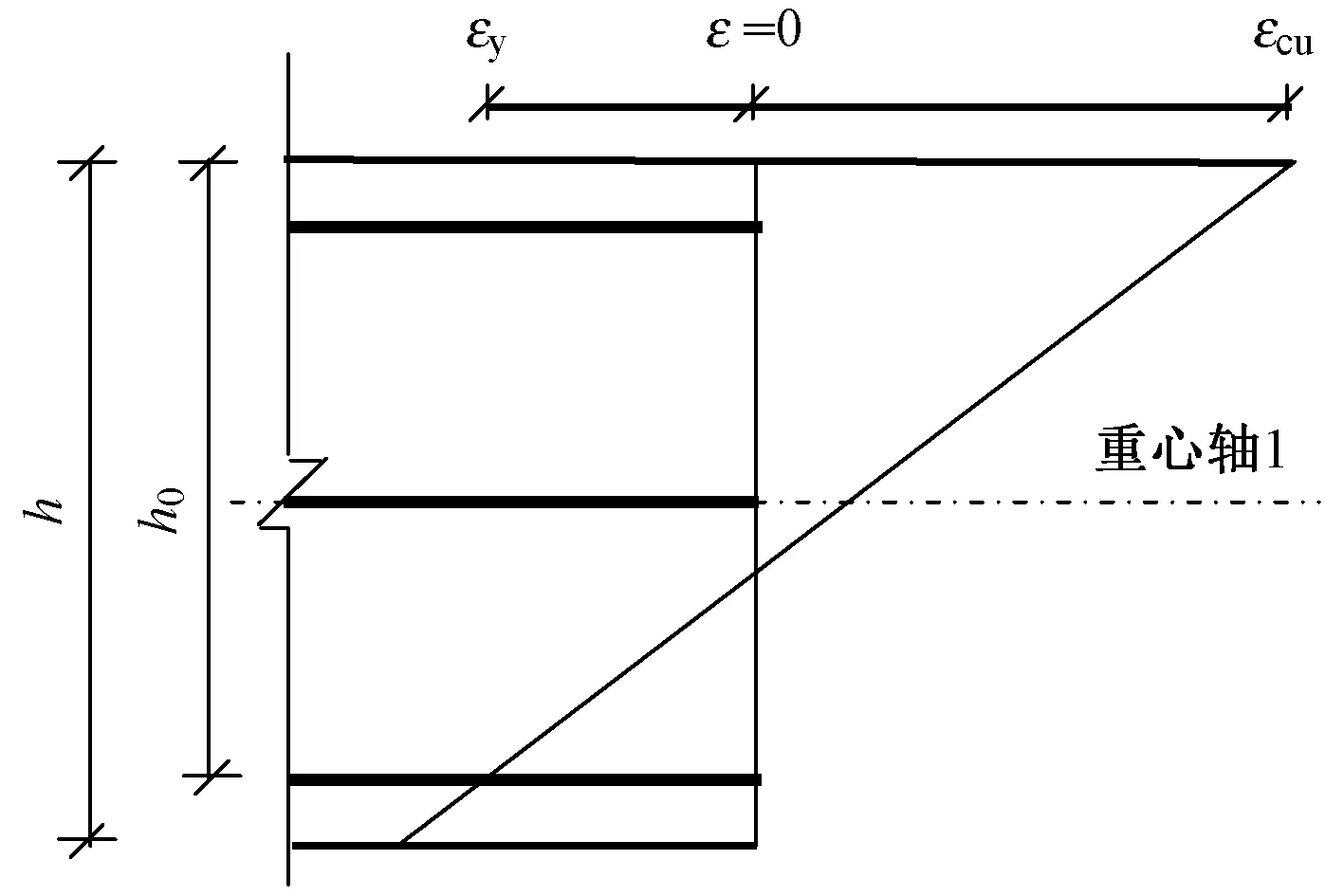
图2 大小偏压临界状态的截面应变分布图

N=Nc+∑Asiσsi

(1)

式中：Nc为混凝土压力；Asi和σsi分别为各钢筋截面面积及其应力。

假定钢筋轴力之和为零，则截面轴力为：

N=α1fcβ1xnb

(2)

根据图2的临界状态截面应变图，可以将式(2)中的混凝土实际受压区高度xn表达为混凝土极限压应变εcu、钢筋屈服应变εy与有效高度h0的关系，即：

(3)

故，临界轴压比为：

(4)

式中：混凝土等效矩形图参数α1，β1和εcu与混凝土强度等级有关(C50及以下，α1，β1为常数)；钢筋屈服应变设计值εy与钢筋等级有关；b为截面宽度；h为截面高度；fc为混凝土强度设计值。

从式(4)可以清楚地看出，矩形对称配筋的临界轴压比只与截面材料属性有关。

假定h0/h=0.9，采用强度等级在C50及以下的混凝土，强度为HRB400的钢筋(屈服应变设计值εy和标准值εyk分别为0.001 8,0.002)。

(1)采用材料标准值时，临界轴压比标准值为：

(2)采用材料设计值时，临界轴压比设计值为：

注意：本文在此问题上未考虑我国抗震设计的承载力抗震调整系数γRE。

临界轴压比的设计值与标准值之比为：

(5)

本文推导的前提假定完全同于文献[3]，但所得结论却有很大差别：1)本文得出的临界轴压比设计值为0.5左右，而文献[3]为0.9；2)本文得出的临界轴压比的设计值与标准值之比为1.0左右，而文献[3]为1.63，即荷载分项系数与材料分项系数的乘积。

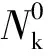
为了进一步验证本文的推导，下面给出一个具体的数值算例。

1.2 数值算例

一个简单对称配筋混凝土截面：截面尺寸为400mm×400mm，混凝土强度等级为C40，钢筋强度为HBR400，8根φ20钢筋，等间距排布，h0=360mm。采用CiSDesigner[4]软件得到的PM相关曲线如图3所示(C和Ck分别为设计值和标准值的临界点)：

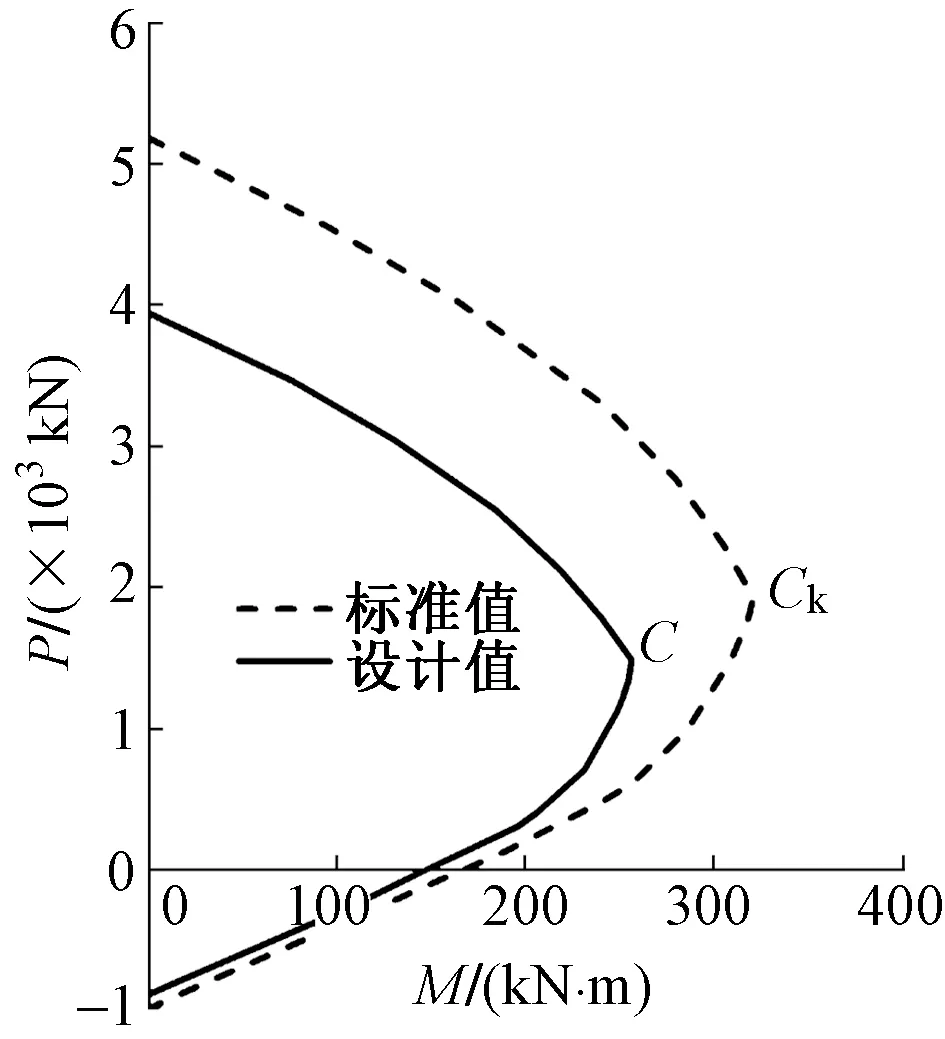
图3 CiSDesigner得到的PM相关曲线

根据材料标准值的PM相关曲线，可知临界轴压比标准值为：nk=0.45。

根据材料设计值的PM相关曲线，可知临界轴压比设计值为：n=0.48。

可以看出，数值算例的临界轴压比与1.1节中的推导结果吻合。存在的数值差异(式(4)计算的结果比数值算例略小)的主要原因是：式(4)推导时采用了钢筋合力为零的假定。如果存在腰部钢筋，当底部受拉钢筋达到屈服、混凝土达到极限压应变的时候，中性轴位于截面形心主轴之下，故钢筋的合力为压力(参见图2)。

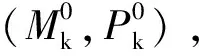
一般说来，设计轴压比对于工程设计有意义。

2 PM相关曲线

PM相关曲线是钢筋混凝土柱的核心概念之一，由混凝土和钢筋这两种不同材料组成的截面，极限承载力存在Pu与Mu的相关性。根据钢筋和混凝土的本构方程，基于平截面假定，给定混凝土受压极限应变和钢筋受拉极限应变，即破坏准则，就可以生成PM相关曲线。换言之，PM相关曲线是钢筋混凝土柱极限承载能力的包络线，荷载点位于PM相关曲线(三维就是PMM相关面)上，就说明截面达到承载力极限状态。

因为柱设计基本上写不出适合手算的一般性设计公式(原因为无法考虑所有钢筋的贡献及双偏压更是无法实现手算)，所以这个PMM相关面就是柱的基本设计依据，因此欧美规范[5-6]都没有给出正截面承载力设计的具体公式。图4给出了一条典型的PM相关曲线，C点即为临界点。

图4 典型的PM相关曲线

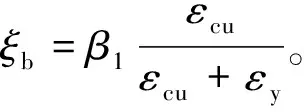
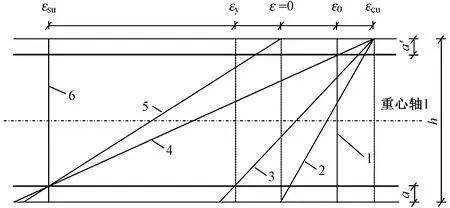
图5 CiSDesigner软件生成PM相关曲线的截面极限状态应变控制线

采用平截面假定和混凝土及钢筋的设计本构模型，可以得到任意截面和任意配筋形式的PM相关曲线。PM相关曲线是截面自身特性，与外荷载无关，所以PM相关曲线上临界点(C点)的轴压比比由式(4)得到的计算结果更具普遍意义。

3 轴压比限值

我国《建筑抗震设计规范》(GB 50011—2010)(2010年版)[7](简称10年抗规)和《混凝土结构设计规范》(GB 50010—2010)[8](简称混凝土规范)分别在6.3.6条和11.4.16条里规定柱的轴压比限值。条文说明里也都讲到这是为了保证柱的延性，而且与箍筋形式和配箍率有关。以框架柱为例，规范规定的轴压比限值在0.65～0.90之间。

从第1节中可以看出，临界轴压比设计值为0.5左右，这与规范轴压比限值相差较大。

第1节公式推导的是正截面极限承载力设计的方法，采用的是单轴(非约束)混凝土的本构关系，不能考虑箍筋约束的作用。为了考虑箍筋约束效应，需采用约束混凝土本构来分析轴压比限值的问题。

我国现有规范并未给出约束混凝土的本构模型，由于我国混凝土规范与欧洲混凝土规范EC2[5]在许多理念是相同或相似，下面采用欧洲混凝土规范EC2给出的约束混凝土本构模型做一个简化的推导。

根据欧洲混凝土规范EC2[5]的3.1.9条，当侧向约束应力σ2等于0.05倍混凝土抗压强度标准值fck时，混凝土本构(Rüsch模型)的参数可取为ε0=0.003和εcu=0.013 0。而我国混凝土规范规定的强度等级在C50以下的混凝土设计本构模型为ε0=0.002和εcu=0.003 3。这样就可以求出其对应的等效矩形应力图参数α1=0.997和β1=0.926。而我国强度等级在C50以下的混凝土设计本构的α1=0.969，规范取1.0；β1=0.824，规范取0.8。采用与1.1节相同的截面材料和参数，假定受压全截面为约束混凝土(与实际情况略有差异，但不影响主要结论)，由式(4)可以得到临界轴压比为n=0.73。可见采用约束混凝土模型，柱的临界轴压比提高了50%以上，因为混凝土极限压应变大幅提高了，幅度与配箍率有关。这个简化方法得出的临界轴压比基本处于我国10年抗规和混凝土规范规定的轴压比限值的中间值。

但是，我国10年抗规和混凝土规范将轴压比限值与抗震等级挂钩的做法值得商榷。抗震等级越高，柱配箍率要求本来就越大，从约束混凝土本构模型可以获知，其极限压应变就更大，因此理论上临界轴压比更大，而10年抗规和混凝土规范却将其轴压比限值定得更低。

显然，我国10年抗规和混凝土规范规定的柱轴压比限值不能用文献[3]的结论来进行解释。

如果采用欧洲混凝土规范EC2[5]常用的钢筋材料(εy=0.002 5)，可以得到临界轴压比n=0.70，这与欧洲抗震规范EC8[9]对中等延性DCM柱的轴压比限值为0.65比较接近。

美国设计规范[6]没有轴压比限值的相关规定。

需要指出的是，轴压比只是柱延性的一个参数，而非全部，需要进一步了解相关内容的读者可参阅扶长生所著《抗震工程学——高层混凝土结构分析与设计》[10]一书，在第4章有详细论述。简言之，柱的延性与柱的形状、纵向配筋率、轴压比等因素相关，而最大的相关因素是配箍率。新西兰混凝土设计规范NZS 3101∶2006[11]中就有相关的设计公式和图表，高轴压比采用高配箍率，以保证柱具有足够的延性。

4 结论

临界轴压比是PM曲线上的临界点(平衡点)的轴压比。矩形截面对称配筋的临界轴压比设计值为0.5左右，而非0.9；临界轴压比的设计值与标准值之比为1.0左右，而非1.63。

我国10年抗规和混凝土规范给出的轴压比限值，采用约束混凝土本构模型可以得到一定程度的验证。