贝塞尔光束的干涉本质和实现教学探讨

张明辉，李劲松

(安徽大学，安徽 合肥 230601)

早在1978年，J.Durnin[1,2]首次提出的无衍射光束概念(即贝塞尔光束)在物理学界掀起了一股科学的热潮。时至今日，贝塞尔光束不仅在非线性光学、统计物理学和原子物理学中具有重要的学术价值，而且在激光通信、激光加工和制造、激光成像、激光雷达等工程应用领域亦具有重要的应用价值[3]。然而从干涉本质而言，传统的教材和文献[4,5]对于这种光束干涉成因叙述很少。为此，本文通过对双棱镜光场的思考引入对贝塞尔光场形成物理机制的讨论，在此基础上阐述产生该光束的实验装置的物理依据，结合详细的数值模拟，对此干涉机制给出了科学的阐述。希望通过本文的探索研究为贝塞尔光束在基础物理教学方法和科学研究方面提供一定的有益参考。

1 贝塞尔光束的解

贝塞尔光束波动方程的数学表达式为

(1)

在自由空间，其具有一个形为

(2)

的解，其中

(3)

场函数为(2)描述的光场有一个违背衍射常识的性质：它在传播的过程中并不发散，“无衍射光束”就此得名。后来发现(2)的解析表达式含有贝塞尔函数，因此这种光束也被称为“贝塞尔光束”。

贝塞尔光束因迥异于其他光束的共性，而从它被发现到现在，一直受到学界和应用界的关注[6,7]，一些教材已经把它收录为教学的内容[5,8]。然而它的不发散性质背后的物理，以及产生它的实验装置的依据，在教学过程中并未详细说明。这两个问题可以通过对双棱镜光场的思考来引入，启发学生得到准确的回答，通过这一过程可以加深对内容的理解和掌握。

2 双棱镜光场的干涉解

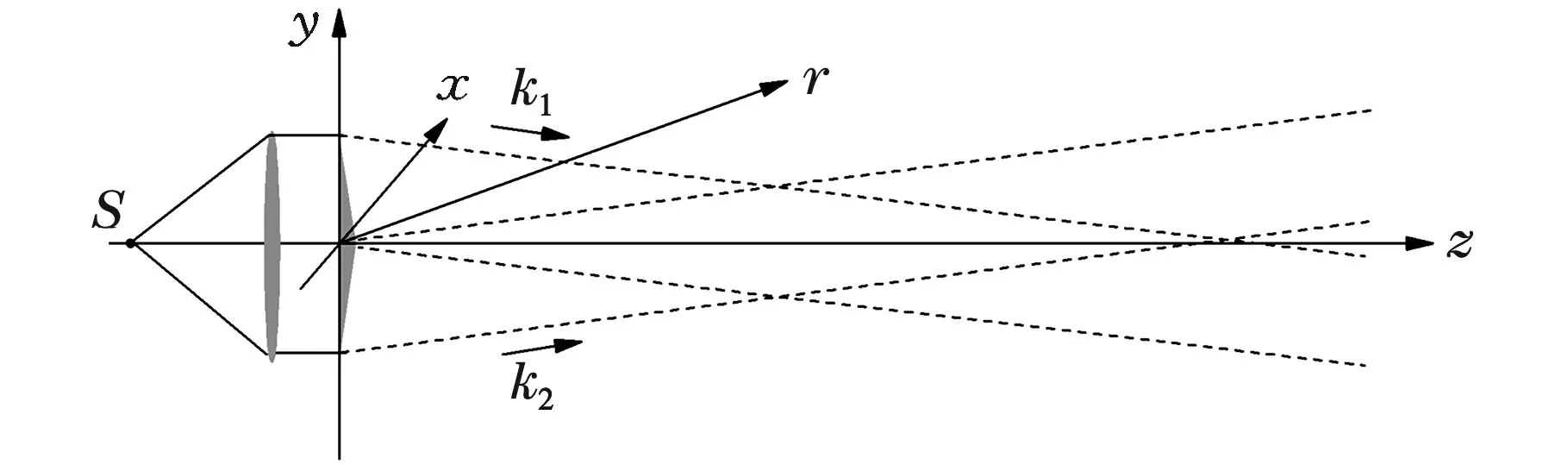
图1 双棱镜光场示意图

I(r)=|U1(r)+U2(r)|2

(4)

其中位置矢向量

r={x,y,z}

(5)

表示空间任意位置，场向量U1和U2分别代表图中两束倾斜的光场。设波矢分别为k1、k2，那么

U1(r)=exp{j(k1r-ωt)},U2(r)=exp{j(k2r-ωt)}

(6)

(6)中的

(7)

将(5)-(7)带入(4)，可得归一化光场强度为

(8)

从(8)可以看出，在图1所示的光束交叠区，光场强度是沿y方向分布的，周期为

(9)

的干涉条纹。图2为双棱镜在半空间z>0的光场的强度分布，其中(a)双棱镜光场在主平面yOz内的强度分布,(b)-(d)主平面内kz=0,10,30时的强度分布剖面图。

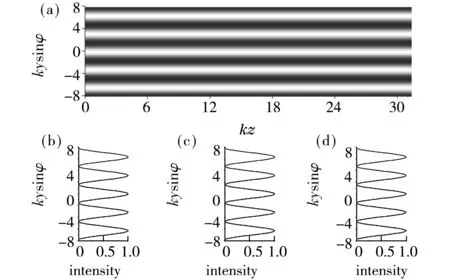
图2 (a)双棱镜光场在主平面yOz内的强度分, (b)-(d)主平面内kz=0,5,10时的强度分布剖面图

如果把图1中的双棱镜替换为相同横截面的角锥棱镜，其后光场强度将变成什么样的分布？主平面yOz内还是上述干涉条纹吗？对这个问题的思考已涉及贝塞尔光束的物理实质和实现装置的设计。

3 贝塞尔光束的物理

观察场函数(2)，一旦赋予其中的

(10)

它[(2)式]实际上是一个被积表达式为

dU(θ)=[A(θ)dθ]exp[j(kr-ωt)]

(11)

的积分，其中

(12)

(11)的复振幅部分与(6)是同构的，也就是说dU(θ)是一束振幅为[A(θ)dθ]，沿着波矢为(12)式方向传播的平面波，方位角为θ，天顶角为φ。至此，结合3对双棱镜光场的干涉理解，场函数(2)的物理图像变得清晰起来：它是具有相同天顶角角φ，在方位角θ上权重为[A(θ)dθ]的一系列平面波的干涉场。

上述物理结合思考3留下的思考，可以着手设计产生这种光束的实验装置，并用数值的方法验证这种光束的不发散性质。

4 实现贝塞尔光束的实验装置

由第4节中分析的物理可以知道，需要制备一系列具有相同天顶角φ、等权重方位角θ的平面波，并实现他们的相干叠加，叠加后的干涉场即为贝塞尔光束。第3节留下的问题已提示实现的手段——只需设计一透镜，使得透射的平行光被折射成具有上述特性的平行光簇。第3节中双棱镜的作用是把一束入射的平行光分解为两束倾斜传播的平行光，其后的重叠区即为干涉场区。受此启发，一个最容易想到的实验装置是把图1中的双棱镜替换为相同横截面的角锥棱镜，这样当一束平行光入射时，它可以分解为沿方位角0≤θ<2π方向等权重的一系列具有相同天顶角φ平面波簇，其后的半空间z>0即为平面波簇的干涉区域。

此外，还可以设计一环状的相干光源[如图3b]，把它放置在垂直于传播方向普通透镜的物方焦平面上，这样光源上位于任一θ处的点，均可视作一个点光源，它所发出的光场经透镜折射后，在像方半空间z>0形成方位角0≤θ<2π的具有相同天顶角φ=arctan(R/f)的平面波的叠加场。它的实现方式可按照图3b设计，使用平行光束照射摆放在物方焦平面上的圆环形的透光屏，透镜的像方即为所需要的干涉场。

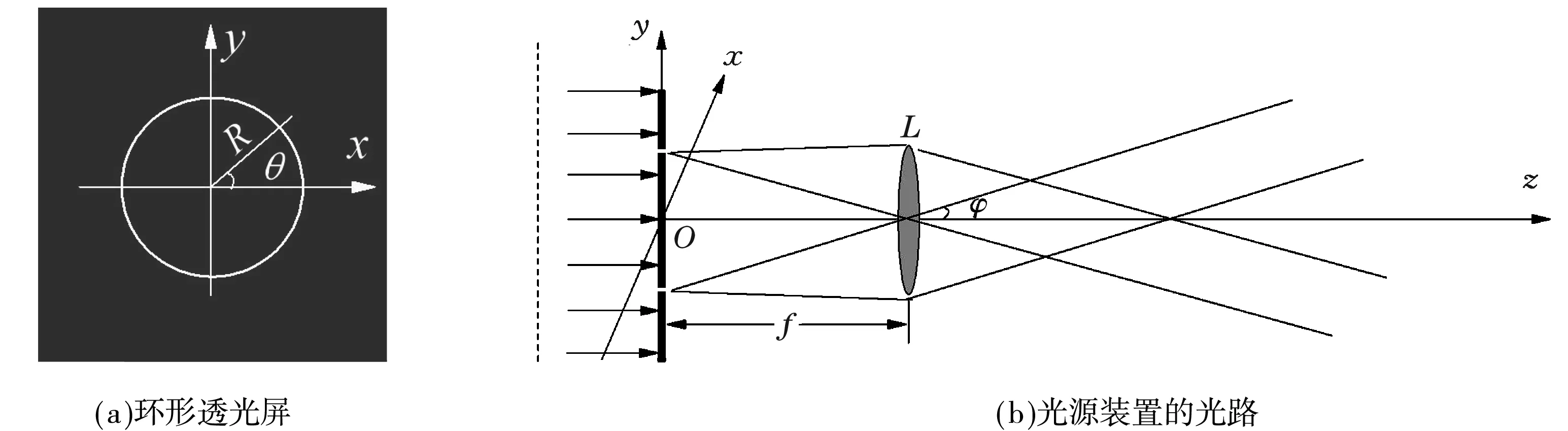
图3 产生贝塞尔光束的一种装置

5 数值验证

把(5)改写为r={ρ,z}，其中ρ=(x,y)为径向坐标，与(12)一同代入(11)，求积分得

(13)

其归一化光场强度是

(14)

可见用上述装置产生的光场，其强度I(ρ,z)只与径向坐标的模有关，而与传播距离无关。结合贝塞尔函数的性质，从(14)可以看出，如果令

(15)

其中2.408近似为贝塞尔函数J0(x)的第一个零点，得到

(16)

可视作光束的半径；如果令

(17)

π近似为塞尔函数J0(x)的第k个零点(k≥2)，得到

(18)

可视作光束的边带宽度。图4是根据(14)模拟的横截面yOx强度分布，图5(a)是光场在主平面yOz内的强度分布，(b)-(d)是主平面内kz=0,10,30时的强度分布剖面图。对照该图可以看出装置后方的束状光场确实没有发散。

图4 装置[图3]产生的光场在垂直于 z的横截面yOx内的强度分布

图5 (a)装置[图3]产生的光场在主平面yOz内的强度分布, (b)-(d)主平面内kz=0,10,30时的强度分布剖面图

7 结 论

结合无衍射光束的积分表达式，从双棱镜光场的干涉机理为出发点，引导学生理解无衍射光束由干涉实质形成的实质，同时理解产生这种光束的装置的设计原理。角锥光束是近年来学术界和应用界的研究热点[6,7]，本文的工作将有助于加强学生对这种新型光束的理解和掌握，便于他们对这一领域进行研究和跟踪，同时为基础物理教学老师在讲解该知识点时，提供一定的理论参考。