重投影优化的自由双目相机位姿估计方法

陈天择，葛宝臻，罗其俊,3

（1.天津大学 精密仪器与光电子工程学院，天津 300072；2.光电信息技术教育部重点实验室，天津 300072；3.中国民航大学 电子信息与自动化学院，天津 300300）

1 引言

自由双目立体视觉系统是通过相机旋转拍摄部分场景、分块重建并拼接三维点云的方式，实现大场景三维重建。相机位姿是指相机坐标系变换至世界坐标系的旋转矩阵和平移向量。由于双目相机自由旋转，导致左右相机的位姿不断变化，想要实现自由双目立体视觉系统的分块重建和点云拼接，就需要准确估计每个旋转位置的左右相机位姿。

旋转相机位姿估计算法主要包括旋转轴标定法和特征点自标定法。旋转轴标定法是对相机的旋转轴参数进行预先标定，结合旋转角度，计算相机旋转后的位姿。郑圣子等[1]提出一种基于多个平面标靶的旋转轴标定法，将相机光心的运动轨迹拟合为空间圆形，得到圆心即为旋转轴位置；李肖等[2]通过一个棋盘格平面标定靶，立体标定4个位置的双目相机旋转平移矩阵，利用最小二乘法求解旋转轴参数，获取双目相机的动态外参数；于海等[3]利用双线阵图像传感器对旋转角度误差进行补偿，实现高精度的角位移测量。特征点自标定法主要包括：利用图像间的多对匹配特征点和利用已知三维点与图像特征点间匹配关系两种。Sweeney、Moulon、Zhu和Zhuang等[4-7]利用两视图间的匹配特征点求解本征矩阵，通过分解本征矩阵[8]得到不同位置相机间的位姿关系，依据全局一致性同时优化所有相机在世界坐标系的位姿；杜瑞建等[9]利用单应矩阵实现高分辨率图像和双目图像的特征匹配，进而得到纹理图像与三维点云间的匹配关系；Snavely Noah、Wu C、Schonberger J L等[10-12]在已知三维点与图像特征点匹配关系的条件下，构建3D和2D点对应问题(Perspective-n-Point, PnP)，利用直接线性变换法(Direct Linear Transform, DLT)、EPnP[13]、UPnP[14]等方法求解相机位姿。还有一类方法在已知三维点的条件下，构建并优化误差函数，进而得到相机位姿的最优解。李正炜等[15]提出一种采用仿真图像进行相关度局部最优搜索的姿态估计方法；Engel J等[16]提出将相机运动前的位姿作为初值，通过最小化光度误差函数得到相机当前位姿，在相机运动连续且平滑时取得良好的效果，张可等[17]指出光流对噪声、阴影、遮挡等环境干扰因素抵抗性较差；Li等[18]提出将当前位置之前的多幅图像中的特征点云重投影回当前图像，保证有足够的特征点用来优化相机位姿；Cui等[19]提出适用于运动恢复结构(Structure from Motion,SfM)的位姿获取方法，将利用P3P方法得到的相机位姿作为初值，通过最小化特征点的重投影误差函数，得到优化后的相机位姿；周单等[20]提出基于自适应重投影误差单目位姿优化算法，以位姿初值为中心设置约束区间，通过建立重投影误差和约束区间的关系，自动调节约束区间，进而对位姿参数进行约束非线性优化；赵亚凤等[21]提出通过非线性优化确定两对正交消隐点的最优位置，进而求得双目相机的外参数。

针对相机位姿动态变化的自由双目立体视觉系统，本文提出了一种重投影优化的自由双目相机位姿估计算法。通过相机的位姿将空间三维点投影回图像坐标系，计算得到重投影位置坐标，重投影位置和该三维点在图像中实际成像位置间的距离，称为重投影误差。首先，利用平面标定靶立体标定初始位置双目相机的位姿；然后，在每次旋转后，根据上一个旋转位置的左右相机位姿，利用三角测量得到相邻两次测量间重叠区域内特征点的三维点云坐标；针对每个相机，利用旋转前后拍摄的两幅图像中的特征点匹配关系求解单应矩阵，将分解单应矩阵得到的相机运动参数作为初值，结合上一个旋转位置的相机位姿，将两幅图像重叠区域内的特征点点云重投影回图像坐标系，计算得到重投影误差之和，将其作为代价函数，利用列文伯格-马尔夸特(Levenberg-Marquardt, LM)算法优化代价函数，得到相机运动参数的最优解，进而获取相机旋转后的位姿。

2 自由双目相机位姿估计原理

自由双目立体视觉系统由两个可自由旋转的相机构成，它通过旋转扫描获取目标表面的分片点云，然后合成大场景的三维模型。自由双目立体视觉系统工作过程中，每个相机可自由旋转。如图1所示，第k次测量时，双目相机对Ωk区域成像，估计每个相机在世界坐标系的位姿信息并进行三维重建，得到Ωk区域的三维点云面片Ck。然后左右每个相机绕各自的旋转轴旋转，对Ωk+1区域成像，相邻两次测量之间有一定比例的重叠区域，利用重叠区域的特征点点云估计第k+1次测量时双目相机的位姿并进行三维重建，得到三维点云面片Ck+1。最后，将所有点云面片转换至世界坐标系中，实现点云拼接，得到完整场景的三维点云结构。左右相机位姿估计原理相同，以左相机为例，第k次测量时，左相机在世界坐标系下的位姿为 (Rlk,tlk)。相机绕旋转轴旋转一定角度到达第k+1次测量的位置，相机的旋转和平移运动用参数Rmotionl和Tmotionl表示，此时左相机的位姿定义为

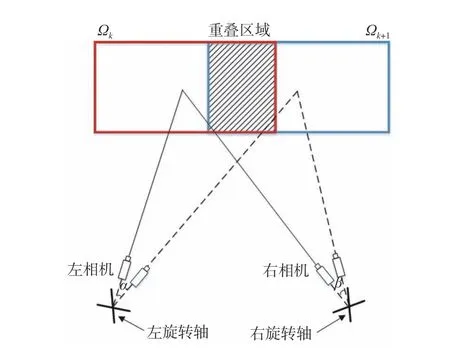
图1 自由双目立体视觉系统中相邻两次测量Fig.1 Two adjacent measurements of the free binocular vision system

在已知左相机运动参数 (Rmotionl,Tmotionl)和右相机运动参数 (Rmotionr,Tmotionr)的条件下，根据式(1)可以计算得到每次测量时左右相机的位姿。

3 基于重投影优化的自由双目相机位姿估计算法

3.1 旋转相机运动参数估计

由图1可以看出，相邻两次测量中单个相机主要做旋转运动，平移距离远小于成像距离，因此可以忽略相机平移带来的影响，将相机的运动近似为纯旋转模型，求解纯旋转相机的旋转矩阵，作为相机运动参数的初值，再利用非线性优化的方式得到运动参数的最优解。

假设P为空间中一个三维点，P投影到旋转前相机中的像点p1和 旋转后相机中的像点p2如式(2)所示，p1和p2均为齐次坐标，有

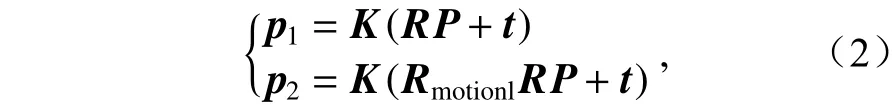
其中K表示相机内参数矩阵，(R,t)表示相机旋转前的位姿，由于相机做纯旋转运动，因此t在旋转后不发生变化，Rmotionl表示相机的旋转矩阵。

令相机旋转前的相机坐标系作为世界坐标系，则R为单位矩阵，t为零向量。将式(2)中的两式合并，可以得到p1和p2间的关系为

将KRmotionlK−1合并表示为矩阵H，即可得：

合并式(4)和式(3)可以得到两幅图像中匹配特征点间的对应关系为p2=Hp1。单应矩阵描述的是一组三维点在两幅图像间的变换关系，单应矩阵Hm和一对匹配特征点p1和p2的表达式为p2=Hmp1。 可以看出H和单应矩阵Hm的形式相同，因此可以通过求解单应矩阵的方式求解矩阵H。提取并匹配相机旋转前后拍摄的两幅图像中的特征点，根据匹配关系利用DLT算法求得单应矩阵H。在已知内参数矩阵的条件下，通过式(4)计算相机的旋转运动参数Rmotionl。

由于旋转矩阵是正交矩阵，而由式(4)得到的Rmotionl可能不满足该性质，因此可以利用SVD分解将Rmotionl转 化为正交矩阵的形式。对Rmotionl进行SVD分解，用单位矩阵代替Rmotionl的奇异值构成的对角矩阵，即可得到正交矩阵形式的Rmotionl。

3.2 重投影误差函数的构建

初始位置双目相机的相对外参数通过平面标定靶立体标定获得，将初始位置的左相机坐标系作为世界坐标系，得到左右相机在初始位置的位姿。双目相机第一次旋转后，根据相机的运动参数和在初始位置的位姿，利用重投影优化的位姿估计算法得到旋转后的相机位姿。之后每次旋转，都以上一个旋转位置的相机位姿为基础，计算当前位置的位姿。下面将介绍重投影误差函数的构建。

相邻两次拍摄间有一定的重叠区域，区域内的特征点点云坐标根据上一个旋转位置的双目相机位姿利用三角测量法[22]计算得到。Pi=为空间中位于相邻两次测量重叠区域的一点，根据相机在上个旋转位置的位姿和运动参数(Rmotionl,Tmotionl) ，点Pi重 投影回图像中的坐标为

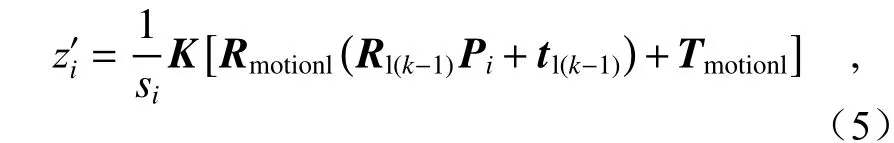
其中，K表示相机的内参数矩阵，si为将转化为齐次坐标的系数。

Pi在 相机旋转后采集图像中的实际成像位置为特征点zi，像素坐标为。点Pi的 重投影误差为实际成像坐标zi与 重投影位置坐标的差，即

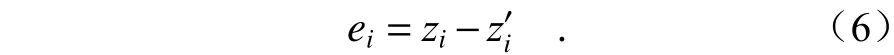
利用重叠区域内所有三维点的重投影误差距离平方之和构建目标函数，有

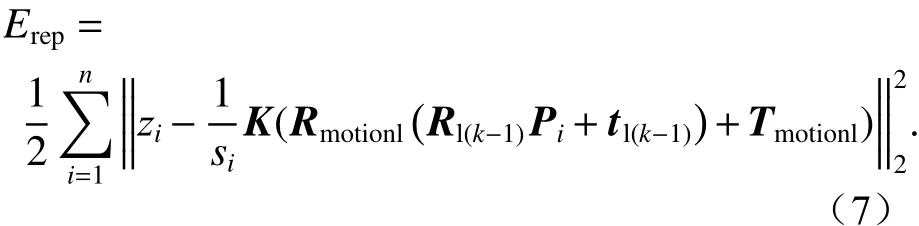
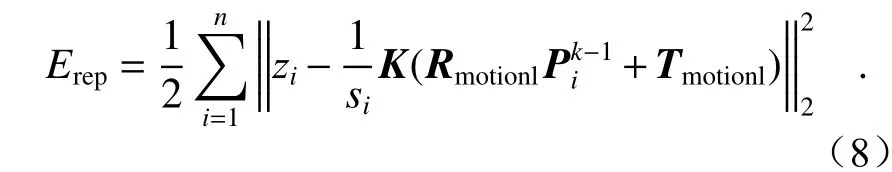
利用LM算法对目标函数进行优化，使重投影误差之和达到最小，即可得到左相机运动参数的最优解。同理可以得到右相机运动参数的最优解。

3.3 重投影优化的旋转相机位姿估计算法流程

将纯旋转运动下的相机运动参数作为初值，计算重叠区域内特征点云的重投影误差，以重投影误差距离之和构建待优化参数，作为相机运动参数的目标函数，利用LM算法优化目标函数至最小，即可得到相机运动参数的最优解，代入式(1)计算得到相机旋转后的位姿。基于重投影优化的自由双目相机位姿估计算法流程如下：

（1）标定初始位置双目相机的相对外参数，将左相机坐标系作为世界坐标系，确定双目相机的位姿(Rl0,tl0)和 (Rr0,tr0)，令k=1。

（2）由于左右相机位姿的估计方法相同，以左相机为例，根据相机第k次旋转前后拍摄的图像中特征点的匹配关系，利用直接线性变换法求解单应矩阵H。相机在纯旋转运动时，不发生平移，依据式(4)分解H得到相机旋转运动矩阵Rmotionl，作为相机运动参数的初值。

（3）依据上一个旋转位置的左右相机位姿，利用三角测量法重建两次拍摄间重叠区域内的特征点点云坐标，由式(5)计算特征点点云的重投影位置坐标，根据式(8)构建待优化参数为(Rmotionl,Tmotionl)的目标函数。利用LM方法对目标函数进行迭代优化，得到重投影误差最小时左相机运动参数的最优解。

（4）同理对右相机进行步骤（2）和步骤（3），得到右相机运动参数的最优解。将和分别代入式(1)，得到第k次旋转后的左右相机位姿 (Rlk,tlk)、(Rrk,trk) 。将(Rlk,tlk)和 (Rrk,trk)作为条件，令k=k+1，重复步骤（2）至步骤（4），即可得到每次旋转后左右相机的位姿。

4 实验结果及分析

4.1 位姿估计精度验证

利用opencv和ceres库进行仿真实验模拟。仿真实验中相机的等效焦距为96000 pixel，分辨率为5760 pixel×3840 pixel，参考点为在世界坐标系 区 域[−650, 650]×[−400, 400]×[24500, 25500]内随机分布的若干个点，单位为mm。仿真实验流程为：左相机光心位于世界坐标系原点，以朝向z轴正方向的位姿拍摄参考点图像，右相机光心位于(5000, 0, 0)位置，朝向(−1, 0, 5)方向拍摄参考点图像；模拟旋转轴偏离光心的情况，双目相机的旋转轴均位于沿着相机朝向的负方向偏离100 mm的位置，旋转轴方向与世界坐标系y轴平行；为保证1次旋转后双目相机的视场有50%的重叠比例，左相机绕旋转轴旋转2.1°，右相机绕旋转轴旋转1.7°，同时拍摄参考点图像。每种条件下重复运行50次仿真实验，消除参考点不同分布形式对位姿估计的影响，相机位姿的旋转和平移估计误差为[20]。

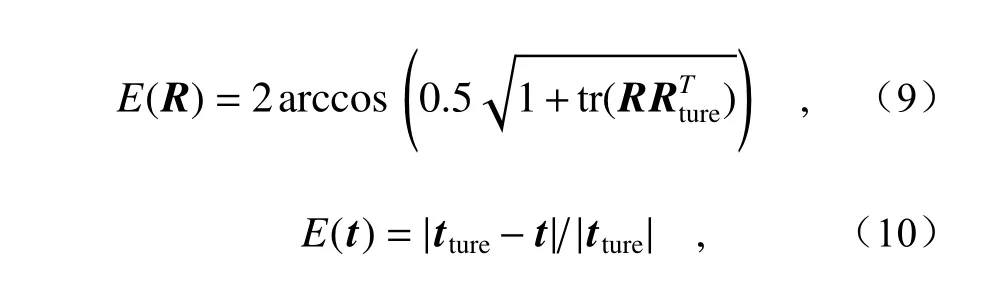
其中Rture和tture代表仿真实验中位姿的设定值，tr(·)代表矩阵的迹。

图2给出了旋转估计误差和平移估计误差随重投影误差的变化。为模拟实际拍摄中噪声的影响，在参考点成像时加入均值为0标准差为1的高斯噪声，实验中目标函数经过7次迭代达到最小。由图2可以看出，随着重投影误差的减小，旋转估计误差和平移估计误差逐渐减小，重投影误差最小达到69.87 pixel，此时旋转估计误差为0.03%，平移估计误差为0.07%。

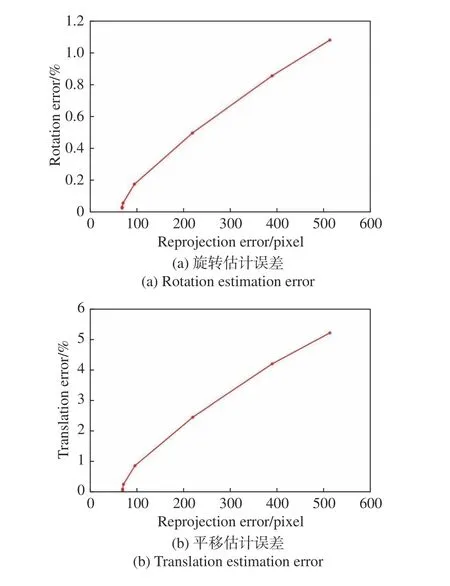
图2 位姿估计误差随重投影误差的变化Fig.2 Changes in pose estimation error with reprojection error

研究不同参考点个数和不同噪声条件下，利用所提算法和P3P+LM[19]方法估计相机位姿时，重投影误差代价的变化过程。实验中参考点个数分别为15、45、75，高斯噪声标准差σ分别为1、2、3，LM算法的迭代次数设置为50，得到结果如图3（彩图见期刊电子版）所示。结果表明，针对自由双目立体视觉中的相机位姿估计问题，所提算法相比P3P+LM能更快速、更稳定收敛于全局最优解。在实验条件下，所提算法收敛至全局最优解所需的迭代步数相比P3P+LM算法更少。原因是所提算法中传递给重投影优化的运动参数初值和全局最优值相近，更容易收敛；而P3P得到的位姿初始值相比真值误差较大，导致优化算法难以收敛。

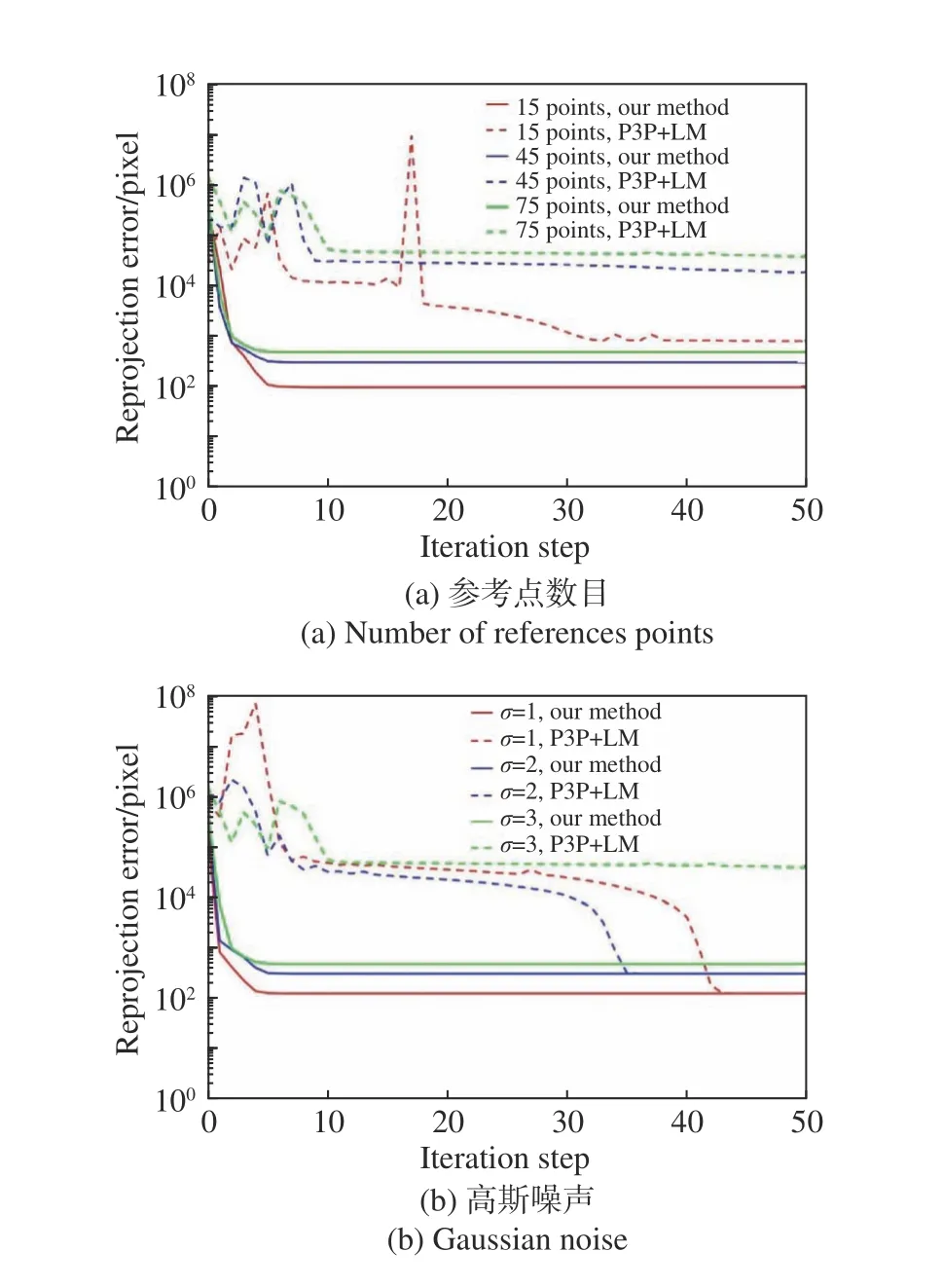
图3 不同条件下算法的收敛情况Fig.3 Convergence of the algorithm under various conditions

图4给出在不同参考点数目条件下，位姿估计误差的变化曲线。设置参考点数目为5～100，高斯噪声的标准差为3，计算平均估计误差。结果表明，随着参考点数目的增加，所提算法的位姿估计误差减小，在参考点数目大于55时，位姿估计误差趋于平缓，旋转估计误差约为0.095%，平移估计误差约为0.5%。

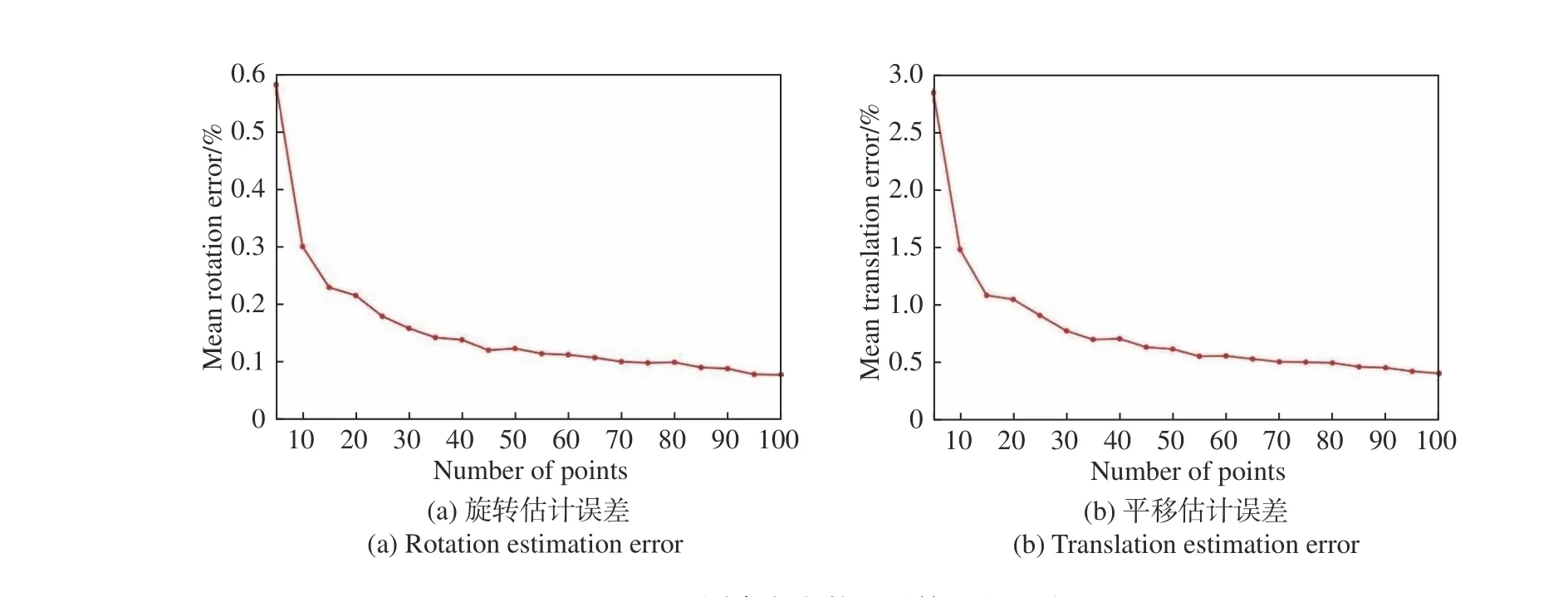
图4 不同参考点数目对算法的影响Fig.4 Changes in post estimation error to the algorithm with different numbers of reference points

图5给出在不同噪声条件下，位姿估计误差的变化曲线。设置参考点个数为100，高斯噪声标准差变化由0.5～5，计算平均误差。结果表明，随着噪声的增加，所提算法的位姿估计误差增大。在高斯噪声标准差不超过5时，旋转估计误差不超过0.14%，平移估计误差不超过0.8%。

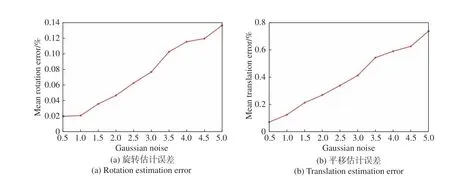
图5 不同噪声对算法的影响Fig.5 Changes in post estimation error to the algorithm under different noise

4.2 基于位姿估计的水泥模型重建实验

搭建自由双目立体视觉系统如图6所示，用两部5DMarkⅢ单反相机，分辨率为5760 pixel×3840 pixel，像元尺寸为0.00625 mm，镜头焦距为1200 mm（600 mm定焦镜头+2倍增倍镜）。综合考虑相机视场范围、系统的空间分辨率，系统基线设置为8.4 m，测量距离设置为48 m。分区域拍摄水泥模型的图像，估计每个位置的相机位姿，利用位姿进行三维重建并拼接点云模型，通过测量模型上特征点间距离，验证所提算法估计相机位姿的有效性。

图6 自由双目立体视觉装置图Fig.6 Diagram of free binocular stereo vision device

实验中计算机CPU为Intel Core i7-8700处理器，操作系统为Windows 10家庭版，采用Opencv实现图像处理相关功能，采用ceres库实现重投影优化功能。考虑到计算机的处理能力，实验中对拍摄的图像进行降4倍采样处理，图像分辨率变为1440 pixel×960 pixel。

实验过程为：首先，确定相机的内参数。根据镜头的物理焦距和像元尺寸计算得到等效焦距为48000 pixel，光心位于像面中心，由于长焦镜头的畸变较小，且成像距离较远，忽略畸变对成像的影响。利用每格宽度为60 mm的棋盘格平面标定靶对初始位置双目相机的相对外参数进行立体标定，棋盘格上有角点10行7列共70个，通过棋盘格标定确定平移向量的单位为mm，标定得到结果为(R0,T0)：

将初始位置的左相机坐标系作为世界坐标系，得到左相机位姿(Rl0,tl0)和 右相机位姿(Rr0,tr0)：

保持相机不动，采集水泥模型左半区域的图像。左右相机分别旋转一定角度对水泥模型中间区域进行拍摄，最后再旋转一定角度对水泥模型右半区域进行拍摄，3次拍摄得到图像如图7所示，其中第一行均为左图，第二行均为右图。

以左相机为例，针对第一次旋转，提取图7(a)和7(b)中的SIFT特征点，利用FLANN实现特征匹配，根据特征点匹配关系通过DLT方法求解单应矩阵Hl：

图7 双目相机采集图像Fig.7 Images obtained by binocular cameras

根据式(4)分解Hl，并将结果转化为正交矩阵形式，可以得到左相机旋转运动矩阵Rmotionl。

根据旋转前相机位姿 (Rl0,tl0)和 (Rr0,tr0)利用Opencv中triangulation函数重建图7(a)和7(b)重叠区域的特征点点云。相机在纯旋转运动时，不发生平移。将 (Rl0,tl0)和Rmotionl代入式(5)计算每个点云的重投影坐标，根据式(8)构建重投影误差目标函数。图7(c)和图7(e)分别为2次旋转后的左图和右图，利用LM算法优化目标函数至最小，得到左相机运动参数的最优解。同理，利用图7(d)和7(e)中的特征点匹配关系求解单应矩阵，分解单应矩阵得到右相机旋转运动参数Rmotionr，作为初值构建重投影误差目标函数，利用LM算法优化目标函数至最小，得到右相机运动参数的最优解

将 (Rl0,tl0)和代入式(1)，得到第1次旋转后的左相机位姿 (Rl1,tl1)。同理可得第1次旋转后的右相机位姿(Rr1,tr1)：

以第1次旋转后的相机位姿(Rl1,tl1)，(Rr1,tr1)作为已知，重复上述过程，同理得到第2次旋转后左相机位姿(Rl2,tl2)和 右相机位姿(Rr2,tr2)：

利用每次拍摄时左右相机位姿对模型每个区域进行三维重建，三维重建采用Opencv中的SGBM算法实现，得到结果如图8(a)～8(c)(彩图见期刊电子版)所示。根据每个拍摄位置的左相机位姿，将点云转换至世界坐标系下，实现三维点云的拼接，得到结果如图8(d)(彩图见期刊电子版)所示。利用Geomagic Studio 12在三维点云上对6个蓝色标志点的圆心进行提取，计算AB、CD和EF间距离。重复进行位姿估计和三维重建实验4次，得到结果如表1所示。

图8 三维重建结果Fig.8 3D reconstruction results

在实际模型上，用钢尺测量AB、CD和EF间的距离3次，得到实际测量距离的平均值分别为506.3 mm、204.5 mm和507.8 mm。由 表1知，计算得到AB、CD和EF相比实际测量距离的平均误差分别为1.12%、2.77%和1.14%，对3个误差取平均值，得到模型表面两点间的平均测量误差为1.68%。

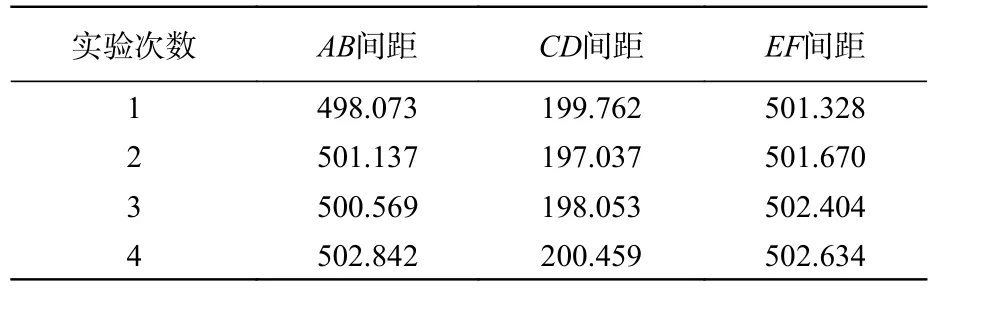
表1 标志点间距Tab.1 Distance between mark points （mm）

5 结论

本文针对自由双目立体视觉中遇到的相机自由旋转，导致位姿动态变化的问题，提出一种重投影优化的自由双目相机位姿估计算法。将相机运动近似为纯旋转模型，通过分解单应矩阵求解相机运动参数，将其作为初值构建重投影误差目标函数并进行优化，得到相机运动参数的最优解，结合相机旋转前的位姿，计算相机旋转后的位姿。该方法无需标定相机的旋转轴，不受限于对获取旋转台旋转角度的精度要求。通过仿真实验结果可知，利用所提算法得到相机位姿的估计误差随重投影误差减小而减小，所提算法相比P3P+LM算法能快速稳定收敛至全局最优；通过水泥模型的三维重建实验，拼接得到的三维模型上的两点距离平均测量误差为1.68%。本文所提算法可以用于解决自由双目立体视觉系统中的旋转相机位姿估计问题，进而实现大场景的三维重建。