受暂时性承压水作用的山前缓坡稳定计算公式推求*
章 校 阎长虹 郭书兰 谈金忠 徐成华 俞良晨 刘 羊
(①南京大学地球科学与工程学院, 南京 210023, 中国)
(②江苏省地质工程勘察院, 南京 210041, 中国)
0 引 言
宁镇地区新生代中晚期地壳运动以缓慢升降运动为主,山体长期接受风化剥蚀,形成诸多剥蚀残丘低山,山体周围多为相对平缓的缓坡,山前缓坡长期处于稳定状态,传统观念认为该缓坡是有利于山体稳定的“反压马道”。但2015年以来,由于受极端强降雨影响,山前缓坡地带发生了一系列滑坡地质灾害,如南京江宁方山、牛首山、游子山和镇江跑马山等缓坡滑坡(郜泽郑等, 2018; 刘羊, 2019; 阎长虹等, 2019; 俞良晨等, 2020)。
该类滑坡是一种山前松散堆积物土层中的滑坡,表现为缓慢滑动,阎长虹等(2019)对其形成机理进行研究,研究表明该类滑坡具有特殊地层结构,在极端强降雨影响下,坡体内会形成暂时性承压水,在承压水的浮托力作用下引发缓坡变形破坏,但如何推求和计算该类滑坡的稳定性系数尚未给出。这里尝试借鉴岩质平推式滑坡的计算方法作一探讨。张倬元等于1985年最早提出平推式滑坡的概念,并初步给出了平推式滑坡的启动判据(张倬元等, 2005); 李伟等(2017, 2018)提出敏感倾角的概念,并分析了不同透水层厚度、渗流量、渗透系数条件下岩层倾角的敏感性,指出边坡稳定性系数受滑面承压水渗流的影响很大; Matja et al. (2004)研究了斯洛文尼亚的两个平推式滑坡,发现此类滑坡主要是由长时间降雨形成的高水头承压水诱发的。Jiao et al. (2005)指出承压地下水对边坡稳定性影响很大,讨论了正确建立水文地质模型的重要性。一些学者研究了降雨对边坡岩土体性质的影响,Guo et al.(2020)指出强降雨条件下易溶岩地层内很有可能发育形成岩溶,孙萍等(2019)对黄土边坡开展了不同降雨条件下的现场试验研究,周家文等(2019)指出强降雨对滑坡发育及运动过程有深刻影响,这些研究表明强降雨是导致边坡岩土体力学性能降低的重要因素。还有一些学者采用了不同的极限平衡方法来分析边坡的稳定性,陈国华(2006)针对某滑坡使用Janbu法和传递系数法得出其稳定性系数,指出Janbu法考虑了条块受力全部平衡条件,其计算结果更为精确。杨志勇等(2019)探讨了极限平衡法在边坡稳定性评价中的适用性,指出不同形状的滑动面应选取不同的极限平衡方法计算。另外,针对平推式滑坡很多学者分析了地质结构、力学参数、几何尺寸、初始水力参数等在承压水模型中的影响(范宣梅等, 2008; 赵权利等, 2012; 涂园, 2018; 向云龙等, 2018)。以上研究主要是针对缓倾岩质边坡,而对缓倾土坡的讨论较少。为此,本文将以宁镇地区山前缓坡为基础,构建符合该地区水文地质条件的承压水模型,分析缓坡滑动机制,并基于Janbu条分法推导相应的缓坡稳定性系数公式。
1 山前缓坡特征
宁镇地区山体以剥蚀残丘为主,地貌形态以上陡下缓居多,如图1所示,上部主要为裸露基岩,受地壳构造运动作用岩体内裂隙十分发育,坡度较陡,多超过30°; 下部主要为残积土和松散堆积物构成缓坡,坡度多小于15°。2015年以来,受极端强降雨影响,在山前缓坡地带先后发生了多起滑坡。其山前缓坡滑坡基本特征如下:
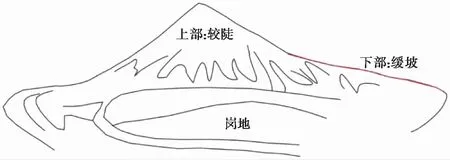
图1 宁镇地区山体地貌图
(1)在山前缓坡地带的滑坡规模达到中型-大型,滑坡体主要发生在山前松散堆积物中,滑坡后缘位于基岩和第四系松散层的交界处。
(2)山前缓坡地层结构特殊,颗粒成分下粗上细。坡体上部为厚度较大的粉质黏土层或含块石的黏土层; 黏土层以下为碎石土、砂砾石土、卵石土等粗颗粒土,透水性较好,易于赋存地下水; 粗颗粒土层以下为密实的黏土层或黏土岩以及全风化玄武岩。
(3)从各土层渗透性来看,上部填土、粉质黏土层和中部黏土层透水性较差,渗透系数在10-6cm·s-1左右; 粗粒土层及最底部的全风化玄武岩透水性较好,渗透系数在10-3cm·s-1左右,在极端强降雨条件下常形成暂时性承压水。
(4)从各土层强度参数来看,除浅表填土以外,其他土层的力学强度都比较高,其中碎石土层的内摩擦角在35°左右,远大于缓坡的坡度。
宁镇地区地属亚热带季风气候,温暖湿润,降雨集中在夏季,年平均降雨量1127mm(1996~2003年)。每年的6~7月份为梅雨季节,持续时间在20d左右,这段时间内降雨量较大,极端强降雨天气多发。2015~2016年宁镇地区经历了罕见暴雨天气,年降雨量达1960mm,远超往年平均降雨量。在此期间宁镇地区滑坡地质灾害显著增多,一些原本相对稳定的缓坡发生了滑动。显然,强降雨天气是诱发这些缓坡滑动的重要因素。
2 缓坡滑动机理分析
根据课题组对南京方山、猪头山、牛首山、金牛湖和镇江云台山、跑马山等山前缓坡的野外工程地质调查,发现这一地区的山前缓坡地层结构特殊,上部为不透水或弱透水黏性土,下部为透水性较强的碎石土或砾石土,后缘基岩裂隙发育。发生强降雨时,由于山体后缘坡度大而前缘坡度小,部分雨水形成坡面流流走,部分则进入山体后缘的基岩裂隙中形成基岩裂隙水,随着降雨持续,裂隙水会沿裂隙渗入至缓坡下部的粗颗粒土层中,构成山前缓坡内含地下水较丰富的含水层。而缓坡下部的黏土层较厚且不透水,使得地下水排泄受阻,此时缓坡内将形成暂时性承压含水层。暂时性承压水产生的浮托力将造成坡体顶托破裂或剪切破坏,从而出现随降雨而发生的间歇性蠕动滑坡。图2为缓坡地层结构示意图。

图2 缓坡地层结构
对宁镇地区山前缓坡进行稳定性分析,首先应确定其潜在滑面位置,由于缓坡表层黏土层为弱透水层,而下部砂砾土、碎石土中的承压水将对坡体浅表土层产生浮托力,因此坡体下部碎石土与浅表黏性土的交界面为潜在的滑面或软弱层,沿其面或层易发生滑动破坏,下面根据此潜在滑面基于Janbu条分法进行缓坡稳定性系数公式推导。
3 基于承压水模型的稳定性系数推导
3.1 水文地质模型分析
由上述分析可知,宁镇地区的山前土质缓坡具有类似“二元地层结构”的特征,下部为透水性较好的碎石土层,而上部为含块石或碎石的黏性土层,可按不透水层或弱透水层来考虑。在强降雨条件下,山体上部岩体裂隙水在重力作用下向周围粗颗粒土层渗透,由于黏土层渗透系数相比碎石土层小得多,可认为黏土层内的潜水由下部承压水垂直补给及坡面入渗补给。缓坡前缘大量堆积的黏性土透水性较差,遭遇极端天气时排泄通道很容易被堵塞,另外坡底处的房屋建筑也极大地减弱了地下水正常排泄。此时承压水将充满碎石土层,水头迅速升高,极端状态下可增至缓坡顶部土岩交界面处,暂时性承压水水头达到最大。这时山前缓坡的稳定性受暂时性承压水和潜水的共同影响,同时还应考虑后缘裂隙充水时产生的水平向推力,这是启动平推式滑坡的重要原因(张倬元等, 2005)。基于此,建立水文地质模型如图3。

图3 极端情况下承压水头与土条重量示意图
3.2 基于Janbu法的稳定性系数推导
由上述分析可知,山前缓坡的潜在滑面位于坡体浅表黏土层的底板或碎石土含水层的顶板,由于缓坡土层沉积分界面往往是高低起伏、不规则的向外倾斜面,故在缓坡稳定性二维分析中其滑面按折线考虑,此时使用圆弧条分法是不合适的(杨志勇等, 2019),这里选取Janbu法进行推导。首先将边坡体划分为若干条块,从中取任意土条i,如图4所示,土条的受力满足Janbu法基本假设。图中,Wi为土条重量,h1i、h2i分别为中心位置处潜水位上部和下部对应的土条高度;Ui为承压水浮托力,hi为中心位置处的暂时性承压水头高度;Ni、Ti分别为土条底面上的法向反力与切向反力;Xi、Ei分别为土条间的法向作用力与切向作用力;hti为法向条间力作用点的位置,位于土条底面以上1/3高度处,hti与hti+1的连线形成推力线;αti为推力线与水平线的夹角;αi为土条底面倾角;bi为土条宽度。

图4 条块受力示意图
考虑土条同时受到承压水及潜水的作用,这里先讨论承压水对缓坡稳定性系数的影响,暂时性承压水按浮托力垂直作用于土条底部来考虑。由于缓坡浅表土层透水性较差,在极端强降雨条件下缓坡内暂时性承压水头将高出坡面,即承压水不能在浅表黏土层中完全消散。其土条的受力情况如图4所示,其中土条重量Wi=γ土h土bi。承压水浮托力在条块底部呈梯形分布,如图5所示,当研究竖直或水平方向上力的平衡时,可用一个垂直作用于中点的集中力Ui等效替代,Ui=γwhili=γwhibi/cosαi,其中,li为土条底部滑面长度,γw为水的重度。

图5 土条底部浮托力示意图
3.2.1 缓坡中上部
由于缓坡地层界面随坡形向后缘逐渐抬高,故在缓坡中上部承压水头hi相对高度不高,有Wi>Ui,此时对土条i做以下分析。
取竖直方向上力的平衡,有:
(Ni+Ui)cosαi=Wi+ΔXi-Tisinαi
即
(1)
式中: ΔXi=Xi+1-Xi
取水平方向上力的平衡,有:
ΔEi=(Ni+Ui)sinαi-Ticosαi
将式(1)代入,有:
(2)
式中: ΔEi=Ei+1-Ei
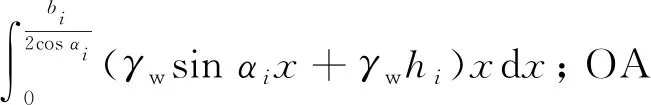
即
2Xi+ΔXi=-(2Ei+ΔEi)tanαti+
将高阶微量略去,得:
(3)
3.2.2 缓坡中下部
在缓坡中下部,承压水位相对高差较大,此时hi很高,有Wi 3.2.3 求解缓坡稳定性系数Fs 根据以上分析,在坡体中上部W1>U1i,坡体中下部W2 (4) 基于安全系数定义和Mohr-Coulomb屈服准则,有: (5) 联合式(1)和式(5)求解,得 (6) 式中: (7) 再将式(6)代入式(4),并将浮托力Ui=γwhibi/cosαi代入,可得其稳定性系数公式为: (8) 式中: 分子为临界点以上抗滑力的累加; 分母为缓坡整体下滑力的累加。与土力学中经典Janbu法稳定性系数计算公式相比(卢廷浩, 2011),浮托力Ui的存在,相当于在竖直方向上施加了向上的大小为γwhibi的压力,同时使得缓坡中下部区域内抗滑力消失,导致缓坡稳定性系数急剧减小。 此外,浅表黏土层由于受到承压水的垂直补给及坡面入渗补给,其内会产生潜水,此时缓坡还会受到潜水的作用。以上推导过程中,潜水仅对土条重量Wi一项产生影响,这里按水土合算法进行计算,即潜水位以上取天然重度γ,潜水位以下采用饱和重度γsat,亦即Wi=γh1ibi+γsath2ibi。将其代入式(8),可得到承压水和潜水联合作用条件下的稳定性系数公式: Fs= (9) 以镇江市跑马山山体西北侧某土质边坡滑坡为例(郜泽郑等, 2018; 刘羊, 2019),分析极端强降雨条件下承压水对缓坡稳定性系数的影响。该滑坡段坡体长约40m,宽约34m。根据工程地质测绘及钻孔资料,该缓坡地层由上到下大致可分为3层: ①粉质黏土,层厚0.6~16.9m,渗透系数在10-5cm·s-1左右; ②粉质黏土夹碎石,层厚2.2~5.3m,渗透系数在2.5×10-2cm·s-1左右; ③强风化石英闪长岩,层厚1.9~9m,渗透系数在10-6cm·s-1左右。缓坡某监测剖面如图6所示,根据前述分析,粉质黏土与粉质黏土夹碎石土层的交界面为潜在滑面,承压水沿此滑面对粉质黏土层产生浮托力。由三轴不固结不排水剪切试验给出,滑面以上粉质黏土层的黏聚力C为36.7kPa,内摩擦角φ为6.1°,天然重度为18kPa,饱和重度为19.7kPa。 图6 滑坡监测剖面图 表1 土条基本参数表 为得出跑马山边坡失稳临界状态水头,计算了不同承压水头下的边坡稳定性系数。其中:承压水头高程在19.831~24.9m变化,后缘裂隙水头对应为0~5.069m,计算时仍假定承压水头呈水平,这是偏于安全的。计算结果如图7所示,可以看出,缓坡的稳定性系数随着承压水头高程的增加而减小,曲线总体呈台阶状,台阶间较陡的原因是临界点以上提供抗滑力的土条数量发生改变,当土条划分更细时,曲线将变得平滑,跑马山边坡失稳临界状态承压水头高程在22m左右。当无承压水作用或承压水头较低时,该缓坡非常稳定,但若缓坡内形成高水头承压水,其稳定性将急剧降低,发生滑动破坏。 图7 不同承压水头下的稳定性系数 本文对宁镇地区山前缓坡滑坡机理进行了研究,分析了暂时性承压水诱发缓坡滑动的内在机理,讨论了极端强降雨条件下缓坡不同部位的受力差异,并根据Janbu法推导了缓坡在承压水和潜水联合作用下的稳定性系数公式,最后结合工程实例对比分析了承压水对缓坡稳定性的影响。得到主要结论如下: (1)宁镇地区山前缓坡具有类似河流相的“二元地层结构”,基于此可构建类似岩质边坡的承压水模型。但缓坡段黏土层和砂砾土、碎石土层渗透性差异很大,强降雨条件下承压水头可能高出坡面。 (2)受承压水浮托力的作用,缓倾土坡中下部区域抗剪力会减小甚至完全消失,与上部差异性很大,且其滑面位于不透水层底面或含水层顶面,呈非直线型不规则形状,故采用圆弧条分法进行计算显然是不合理的。因此,本文采用Janbu条分法进行稳定性计算更为合理。 (3)若坡体后缘存在大量裂隙水,或者渗流出口被堵塞,会导致承压水头迅速抬升,大幅降低边坡稳定性,造成坡体发生失稳甚至滑动破坏。因此,此类边坡工程的防治重点应为降低或消除承压水头,注意减少雨水大量入渗裂隙,同时及时疏通薄弱地层垮塌区,让地下水能够有效排泄。4 算例分析




5 结 论

