智慧公路设备横梁风振特性研究

成 晟

(泰州市公路事业发展中心，泰州 225300)

随着智慧公路发展，道路上的电子设备日益增多，设备横梁多为定型钢管，采用门架式或悬臂式，安装在路侧或道路上方。设备自重较轻，横梁承载能力一般都满足要求。但运营过程中发现，部分道路上空的设备横梁会发生上下振动的现象，影响设备使用，还可能带来安全隐患。

目前对振动问题的分析多采用有限元法，有限元法方便建模，随着计算机算力提高，近些年得到了广泛应用[1-2]，但有限元计算只能得到数值解，不能得到解析解，不便对结果进行数学解释和原因分析。

本文基于等截面直梁的横向振动模型，对门架式设备横梁和悬臂式设备横梁的振动进行了分析，得到的振动影响因子可以为结构设计提供参考。

1 振动特性分析

发生振动的门架式横梁为等截面八角钢管，跨径22.5 m，跨中处采用法兰对接，门架横梁结构如图1所示。安装设备后，测得振动周期大约为0.55 s，对应的角频率为11.42 rad/s。

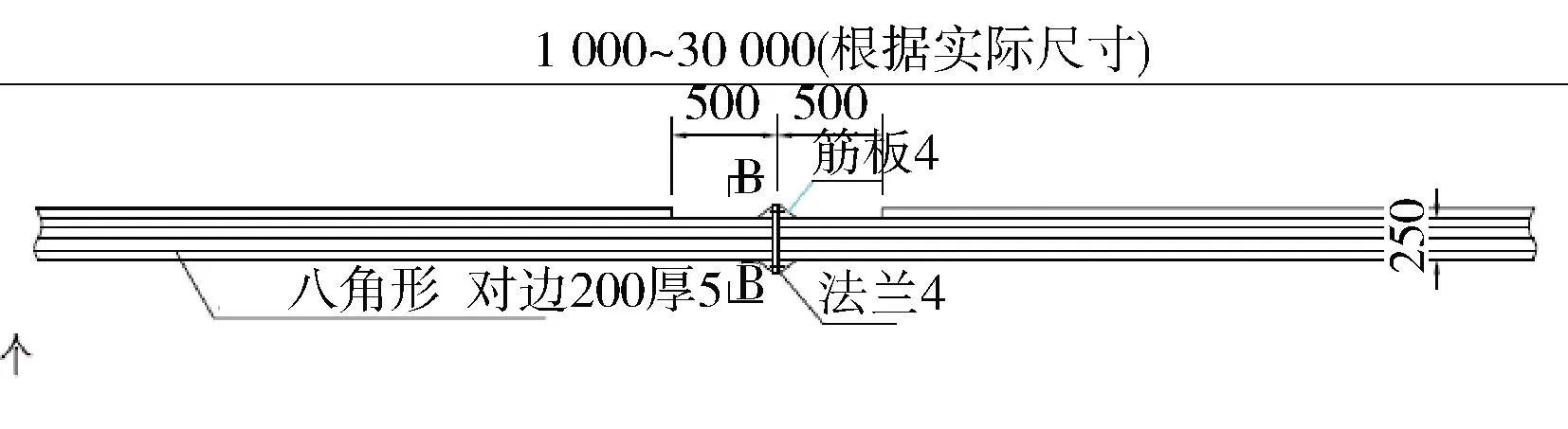
(a)立面结构(mm)

悬臂横梁结构实景如图2所示。悬臂式横梁为跨径7.25 m的圆管，外径15.9 cm，壁厚6 mm，尚未安装设备，测得振动周期大约为0.32 s，对应的角频率为19.63 rad/s。

图2 悬臂横梁结构实景

观测发现，横梁振动有如下特征：

(1)振动时风速不大。

(2)不同时段的振幅不同，但频率基本相同。

(3)横梁上各点虽振幅不同，但相位始终相同，沿纵向不发生能量传播，具备典型的驻波特征。

2 两端固结等截面直梁的横向振动

2.1 无阻尼自由振动

直梁横向自由振动作为振动力学的经典问题，已有较多研究成果[3]。假设横梁为欧拉-伯努利梁，不考虑截面的剪切变形和截面绕中心轴转动的惯性效应。微元体受力如图3所示。

图3 微元体受力

弯矩和剪力的计算公式分别见式(1)和式(2)。

(1)

(2)

式中，M为弯矩，N·m；Q为剪力，N；w为横向位移，m；E为杨氏模量，N/m2；I为截面惯性矩，m4；x为纵向距离，m。根据式(1)和式(2)可推导出等截面直梁的横向自由振动方程，见式(3)。

(3)

式中，ρ为材料密度，kg/m3；S为截面积，m2；t为时间，s。

采用分离变量法，令横向位移为

w(x,t)=φ(x)q(t)

(4)

代入式(3)，得到

等式两边同时除以ρSφ(x)q(t)，并令

得到

(5)

EIφ(4)(x)-ρSω2φ(x)=0

(6)

式中，wi为固有频率，rad/s。

式(5)为单自由度线性振动方程，其通解为

q(t)=αsin(ωt+θ)

(7)

φ(4)(x)-β4φ(x)=0

(8)

利用指数形式特解φ(x)=eλx，代入式(8)可导出特征方程λ4-β4=0，继而求得式(8)的通解为

φ(x)=C1cosβx+C2sinβx+C3chβx+C4shβx

(9)

式(7)和式(9)中的C和ω由梁的边界条件确定，理论上存在无穷多个固有频率ωi和对应的振型函数φi(x)。

一维简谐波的驻波方程为

y=2Acoskxcosωt

(10)

式(10)中时间变量和位置变量相互独立，表明各点的振动状态不发生纵向传播。对照式(4)和式(10)可知，分离变量解和驻波方程在形式上基本相同，因此振动横梁上的驻波可看作式(3)的一个特解或几个特解的叠加。当外部激励力频率ω0和系统的第k阶固有频率ωk接近时，第k阶主坐标振动幅度急剧增大，产生第k阶频率的共振，并可近似忽略其他非共振的主坐标[3]。

边界条件：固定端的位移和转角都为0，即

φ(x)|x=0=0，φ(x)|x=L=0

φ′(x)|x=0=0

φ′(x)|x=L=0

(11)

式中，L为杆长，m。

代入式(9)，得到两端固结等截面直梁横向振动的控制方程为

cosβLcoshβL-1=0

(12)

将横梁参数代入控制方程，通过数值求解，得到i为1、2、3时的角频率ω分别为16.05 rad/s、44.25 rad/s、86.75 rad/s，以纵向位置x为横坐标、相对振幅为纵坐标，可求得对应的振型，横梁振型如图4所示。实际横梁的固有频率受材料、结构、设备质量和施工误差影响，和理论值存在偏差。

(a)i=1

因实际振动的横梁上各点相位始终相同，故横梁驻波主要对应于i=1时第一振型的共振。

2.2 阻尼自由振动

无阻尼自由振动是一种理想情况，实际系统不可避免存在阻尼因素。等截面直梁的横向阻尼振动方程为

(13)

式中，c为黏性阻尼系数，N·s/m。

采用分离变量法，将式(4)代入式(13)，得到

(14)

等式两边同时除以ρSφ(x)q(t)，并令

得到

(15)

(16)

将特解q(t)=eλt代入式(16)，求得当ζ<1，系统处于欠阻尼状态时的通解

q(t)=Ae-ζωtsin(ωdt+θ)

(17)

式中，A为初始幅值，m；θ为初相角，rad；ωd为阻尼自由振动的固有角频率，rad/s。

(1)阻尼自由振动的振型函数φi(x)与无阻尼自由振动相同。

(2)因ωd<ω，故阻尼自由振动频率小于无阻尼自由振动频率。

(3)振幅与-ζωt呈指数关系，阻尼和固有频率增大，都将导致阻尼自由振动的振幅迅速衰减。

2.3 受迫振动

实际横梁振动是在外部荷载的持续激励下产生的，因此需要对横梁的受迫振动进行计算。因系统固有振型与阻尼、外部激励无关，故可假设外荷载的空间分布与振型函数相同，以方便计算。

令外部激励力为

F(t)=F0φ(x)eiω0t

(18)

F和F0单位为N，则受迫振动方程为

=F0φ(x)eiω0t

(19)

采用分离变量法，将式(4)代入式(18)，得到

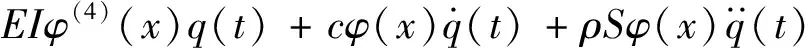
=F0φ(x)eiω0t

(20)

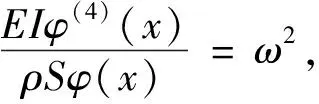
(21)

根据常微分方程理论，非齐次线性常微分方程式(21)的全解由齐次线性方程(15)的通解和非齐次线性方程(21)的特解两部分组成。通解为阻尼自由振动，由于自由振动只在扰动初期短暂存在，随即趋于衰减，故只需讨论非齐次线性方程(21)的特解。简谐激励引起的稳态响应也是简谐运动，故可令解的形式为q(t)=Qeiω0t，代入式(21)求得特解为

(22)

式中，f=ω0/ω为激励频率与固有频率之比(无量纲)。

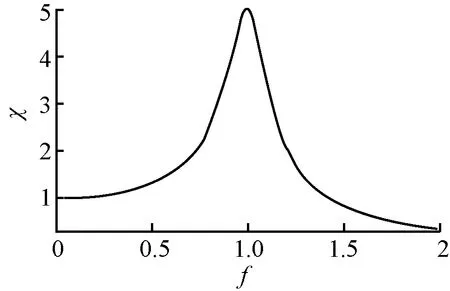
(a)ζ=0.1

由式(22)可知：

(1)受迫振动频率和外部激励频率相同。

(2)受迫振动振幅受固有频率、激励频率和阻尼影响，与固有频率平方呈反比关系。当激励频率与固有频率比值接近1时，振幅急剧增大；阻尼增大时，振幅放大因子减小。

2.4 计算分析

悬臂梁的边界条件为：固定端的位移和转角为0，自由端的弯矩和剪力为0。除边界条件外，悬臂梁的振动方程和解析步骤与两端固结等截面横梁完全相同，故不再赘述。

代入横梁实际尺寸，可求得自由振动情况下，门架式横梁的固有振动周期为0.39 s，悬臂式横梁的固有振动周期为0.34 s。

悬臂式横梁的计算周期与实测周期接近，而门架式横梁的计算周期与实测周期偏差较大，分析可能是因为悬臂式横梁尚未安装设备，而门架式横梁上已安装设备，设备会影响横梁的固有振动频率。

3 风荷载分析

在一定条件下的定常来流绕过钝体时，物体两侧会周期性地交替脱落旋转方向相反、排列规则的双列线涡，称为卡门涡街。由于旋涡交替脱落，产生的脉动荷载会使结构发生受迫振动[2, 4]。

空气的雷诺数Re(无量纲)[5]计算公式为

Re=69 000vd

(23)

式中，v为计算流速，m/s；d为截面直径，m。若圆柱体直径取0.2 m，当风速为0.02～21.7 m/s时，代入式(23)可求得对应的雷诺数为300～300 000。

圆柱体的旋涡脱落频率[6-7]为

(24)

式中，T为脱落周期，s；D为圆柱外径，m；St为斯特劳哈尔数(无量纲)，主要与流体的雷诺数有关，当雷诺数为300～300 000时，St近似于常数值0.2[4]。

将外径0.2 m、脱落周期0.55 s代入式(24)，不考虑横梁上设备影响，求得门架式横梁振动时对应的风速为1.82 m/s。将外径0.159 m、脱落周期0.32 s代入式(24)，求得悬臂式横梁振动对应的风速为2.48 m/s。江苏泰州地区重现期10年的风速为24.5 m/s[5]。因此，设备横梁会在风速较小时振动，与实际观测一致。

4 固有频率影响因子分析

4.1 尺寸影响分析

因八角钢管与圆管外形相似，故本节用圆管代替八角钢管进行模拟计算，取不同外径、壁厚和跨径组合，分别计算门架式横梁无阻尼自由振动的固有频率。固有频率ω与外径D呈正比关系，与跨径L的平方呈反比关系，与壁厚无关，门架式横梁固有角频率影响因子如图6所示。

图6 门架式横梁固有角频率影响因子

固有频率ω与外径D和跨径L的关系为

(25)

式中，ω为固有频率，rad/s；D为外径，m；L为跨径，m。

同样可求得悬臂式横梁固有频率与外径、跨径的关系。悬臂式横梁固有角频率影响因子如图7所示，计算公式见式(26)。

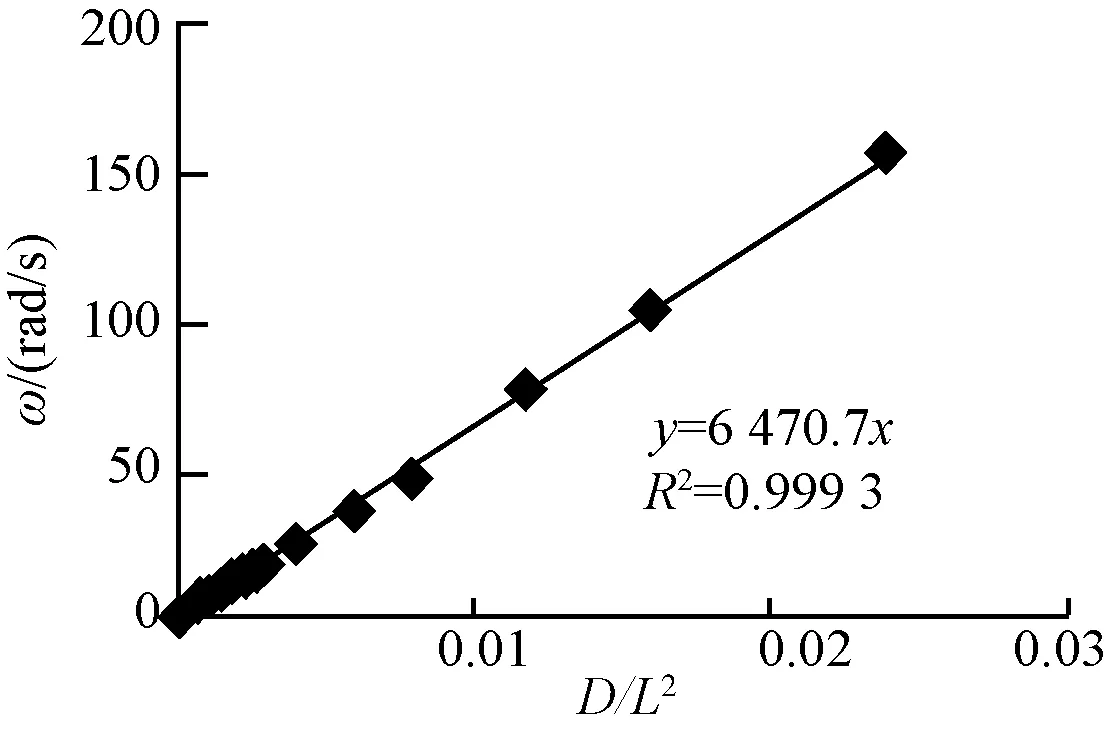
图7 悬臂式横梁固有角频率影响因子

(26)

由式(25)和式(26)可知，加粗钢管或减小跨径都能提高固有频率。

风速增大时，旋涡脱落频率随之增大，并接近部分小跨径横梁的固有频率，但实际并未发现这类横梁有明显振动，这是因为式(22)中振幅与ω2呈反比关系，跨径减小后固有频率增大，抑制了受迫振动的振幅。

4.2 质量影响分析

为模拟设备质量对横梁振动的影响，保持横梁尺寸不变，改变横梁密度，考察自由振动的固有频率变化，质量对门架式横梁固有角频率的影响如图8 所示。

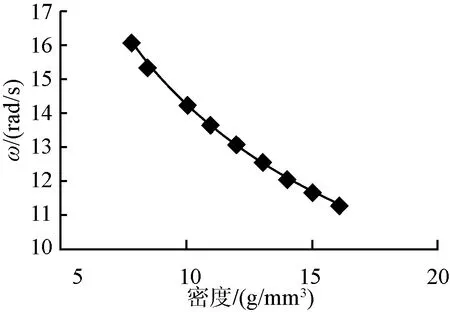
图8 质量对门架式横梁固有角频率的影响

由图8可知，固有频率随密度增加而减小。因此，设备安装后，横梁的固有振动周期增大，对应的共振风速减小。

5 防治措施

通过以上分析可知，受迫振动的振幅主要受固有频率、激励频率和阻尼3个因素影响，为减少横梁振动可考虑下列3种措施。

5.1 提高固有频率

固有频率与钢管外径成正比，与跨径平方成反比。通常跨径无法减小，增加钢管外径不经济。因此，可将单钢管横梁结构改为双钢管桁架结构来增加结构刚度。

5.2 增加阻尼

参考桥梁设计方法，增设横向拉索或阻尼设置[6]；参考汽车行业，在梁上敷设约束阻尼层，通过振动时两个表面层的相对位移增加阻尼[8]。

5.3 改善气动外形

通过优化截面形状、改变表面粗糙度，或在表面设置螺旋线，达到抑制涡振的目的[2, 6, 9]。

6 结论

本文通过分析等截面直梁横向振动，证明了智慧公路设备横梁振动为风荷载下的驻波，进而建立了横梁受迫振动振幅与固有频率、外部激励频率和阻尼的数学关系。经计算发现横梁固有频率与钢管外径成正比，与跨径的平方成反比，随设备质量增加而减小。通过风荷载分析证实设备横梁的振动频率与风在横梁处绕流时的旋涡脱落频率一致，当脱落频率与横梁固有频率接近时，横梁将发生大幅振动。增大结构刚度、增加阻尼或改善结构气动外形能抑制横梁振动。