基于超弹性本构参数识别的橡胶衬套耐久性仿真研究

程稳正 张志远 徐京涛 楼位鹏 刘海峰

（吉利汽车研究院（宁波）有限公司，宁波 315000）

主题词：橡胶衬套 块谱 静刚度 超弹性本构 参数优化 疲劳寿命

1 前言

橡胶衬套的耐久性开发一直是整车耐久性开发的难点问题之一。橡胶衬套耐久性仿真预测与道路试验的关联性较差，原因主要体现在2个方面。一是载荷条件。由于衬套变形的非线性，直接施加路谱载荷时域信号求解应变历程，计算资源消耗巨大，难以实施，需要将载荷时域历程信号通过损伤等效的方式转换成块谱信号，在此基础上进行疲劳寿命预测，因此，块谱转换结果与路谱的关联性直接决定了仿真、块谱台架试验结果与路谱的关联性。二是本构参数。对于橡胶衬套寿命预测，目前有多种疲劳分析理论，如裂纹扩展法、裂纹萌生法等[1]，但其关键在于用于计算损伤参量的应变的计算，而这需要橡胶材料的超弹性本构参数作为基础。描述橡胶材料的超弹性方程类型众多，如Mooney-Rivlin、Ogden、Yeoh 等[2]，各本构模型基于一些参数进行描述，获取这些参数值，需要进行一系列试验[3]。在项目开发前期，往往只有某种胶料的测试数据，或者只有部分试验数据，无法准确获取能描述衬套力学行为的本构参数。

本文为解决某车型道路试验中扭力梁衬套开裂的问题，基于虚拟试车场仿真道路载荷谱编制扭力梁衬套的三轴块谱，作为衬套疲劳仿真和台架试验的载荷输入，按Mooney-Rivlin 模型和Yeoh 模型计算衬套的2 个径向（空心、实心）、轴向刚度，以初始本构参数为输入，以衬套静刚度特性曲线为目标，通过多目标优化得到能准确体现衬套宏观刚度特性的超弹性本构参数，以Yeoh 本构模型仿真得到衬套在块谱载荷下的应变，通过裂纹扩展法预测其寿命。

2 扭力梁衬套块谱转换

对于橡胶衬套块谱转换，陈芦等研究了橡胶悬置单轴荷谱编制方法[4]，芦勇等研究了副车架衬套多轴道路载荷谱缩减方法[5]。这些方法的主要转换过程为：

a.利用有限元分析或者基于衬套刚度特性曲线将路谱载荷信号转换为位移信号；

b.选取关键通道分别进行有限元分析，通过多项式拟合得到关键通道各自的应变与位移关系表达式，并将位移信号历程转换为应变信号历程；

c.对应变信号历程进行雨流计数得到损伤矩阵，在此基础上进行应变块谱转换；

d.将应变块谱转换结果反推至力载荷，形成力载荷块谱。

本文在该方法的基础上，提出采用工程等效应变代替步骤b 中的应变-位移关系拟合，可以更好地考虑各通道载荷之间的耦合效应。本文采用的虚拟试车场（Virtual Proving Ground，VPG）仿真路谱，包含了各通道的力和位移信号，省去步骤a，提出基于工程等效应变进行雨流计数得到损伤矩阵的方法代替步骤b、c 中的方法，可以综合考虑各通道的耦合作用。

2.1 路谱载荷

扭力梁橡胶衬套VPG道路载荷通道包括力-力矩、位移-角度总计12 个通道，共计35 条路面载荷数据。每条路面数据去除连接路面，考虑载荷循环后，整个载荷历程总时长约为140 h，各路面单个循环串联后的载荷谱如图1所示。台架验证如以路谱形式复现，在夹具设计、加载方法上均难以实现，且试验周期长。工程实践中运用块谱转换技术，如图2 所示，将该试验过程尽可能减化、压缩，同时需保证相位、频率与路谱载荷保持一致。

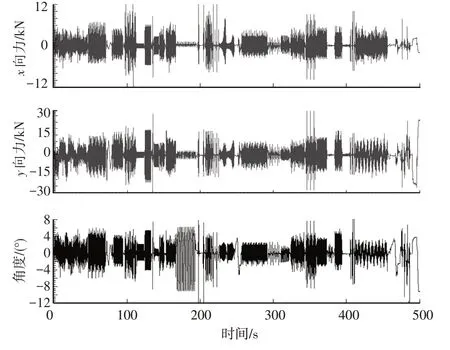
图1 通道载荷历程

图2 衬套块谱转换过程

2.2 通道筛选

扭力梁衬套路谱载荷包含12 个通道，载荷转换方法的选取需要考虑衬套实际受力情况：扭力梁衬套运动过程中衬套扭转角度由悬架系统运动决定，因此衬套扭转角度与衬套自身扭转刚度基本无关，扭转情况宜选用角度而非力矩；同样的情况下，对于力-位移这一对载荷，衬套刚度不同，应对外部冲击反映出的位移变化差异显著，应该使用力而非位移。

载荷转换类型选定力-角度，总计6向载荷，而试验设备最多能够实现3向载荷同时加载。因此，需进一步从6 向通道中选取损伤最大的通道转换块谱。常规做法是通过计算伪损伤或根据经验判断，该方法存在以下缺陷：不同类型载荷不能直接进行对比；实际损伤与伪损伤之间存在不确定性，应力/应变在各向载荷同量、同性时，才具备可比性；丢弃的通道的影响无法量化，更不能进行量化修正。

因此本文提出工程等效应变来解决此类问题，工程等效应变即衬套的名义应变E，结合衬套的实际结构、危险点、位移等计算，用以衡量各通道载荷的影响，其表达式为：

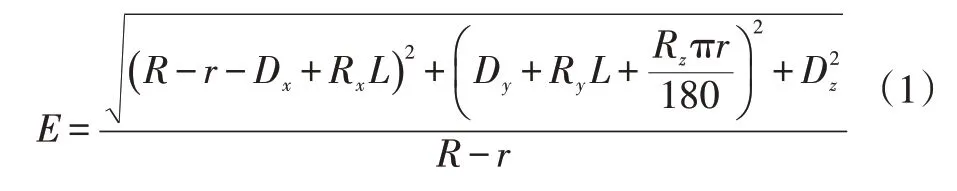
式中，R、r分别为橡胶层的外径和内径；Dx、Dy、Dz分别为衬套在x、y、z方向的平动位移；Rx、Ry、Rz分别为衬套绕x、y、z轴的旋转角度；L为衬套的轴向长度。

对于衬套危险点，通过空间位置、几何位置关系计算其等效总应变，同时使用该方法计算得到任一通道等效应变。以此为基础，可量化不同载荷的具体影响，筛选试验加载通道，量化去除通道载荷对橡胶衬套的影响，块谱载荷可根据该量化值适当缩放选取的通道载荷以补偿该影响。

根据工程等效应变的计算结果，选择用于块谱转换的通道为整车x向、y向载荷和扭转载荷。

2.3 通道解耦

根据工程等效应变，求解各试验路面、各硬点对应通道载荷的伪损伤、载荷范围，根据各路面各载荷通道的损伤占比（路面损伤与所有路面损伤和的比值）、载荷范围比（路面载荷范围与所有路面最大载荷范围的比值），去除个别通道路面损伤占比较小、载荷范围比也小的7条路面数据。对于保留的28条路面数据，按纵向力Fx、侧向力Fy和扭转角度Ry的损伤分布、载荷范围情况进行统计，通过排列组合，得到单轴（1个载荷通道）、双轴（2 个载荷通道同时输入）和三轴（3 个载荷通道同时输入）工况，各工况路面数量如表1所示，同一种工况的路面，只需对关注的通道进行转换。

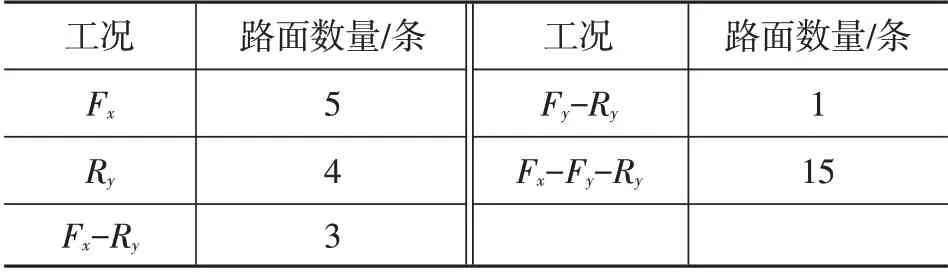
表1 工况组合

2.4 块谱转换

基于转换通道、等效总应变结果，对相应通道载荷进行块谱转换，目标为等效总应变雨流特征（程对（Range Pair）计数、穿级（Level Crossing）计数等），提取对应转换通道载荷并在此基础上补偿去除通道的影响，根据载荷特征整理形成衬套台架试验载荷块谱。图3所示为转换完成的块谱等效总应变与路谱的穿级计数比较，可以看出，块谱与路谱基本等效，认为该块谱转换结果与路谱载荷接近，可用于衬套的台架试验及仿真计算。

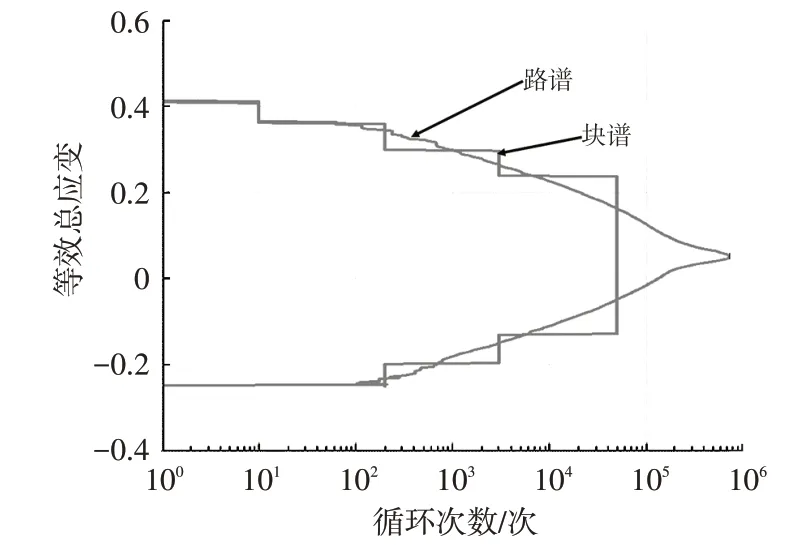
图3 等效总应变对比

橡胶衬套对载荷频率比较敏感，采用不同的加载频率会得到不一样的试验结果，为了保证台架试验与VPG仿真结果尽可能一致，需要计算块谱加载频率。试验加载频率相对固定，可以通过计算载荷-频率分布区间来确定块谱载荷加载频率，台架试验可以分别按2 Hz、4 Hz、5 Hz进行加载。

3 橡胶超弹性本构参数识别与优化

针对基于试验数据的橡胶超弹性本构类型选择和参数识别，众多学者进行了研究，并指出了各种模型的适用范围[6-7]。当没有测试数据或者数据不全时：文献[8]通过以主受力方向线性刚度为基准对第三方向刚度进行检验，并不断迭代的方式优化本构参数；文献[9]、文献[10]利用衬套刚度曲线，设定力-位移曲线面积、固定点取值为优化目标，结合有限元方法获取较优本构参数。本文采取刚度曲线逼近的方式优化本构参数，即在2 个径向和轴向共3 个刚度曲线上分别取6 个逼近点，以目标曲线与仿真曲线差值最小为目标，通过试验设计（Design of Experiment，DOE）识别能描述衬套宏观刚度特性的本构参数，为后续寿命预测提供基础，流程如图4所示。

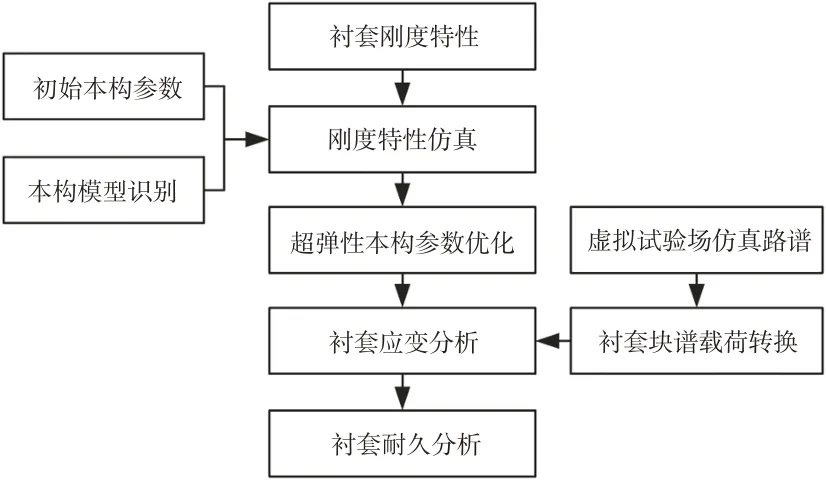
图4 衬套寿命预测流程

3.1 超弹性本构方程

对于密实橡胶材料，基于唯现象论的模型，不考虑微观结构，建立数学框架来表征其宏观上观察到的应力-应变关系，主要模型有Reduced Polynomia、Neo-Hookean、Mooney-Rivlin、Ogden、Yeoh 等。文献[6]、文献[7]中提到采用Mooney-Rivlin、Yeoh 模型，在宏观上能较为精确地表征橡胶衬套刚度，本文以这2种模型为基础，进行参数识别与优化。

Mooney-Rivlin模型为[7]：

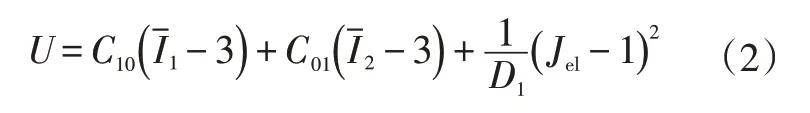
式中，U为应变势能；C10、C01、D1为材料常数；、分别为第1、第2阶应变不变量；Jel为弹性体积比。

Yeoh模型为3阶多项式缩减模型[7]：

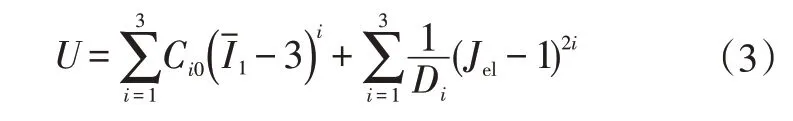
式中，Ci0、Di为材料常数。

文献[11]中提到，C10代表小应变下的初始剪切模量，负值的C20体现中应变下的软化过程，C30控制大应变下的曲线上扬，可以较好地捕捉橡胶材料的刚化效应，当Di=0，且Jel=1时，实现材料完全不可压缩。

基于以往材料测试数据，定义2个模型的初始参数分别如表2、表3所示。

表2 Mooney-Rivlin模型初始参数

表3 Yeoh模型初始参数

3.2 初始静刚度分析

采用六面体实体单元建模，橡胶层与金属层的硫化粘结采用共节点或者定义绑定（Tie）接触的方式模拟，橡胶内部空隙建立自接触。根据橡胶衬套刚度测试方法建立边界条件，约束施加在衬套内套管，衬套外管建立刚性多点约束单元，载荷施加在刚性单元主点。扭力梁衬套的有限元模型如图5所示。

图5 静刚度分析有限元模型

应用表2、表3 中的初始本构参数对橡胶衬套进行静刚度分析，分别计算衬套的各向刚度，载荷位移曲线如图6 所示，可以看出，采用初始参数计算的衬套刚度较试验值低，初始本构参数不能描述衬套的刚度特性。

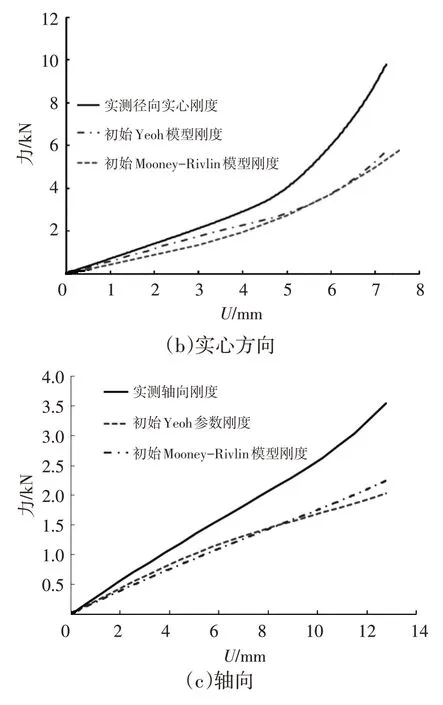
图6 初始参数仿真与试验对比

试验与仿真刚度结果存在差异的主要原因包括：材料模型不准确；工艺因素导致的几何差距；有限元简化造成的差异，如网格划分、边界条件简化等。显然，材料模型不准确是主要原因。

3.3 超弹性本构参数多目标优化

虽然基于初始本构参数的有限元仿真结果与实际结果存在偏差，但是可以利用计算得到的刚度特性与测试结果的差异，通过曲线对比，设定优化目标，并通过迭代求解对本构参数进行优化，优化过程如图7所示。

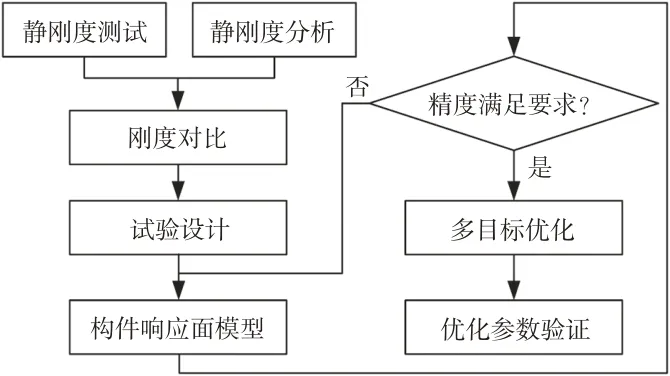
图7 超弹性本构参数优化流程

Mooney-Rivlin 模型具有双剪参数，对于中等程度的应变有较好的贴合效果，存在C10、C01、D13 个优化参数，对于橡胶材料，定义D1=0 表示不可压缩，因此优化变量为2个。Yeoh模型以C10、C20、C30为优化变量。

采用优化拉丁方进行试验设计，为提高计算效率，采用构造响应面近似模型的方法求解。响应面模型方差一般要求大于0.9，本文的响应面近似模型方差为0.995，满足误差要求，可在近似模型的基础上优化超弹性本构参数。

通过优化参数的全局效应图，观察优化参数对刚度的贡献程度，例如对刚度曲线线性段的贡献度大小依次为C10＞C20＞C30，结合仿真初始刚度与目标刚度的差距，确定优化变量取值范围如表4、表5所示。

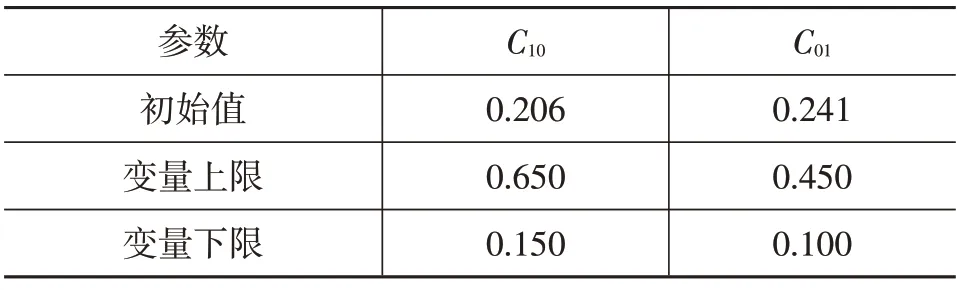
表4 Mooney-Rivlin模型变量取值范围

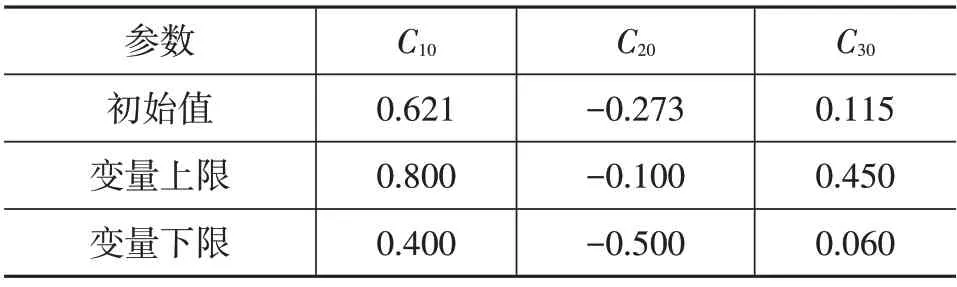
表5 Yeoh模型变量取值范围

在初始仿真参数计算得到的刚度曲线上取若干点来构造优化目标，如图8所示，其中一个方向刚度选取6个采样点逼近，其他2个方向刚度曲线采样点选取方法一致，进行多目标优化，以采样点仿真支反力与试验载荷差值之和最小为目标，根据变量范围进行迭代求解，收敛过程如图9所示。

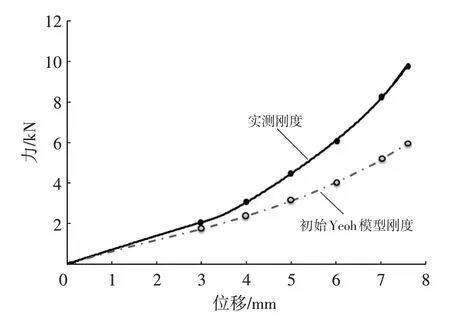
图8 刚度曲线逼近采样点

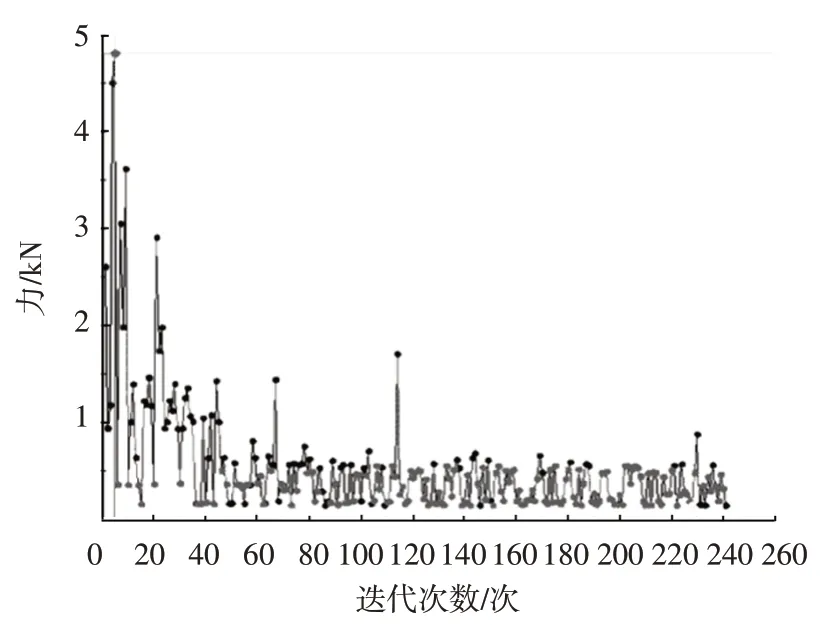
图9 优化迭代历程曲线

经过228 次迭代，求得最优的超弹性参数，结果如表6、表7所示。

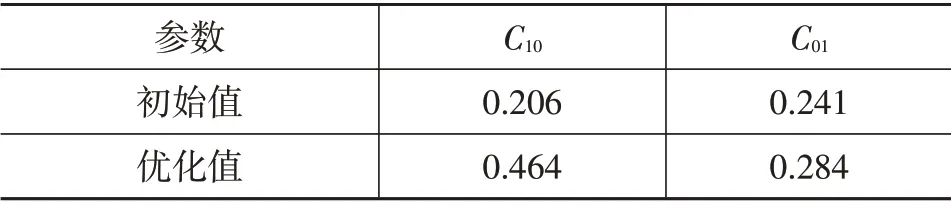
表6 Mooney-Rivlin模型优化参数

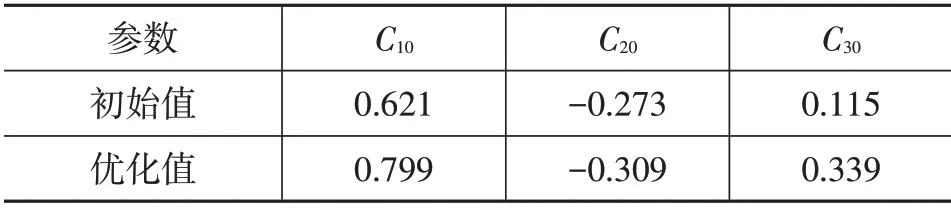
表7 Yeoh模型优化参数

3.4 优化结果验证

利用优化识别的参数重新计算橡胶衬套刚度，Mooney-Rivlin、Yeoh本构模型空心径向、实心径向和轴向刚度优化的结果分别如图10、图11所示。从图10、图11 中可以看出，基于优化的本构参数计算出的仿真刚度曲线更趋近实测刚度曲线，优化后的本构参数能描述衬套的宏观刚度特性。

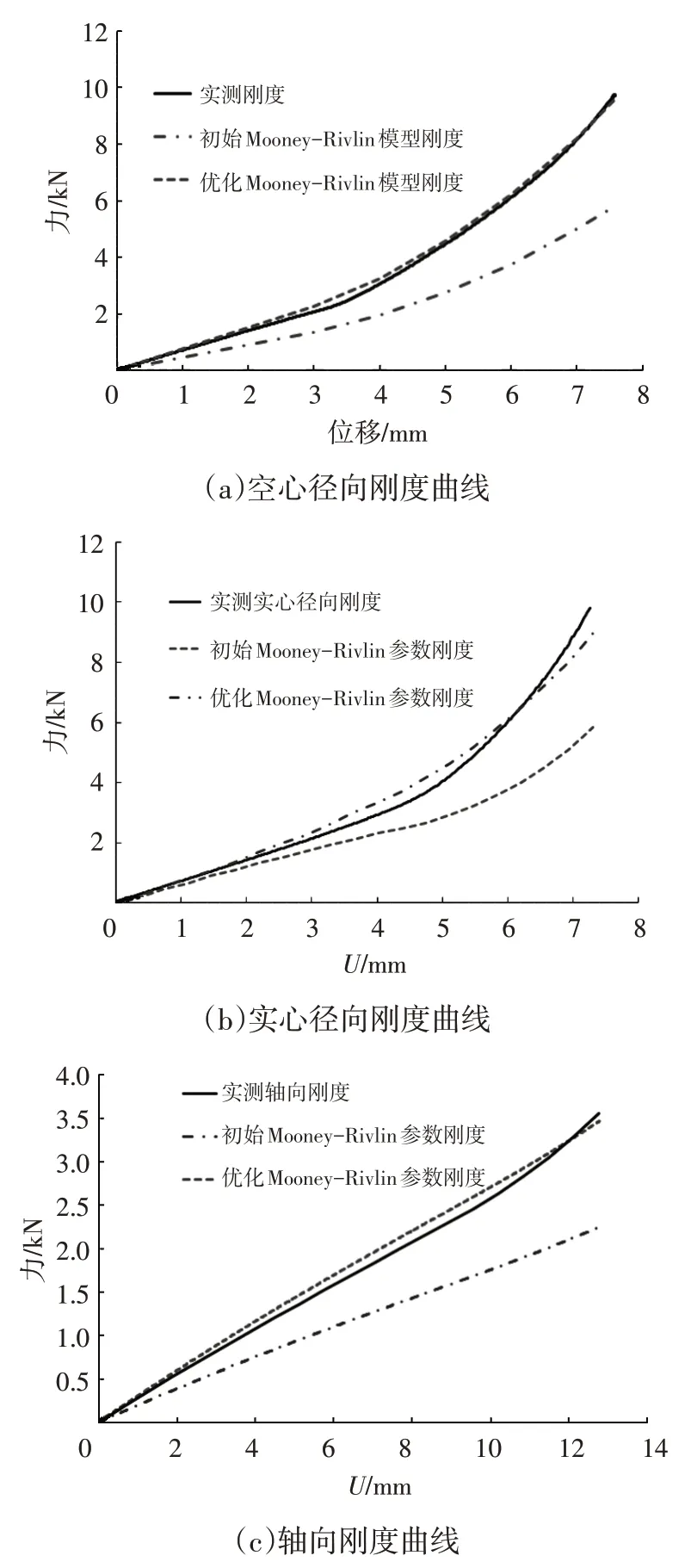
图10 Mooney-Rivlin模型优化结果

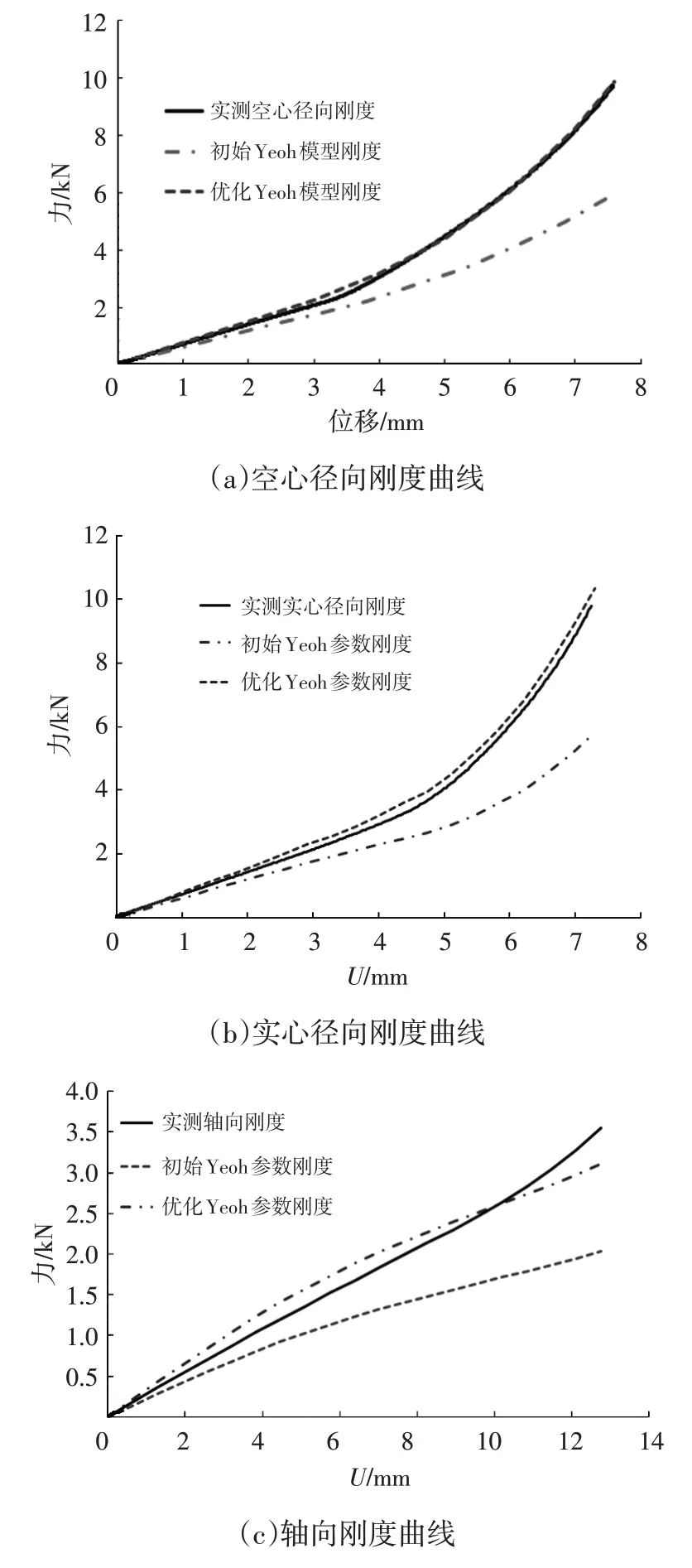
图11 Yeoh模型优化结果

需要指出的是，多目标优化并不总是能求解出优化解，影响因素主要有：

a.刚度大小趋势。当初始参数计算出的刚度与试验结果相比，在多个方向上表现为同步大或者小的情况时，比较容易优化出本构参数，但若某些方向刚度比试验结果大，而其余方向刚度比试验结果小，则很难优化出结果。

b.曲线形状。当初始参数计算出的刚度曲线与测试曲线形状相似、曲率相当时，较容易求出优化解，相反，如仿真刚度曲线初始线性段与试验曲线接近，而非线性段斜率较试验曲线大，则很难求得较优结果。

因此，要结合多种本构模型，利用初始参数，分别计算衬套的刚度特性，并根据以上2 点因素合理选择本构方程模型。本文算例应力应变分析有限元模型采用Yeoh 模型，由于其较好的非线性段表现，更适合求解大载荷问题，另外，其三段式参数能够更加灵活地控制刚度。

4 橡胶衬套寿命预测

通过前文的工作，可以获得方便仿真分析的块谱载荷和衬套超弹性本构参数，进而求得块谱载荷作用下的应变，在此基础上进行扭力梁衬套的寿命预测。

4.1 台架试验

根据路谱转化的块谱搭建三轴台架试验，如图12所示，整车x向载荷和y向载荷通过液压缸施加于衬套外套管，扭转角施加在衬套内套管，为了模拟实车行驶过程中衬套侧限位块与车身连接支架之间的撞击状态，试验夹具在衬套内套管上刚性连接了一个限位支架。

图12 橡胶衬套三轴台架试验

试验结束后发现衬套开裂，裂纹源为十字形衬套主筋拐角处，从结构上看，主筋为主要承载结构，该位置在承受挤压和扭转载荷时为优先破坏位置，试验循环14万次后开裂，如图13所示。

图13 橡胶衬套开裂位置

4.2 寿命仿真

参考台架试验边界条件建立有限元模型，如图14所示，衬套内套管和限位块定义为一个刚体，刚体控制点设置在旋转中心与套管轴线交点，x向载荷、y向载荷及绕y轴转角载荷均施加在刚体控制点上，约束施加在衬套外套管。

图14 橡胶衬套三轴台架仿真模型

疲劳寿命计算采用裂纹扩展法，橡胶材料损伤与幅值循环次数之间为非线性关系，以断裂力学理论表征为裂纹驱动力（撕裂能）和裂纹扩展速率之间的关系[12-15]，如图15所示。曲线描述了一个典型的裂纹驱动力与裂纹扩展率的关系模型，主要参数包括线性段斜率F、线性段与非线性段的过度点Tt、临界裂纹驱动力Tc和临界裂纹扩展率rc，当裂纹驱动力大于阈值T0时，开始产生裂纹扩展。寿命仿真设置初始裂纹值为0.1 mm，破坏裂纹尺寸设置为1.0 mm。

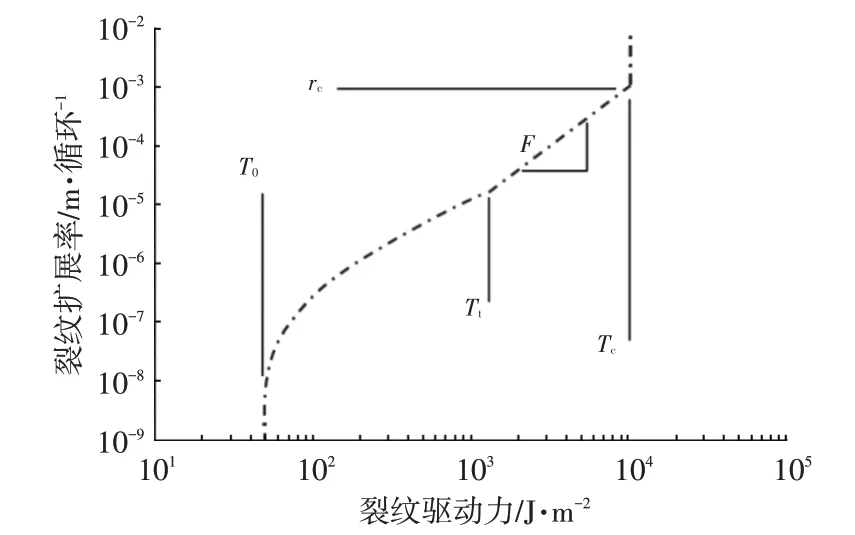
图15 Lake-Lindley裂纹扩展模型

计算各块谱的应力与应变时间步信息，叠加转化的循环次数，计算块谱载荷作用下橡胶衬套疲劳寿命，考虑载荷、材料、工艺等的离散性，疲劳损伤（Damage）目标设定为小于0.5。损伤分布如图16所示，最大损伤为0.634，不满足目标要求，最危险位置为主筋拐角处，与台架试验破坏位置一致。

图16 橡胶衬套疲劳寿命计算结果

4.3 方案优化

分析失效原因，主筋在衬套承载时起关键作用，故采用加宽主筋的方法进行优化，将主筋宽度由15.0 mm提高为18.5 mm，此优化产生的附带效应为径向刚度提升了23%，轴向刚度提升了12%。主筋加粗方案损伤值为0.221，如图17所示，疲劳损伤达到目标要求，寿命提高到约3倍。

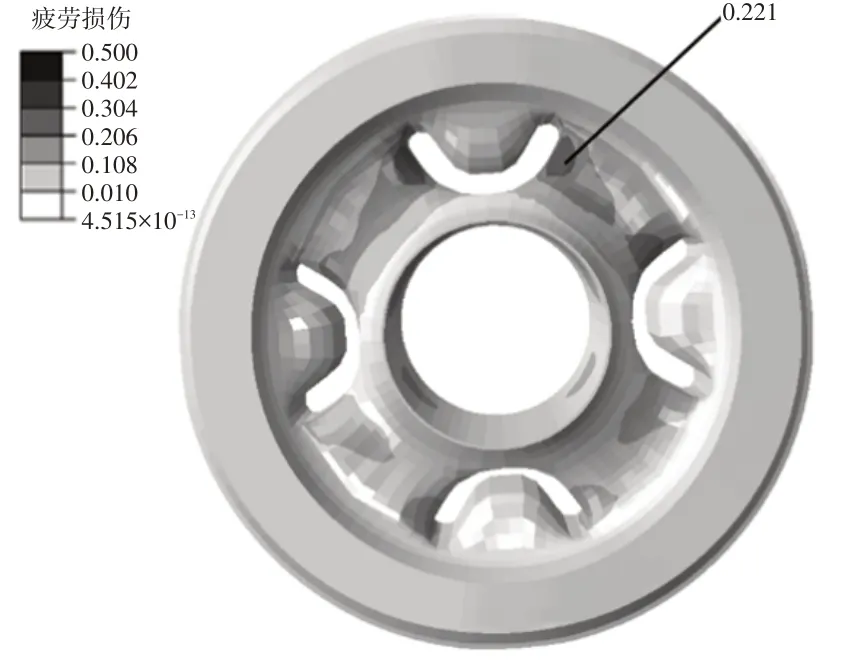
图17 橡胶衬套优化方案疲劳寿命计算结果

对优化后的橡胶衬套结构疲劳寿命进行台架试验验证，主筋加粗后台架试验寿命达到32万次，验证了疲劳寿命分析趋势的正确性，试验后的橡胶衬套如图18所示，满足试验目标要求。

图18 橡胶衬套优化方案台架试验结果

5 结束语

本文以扭力梁衬套为研究对象，探讨了衬套寿命预测中块谱转换和超弹性本构参数识别这2个关键问题，并对橡胶衬套的寿命进行了预测，危险点位置与台架试验结果吻合良好，并进行了方案改进，得到以下结论：

a.考虑到三轴耦合，载荷幅值、相位关系能覆盖原始路谱，衬套载荷谱转换方法可以用于橡胶衬套的寿命预测分析及台架疲劳试验；

b.在没有实际材料测试结果的情况下，利用已有的初始本构参数，结合有限元方法、参数优化方法，可以识别出能够较好模拟橡胶衬套静刚度特性的超弹性本构参数，以保证应变计算结果的有效性。

本文建立的基于路谱随机信号载荷的橡胶衬套寿命预测方法，系统地包含了橡胶衬套的载荷谱编制、超弹性本构参数识别、衬套寿命预测，为橡胶衬套耐久性问题解决提供了完整的方案，尤其是对于橡胶衬套超弹性本构参数的识别，可省略材料测试环节，简化了优化过程。