基于多尺度平稳小波分解的灰度遥感图像目标提取方法
回 征,周 诠
(西安空间无线电技术研究所,西安 710100)
0 引言
遥感[1]技术是指,通过使用不同传感器,在没有物理接触情况下,获取各类目标的光谱、物理等属性的信息和数据的技术。遥感图像在军/民用不同领域中有着重要作用。如何在海量遥感图像数据中准确有效地提取出重要目标,是遥感领域研究的一个重要方向。
主流的遥感图像目标区域提取方法,包括基于机器学习、基于深度学习以及基于视觉显著性检测的方法等。基于机器学习的目标检测方法[2-3]涉及大量统计学原理,可以通过分析数据统计出规律,并根据得出的规律进行相应目标提取。该类方法需要构造大量的目标模板,且需要先验知识才能提取目标,在资源受限的工程应用场合(如卫星遥感)中,尚存在一些问题。
近年来,人工智能领域出现了突破性的进展,随着各类深度神经网络的蓬勃发展,一些学者也开始探索将其应用于遥感图像的目标检测中[4-6],与传统的机器学习方法不同,使用基于深度学习的方法进行遥感图像目标提取能够自动地从图像中的标注目标学习特征,而不需要考虑人工构造和计算目标特征。此外,基于深度学习的方法拥有极高的检测准确率,也可以有效抵抗复杂的背景干扰。但是,这类方法搭建网络模型的过程十分繁琐,网络的训练也比较复杂,难以适应高实时性要求的应用场合,如航天器遥感等。
与上述两类方法不同,基于视觉显著性检测[7]的目标提取方法是一种不依赖人工标注样本进行网络训练的方法。人类视觉在观察自然场景时,大脑经过搜索可以在短时间内找到感兴趣的区域,并将更多的视神经计算资源分配给该区域,从而对目标进行更加高效的识别和判断。视觉显著性模型[8]正是通过建立数学模型,模拟人类上述视觉机制的方法。
根据显著性模型提取出的特征所属图像不同的域,视觉显著性模型可以分为空间域模型以及变换域模型。ITTI[9]模型是最具代表性的空间域模型,通过输入图像的色彩、强度以及方向通道使用不同尺度高斯滤波器,提取显著性特征,并提出一种“中心-周边差异”机制来融合计算显著性图。AIM(Attention-based on Information Maximization)模型[10]是另一种典型空间域,它从信息论的角度对人类视觉机制进行解释建模,从而构造显著性模型。Achanta等提出的模型[11]通过计算图像局部区域对比度,来构建输入图像显著性图,它改进了ITTI模型输出显著性图与原图像尺寸不同的缺陷。此外,典型空间域视觉显著性模型还包括GBVS(Graph-Based Visual Saliency)模型[12],CA(Context Aware)模型[13],LC(Local Contrast)模型[14],HC(Histogram Contrast)模型[15]等。空间域视觉显著性模型的物理意义不如频率域清晰,背景抑制能力较弱,且计算消耗较大。
Hou等[16]提出的SR(Spectrum Residual)模型是一种基于DFT视觉显著性模型,通过抑制图像频谱中低频部分来产生显著性图。由于相位谱在显著性图计算中起着更为重要的作用,Guo等在SR基础上放弃使用图像的幅度谱,提出了PFT(Phase Fourier Transform)[17],并通过对该描述子带进行IDCT变换分离出图像的显著性区域。Schauerte等在IS模型的基础上,将DCT模型替换为针对彩色图像的四元数傅里叶变换(Quaternion Fourier Transform,QFT)运算[19]。在Li等提出了超复数傅里叶变换(Hypercomplex Fourier Transform, HFT)[20]模型中,使用四元数对彩色图像的亮度以及CIELAB颜色空间上的色彩特征进行表示,随后通过四元数傅里叶变换得到图像在频率域的超复数表示,并通过多尺度高斯滤波来计算出的显著性图。
通过对现有视觉显著性模型进行研究和归纳,发现大多数视觉显著性模型都是针对彩色图像的空间域模型,其中的色彩特征是生成显著性图中不可缺少的参数,不适合直接应用于灰度图像;此外,空间域模型在计算上较为复杂,其显著性区域的物理特性也不如变换域模型清晰明了。而现有基于DFT和DCT的灰度图像视觉显著性模型,对于不同遥感图像和其中目标,其目标区域提取结果十分不稳定,准确率相差很大,提取出的目标区域也不够完整。
相较于DCT和DFT变换,小波变换拥有多分辨和时频域分析特性,其高频细节分量(水平、垂直和对角系数)可以表达输入图像的显著性信息,即一幅图像的目标(显著性)区域会与背景区域存在明显的特征差异,而这种差异则会在特定尺度的小波系数中凸显出来。平稳小波变换,在传统小波变换基础上略去了下采样操作,从而增加了冗余性和平移不变性,其细节分量保留的目标信息更为丰富。因此,本文提出一种基于平稳小波变换的变换域视觉显著性模型,用以进行灰度遥感图像中目标区域的提取。
1 本文方法
本文基于多分辨的平稳小波变换(Stationary Wavelet Transform,SWT)[21],提出一种目标区域的提取方法,算法流程如图1所示。
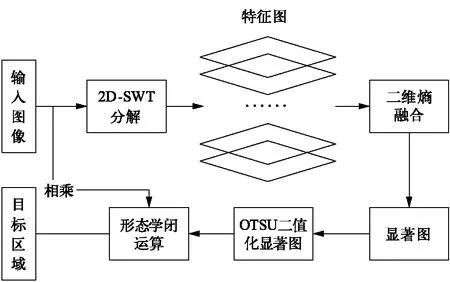
图1 本文算法流程
输入图像,经过不同尺度二维SWT分解之后,可得到一系列逼近系数,以及三个方向子带分量,使用所得的子带分量,可以重构出一系列特征图。由于SWT的冗余性,这些特征图的分辨率与输入图像相同。随后根据每一特征图的二维熵进行加权融合,得到显著性图。通过大津(OTSU)[22]算法分割对显著性图进行二值分割,最后通过形态学增强二值分割图,得到目标的二值轮廓。目标区域通过输入图像与二值轮廓相乘即可提取出来。
1.1 多尺度平稳小波分解
小波变换的高频细节分量(水平、垂直和对角系数)可以表达输入图像的显著性信息,一幅图像的目标(显著性)区域会与背景区域存在明显的特征差异,而这种差异则会在特定尺度的小波系数中凸显出来。因此在本文中,我们首先对输入图像进行K级的二维SWT分解,对于输入图像I,多级SWT分解如下:
(1)
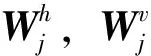
1.2 特征图计算
对于每一级分解得到的四个分量,使用N×N的全0矩阵A代替逼近分量Lj,利用逆平稳小波变换进行重构,得出该尺度下的特征图。随着分解级数的增加,可以得到一系列包含由粗到精图像结构的特征图,第j级ISWT重构特征图计算如下:
(2)
式中,ISWTj()为第j级逆平稳小波重构函数,Sj为特征图,η=104为一个约束因子。通过逐级对所得系数进行重构,一共可以得到K个特征图,相应地,由于SWT的冗余性,重构的特征图与输入图像分辨率相同。
1.3 基于二维熵融合的显著图计算
本节中,使用熵来计算显著图,是考虑到显著图的实质是一种概率分布。理想的显著图中,显著性(目标)区域的直方图应集中在几个有限的值处,而目标区域之外的值则应被有效地抑制。也就是说,当得到显著图的熵越小时,显著性区域就越凸显,对背景区域的抑制作用也就更强。
在传统信息论中,熵是一种统计量,无法提现出图像的结构特性。因此,需要对传统的熵定义加以改进。二维熵的定义如下:
H2D(x)=H{g*x}
(3)
式中,H为熵函数,g为高斯核函数,*为二维卷积运算。对每一幅特征图Sj,可得到其基于二维熵的加权系数wj
wj=(H2D(Sj*g))-1
(4)
得到加权系数后,对K幅特征图进行加权融合,得到显著性图
(5)
1.4 目标区域提取
在融合得到显著图后,本节采用OTSU(大津)算法对得到的显著图进行二值化处理。OTSU算法假定图像由前景色和背景色组成,通过计算选取最佳阈值,使得两者的类间方差最大,进而完成分割。对显著图进行OTSU分割后,显著性(目标)区域的像素值为1,而背景区域像素值为0。
对显著图进行OTSU粗分割后,得到的目标区域中含有较多的孤立点、空洞以及断裂,这里使用图像形态学闭运算对这些来填充这些离散孔洞以及分散部分,对于图像A以及结构体B,闭运算的定义如下:
A·B=(A⊕B)⊙B
(6)
式中,·为闭运算,⊕为膨胀运算,⊙为腐蚀运算。通过原图像与经过OTSU分割和闭运算处理后得到的二值掩模进行相乘运算,提取出最终目标区域。算法的大致流程如图2所示。

图2 基于显著性图的目标区域提取过程
2 实验结果及讨论
为了测试本文算法提取遥感图像目标的性能,本文在NWPU VHPR-10数据集中截取出6幅大小为512×512像素的灰度测试图像。此外,本文选取了3种经典的频域视觉显著性模型作为对比,包括基于DFT变换的SR算法,PFT算法以及基于DCT变换的IS算法,从主观视觉效果以及客观评价指标两个方面进行性能对比。
2.1 主观视觉效果
下面从人类视觉直觉角度上进行算法性能的对比,图3中(a)为输入原始图像。(b)~(e)分别展示了使用IS算法、PFT算法、SR算法和本文算法得到的显著图的直观视觉效果。为了能够抑制背景干扰,在不引入虚警目标的情况下,准确完整地分离出目标区域,所得到的显著图应具备以下特点:①目标(显著性)区域与背景区域具有较高的对比度,即目标区域保持均匀高亮;②与真实目标区域相比,显著图目标(显著性)区域应尽可能完整;③所得显著图中目标区域之外的错误目标应被有效抑制。
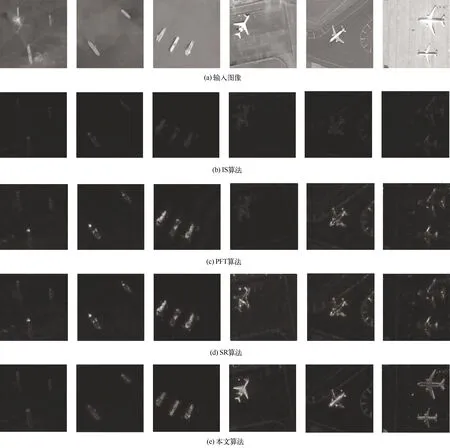
图3 不同算法显著性图的主观视觉效果
由图3可见,IS算法得到的显著图中,背景区域存在的干扰(如第一幅图中的云层以及第五幅图中机场跑道)可以被有效抑制,得到的目标区域也较为完整,但其对比度较低,所得到的显著性图中目标区域无法保持高亮。由SR和PFT算法得到的显著图效果较为类似,其中目标区域与背景区域的对比度较高,可以看出舰船及飞机目标的轮廓都能被有效标记出来,但其目标区域内部亮度不均,导致目标区域不够完整,此外一些干扰区域如云层和机场跑道也被错误标记为显著性区域。与其他三种算法得到的显著性图相比,使用本文算法得到的显著图,目标区域的亮度较高,与背景区域形成鲜明对比,标记的目标区域完整,区域内部亮度较为均匀,此外使用本文算法得到的显著性图对背景区域的干扰也起到有效的抑制作用。
为进一步对不同算法分离出的目标区域效果进行探究。使用手动标记的Ground-Truth图和四种算法分离出的二值轮廓图像进行对比。

图4 不同算法提取的目标二值轮廓对比
由子图像(b)~(e),我们不难看出,对于测试图像2、3,IS算法、PRT算法和SR算法提取出的目标区域较为完整,但是其他四幅图像,对比Ground-Truth图像,有着下列问题:①目标区域不完整,远小于原目标(图像1);②引入了检测错误的干扰背景(图像1、4、5);③检测的目标切片破碎,完整度较低(图像6)。相比之下,使用本文算法提取的舰船、飞机目标,形状最接近于Ground-Truth图像中的目标,背景干扰被有效地抑制(云层以及机场跑道)。此外我们可以观察到,在四类算法中,使用本算法提取出的目标亮度最为均匀,形状完整度最高。
2.2 准确度客观评价
在本节中,我们选取了查准率P(Precision)[23]、查全率R(Recall)[23]以及F度量[23]值Fβ对相关算法提取目标的准确度进行评价,实验中遥感图像的真实目标Ground-Truth记为G,提取出的目标区域记为T。
查准率P和查全率R是目标检测领域的重要评价指标,Precision指的是正确提取的目标区域面积|G∩T|与提取的目标区域面积|T|之比,Recall指的是正确提取的目标区域面积|G∩T|与Ground-truth图中目标区域面积|G|的比值,其具体定义如下:
(7)
(8)
Recall和Precision的取值范围都为[0,1],其取值越靠近1性能越好。但是,二者不能孤立的讨论,后续又有学者提出F度量值Fβ对提取的目标区域性能进行综合评价。
在2.2节中,我们提到对于N×N大小的输入图像,其最大SWT分解级数为J=log2N,而本文算法需要一个最大分解级数K≤J,来计算得出K幅特征图,图5展示的是不同分解级数K下测试图像的F度量值曲线。
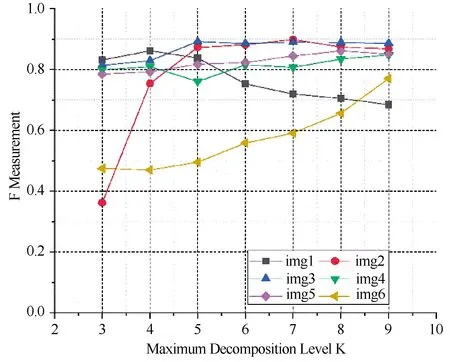
图5 不同K值下测试图像的F度量曲线
由图5可以看出,不同的测试图像,其目标区域提取综合准去度F度量值受最大SWT分解级数K影响,通过选取合适的K值,测试图像的F度量可以在0.85以上。在前文中分析过,K值越高,得到的特征图就会引入更多输入原图像的细节信息,对于包含更多背景区域干扰的图像,选取较低的K值,所得的特征图含有较少的细节分量,可以有效抑制面积较小的背景区域干扰。而对包含较少背景干扰区域的图像,选取较高的K值,可有效增加显著性图中目标区域的对比度,提取出更完整清晰的背景区域。
对6幅测试图像,使用IS算法、PFT算法、SR算法和本算法进行目标区域提取,并对照手工标记的Ground-Truth图像,计算得出一系列的Recall、Precision以及F度量,得出的柱状图如下。
由图6的Recall和Precision柱状图可以看出,对于6幅测试图像,本算法得到的Recall和Precision值集中在0.75~0.8之间,而基于DFT的SR算法和PFT算法,对于其中一部分测试图像,出现了Recall值接近于1而Precision值只有0.25~0.4的情况,这是因为使用这两种算法提取出的目标区域过大,混入了过多不属于真正目标的背景区域,使得面积|G∩T|≈|G|而|G∩T|=|T|,出现了很多检测错误的目标。而根据子图(c)计算出来的F度量柱形图,可以发现本文算法的综合目标提取准确度,并没有随图像的不同而产生变化,同时使用本文算法得到的F度量也明显高于其他三类算法。

图6 不同视觉显著性模型的目标提取客观评价指标
综上所述,在主观视觉上,相较于其他三类经典频域视觉显著性算法,使用本算法提取出的目标区域在视觉上形状与输入原图像目标更为接近,提取出的目标更为清晰完整,且能够一定程度抑制背景区域干扰。在客观评价标准上,本文算法的Recall值和Precision值相对稳定,可达到0.85以上,而综合Recall和Precision值计算出的F度量,也处于四种算法中的领先地位,具有更好的目标区域提取准确性。
3 结论
目标区域提取是遥感图像处理的一大重要研究方向。基于机器学习和深度学习的目标提取方法,具有良好的性能,但对样本需求较高,且网络训练较为复杂,在资源受限的工程应用场中不宜发挥其性能优势。而视觉显著性检测,不需要额外的样本进行训练,具有较低的运算复杂性,较好契合资源受限的应用场合。本文提出了一种针对灰度遥感图像的基于多尺度平稳小波分解的目标区域提取算法。现阶段通过视觉显著性计算来提取目标区域的大多数算法,都需要图像的色彩特征,针对灰度图像的算法较少。此外,基于DFT和DCT的视觉显著性模型,提取的目标区域的准确率,很大程度依赖于输入图像,随不同图像性能变换很大。本文针对这一系列问题,利用多尺度平稳小波分解,使用细节分量构造特征图,并根据不同特征图的二值熵进行加权,融合出显著性图。最后通过OTSU分割以及形态学处理,得到目标的二值轮廓完成目标区域提取。实验证明,本文的目标分割效果在主观客观上都取得较好效果。

