基于手机信令数据的城市轨道交通线网建设时序决策支持模型*

刘思涵 林诗佳 张竹君 钮心毅 LIU Sihan, LIN Shijia, ZHANG Zhujun, NIU Xinyi

0 引言

随着我国城市人口规模不断扩大，出行需求持续增长，各大城市大力发展公共交通尤其是大运量城市轨道交通来缓解交通问题。2019年，全国已有40个城市的轨道交通正式运营，总运营里程达6 736.2 km[1]。北京、上海、广州、深圳等城市的城市轨道交通系统早已成网，苏州、杭州等城市也即将进入成网阶段，城市轨道交通规划的重点由单线规划转向网络规划。城市轨道交通线路建设是一项长期、高成本的系统工程，线网规划不合理带来的影响将会难以调整。国务院近年出台的《关于进一步加强城市轨道交通规划建设管理的意见》等建设意见[2-4]多次强调建设时序的科学合理性，提出“以人为本、统筹协调、因地制宜”等原则，明确要根据城市实际情况，充分论证城市轨道交通建设的必要性，合理确定建设时序。

目前已有的关注城市轨道交通建设时序的研究提出了若干定性和定量研究框架。陈婉等定性分析了城市轨道交通建设时序的影响因素，认为贯穿城市轨道交通建设近期、中期、远期和建设、运营、管理的共同影响因素是交通需求、线网完备性以及与城市空间发展的协调性[5]。但定性分析往往主观性较强，实际应用中需要定量分析的支撑。一些研究使用定量分析方法，从空间区位、线网等级、经济效益、工程实施等方面出发，建立城市轨道交通建设时序的决策方法。如从城市总体规划或城市轨道交通专项规划出发，将线网分为骨干网、发展网、辅助网，结合规划中的功能分区，选取线网节点并计算其重要度，根据线网等级和区位确定城市轨道交通的建设时序[6-7]。也有研究从经济效益出发，考虑建设资金控制，或通过建立城市轨道交通项目的全寿命周期费用模型和待建线路的预期收益模型，将经济效益最好的线路作为优先建设的线路[8-9]。另有研究考虑了多个因素，包括线路长度、工程实施难度、日客运周转量等，使用专家打分法、层次分析法（analytic hierarchy process, AHP）或熵值法求出多个影响城市轨道交通建设时序的评价指标权重并建立模型，用以确定城市轨道交通的建设时序[10-12]。

已有方法多关注静态物质层面要素，将城市规划或交通规划的蓝图作为指标选取和评价的重要依据，忽视了乘客的活动规律和需求。在城市轨道交通进入网络化建设时期后，精确把握客流预测是城市轨道交通规划、建设以及运营最大的困惑和难点之一[13]。城市轨道交通已经开展建设但尚未成网的阶段，各个站点的实际客流和服务范围可能会有较大差异，反映出城市不同地区对城市轨道交通的不同需求。目前对城市轨道交通客流的监测主要停留在已有线网内部以及站点之间的客流上，如各站点客流量、客流站间交通起止点（origin and destination,OD）等，难以获知乘客在城市轨道交通线网以外的活动轨迹，无法准确地探知站点的服务范围和服务对象。

随着移动通信的全面普及和移动设备数量的增加，手机信令数据成为研究人群时空行为特征的一大方法[14]。本文使用手机信令数据识别城市轨道交通乘客及其站外全程活动轨迹，基于实际客流的出行分布建立城市轨道交通线网建设时序的评估决策模型。在完成城市轨道交通线网规划的基础上，为短期内的线网建设时序提供决策支持。

1 研究方法

1.1 总体框架

模型遵循建构—检验—预测三步。其中，模型的建构包括三个内容，即测度站点服务、量化乘客需求、评估线路服务。与此对应，融合大数据方法与传统交通模型，形成研究框架。首先，改进传统交通模型，计算站点的理论服务范围，测度站点的服务能力；其次，基于手机信令数据识别乘客出行轨迹与站外OD分布，通过溢出理论服务范围的乘客在空间上的出行分布，量化测度乘客的实际需求未被现有线网服务满足的部分；最后，建立量化评价体系，基于乘客空间分布的溢出程度评估线路建设迫切程度，为精准判读拟建线路的建设优先级提供直观有效的量化参考。建构完成以上城市轨道交通建设时序的决策支持模型后，通过杭州市实证案例数据对模型的参数选取和结果进行检验、预测和应用（图1）。

图1 研究框架Fig. 1 research framework

1.2 城市轨道交通理论服务范围

国内外许多学者对城市轨道交通站点的服务范围做了较深入的研究，基本可概括为四类：基于经典TOD理论预设固定范围、基于问卷调查建立模型测算服务范围、基于开发利益角度测算服务范围以及基于出行时间模型测算服务范围。其中，基于出行时间模型测算服务范围的方法以乘客的出行需求为依据，与乘客实际时空轨迹有对比意义，且相较于问卷调查的方法，推广性更强。本文借用基于时间可达性一致的等效路阻模型测度城市轨道交通站点的理论服务范围。该模型以时间成本最优为导向，认为在站点的影响范围边缘步行到站点后搭乘城市轨道交通到城市中心的时间与直接搭乘公交巴士出行的时间相同，即在此范围内城市轨道交通相比于其他公共交通方式有更强的吸引力。这一模型最早由张小松等提出，用于测算城市轨道交通站点的开发利益影响范围[15]。之后武倩楠等针对城市居民出行并非全部以市中心为目的地这一现实情况，划分交通小区并引入城市轨道交通可达点概念，用于精细化测算站点的接驳范围[16]。

本文在此方法的基础上，使用互联网地图更精准地读取公共交通的服务线路、运行速度与时间，用于划定站点理论服务范围。

1.3 基于手机信令的城市轨道交通乘客识别

近年来，有一些学者将手机信令数据用于分析站点的服务范围，但部分研究受数据和方法限制，只能通过间接方法推测手机用户是否为城市轨道交通乘客[17-18]，识别出的乘客误差较大，因此这种方法所描述的乘客在地面的活动轨迹与实际情况有较大偏差。根据乘客进入城市轨道交通地下站点会强制进行位置区码（location area code , LAC）切换的原理，可以准确识别城市轨道交通乘客，并进一步根据地上轨迹来判断乘客的来源和去向，以此来测算站点的服务范围。这一方法利用手机信令数据原理直接识别城市轨道交通乘客，准确度较高，通过对比城市轨道交通刷卡数据发现二者各站点的平均相对误差仅有8.9%，且可以将乘客地上和地下的活动连接起来，准确计算其在地面的活动轨迹，以判断站点的实际服务范围[19-20]。

在上述方法基础上，通过路测得到地铁站点的LAC编码表，用以识别手机用户的进出站行为，进而识别出手机用户中的城市轨道交通乘客；将乘客的地上、地下行为连接成为完整的出行链，可以计算出乘客在地面的出行轨迹和数量在空间上的分布，并将其作为站点的实际服务范围；将乘客实际分布与站点理论服务范围叠加，得到溢出乘客数量与分布，为下一步评价体系的建立提供基础。

1.4 建设时序决策评分

溢出乘客作为空间数据，其数值分布和空间分布是两个基础属性，为此采用数量、出行距离、来源地方向三个特征量化描述和评价溢出乘客。总溢出距离指标由站点的溢出乘客数和溢出乘客的出行距离共同决定，表征了站点乘客溢出的强度和广度。信息熵最初由克劳德·艾尔伍德·香农（Claude Elwood Shannon）提出，用以度量随机变量的不确定度。信息熵在众多领域都得到了应用且被证实有意义。在城市规划领域，信息熵被用于衡量城市土地利用的均衡性[21]和城市人口密度分布的均衡性[22]，能够量化分析城市轨道交通站点的客流来源方向分布的均衡性。最终使用统计学方法，将总溢出距离和信息熵两个指标的中位数作为参照，构建建设时序决策评分坐标系，对拟建线路进行综合评分，并根据得分高低判断建设时序。

2 模型构建

根据上述研究框架将模型主体分为三个子模型。子模型1基于改进的传统交通模型计算站点理论服务范围；子模型2基于手机信令数据测算站点实际服务范围；子模型3基于客源溢出构建建设时序的量化评价体系（图2）。

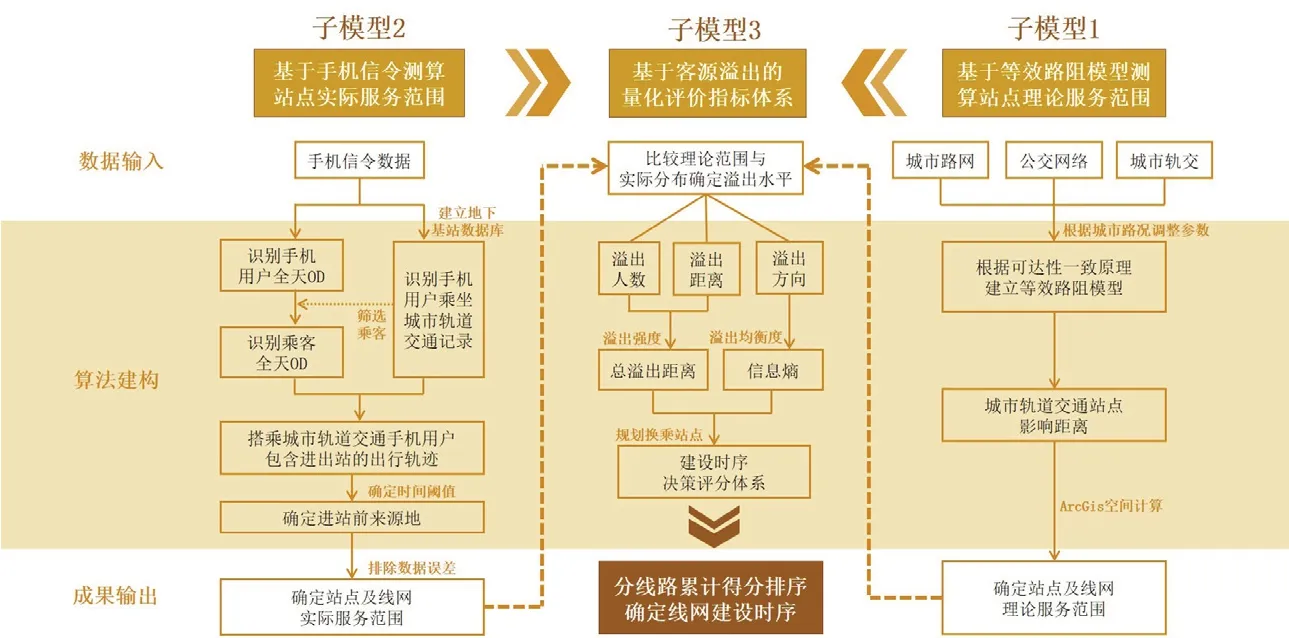
图2 模型流程Fig. 2 model process

2.1 基于等效路阻模型测算站点理论服务范围

子模型1对基于时间可达性一致的等效路阻模型进行了改进。该模型首先需要根据研究城市的实际情况划定城市中心车站和市郊区边界。前者是计算时间可达性的空间参照，后者考虑到公交巴士的路面行驶速度受路况影响，通常认为市中心车辆行驶速度低于郊区。其次，计算城市轨道交通按照运营线路从各个站点到达城市中心的车程距离和公交巴士按照线路从各个站点到达城市中心的车程距离，其中公交车程分为市中心线路距离和郊区线路距离。最后根据城市交通实况，估算城市轨道交通的平均旅行速度，公共汽车在市区的平均旅行速度、公共汽车在郊区的平均旅行速度和乘客从城市轨道交通影响范围边缘点到车站出行的平均速度。将上述变量带入公式1，可以求得各个站点的影响距离，以站点为圆心、相应影响距离为半径做圆，即可得出站点的理论服务范围（图3）。

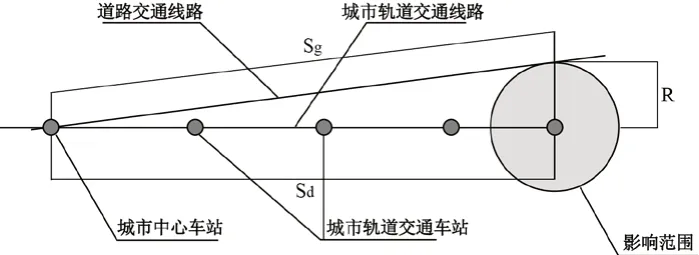
图3 基于时间可达性一致的等效路阻模型Fig. 3 equivalent traffic impedance model based on time accessibility

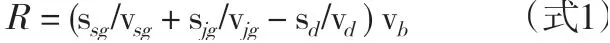
传统方法一般使用ArcGIS构建道路网络数据集完成上述步骤，交通工具的运行速度通常是根据经验取值，不能完全反映城市的真实交通情况。为此，改用百度地图开放应用程序接口（application programming interface, API），运用互联网地图计算出最佳公共交通路径和用时，作为各类交通工具站点间的距离和速度。该方法考虑到了地方性和差异性，计算出的出行路径更贴近乘客实际出行选择，交通工具速度的估算也更贴近各个城市的实际路况，结果更真实可信。

2.2 基于手机信令测算站点实际服务范围

子模型2基于手机信令数据，采用以“最大距离、最大时间”为核心思想的经典出行链算法，即通过设置信令间隔时间和距离两个阈值，计算得到所有手机用户全天OD出行表。使用由路测得到的城市轨道交通地下站点LAC表筛选出信令记录中包括站点LAC的手机用户，即城市轨道交通乘客；进而通过地上、地下LAC切换的信令识别出乘客进站、出站的站点和时间，得到站间OD表。根据时间顺序连接乘客的地面OD与站间OD，得到乘客包含地上地下出行行为的完整出行链。合并逻辑可以划分为包含和顺序两类关系，其中顺序关系根据时间先后又可细分为两种（图4）。

图4 基于城市轨道交通地下站点地铁乘客出行链识别进站前来源地Fig. 4 identify the origin of subway urban rail transit underground station passengers based on the travel chain

得到乘客完整OD表后，以“进站前一小时内停止空间移动、并连续停留大于半小时”为阈值，筛选出乘客进站前的来源地基站。将来源地基站与站点距离大小累计前85%作为筛选条件，选取最终列入计算的乘客来源地基站，并做核密度分析，推算乘客的分布，并将其作为各城市轨道交通站点的实际服务范围。其中，进站前一小时内停止移动排除了超长距离出行的干扰并考虑了线路末端站点乘客的出行特征；连续停留大于半小时排除了地面换乘行为对于停留地判断的干扰；基站与站点距离前85%的范围能够排除非常规出行行为和少量数据误差带来的数据分布尾部影响。

2.3 基于客源溢出的建设时序决策评价体系

子模型3首先将子模型1和子模型2的结果叠加，找出实际乘客来源范围超出理论服务范围的溢出乘客，再借助总溢出距离指标和信息熵指标，共同构建基于客源溢出的建设时序决策评价体系。

使用总溢出距离指标表征站点溢出乘客的数量和来源距离。公式为：

其中，Dp为站点总溢出距离，N(Gi)为溢出乘客数，D(Gi)为溢出乘客来源距离。该指标基于各站点的溢出乘客分布核密度图，使用核密度栅格中心与站点的直线距离作为溢出乘客的来源距离，栅格的核密度值乘以栅格面积作为溢出乘客数。计算各栅格溢出乘客数和乘客来源距离的乘积，累加得到站点的总溢出距离，综合反映站点的实际乘客溢出强度。总溢出距离越大，站点实际乘客溢出强度越大。

使用信息熵指标量化评价站点实际溢出乘客的方向分布均衡性。公式为：

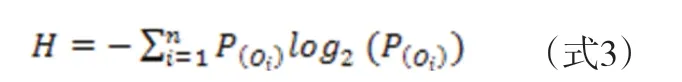
其中，H为站点溢出乘客分布的信息熵，P(oi)为站点Oi方向溢出乘客数占站点总溢出乘客数的比例。该指标将站点周边分为n个方向，统计核密度栅格中心落入各个方向的栅格，其核密度值乘以栅格面积之和作为各方向溢出乘客数，计算各方向的乘客数占所有方向总溢出乘客数的比例。该指标用于表征站点溢出乘客在各方向分布的均衡性。信息熵越小，溢出乘客分布越不均衡，信息熵越大，分布越均衡。当所有溢出乘客均来自同一方向时，信息熵取到最小值-log2(1)=0；当所有溢出乘客均衡地分布于各个方向时，信息熵取到最大值log2(n)。

将上述两个指标用于评价城市轨道交通站点客源溢出的强度和均衡度，表明城市轨道交通现有供需情况的失衡，将其用于构建建设时序决策评分体系，可以得到基于真实客源需求的建设时序决策支持方案。

将总溢出距离指标作为横轴，信息熵指标作为纵轴，取所有评价对象站点的两个指标的中位数作为零点，构建评分坐标系。坐标系的四个象限代表不同的供需不匹配度。位于第四象限的站点表示不均衡强溢出，位于第一象限的站点表示均衡强溢出，位于第三象限的站点表示不均衡弱溢出，位于第二象限的站点表示均衡弱溢出（图5）。根据规划站点总溢出距离和信息熵两个指标的散点图落入的象限计算得分。将一条拟建线路与已建成线路的所有换乘站及其上下两站得分加和，得到线路总得分，作为建设时序决策评分体系的输出结果。该模型输出的线路总得分越高，该线路对于现状服务溢出改善程度就越高，因此建设时序越靠前。

图5 建设时序决策评分体系Fig. 5 construction sequence decision scoring system

3 模型检验与预测

3.1 案例概况

选取2017年杭州市七区（西湖区、拱墅区、江干区、下城区、上城区、滨江区、余杭区）的城市轨道交通线网作为模型检验的研究对象。2017年4月，杭州市城市轨道交通共有1、2、4号线3条线路投入运营，共50个地下站点，包括4个两线换乘站点。使用2017年4月和7月的连续两个工作日的手机信令数据，对应杭州市2号线钱江路站以西的西北段开通前后的情况。由于2号线西北段为2017年7月3日开通，故7月的数据增加了该段的9个地下站点，共59个地下站点。2017年4、7月恰好是杭州城市轨道交通仍未成网时期，且4、7两个月份的数据也代表了一条新线路（2号线西段）开通前后的乘客活动特征，因此适合用本模型检验。

拟建线路的候选方案，是根据杭州市总体规划中的城市轨道交通系统规划，选取近期建设且与现状线网联系紧密的7条拟建线路作为评估对象（图6）。首先将4月数据输入模型进行运算，得到建设时序预测结果，再利用杭州市7月实际建设情况和7月数据的模型运算结果检验模型结果可靠性和指标有效性，并证实模型可进行迭代预测。

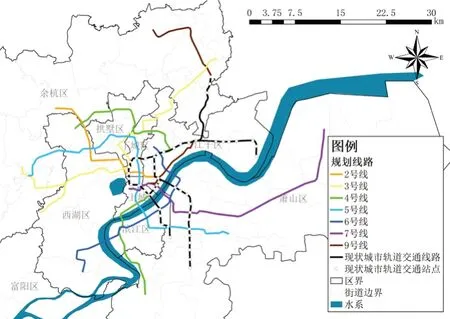
图6 选取的拟建线路Fig. 6 selected planned rail transit line

3.2 案例模型构建

基于杭州市的实际情况，子模型1选取位于市中心的换乘站凤起路站作为市中心站点，选取杭州市机动车限行边界作为划分市中心和郊区的边界。通过百度地图开放API，估算出杭州市公共汽车平均行驶速度市区段为15 km/h、郊区段为25 km/h，城市轨道交通平均行驶速度为35 km/h，人平均步行速度为5 km/h，选取时间最短路径计算各交通工具的行驶距离，代入式1计算得到各站点基于等效路阻模型的影响范围。其中，考虑到城市中心区其他公共交通线路密集的情况，发现通过模型测得的城市轨道交通站点影响距离偏小，因此根据相关研究，位于中心区的影响距离小于500 m的站点的理论服务范围均以500 m计算。

通过路测，获得杭州市59个地下轨道交通站点的LAC编码表，用于子模型2识别手机用户中的地下轨道交通乘客。

基于杭州市手机基站密度与研究尺度，子模型3选取核密度栅格像元大小为100 m×100 m，计算总溢出距离指标时，栅格的面积为10 000 m2。计算信息熵指标时，本次案例研究将每个城市轨道交通站点周边的360°平均划分为16个方向，每个方向为以站点为端点、夹角为22.5°的两条射线所包含的区域。信息熵指标表征了站点的溢出客流在16个方向分布的均衡性。

3.3 杭州市4、7月份模型结果与实证检验

将子模型1计算出的杭州市50个地下站点的理论服务范围通过ArcGIS做缓冲区进行可视化，横向比较可以发现站点服务范围存在端部效应，即线网端部站点的影响范围较大、中间站点的影响范围较小（图7）。

图7 杭州市4月份溢出乘客分布Fig. 7 distribution of overflow passengers in Hangzhou in April

使用子模型2通过2017年4月份手机信令数据识别平均一日内杭州市城市轨道交通乘客39.6万人次，所有乘客进站前来源地与站点的人均距离为1.51 km，其中有15.5万人次进站前的来源地位于其站点理论服务范围之外，占所有乘客的39.12%。从空间分布上看，乘客来源高值区在主城区西、北方向呈现出连绵成片溢出的现象，尤其是第一高值区呈向西的线性延伸趋势（图7）。

将上述步骤识别出的溢出乘客核密度数据作为输入数据输入子模型3。通过总溢出距离和信息熵两个指标的空间分布可以发现，市中心西北侧和线路末端站点均有服务溢出强度高且分布不均衡的特点，这种不均衡的强溢出表示城市轨道交通线网在这些区域的服务能力缺失（图8）。对案例中的7条拟建线路进行全线路累计得分计算，4月份模型结果中得分最高的为5号线，建设时序应最靠前。然而在实际项目的实施过程中，全段线路通常会安排分期建设。因此按照不同方向对各线路进行分段，该模型还可以用于模拟实际分期建设的时序。模型分段结果表明，杭州市4月份建设时序最靠前的应为2号线西段、4号线北向段、5号线江西段和9号线南段（图9）。

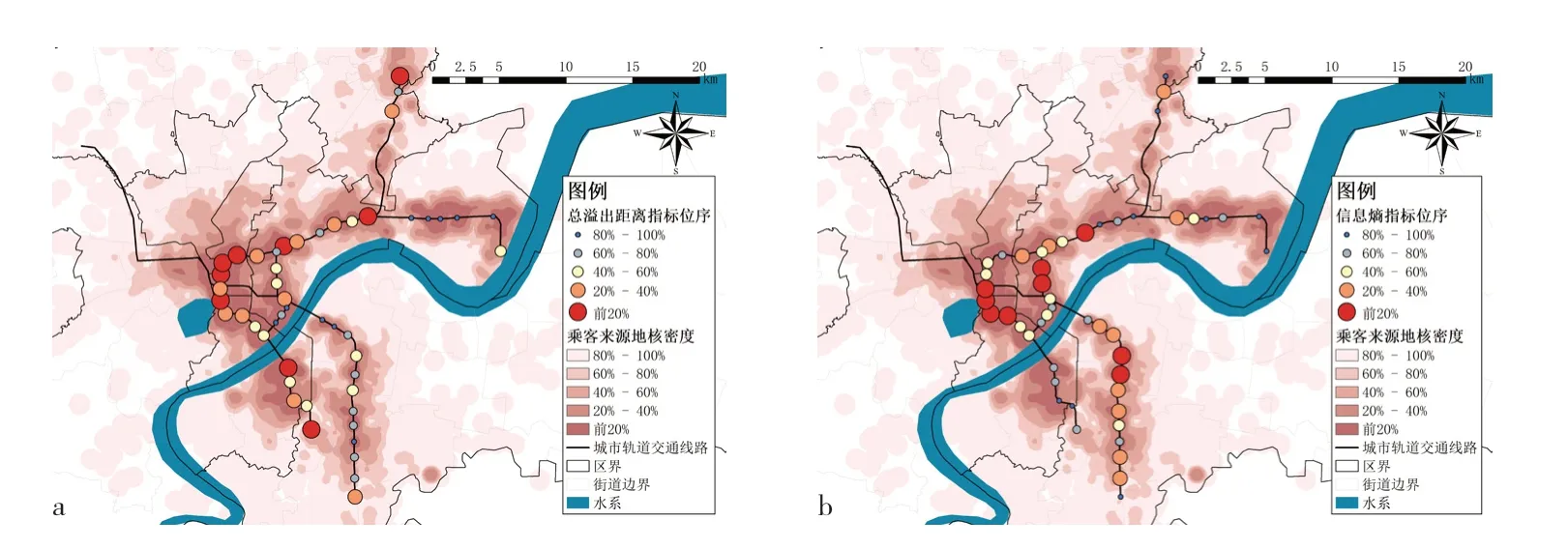
图8 杭州市4月份总溢出距离指标（a）和信息熵指标（b）Fig. 8 the total overflow distance index and information entropy index of Hangzhou in April

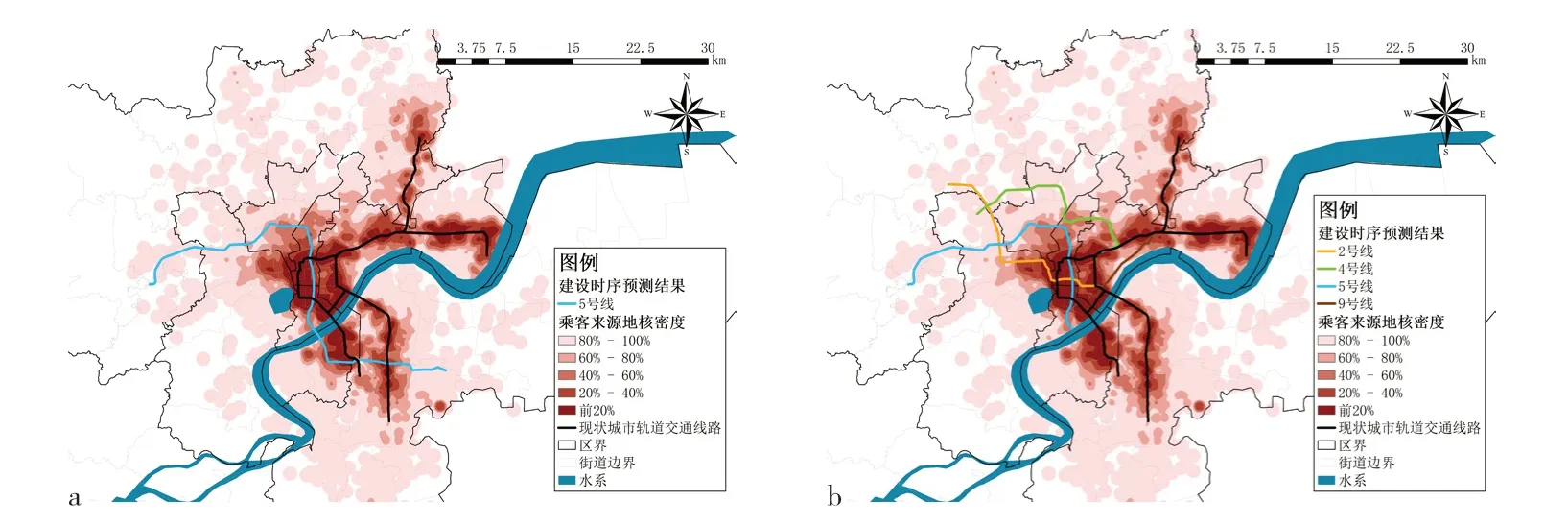
图9 杭州市4月份全线路预测结果（a）和分段预测结果（b）Fig. 9 the full line predicted result and the segment predicted result in Hangzhou in April

在杭州市城市轨道交通建设实践中，2017年7月实际开通了2号线西段，与模型分段预测结果一致，因此认为模型的结果具有可信度。在城市轨道交通建设实际时序决策中，还受到用地批复、建设成本等多因素影响，本模型从乘客实际需求出发，提出城市轨道交通建设时序决策支持，经过实践验证是有效的。

将杭州市7月份2号线西段开通后的数据输入模型，识别乘客37万人次，所有乘客进站前来源地与站点的人均距离为1.42 km，其中有13.4万人次进站前的来源地位于其站点理论服务范围之外，占所有乘客的36.15%。与4月份手机信令识别的结果对比，新线路建成后，杭州市城市轨道交通乘客平均来源距离减小，溢出乘客数也减少。进一步观察总溢出距离指标和信息熵指标的变化情况（图10），与2号线西段建成前相比，线路建成后新线路周边站点的总溢出距离指标均有所减小，信息熵指标均有所增大，即站点的溢出强度与均衡度均得到了一定改善，说明新线路的建成能够缓解附近原有站点的服务溢出情况，选取总溢出距离指标和信息熵指标能较好地指征站点的服务溢出情况。

图10 杭州市4、7月份总溢出距离指标变化（a）和信息熵指标变化（b）Fig. 10 changes of overflow distance index and information entropy index in Hangzhou between April and July

4 结 语

4.1 结论

研究建立了基于实际客流活动轨迹的城市轨道交通线网建设时序决策支持模型。子模型1针对计算站点服务能力的需求，改良了基于时间可达性一致的等效路阻模型，考虑了城市中交通工具的运行效率和乘客的出行选择，并将其应用于理论服务范围的测算。子模型2针对一般手机信令数据无法识别客流真实时空活动的难点，使用手机信令数据和地下站点的LAC数据，能够准确地将乘客从手机用户中剥离出来，从而识别乘客的完整出行轨迹。研究提出了可靠的识别算法和经过实践检验的参数取值，测算出站点的实际服务范围。子模型3从供需不匹配出发，将溢出乘客的数量、来源距离、方向分布进行量化，构建了一套完整的评估指标体系。

模型集成了大数据方法与传统交通模型，相比传统的建设时序决策方法，解决了乘客来源地探知这一难题，扩展了交通评估和规划决策的数据源和相应分析方法。

通过杭州市两个月份的手机信令数据和城市轨道交通建设实践，实践案例验证了模型的参数选取和指标的有效性，模型的结果通过了实证的检验。模型整体经过了构建、检验和模拟三个阶段，增强了实用性和可靠度。

4.2 讨论与展望

4.2.1模型的适用范围

基于乘客来源地分布的方法，模型适用于成网阶段前的短期城市轨道交通线网建设时序的决策。城市轨道交通线网规划是一个复杂的工作，需要考虑城市空间结构、土地开发、人口分布、工作岗位分布、客流量、经济成本等因素。已经编制完成的城市轨道交通线网规划是较长时期内城市轨道交通线网建设的指导。然而实践中，在规划的诸多线路中还需要进一步挑选近期优先建设的线路。尤其是在骨干线路已经建成、即将步入网络化的阶段，乘客的实际需求在建设时序决策中尤为重要。城市轨道交通线网越完善，乘客来源地的分布就越均衡且接近于站点的理论服务范围，因此模型的适用性可能会下降。

4.2.2模型的改良

由子模型1改进的等效路阻模型目前仅考虑了常规公交巴士的竞争，且在乘客从出发点到城市轨道交通站点时默认选择步行。目前我国城市共享单车、共享汽车等新型公共交通发展蓬勃，对乘客出行路径的选择和交通时耗都有影响。考虑进一步将多种交通方式与城市轨道交通进行对比，并考虑不同类型的接驳方式将是本模型的改进方向。

子模型2利用手机信令识别城市轨道交通乘客地面来源的方法仅适用于地下站点。由于利用地下站点LAC切换原理的识别方法尚无法识别出地上站点进出的乘客，因此还无法对城市轨道交通的地上站点进行评价和预测。

4.2.3模型的应用场景

模型可用于不同城市的城市轨道交通线网建设时序的决策。其中，由于子模型2集成了大数据方法框架，可以将其应用于城市轨道交通客流时空动态监测、管控与预测。子模型3的评分系统是基于对城市轨道交通站点现状服务能力的评价，因此也可应用于交通设施服务评价。模型整体基于城市轨道交通实际服务的乘客轨迹预测建设时序，由于城市轨道交通对城市空间结构与功能格局的重要作用[23-24]，因此在实际规划建设中还要考虑城市各方面的发展需要，在模型预测结果的基础上做进一步决策。