基于主动禁忌搜索的稀疏码多址接入技术低复杂度检测算法

彭小洹，赖 恪，潘志鹏,雷 菁

(国防科技大学 电子科学学院，湖南 长沙 410073)

0 引言

第六代移动通信(6G)已经展开了研究,与5G相比，6G具有更高的频谱效率和更大的系统容量。传统的正交多址技术(Orthogonal Multiple Access,OMA)已经无法满足需求[1-3]，非正交多址接入技术(Non-Orthogonal Multiple Access,NOMA)通过在发送端允许多用户共享相同的时频空资源，在接收端进行多用户检测，能有效地提高系统吞吐量和接入用户数，被认为是未来6G系统的关键技术之一[4-5]。

一般而言，NOMA技术可以分为功率域NOMA(Power-Domain NOMA,PD-NOMA)以及码域NOMA(Code-Domain NOMA,CD-NOMA)两大类[6-7]，而本文所探讨的稀疏码多址接入(Sparse Code Multiple Access,SCMA)正是CD-NOMA方案的典型代表。SCMA最早由Nikopour等人在低密度签名(Low Density Signature,LDS)基础上提出[8]。在 SCMA 中，对比特进行 QAM 调制和扩频的两个步骤由一个码书映射步骤所代替，这一过程中比特被直接映射成为复数域的多维符号。 SCMA 用户的码书是指该用户比特对应的多维稀疏符号向量的集合。作为区分，不同的用户拥有各自独特的码书，利用码书设计过程中多维星座的成型增益，SCMA 可以获得相比 LDS 更佳的性能[9]。

SCMA检测算法是 SCMA 技术的核心。 Hoshyar 等人最早提出使用 MPA 算法来对稀疏结构的 LDS 系统进行多用户检测，获得了近似 ML 的优异检测性能[10]，这一方法被直接移植到 SCMA 的检测中。 MPA 算法的基本思想是通过外消息在系统抽象出来的稀疏因子图的变量节点和校验节点之间迭代传递，收敛得到一个用于判定符号的概率值。虽然 SCMA 技术通过码字在频域的稀疏扩展可以极大地降低 MPA 算法的计算复杂度，但是其实现复杂度仍然非常高，尤其在复用的用户数df较大和调制阶数M较高时， MPA 的复杂度会呈指数增加。具体而言， MPA检测复杂度为O(TMdf)，其中T表示算法迭代次数。因此，设计创新的算法和结构来降低计算成本成为后续研究 SCMA 的学者们的主要方向之一。

为了降低SCMA接收机的复杂度，一般从码本大小、迭代次数、行重因子以及每次迭代参与点数四方面入手。文献[11-12]提出了一系列扩展对数域Max-Log (Extended Max-Log,EML)算法，基本思想是根据其对置信度参与迭代的符号进行截断，从而降低参与每轮迭代的符号个数。为了使MPA可以以更快的速度收敛，文献[13]提出了一种基于串行更新的消息传递算法。该算法能够在当前迭代中立即传播已更新的消息，从而加快收敛速度，减小迭代次数，达到降低复杂度的目的。另外，从降低行重的角度来看，文献[14]提出了一种基于边选择的消息传递算法(Edge Selected MPA,ES-MPA)，该算法利用接收端已知的信道状态信息，只选择信道质量较好的部分边来更新从资源节点到用户节点的消息，而剩下的边所传递的信息则是利用高斯近似的方法来计算。同时，为了补偿信息损失，更新高斯模型的均值作为反馈，从而保证在降低复杂度的同时几乎不损失误码性能。为了降低MPA的搜索空间，文献[12]提出了一种基于动态阈值的消息传递算法(Dynamic Threshold-based MPA,DT based-MPA)，该算法的核心思想是为在不同的信噪比下挑选不同数量叠加星座点参与资源节点迭代更新过程。另外，文献[15]提出了一种基于列表球形解码(List Sphere Decoding,LSD)的消息传递算法，该算法只在给定半径的超球面内搜索出候选列表集，然后将此列表集中的点参与资源节点更新的迭代过程，由此降低了复杂度，但该算法的半径不能依据高斯噪声动态变化。可以看到，目前多数的SCMA译码算法均是基于MPA进行简化的。为此，本文引入主动禁忌搜索算法[16-17]，从而规避了MPA的使用，相较于传统的基于MPA的简化算法，本文所提算法具有如下优势：① 本文所提算法具有参数调整灵活的特点；② 本文所提算法不依赖于MPA，可以大幅度降低SCMA的检测复杂度，同时获得良好的性能。

1 SCMA信号模型

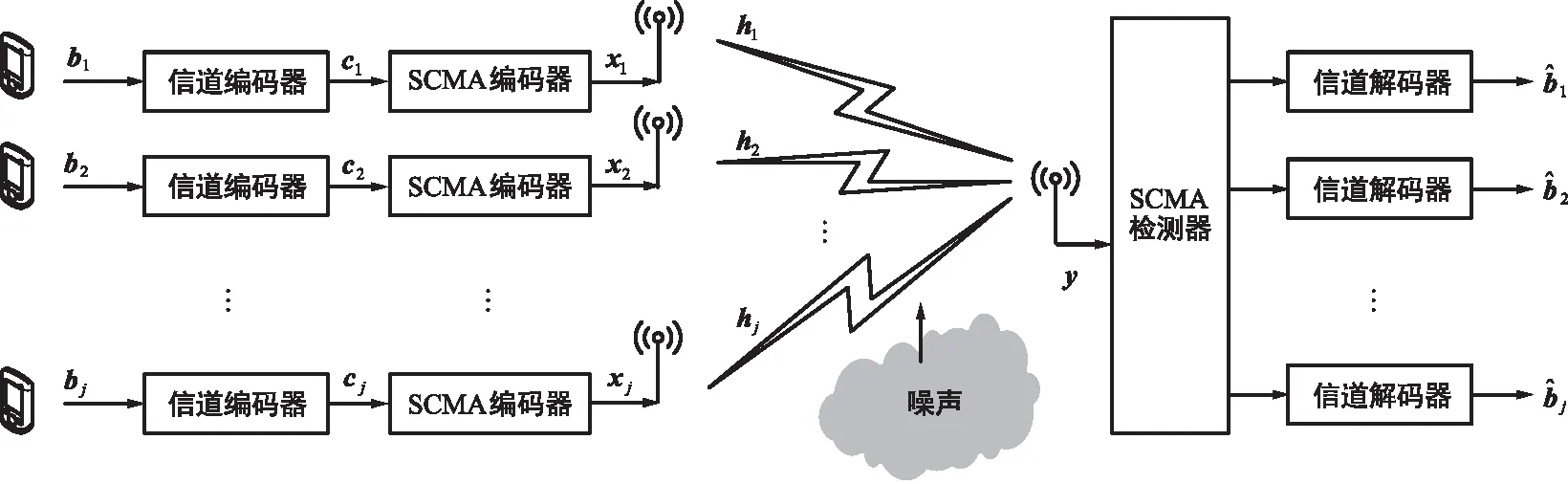
图1 典型SCMA系统框图Fig.1 System model of conventional SCMA

在经过 SCMA 编码器后，不同用户的稀疏码字便会映射到K个物理资源(如 OFDM 子载波)上。假设接收信号为y=[y0,y1,…,yK-1]T，信道增益hk=[h0,k,h1,k,…,hK-1,k]T，以及噪声向量v=[v0,v1,…,vK-1]T。接收信号是所有用户经过各自信道后叠加而成的，可以写成

(1)

(2)

从式(2)可以看出，在一个物理资源上，每一个用户j都会受到来自其他J-1个用户的干扰。

类似于 LDPC 码， SCMA 码字的低密度结构也可以用因子图来有效刻画。用一个长度为K的二进制列向量fj中的“0”和“1”来分别表示用户j的码书中零元素和非零元素的位置。那么，用户和资源之间的关系就可以用一个K×J的稀疏的因子图矩阵F=[f1,f2,…,fJ]来表示[18]。

(3)

式中，F的行表示资源，列表示用户。例如F中的第k行j列个元素fk,j，表示第j个用户在第k个资源上传输数据。

2 基于主动禁忌搜索的SCMA检测算法

2.1 主动禁忌搜索

禁忌搜索(Tabu Search，TS)最早由美国工程院院士 Glover 教授在 1989 年提出，它是一种全局优化算法，一经提出就受到广泛关注，并陆续在组合优化、生产调度以及机器学习等诸多领域获得成功的应用。之后，Glover、 Faigle 等学者针对禁忌搜索的收敛性展开了一系列数学上的理论研究。同时，还有许多学者针对禁忌搜索性能和效率的平衡问题展开了一些算法的实际应用和改进研究。

TS的基本思想是迭代地从当前解移动到其相邻的解。与其他启发式搜索算法不同的是，TS算法加入了禁忌列表，其限制了已经出现的解在有限的禁忌周期T内不能再作为下一次移动的对象，从而保证了搜索解的多样性，使其能够跳出局部最优解，更容易获得全局最优。然而，简单的 TS 算法在实际使用中主要有以下3点要求难以满足：① 根据不同的任务确定合适的禁忌周期T；② 算法参数对于不同问题求解的鲁棒性；③ 采用最小计算复杂度的算法来搜索历史状态。为此，学界提出了主动TS(Reactive TS,RTS)以解决上述问题。

在 RTS 中，禁忌周期T能够在搜索过程中通过相应的反馈机制来动态决定。具体而言，算法起始时T=1，当有明显表征显示需要增加解的多样性(Diversification)时使T增加，而当这种表征消失时则减小以增加解的集中性。一般而言，是否需要多样性的表征，可以用当前访问的解状态出现的重复次数来衡量。RTS在搜索过程中所有的历史搜索状态都会被存储下来。算法每执行一步，就会检查当前解状态在之前搜索中是否出现过，出现的频率如何，然后据此来决定T是增加还是减小。

因此， RTS 的禁忌周期在搜索过程中不是固定的，而是根据搜索空间的局部结构来动态决定的。对于一个“非均匀”搜索空间(指搜索空间中不同区域的统计性质有较大差异)而言，固定禁忌周期显然不再合适，此时 RTS 更适合解决此类问题。

2.2 基于主动禁忌搜索的SCMA检测算法

SCMA多用户检测器的目标在于利用y和H的先验知识估计出。根据 ML准则，有

(4)

式中，γ(X)=XHHHHX-2R(yHHX)定义为 ML 代价函数。

步骤一：初始化参数

令g(m)为m次迭代后得到的最优解向量，lreq为相邻两个重复解向量之间的平均步长(或者迭代次数)。P为最大禁忌周期，表示如果在一次迭代中某一移动被标记为禁忌状态(即禁忌列表中对应元素为P)，则在未来的P次迭代内，该移动会一直保持禁忌状态。二元标志位lflag∈{0, 1}用来指示算法在当前迭代是否达到了局部最优，主要应用于算法的终止准则中。

算法开始前需要通过 MMSE 等方法获得初始解向量x(0)，然后设置g(0)=x(0),lreq= 0,P=P0，禁忌矩阵T中元素全部置零。同时，分别计算yMF≜HHy和R≜HHH。

步骤二：邻域搜索

初始化lflag= 0，为方便表达，定义f(m)≜Rx(m)-yMF，e=z(m)(u,v)-x(m)。则对于给定解向量x(m)，其所有dvJN个邻域向量z(m)(u,v),u=1,2，…,dvJ,v=1,2，…,N的 ML 代价函数可以计算如下

φ(z(m)(u,v))=(x(m)+e)HR(x(m)+e)-2R((x(m)+e)HyMF)=

φ(x(m))+2R(eHRx(m))+eHRe-2R(eHyMF)=

φ(x(m))+2R(eH(Rx(m)-yMF))+eHRe=

φ(x(m))+2R(eHf(m))+eHRe=

(5)

(u1,v1)=argminu,v(u,v)。

(6)

目前为止，所求的最佳移动(u1,v1)能否执行，还需要依赖其实际 ML 代价值以及相应的禁忌状态。只有满足如下任意两个条件之一，则表示上述移动是被允许的。

γ(z(m)(u1,v1))<γ(g(m)),

(7)

T((u1-1)M+q,v1)=0,

(8)

若条件(7)和(8)均无法满足，则意味着移动(u1,v1)应该处于禁忌状态并且不满足特赦条件。此时，算法根据等效 ML 函数寻找次优移动，即

(9)

然后,再次对移动(u2,v2)进行条件(7)和(8)的判断。若仍然判断为禁忌状态，则继续次优(u3,v3)，直至找到满足上述条件的移动。当发现所有dvJN个移动均标记为了禁忌状态，则将禁忌表中所有元素减去它们的最小值，总会有一个移动的禁忌值为 0。令(u′,v′)为满足条件的有最小等效 ML 代价的移动，则求得的相应的解向量为：

x(m+1)=z(m)(u′,v′)。

(10)

注意式(5)最后一行，表示x(m+1)的获得可以迭代地求得γ(z(m+1)(u,z))，进而开始下一轮迭代。

步骤三：检查解的重复次数，动态改变禁忌周期

对步骤二所得解向量进行重复性分析。方法是通过比对该解向量的 ML 代价值与历史搜索解向量的 ML 代价列表，找出最近出现的重复解向量并更新平均重复距离lrep，同时调整禁忌周期P=P+ 1。若禁忌周期P已经有lp>βlrep,β>0次迭代没有发生改变，则令P=max(1,P-1)。同时，若γ(x(m+1))<γ(g(m))，则

T((u′-1)M+q′,v′)=T((u′-1)M+q″,v″)=0，

(11)

g(m+1)=x(m+1)，

(12)

否则，

T((u′-1)M+q′,v′)=T((u′-1)M+q″,v″)=P+1，

(13)

lflag =1,g(m+1)=g(m)。

(14)

该步骤根据解向量的重复频率，动态改变禁忌周期P，恰好体现出算法“主动禁忌”的含义。

步骤四：更新禁忌矩阵

更新禁忌矩阵中所有移动的禁忌值，即

T(r,s) = max{T(r,s) - 1, 0}，

(15)

式中，r=1,2,…,dvJM,s=1,2,…,N。同时,

(16)

式中,Ru′是指矩阵R的第u′列。若步骤四中的终止条件未被触发，则算法重复步骤二～步骤四，直至满足算法终止条件。

步骤五：算法终止准则

结合信号模型和调试经验，给出如下3个算法终止条件。只要满足3个条件任意一个则终止算法，输出最终解向量：

① (搜索步长条件)当搜索步长(即迭代次数)超过算法设定最大迭代次数Tmax时，算法终止；

② ( ML 代价条件)当算法获得的当前最优解向量g(m)的 ML 代价值γ(x)满足

γ(g(m))<Θi，

(17)

式中，Θi为设定的算法阈值，且lflag=1时，算法终止。算法阈值根据经验可进一步定义为：

(18)

式中，σ2为噪声功率，ri为阈值控制参数；

③ (解向量重复条件)若当前搜索获得的最优解向量的重复频率R达到设定的最大重复频率Rrep时，算法终止。

算法的具体流程如图2所示。

图2 SCMA-RTS 检测算法流程图Fig.2 Flow chart of SCMA-RTS detection algorithm

2.3 基于外迭代禁忌搜索的SCMA检测算法

在实际应用中，单纯地由某一初始解向量出发，进行单次 RTS 搜索难以在算法性能和复杂度之间取得较好的平衡。一方面，算法对于初始解向量的取值十分敏感，若取值不合适，即使采用了禁忌准则， RTS 也需要经历较长的搜索路径才能找到最佳解向量，此时算法复杂度甚至高于 MPA 检测;另一方面，单次 RTS 搜索在较高信噪比时，十分容易出现误码平层。基于上述两方面考虑，在 SCMA-RTS的基础上进一步提出基于外迭代的 RTS 检测算法，其基本思想是通过选取不同的初始向量进行多次 RTS 搜索，以拓宽 RTS 搜索区域、提升检测性能，同时通过合适的迭代退出条件来保证算法复杂度。

IRTS算法主体仍然是 RTS，不同之处在于在外围加入了循环迭代机制。通过相应的初始向量选取方法得到搜索起始向量后， IRTS 开始进行 RTS 运算，并得到该次搜索的最佳解向量。此时，算法判断解向量是否满足外迭代退出条件。如果满足，则输出相应的解向量作为最后输出结果；否则，再次生成一个不同的初始向量进行 RTS 搜索，重复此操作直至满足外迭代退出条件。

3 仿真结果及分析

作为启发式算法， RTS 和 IRTS 涉及的参数对算法 BER 和复杂度性能有重要影响。本节对所提出的 RTS 和 IRTS 检测算法进行仿真验证，考察其误码率和复杂度性能，并给出了算法相关参数的敏感性分析，相关的仿真参数如表1所示。

表1 仿真参数

3.1 误码率与复杂度对比

选取如表1所示的基准参数，对 RTS 和 IRTS 两种算法的BER性能和复杂度进行仿真分析，其结果如图 3和图 4所示。

由图 3可以看出， RTS 相比 Log-MPA有大约2 dB的性能损失。并且随着信噪比的增大，其BER 开始出现误码平层,其原因在于随着信噪比的增加，基于 ML 代价值的搜索空间中局部最优解的数量大量增加，而考虑到复杂度的影响，所以无法使用更长的搜索路径来避免所有的局部最优。通过分析如表2所示的不同信噪比下平均搜索步长Ti的值,可以得出一致的结论。可以看到随着信噪比的增加，所需要的Ti也随之增加，与之对应地，BER 曲线随之下降。但是到Eb/N0= 14 dB 后，Ti的值由于算法结构和参数的限制不再增大，由此导致算法 BER 曲线开始偏离原来的趋势，而出现误码平层。对应到复杂度曲线，这一现象则是在高信噪比区域复杂度系数收敛的原因。值得注意的是，即使随着信噪比增加复杂度有所增加，但是其加法操作数和乘法操作数最大仍然分别只有 Log-MPA 的 10% 和 30%。这一比例在低信噪比时更低。

而IRTS在提高RTS检测性能的同时，较好地解决了误码平层的问题。从图中可以看出， IRTS 相比 Log-MPA 仅有 0.5 dB 左右的性能损失，相比 RTS 有 1.5 dB左右的性能提升，同时消除了误码平层。背后的原理在于外迭代机制的引入，使得算法能够在信噪比较高时，选择若干个初始解向量开始搜索，搜索区域变大，因而克服了原本从单一初始向量出发陷入循环的问题。从表3可以看出， IRTS 在相同信噪比下的内迭代次数相比 RTS 略有减少，而外迭代次数随信噪比增加呈现先增加后减小的趋势。这是阈值参数选取和算法结构共同导致的结果。另一方面，基于随机干扰的 IRTS 也由于外迭代的引入带来了额外的复杂度。相比 RTS， IRTS所需的加法和乘法操作数几乎是 RTS 的3倍，但是仍然远低于 Log-MPA。相比其他低复杂度算法， RTS/IRTS 主要有以下优点：① 算法参数鲁棒性高，对不同信道、不同规模码书的 SCMA 系统均能够有较好的检测性能；② 通过阈值控制参数ri和ro， IRTS 可以方便地根据需要来选择更低的复杂度或者更加优异的性能；③ 没有 MPA 算法中指数型复杂度阶数，因而在处理M或者df较大的 SCMA 系统时，更具有复杂度上的优势。

图3 RTS 和 IRTS 的 BER 性能Fig.3 BER performance comparison between RTS and IRTS

图4 RTS 和 IRTS 的复杂度性能Fig.4 Computational complexity comparison between RTS and IRTS

表2 RTS 在不同信噪比下的平均搜索步长

表3 IRTS 在不同信噪比下的平均搜索步长

3.2 参数敏感性分析

3.2.1 RTS参数敏感性分析

本节针对不同参数对于RTS以及IRTS算法BER性能的影响进行敏感性分析。

如图 5所示，在信噪比较低时，算法对于最大搜索步长有良好的鲁棒性，其 BER性能基本不发生变化。而在Eb/N0≥ 12 dB 时，随着Timax的增大， BER 性能将随之改善,但相应地，复杂度也随之增加。这是因为随着信噪比的提高，更宽松的搜索步长限制能够使 RTS 有可能以更长的搜索路径为代价找到全局最优解。同时，注意到Timax≥70时， BER曲线基本趋于平缓，这是因为随着搜索过程的进行，其他终止条件开始起主要作用。基于此可选择Timax=70作为基准参数值。

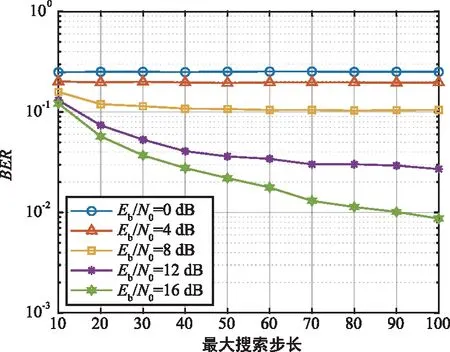
图5 Timax对 BER 的影响Fig.5 Impact of Timax on BER

图 6展示了不同信噪比下，内阈值控制参数ri对算法 BER 和复杂度性能的影响。从图中可以看出，随着ri的增加，算法 BER 性能恶化明显；相反地，复杂度系数却大幅下降。这是因为RTS 算法 ML 代价终止条件指出，当所得解的 ML 代价值小于内阈值时即终止搜索。而ri的增加即内阈值Θi的增大，意味着放宽了上述 ML 终止条件，使得部分ML 代价值较大的局部最优解被当做全局最优解输出，从而导致性能变差。同时，宽松的终止条件也导致了更短的搜索步长，因而其算法复杂度也随之下降。

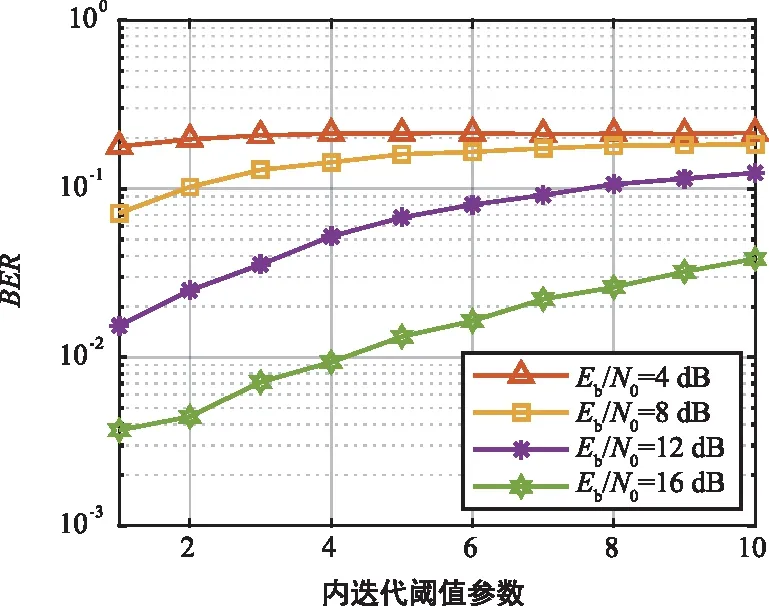
图6 ri对 BER 的影响Fig.6 Impact of ri on BER

3.2.2 IRTS参数敏感性分析

图 7展示了不同信噪比下Tomax对算法 BER 和复杂度系数的影响，可以看出，在Tomax≤4时，随着Tomax增加， BER 性能随之改善，而复杂度也随之明显增大。注意到，当Tomax=4时， BER 性能基本达到收敛，而相应的复杂度也相对稳定。因此，可以选取Tomax=4作为最大外迭代次数参数基准值。

图7 IRTS 中Tomax对 BER 的影响Fig.7 Impact of Tomax on BER in IRTS

IRTS通过对历史解向量施加一定维度di的随机干扰，使得算法能够在充分利用历史搜索信息的基础上，尽可能地跳出当前局部搜索区域，以获得全局最优解。图8展示了不同信噪比下di对于算法 BER的影响，可以看出，随着干扰维度的增加， BER 性能略微改善。这是因为干扰维度的增加，意味着有更大几率跳出当前解的搜索范围，而更广的搜索范围将获得更优的检测性能。因此，选取干扰维度di=4作为基准参数比较合适，此时算法 BER 性能较好、复杂度较低。

图8 di对 BER 的影响Fig.8 Impact of di on BER in IRTS

4 结束语

本文提出一类基于主动禁忌搜索思想的 SCMA 检测算法，包括 RTS 和 IRTS。RTS 检测算法是一种全局性邻域搜索算法，它通过引入禁忌表，并且设置规则动态地改变每个历史界的禁忌周期，保证了搜索解的多样性，使其能够跳出局部最优解，更容易获得全局最优。 SCMA 的 RTS 检测算法大体包括初始化参数、邻域搜索、检测解的重复次数、更新禁忌矩阵和判断算法终止条件等5个步骤。而实践中发现，单次 RTS 搜索尽管能够取得极低的检测复杂度，但是 BER 性能损失较大。

为此，本文在 RTS 检测算法的基础上继续提出了基于外迭代的 RTS 检测算法(IRTS)，将单次 RTS 搜索作为内迭代，然后引入外迭代机制来进行多次 RTS 搜索。采用基于随机干扰的初始向量选取策略，使得算法既能够拓宽搜索区域、提升检测性能，也能够充分利用历史搜索信息。仿真结果表明，通过合适的参数选取， RTS 能够以 2 dB 左右的 BER损失，带来只有 Log-MPA 操作数 10% 左右的低操作复杂度。而 IRTS 则通过引入外迭代，解决了 RTS 中误码平层的问题。虽然其复杂度相比 RTS 有所增加，但性能显著提升，相比 Log-MPA 只有 0.5 dB 左右的损失。同时，通过恰当的参数选取，RTS 和 IRTS 可以方便地调节复杂度性能和 BER 性能，具有相当的应用场景适应性。