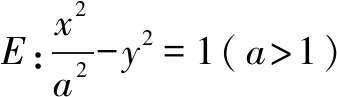2020年全国Ⅰ卷理科解析几何第20题的剖析与探究
杨伟达
(广东省广州市花都区第二中学 510800)
一、题目再现

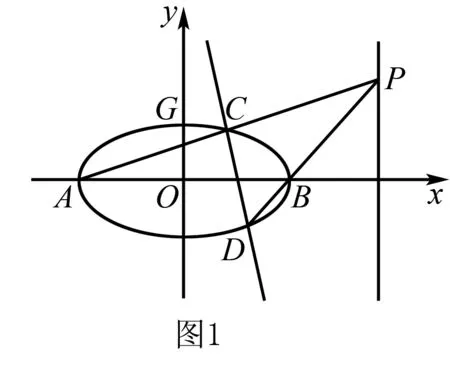
(1)求E的方程;(2)证明:直线CD过定点.
考点分析试题分为两问,第(1)问注重基础,以向量的数量积为工具,结合椭圆性质求椭圆方程,难度较小;第(2)问考查直线与椭圆位置关系、一元二次方程、韦达定理、直线方程,突出对数学核心素养的考查.从思想方法和数学素养层面看,本题考查了函数与方程、转化与化归、数形结合、逻辑推理及处理复杂表达式的运算求解等.
二、思路探究及解答过程
1.思路探究
(1)尝试用自己的语言表述题目的已知条件、结论、未知量是什么
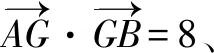
(2)常见相关类型题目及解题思路
有关直线与圆锥曲线相交问题常见的方法是联立方程组,利用方程组求解.
(3)思维障碍
本题涉及三条直线,与椭圆相交需要联立方程组,消元转化为一元二次方程,方法简单自然,但涉及运算量较大,不少学生渴望而不可求.
(4)思路分析
第(1)问:b=1,由椭圆的性质及向量数量积可列方程求出a的值;第(2)问:设直线AP和直线BP分别与椭圆相交,求出CD的直线方程,从而判断直线CD恒过定点.
2.解答过程
解法1 (联立方程组+韦达定理)
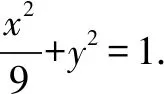
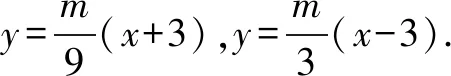
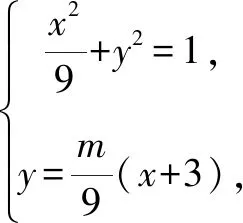







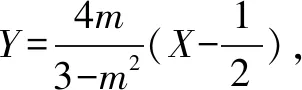
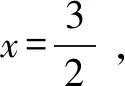
综合比对,求解方法一样,只是将椭圆问题变成圆的问题,图形变得简单,运算量也变小,但是要进行伸缩转换,还原求值,仅供参考.
三、解题后反思
1.不变的通性通法,突显核心素养
首先,全方位考查直线方程.不管是从点到线还是从线到点,离不开直线与椭圆相交,在涉及过点M求直线方程时常常“缺什么设什么”.即缺少斜率,在斜率存在时不妨设斜率为k,所以直线方程为y-y0=k(x-x0).
再次,直线与圆锥曲线的交点问题常常联立方程组转化为一元二次方程、判别式、韦达定理等.这种“独木桥”式的通性通法在高考中屡见不鲜.特别是消元和运算求解方面要求更高.总之,考查学生运算求解素养依然是高中数学重点考查的素养之一,也是高考突显选拔、分层功能的重要体现.
2.变更条件、编写题组

变式2 已知A,B分别为圆E:x2+y2=1与x轴的左、右交点,点P为直线x=m(m>1)上的动点,PA与E的另一交点为C,PB与E的另一交点为D.证明:直线CD过定点.