Exact solution of an integrable quantum spin chain with competing interactions∗

Jian Wang(王健) Yi Qiao(乔艺) Junpeng Cao(曹俊鹏) and Wen-Li Yang(杨文力)

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

4Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China

5Institute of Modern Physics,Northwest University,Xi’an 710127,China

6Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China 7School of Physics,Northwest University,Xi’an 710127,China

Keywords: quantum spin chain,Bethe ansatz,Yang-Baxter equation

1. Introduction

Quantum magnetism is an important issue in research of condensed matter physics. Spin-spin interactions can induce many interesting phenomena such as novel magnetic ordered states, fractional spin excitations and quantum phase transitions. The typical spin-spin interactions include the nearest neighbor(NN),next nearest neighbor(NNN),Dzyloshinsky-Moriya(DM)interactions and chirality three-spin couplings.

Focusing on the NN interaction, the most famous model is the Heisenberg model. It is well-known that the elementary excitation of the isotropic Heisenberg model is gapless while that of the anisotropic case has a finite gap in some regions.The Heisenberg model can be solved exactly by the coordinate Bethe ansatz[1]or the quantum inverse scattering method.[2]Nowadays,Bethe ansatz becomes a popular method to calculate exact solutions of one-dimensional quantum many-body systems. The Heisenberg model is also a suitable candidate to check the validity of new numerical simulation technique and new physical pictures such as the spinon and fractional statistics.[3]

When the NNN interaction is involved, the most famous model is theJ1-J2model, which cannot be solved exactly. At the Majumdar-Ghosh point, i.e.,J2/J1=0.5, the Hamiltonian degenerates into a projector operator and only the ground state can be obtained exactly.[4]TheJ1-J2model withJ2/J1=0.241 possesses a Kosterlitz-Thouless-like quantum phase transition, which is a kind of topological phase transitions and does not have the local order parameter. The corresponding critical point has been studied by many methods such as the density matrix renormalization group[5]and fieldtheoretical approach.[6-8]Due to the competition between NN and NNN interactions, especially when the NN interaction is ferromagnetic and NNN interaction is antiferromagnetic,some interesting ordered magnetic states are found. TheJ1-J2model can be explained as the zigzag spin ladder, which is very important in the study of crossover from the onedimensional to the two-dimensional case. Therefore, much attention has been paid to the quantum spin chain with competing interactions.[9-12]

The DM interaction is a typical antisymmetric spinspin interaction, which plays an essential role in various fields.[13-15]For example, the DM interaction in the Heisenberg model can induce the spin glasses phase,[16]phase transition[17]and nonlinear excitations.[18]In recent years,DM interactions in magnetic systems have been studied extensively.[19,20]

The chiral three-spin couplings are another kind of interesting interactions.The chirality terms are used to characterize the chiral spin liquid state in the system.[21]It is proposed that the expectation value of the spin chirality operator can be used as the order parameter for chiral spin liquids.[22,23]Using the quantum transfer matrix method,researchers have studied the thermodynamic properties of this kind of models.[24,25]Recently,the models with chirality terms have attracted renewed interest in the theory of quantum spin liquids.[26,27]

The magnetic impurity in the strongly correlated systems is the eternal topic in the quantum magnetism theory.Many interesting mechanisms such as the Kondo screen,spiral phase,novel spinon excitation,ghost spin and boundary bound states are induced by the magnetic impurity. The Kondo problems in one dimension are solved by means of Bethe ansatz.[28,29]Using the language of integrable theory,some impurity problems are equivalent to the boundary magnetic fields. Here,we note that if the boundary magnetic fields are parallel,then theU(1)symmetry will be held and the system can be solved by the Bethe ansatz.[30]If the boundary magnetic fields are unparallel,then theU(1)symmetry will be broken and the conventional Bethe ansatz will not work. In this case,the system can be solved by the off-diagonal Bethe ansatz.[31]

In this paper,we put all the above-mentioned interactions(NN,NNN,DM,chiral three-spin couplings and boundary impurities) together and construct a new integrable model. The Hamiltonian is given by Eq. (1). For the most possible applications, we consider the case that the boundary fields are unparallel.Due to the off-diagonal boundary reflection,the total number of quasiparticles with fixed spin-component is not conserved. By means of the off-diagonal Bethe ansatz,we obtain the exact solution of the system.These exact solutions can be used to study some physical quantities such as the ground state,elementary excitations,and boundary energy.

The paper is organized as follows. The model Hamiltonian is explained in Section 2 and the integrability of the system is proved in Section 3. The exact energy spectrum and the Bethe ansatz equations are derived in Section 4. The exact ground state energies in some parameter regions are given in Section 5. Section 6 is attributed to the concluding remarks.

2. Model Hamiltonian

The integrable Hamiltonian considered in this study is

Let us explain Hamiltonian (1) more clearly. The interactions in the bulk are isotropic and the coupling strengths are chosen as

The integrability requires that the parametersJ1,J2andJ3are not independent. From Eq.(2),we also see that due to the existence of boundary magnetic fields, the couplings ofσ1·σ2andσ2N−1·σ2Ncan be enhanced or decreased by the boundary fields. The resulted coupling strengths could be different from that of other bonds in the bulk. The NNN interacting strengthJ2is a constant. Meanwhile,the signs of chiral three-spin interactions change with the changing site numberj. Thus the chirality terms are staggered.

3. Integrability

Now, we prove the integrability of Hamiltonian (1). We adopt the standard notations.Throughout this paper,Vdenotes a two-dimensional linear space. For any matrixA ∈End(V),Ajis an embedded operator in the tensor spaceV ⊗V ⊗···,which acts asAon thej-th space and as identity on the other factor spaces. ForB ∈End(V ⊗V),Bi jis an embedding operator ofBin the tensor space, which acts as identity on the factor spaces except for thei-th andj-th ones.

The integrability of Hamiltonian (1) is related with theR-matrix and the reflection matricesK±(u). TheR-matrix is

wherepis the boundary parameter which characterizes the strength of boundary field. The matrixK−(u)satisfies the reflection equation This implies that the transfer matrixt(u) is the generating function of all the conserved quantities. Hamiltonian (1) is constructed from the transfer matrixt(u)as

4. Exact solution

From the construction of Hamiltonian(1),we can see that the dual reflection matrixK+(u)has the off-diagonal elements.Thus theU(1)symmetry of the system is broken. We use the off-diagonal Bethe ansatz(ODBA)to solve Hamiltonian(1).

The main idea of the ODBA is as follows. From the definition of transfer matrixt(u),we know thatt(u)is an operator polynomial ofuwith the order of 4N+2. Denote the eigenvalue of the transfer matrixt(u)asΛ(u).Then we arrive at the case that the eigenvalueΛ(u)must be a polynomial ofuwith the order of 4N+2. Our task is to determine the polynomialΛ(u),which can be achieved by its values at arbitrary 4N+3 points (at least) or the 4N+3 constraints satisfied byΛ(u)in principle. From the crossing-unitary relation (15) of the transfer matrixt(u), we also knowΛ(u)=Λ(−u −1). Thus the number of constraints is reduced from 4N+3 to 2N+2.If these constraints are obtained, the eigenvalueΛ(u) can be completely determined.

Now,we seek these constraints.The matrixR(u)given by Eq.(3)degenerates into the permutation operator at the point ofu=θj. Using the properties of permutation operator,after tedious calculations,we obtain

Acting the operators product identities (19) on the eigenstate of transfer matrixt(u),we obtain the 2Nfunction relations

and{λj|j=1,...,2N}are 2NBethe roots. BecauseΛ(u)is a polynomial,the residues on right-hand side of Eq.(25)should be zero,which gives the constraints of Bethe roots:

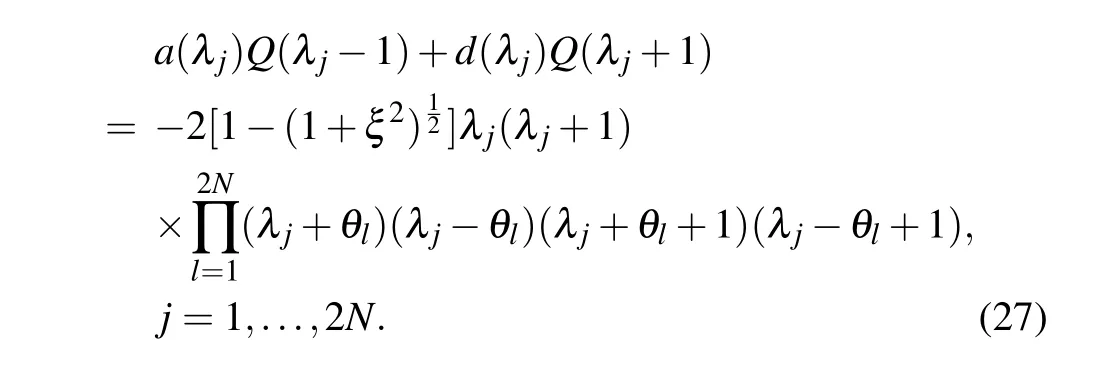
Solving the Bethe ansatz equations(27),we obtain the values of Bethe roots{λj|j=1,...,2N}. Substituting these values into Eq. (25), we obtain the eigenvalueΛ(u) of the transfer matrixt(u).

Now,we are ready to determine the eigenvalue of Hamiltonian (1). Substituting{θ2k−1=a,θ2k=−a|k=1,...,N}into Eq.(25),we obtain

We check the above results numerically for some small site numbers. We first solve the Bethe ansatz equations (30)with randomly chosen model parameters and obtain the values of Bethe roots. Substituting the values of Bethe roots into Eq. (31), we obtain the eigenvalues of Hamiltonian (1). The results are listed in Table 1. Next, we numerically diagonalize Hamiltonian(1)with same model parameters. We find that the eigenvalues obtained by solving the Bethe ansatz equations are exactly the same as those obtained by the exact diagonalization. Meanwhile, the expression (31) gives the complete spectrum of the system.

Table 1. Numerical solutions of the Bethe ansatz equations(30)with 2N=4,a=0.7i, p=−0.6,q=−0.3 and ξ =1.2. Here n indicates the number of energy levels and En is the corresponding energy. The energy En obtained from the Bethe ansatz equations is exactly the same as that calculated from the exact diagonalization of Hamiltonian(1).

5. Ground state energy

Now,we study the ground state energy of the system(1).Following the scheme suggested in Refs.[32,33],we find that the contribution of the third term in the inhomogeneousTQrelation (28) supplies theo(1/(2N)) correction which can be neglected in the thermodynamic limit 2N →∞. Thus, we introduce the following homogeneousT-Qrelation:

For the finite system size,Ehis the approximation solution of the system. With the increasing system size, the accuracy becomes higher. In the thermodynamic limit,Ehis infinitely tends to the actual value.

Next, we compute the values ofEh. For simplicity, we consider the case that ¯p ≥0 and ¯q ≥0. In the ground state,all the Bethe roots should take real values. Taking the logarithm of Eq.(35),we arrive at

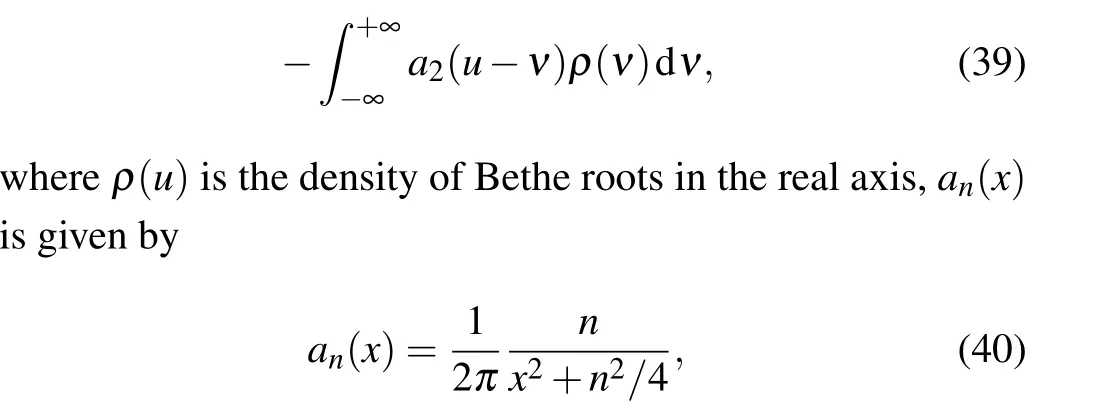
andδ(u±uh)are the boundary holes with the positions±uh.In the thermodynamic limit,the positions of holes would tend to infinity, and the holes contribute nothing to the energy.These boundary holes correspond to the Majorana modes at the two boundaries.[34]

We solve Eq.(39)using the Fourier transformation

According to Eqs. (36) and (45), we obtain the ground state energy of the system as follows:

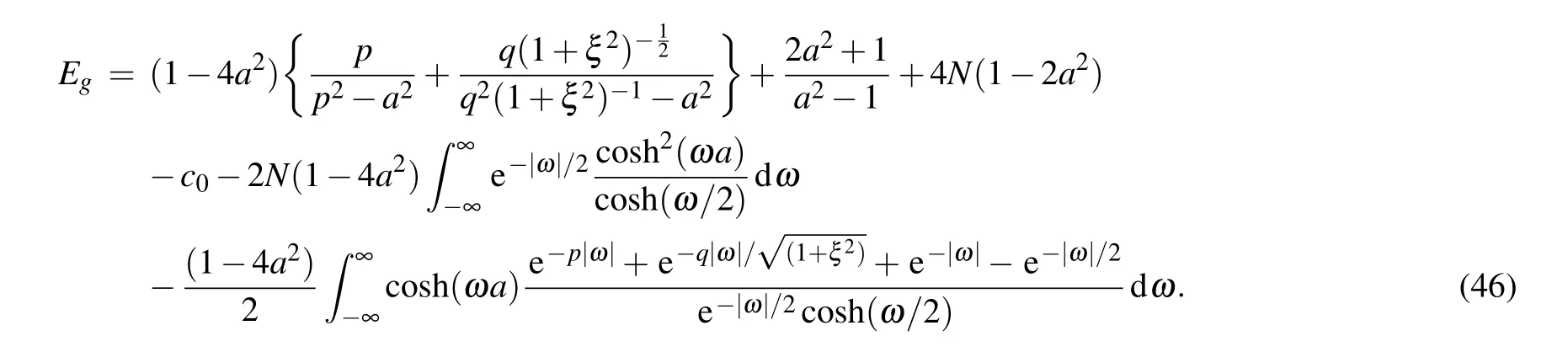
In order to show the correctness of Eq.(46),we calculate the ground state energy of the system(1)using the density matrix renomalization group(DMRG)method and compare the results with those obtained from Eq.(46),as shown in Fig.1. We can see that the energy difference ∆Etends to zero with the increasing system size. The data satisfy the scaling law ∆E=γ(2N)m,

wherem<0. Thus in the thermodynamic limit,the expression(46)gives the actual value of the ground state energy.

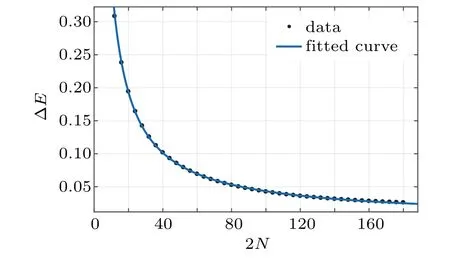
Fig. 1. The energy difference ∆E =ED −Eg with the different system sizes,where ED is the ground state energy calculated by using the DMRG method and Eg is the ground state energy calculated by Eq.(46).The model parameters are taken as a=0.66i, p=1.6, q=1.3 and ξ =1.2. The ∆E decreases with the increasing system size 2N and the data can be fitted as ∆E =3.124(2N)−0.9292. When the system size tends to infinity,the energy difference ∆E would be zero.

6. Conclusion

In summary, we have proposed a new integrable quantum spin chain which includes the NN,NNN,chiral three-spin couplings,DM interactions and unparallel boundary magnetic fields. By means of the off-diagonal Bethe ansatz, we obtain the exact solution of the system. The inhomogeneousT-Qrelation and Bethe ansatz equations are given explicitly. We further calculate the ground state energy in the regime of ¯p ≥0 and ¯q ≥0.

The method given in this paper can be used to construct other new integrable models with some interesting interactions. For example, if we start from the trigonometric or ellipticR-matrix,[2]we can study the anisotropic version of the integrable Hamiltonian(1). Meanwhile,if we put the alternate inhomogeneous parameters into theR-matrix[35]of the Hubbard model, we can construct an exactly solved strongly correlated electronic model which contains many possible physical processes. For example, besides the electrons hopping and on-site interaction, other terms such as the electron-pairs hopping, extended nearest-neighbor interactionsnjnj+1, and spin flipped behavior after reflecting. Due to the competitions among these couplings, some nontrivial phenomena such as the finite critical on-site interactionUcof the metal-insulator transition, new quantum states, novel charge and spin excitations may appear.

Acknowledgment

We would like to thank Professor Y. Wang for his valuable discussion and continuous encouragement.