Nearly invariant boundary entanglement in optomechanical systems*

Shi-Wei Cui(崔世威) Zhi-Jiao Deng(邓志姣) Chun-Wang Wu(吴春旺) and Qing-Xia Meng(孟庆霞)

1Department of Physics,College of Liberal Arts and Sciences,National University of Defense Technology,Changsha 410073,China

2Interdisciplinary Center for Quantum Information,National University of Defense Technology,Changsha 410073,China

3Northwest Institute of Nuclear Technology,Xi’an 710024,China

Keywords: boundary entanglement,optomechanical system

1. Introduction

Optomechanics,[1,2]which deals with nonlinear interaction between photons and phonons,has attracted a lot of attentions due to its potential applications in fundamental studies of quantum mechanics,precise measurement and quantum information processing.The single-photon optomechanical coupling is experimentally quite weak,[3,4]so a cavity with driving laser is needed to amplify the interaction effects.[5]With appropriate driving laser detuning, both cooling and heating of mechanical motions are reachable.[6]To raise the heating rate by increasing the driving power, the system goes to instability once the overall mechanical damping rate becomes negative.[7]

The transition from stability to instability might accompanying interesting quantum features in the vicinity of their boundary, for example, driving the system near the instability boundary can enhance the nonlinearity at single-photon level,[8]or increase the steady-state entanglement,[9]or exhibit divergent as well as negative susceptibilities, which is beneficial to quantum sensing.[10]Based on a three-mode optomechanical system, we even recently discover that the steady-state entanglement along the boundary line remains unchanged, and it is very robust to thermal phonon noise, thus providing a strong quantum signature of transitions from stable fixed points to limit cycles.[11,12]However,due to the calculation complexity, we can only resort to numerical integrations and the parameter space involved is very limited. Therefore,several questions arise: Does this phenomenon of invariant boundary entanglement depend on the specific model?Can we learn more from simpler models?

In this article,we will investigate the boundary entanglement in the simplest two-mode optomechanical system,where one optical mode is coupled with mechanical vibration by radiation pressure force.[13]With the help of some analytical calculation and discussing in a much bigger parameter interval, we find that the invariant boundary entanglement is by no means completely invariant, but the change is so small that it can be regarded as unchanged,and this nearly invariant boundary entanglement is a general phenomenon via parametric down conversion process in the weakly dissipative region,i.e.,the vibration has a very high mechanical quality factorQ,larger than the order ofO(103). This happens to be the region discussed in our previous three-mode system.[11,12]Most state-of-the-art experiments can reach the resolved sideband regime and the quality factor can range from 104to 109.[1]The nonlinear phenomena can be enhanced in this region with smaller mechanical damping rateγm=ωm/Q, since it needs less driving power to get instability. Besides, the nonlinear dynamics with red laser detuning also show sensitivity to initial conditions.[14]Here, we focus on the blue laser detuning to generate photon-phonon entanglement through typical parametric down conversion ∝e−iωLtˆa†ˆb†,whereωLis the pumping laser frequency, ˆa†and ˆb†are creation operators of optical and mechanical modes with frequenciesωaandωm, respectively. The value of boundary entanglement remains almost unchanged in a wide driving detuning interval around the resonant drivingωL=ωa+ωm,and equals approximately twice the ratio of intrinsical mechanical and optical damping rates when this ratio is much smaller than one.Since both the mechanism to generate entanglement and the parameter dependence of boundary entanglement are quite similar as in our threemode system, we believe that the two-mode system has captured the main features in the three-mode system. The studies in this paper can not only complement our former study on boundary entanglement,[11,12]but also extend to a more general conclusion that parametric down conversion plus weak mechanical dissipation can lead to nearly invariant boundary entanglement.

Our paper is organized as follows: in Section 2, we will review the two-mode optomechanical system and show our finding of nearly invariant boundary entanglement in this system. In Section 3, with some analytical calculation, we analyze how the boundary entanglement at resonant driving depends on the system parameters,and then compare the boundary entanglement in the weak and strong dissipation regions.In Section 4, we study and discuss how the boundary entanglement changes with various other parameters in the weak dissipation regime. In all these sections, we will mention the three-mode situations in appropriate places for comparison.In Section 5,we summarize our results.

2. Physical system and boundary entanglement

The two-mode optomechanical system, which contains the main characteristics of photon-phonon interaction, has been well studied in many aspects.[1]A typical experimental setup is a driven Fabry-Perot cavity with one mirror fixed and the other free to vibrate.[5]The Hamiltonian of the whole system is[13,15]

whenωm≫γm,[18]where ¯n=[exp(¯hωm/(kBT))−1]−1is the mean thermal phonon number at temperatureT.

In the case of weak couplingg0≪κand moderate drivingΛ, equation (2) can be solved by the mean-field approximation,[1]i.e., decomposing each operator ˆOinto its mean value〈ˆO〉≡Oplus the quantum fluctuationδˆOaround the mean value. By doing this,the equations of motion can be separated into two sets, one describes the classical behavior reflected by mean values,the other provides the quantum fluctuations around the classical orbit. The set of classical mean value equations takes the following form:

whose nonlinear classical dynamics has been widely studied including bistability,[19]limit cycles,[20]chaos,[21]etc. Its fixed points are the solutions by letting all the first-order derivatives to be zeros,i.e.,

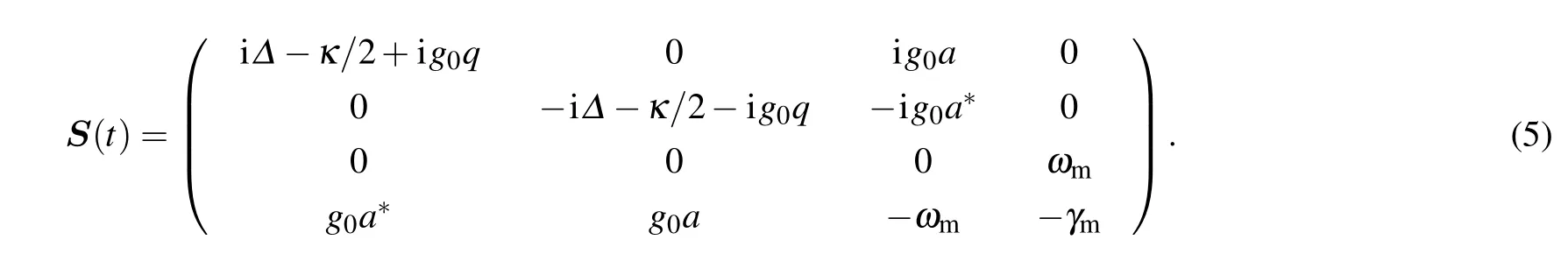
and the Jacobian matrixSis given by The dynamics ofS(t) is determined by Eq. (3), which combined with Eq. (4) can predict the quantum dynamics of the whole system as long as none of the Lyapunov exponents of the classical equations are positive.[22]To judge the stability of one particular fixed point, we evaluate matrixSat that fixed point. It is stable when all of the eigenvalues ofShave negative real parts.

To discuss the boundary entanglement in the two-mode system,we first plot the stability diagram as a function of the driving amplitude and driving detuning in Fig.1(a). The blue detuning(∆>0)region is chosen,where the resonant driving∆=ωmis included and each set of parameters has only one fixed point solution. The boundary line can be solved analytically from the eigenvalues ofSmatrix,but the expression is too cumbersome to be presented here.The black boundary line obtained from the analytical expression is completely consistent with the numerical results. It has a single peak pointing to the left at the resonant driving, where the interaction is most efficient thus the instability occurs at the lowest driving power.

Fig. 1. (a) Two-dimensional stability diagram of the system with respect to the driving amplitude Λ/κ and driving detuning ∆/κ,where parameters used are g0/κ=0.02,ωm/κ=20,and γm/κ=0.01.The yellow part on the left is the stable area,and the blue part on the right is the unstable area. This color division is the result of numerical calculation,while the black boundary curve is given by a lengthy analytical expression. (b)The corresponding boundary entanglement EN,b of panel (a) as a function of driving detuning∆/κ with ¯n=0.

Figure 1(b) shows the boundary entanglementEN,bof Fig.1(a)as a function of driving detuning. The entanglement rapidly increases from zero to a saturation value≃0.0198.In the case of resonant driving with∆/κ=ωm/κ=20, the efficiency of generating entanglement is the highest and the threshold of instability is the lowest. While in the case of driving away from resonance, the instability threshold increases despite the decrease in efficiency. These two factors compensate each other to keep the boundary entanglement increasing more and more slowly as the detuning increases, almost looking like a horizontal line. The entanglement values are all very close to the saturation value 0.0198 for∆/κ ∈[15,28].This segment can be regarded as having a invariant boundary entanglement value. It cannot be invariant in the entire range, because different segment ranges may correspond to different interactions. When∆/κis close to zero, the effective Hamiltonian has another half contribution from the beam splitter interaction ∝g0(aδˆa†δˆb+a*δˆaδˆb†), and the entanglement is zero. By increasing the driving detuning,the twomode squeezing term becomes more important and the entanglement increases quickly to a saturation value. This slower and slower increasing behavior of boundary entanglement is also true for∆/κgoes beyond 28. But when∆/κis large to a certain extent,the contribution of both two-mode squeezing and beam-splitter interactions are negligible due to large detuning,the whole system is always stable. Thus the boundary line will first increase and then drop down as the driving amplitude increases. The smaller the mechanical frequency,the smaller the value of∆/κat the turning point where the boundary line rises and then falls. We are only interested in the vicinity of the resonant driving where the parametric down conversion is most prominent,so the maximum∆/κis set to be 28. In our former work,[11,12]the phenomenon of invariant boundary entanglement has been discovered around the resonant driving, here we give its overall change based on a simpler system,and further find that the boundary entanglement is actually nearly invariant in a larger driving detuning interval.

3. Weak versus strong dissipation

In this section,we will first try to figure out how this saturation value of boundary entanglement depends on system parameters. Since this value is also the boundary entanglement at resonant driving∆/κ=ωm/κ,this special boundary point can be focused for analysis. Here, we take advantage of analytical calculation,which cannot be possible in the three-mode system.In the case ofωm≫γmand after the rotating wave approximation with∆=ωm, the linearized quantum Langevin equation can be equivalently written as follows:[1]

The boundary entanglement at resonant drivingEN,b,resas a function ofγm/κis plotted in Fig. 2. It increases linearly whenγm/κis very small,i.e.,EN,b,res≃2γm/κ, further increases with the increase ofγm/κto reach a maximum atγm/κ=1, then decrease monotonously whenγm/κ> 1. The numerical integration adopted in Section 2 and the analytical result in Eq.(10) agree very well almost in the whole range, only deviating a little bit whenγm/ωmis larger than 0.1. Whenγmis very small, the boundary threshold powerΛ2th,resis also weak, resulting in small entanglement.Increasingγmcan raise the threshold powerΛ2th,res, thus enlarge the effective coupling strengthg0as. However,the largerγm, the more impact from the environmental noise. There is a trade-off between these two factors. From the symmetry, the entanglementEN,b,resonly depends on ratio of two damping rates and none of the two modes is more special.ConsequentlyEN,b,res(γm/κ) =EN,b,res(κ/γm) and the maximum is achieved whenγm/κ=κ/γm= 1. There is one by one correspondence for all the other ratios, for exampleEN,b,res(0.5)=EN,b,res(2)≃0.588.

Fig.2. Variation of boundary entanglement at resonant driving EN,b,res (i.e.,boundary entanglement at ∆/κ = ωm/κ) with mechanical damping rate γm/κ,where solid black line is plotted by Eq.(10),and the red dotted line is obtained from numerical calculation with the same parameters as in Fig. 1 except that γm/κ is now a variable. The curve satisfies a linear relationship EN,b,res ≃2γm/κ when γm/κ is very small.

Fig. 3. (a) Stability boundary curves with different mechanical damping rates γm/κ, while keeping all the other parameters as in Fig. 1. The corresponding boundary entanglement curves are divided into two groups of weak and strong dissipation, respectively, placed in panels (b) and (c) for comparisons.

4. Discussion on weakly dissipative region

In the following,we will elaborate on how other parameters affect the boundary entanglement in the weak dissipation regime. Theγm/κ=0.01 is fixed as that in Fig. 1 for comparisons,so the remaining parameters areg0/κ,ωm/κ,and ¯n.While discussing one of the them,the other parameters are the same as in Fig.1.

Fig.4.Stability boundary curves and corresponding boundary entanglement with different choices of g0/κ are given in panels (a) and (b) respectively,while keeping all the other parameters as those in Fig.1.

In Fig.5(a),the resonant driving peaks of boundary lines shift up or down with the mechanical frequencyωm/κ, and the lowest driving thresholdΛth,res/κ,which is proportional toωm/κ, cause the curves to move left and right. The shape of boundary lines below the resonant driving also becomes less concave with smallerωm/κ. Figure 5(b) demonstrates the boundary entanglement with different values ofωm/κ. The entanglement curves have very similar behavior, rising from zero and approaching the same saturation value quickly,which can be approximately viewed as translation of curves. This is consistent with the result that the saturation value is only determined byγm/κ.As mentioned above,the condition to observe invariant boundary entanglement in the three-mode system is 2J=ωm. Changingωm/κalone means deviating from that resonant condition, the boundary entanglement curves will drop down with increasing driving detuning.[12]However, ifωm/κandJ/κchange at the same time to maintain the resonant condition, different curves will overlap in the form of horizontal straight lines.

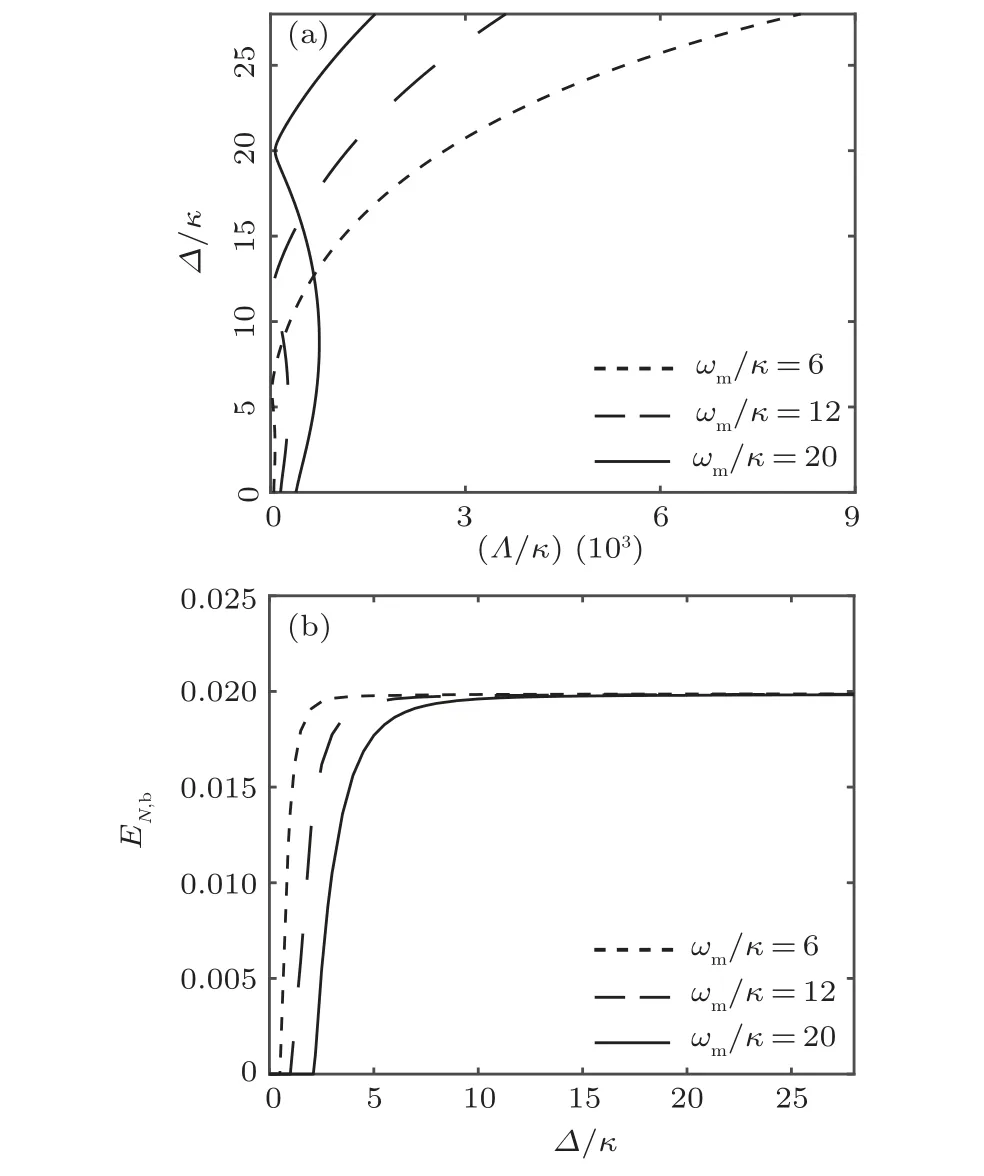
Fig.5.Stability boundary curves and corresponding boundary entanglement with different choices of ωm/κ are given in panels(a)and(b)respectively,while keeping all the other parameters as those in Fig.1.

Finally,the influence from temperature is considered,embodied by the mean thermal phonon number ¯n. Figure 6(a)shows how the boundary entanglement at resonant driving in Fig. 1(b) varies with ¯n. It decreases approximately linearly with the increase of ¯n,i.e.,EN,b,res≃max[0.0198−0.0002¯n,0]. At ¯n=100, the entanglement drops to zero. We expect that the boundary entanglement curve behave similarly as in Fig. 1(b) with only the saturation value decreased with larger ¯n. However, smaller driving detuning is more sensitive to ¯nas shown in Fig. 6(b), thus in contrast to the almost horizontal line with ¯n=0, the curves have a more obvious upward trend as ¯nincreases, reducing the effect of obtaining nearly invariant boundary entanglement in a wide detuning interval. For ¯n=10 and∆/κ ∈[16,24], the difference between the maximum and minimum is about 5%. If you narrow this segment, the difference will be smaller. This is why invariant boundary entanglement can be observed with¯n=50 in our former work.[11]The temperature influence on the boundary entanglement curves has not be discussed in the three-mode case.[12]Figure 6(c)shows the steady-state entanglementEN,resalong the resonant driving∆/κ=20 with different ¯n. The entanglement near the instability boundary is robust to thermal phonon noise, while the entanglement far away from the boundary drops down quickly with a non-zero¯n. With ¯n=0, the entanglement changes very slowly when approaching the boundary,which facilitates the experiment to observe the value of boundary entanglement if the fluctuations of driving field intensity is considered.

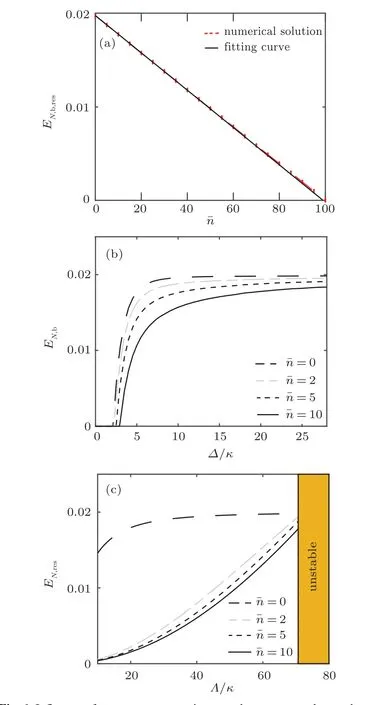
Fig.6. Influence of temperature on various steady-state entanglement based on the stability diagram in Fig. 1: (a) boundary entanglement at resonant driving EN,b,res (i.e.,∆/κ =20),where the expression for linear fitting line is given in the main text;(b)the boundary entanglement curve EN,b;(c)the entanglement at resonant driving EN,res,which shows how the entanglement changes when approaching the boundary from the stable region.

5. Conclusion

To summarize, we have studied in detail the boundary entanglement in the simplest two-mode optomechanical system. Through this simpler system, we fully understand the phenomenon of invariant boundary entanglement numerically discovered in our former work.[11,12]The word “invariant”here is by no means completely invariant, but the change in a large parameter range is so small such that we regard it as unchanged. To be more precise, “nearly invariant” boundary entanglement could be better. Besides, all the same parameter dependencies in the weakly dissipative region as that in previous three-mode optomechanical system are obtained,i.e., the value for boundary entanglement is proportional to the ratio of mechanical and optical damping rates,and it does not change with the optomechanical coupling strength or the mechanical frequency.[12]The similarities of both the mechanism in generating the entanglement and the parameter dependence of boundary entanglement fully illustrate that the two-mode system has captured the main characteristics of the three-mode system. Furthermore, we give an overall picture of how the boundary entanglement changes in a much bigger driving detuning interval,assisted by some analytical calculation and combined with the common results of both models to find out that the nearly invariant boundary entanglement is a general phenomenon produced by parametric down conversion in the weakly dissipative region. The temperature will influence the effect of keeping invariant in a wide driving detuning interval. However, with very high mechanical frequency and low temperature, mean thermal phonon number smaller than 1 should be possible. With thermal phonon number almost zero, the value of boundary entanglement could still be observed in spite of fluctuations of driving field intensity. The main challenge is that the invariant boundary entanglement is weak, which might be difficult to measure in realistic system. For example, withγm/κ ≃1.6×10−5in Ref. [30], the value for boundary entanglement is only 3.2×10−5. Anyway,the nearly invariant boundary entanglement is definitely interesting as threshold quantum signatures in optomechanical phonon lasers,or might have potential applications where the quantum properties of the boundary is utilized.

Acknowledgment

One of the authors(Zhi-Jiao Deng)is grateful to Jie-Qiao Liao for useful discussions.