基于固端弯矩相等原则的等效荷载法

黄 欢， 唐贵和， 李文雄*， 叶云青

(1.华南农业大学水利与土木工程学院， 广州 510642； 2.广州瀚华建筑设计有限公司， 广州 510655)

结构力学中的计算方法众多，龙驭球[1]在《结构力学方法论的哲思回望》中站在哲学的角度对结构力学中的各种主流方法进行了深刻的剖析，其中位移法被认为是结构力学中重要方法之一。在线弹性范围内，一定的外因作用下，结构的内力与变形之间具有固定的关系，也可以认为确定的内力总是和确定的位移相对应[2]，它便是建立位移法的基础。位移法通过建立单跨超静定梁的杆端力与杆端位移之间的关系，实现超静定结构的求解。在位移法的基础上，为了避免求解联立方程组，进一步发展了力矩分配法，为工程试算提供了便捷的计算手段。在当下计算机技术发达的情况下，依然不乏从结构力学概念出发去解决实际工程问题的案例[3-5]。

实际上，无论是位移法还是力矩分配法，几乎都绕不开对固端弯矩的计算。俞瑞荣[6]以力法为基础，通过简支梁弯矩图的面积及其形心推求了等截面单跨梁固端弯矩的一般公式。孙晔青[7]采用力法研究了一端固定、一端定向支承的斜梁的转角位移方程和两端固端弯矩。樊友景等[8]在研究有侧移斜杆时基于荷载等效变换的思想研究了斜杆在简单的常规荷载下的固端弯矩。罗双等[9]利用虚功原理推导并建立了混凝土结构正负受弯区刚度不同情况下的单跨连续梁的固端弯矩和转动刚度系数。固端弯矩可为后续的力学分析提供便利。

在力学分析中，为了避免求解方程组，力矩分配法作为在位移法基础上发展起来的一种渐进算法，得益于其概念清晰，易于掌握，且适合手算。它的计算过程分为两步，首先是确定各单跨超静定梁的固端弯矩，然后是通过力矩分配和传递实现内力调整，最终得到结构的内力结果。对于常见的跨内集中荷载或均布荷载的情况，可直接利用位移法中的载常数表确定其固端弯矩[10]。然而，对于无法直接利用载常数表确定其固端弯矩的复杂荷载情况，通常需要借助线性叠加法的方法，将多荷载作用下梁的固端弯矩表示为多个单荷载作用下的固端弯矩叠加的形式。此外，对于一些三角形分布荷载，在位移法的载常数表中虽有罗列与归纳，但不易被人们记忆，导致其在力矩分配法使用上的不便。

在实际工程问题中，对称集中荷载和三角形分布荷载是常见的形式。若能通过等效荷载代替这些常见的荷载形式，直接获得其固端弯矩，便能建立一种比线性叠加法具有更高效率和实用性的计算方法。本文基于固端弯矩相等原则，即利用单跨超静定梁在等效荷载和原荷载作用下固端弯矩保持一致的条件，推导在对称集中荷载、三角形分布荷载和任意荷载作用下的等效荷载施加方法，进而结合载常数表直接算得单跨超静定梁的固端弯矩，为力矩分配法及其他的力学分析提供一个便捷的思路。最后通过连续多跨梁和框架结构验证了所提方法的可行性。

1 静定结构中的荷载等效变换

在静定结构受力问题中，荷载等效变换是指采用将一种原荷载变换为另一种等效的荷载[2, 11-12]。荷载等效变换应满足以下两点：一是原荷载与等效荷载的主矢应相同；二是原荷载与等效荷载对同一点之矩应相等。图1(a)为对称集中荷载F作用下长度为l的简支梁，其中左侧荷载F作用点C与左侧支座A的距离为a，右侧荷载F作用点D与右侧支座B的距离为a。图1(b)中的荷载即为图1(a)中对称荷载的静力等效荷载，并分别绘制出梁在原荷载和静力等效荷载作用下的弯矩图。

从图1可知，除CD段之外，梁在原对称荷载和等效荷载作用下的弯矩图是完全一致的。这实际上是静定结构的重要特性，即当作用在静定结构的某一几何不变部分的荷载在该部分范围作等效变换时，只有该区域的内力发生变化，而其余区域的内力保持不变[2，12]。

图1 简支梁受对称荷载及等效荷载情况下的弯矩Fig.1 The bending moment diagrams of a simple supported beam subjected to the symmetrical loads and the equivalent load

2 单跨超静定梁的荷载等效变换

超静定结构的等效荷载变换规律并不一定与静定结构相同，需根据具体问题进行分析。以对称集中荷载作用下的单跨超静定梁为研究对象，探讨等效荷载的施加方法。图2为受两个对称分布的集中荷载的等截面单跨梁，杆长为l，左边的集中荷载F与梁左支座的距离为a，与右支座的距离为b，右边的集中荷载F与之对称。

可根据线弹性体系的叠加原理确定梁的固端弯矩。首先，将该受力体系分解为两个只受单一集中荷载F的体系，如图2(b)和图2(c)所示。然后根据位移法中的载常数(表1)[10]算得图2(b)和图2(c)两种加载条件下梁的左右两端的固端弯端弯矩，最后通过叠加得到图2(a)中梁的固端弯矩和弯矩图，其中固端弯矩为

(1)

(2)

式中：MAB和MBA分别为单跨超静定梁A端和B端的固端弯矩。

上述即为利用叠加原理的求解过程。下面介绍本文提出的基于等效荷载的求解方法，即以梁在等效荷载和原荷载作用下固端弯矩保持一致的原则建立的等效荷载法。为简单起见，此处采用单一集中荷载Fe作为等效荷载(图3)，代替图2中的对称荷载F。

根据表1可计算出图3单跨超静定梁两端的固端弯矩，即

(3)

图2 单跨超静定梁受对称荷载作用Fig.2 A single-span indeterminate beam under symmetric loads

表1 单跨超静定梁的载常数

图3 单跨超静定梁受等效荷载作用受力图Fig.3 Force diagram of a single-span indeterminate beam under equivalent load

(4)

于是得

(5)

则等效荷载为

(6)

式(6)即为所求的等效荷载。最后根据表1得到固端力并绘制出图2(a)和图3荷载作用下的弯矩图，如图4所示。可以看出，单跨超静定梁在等效荷载作用下，只有端部截面的弯矩和原体系是等效的，其他截面的弯矩已经失真，主要原因在于等效荷载是基于固端弯矩相等的原则建立的。显然，直接基于等效荷载求对称荷载作用下单跨超静定梁的固端弯矩更为便捷。

图4 单跨超静定梁在原对称荷载和等效荷载作用的弯矩图Fig.4 The bending moment diagram of a single-span indeterminate beam under the original symmetrical loads and the equivalent load

接下来，考察上述单跨超静定梁的实际荷载和等效荷载之间的关系，可得

(7)

考虑到a+b=l，则有

0≤Fe≤2F

(8)

即等效荷载Fe应在闭区间[0, 2F]上取值。

将b=l-a代入式(6)并整理后可得

(9)

因为a∈[0,l/2]，所以Fe在此区间具有单调性。当对称荷载F分别作用在支座A和支座B时，Fe=0；当对称荷载F作用在跨中时，Fe=2F，且为Fe的最大值。显而易见，只有当对称荷载F作用在跨中时，等效荷载才会与原荷载具有相同的合力且对同一点产生相同的力矩。

综上可知，对于单跨超静定梁而言，基于梁端固端弯矩相等的原则进行荷载等效变换，通常只能保证在等效荷载作用下的固端弯矩是准确的，无法确保其他截面也得到准确的弯矩。但由于梁端弯矩已经确定，因此可进一步基于实际荷载(叠加上实际荷载作用下简支梁的弯矩图)方便地得到梁中弯矩的实际分布。基于固端弯矩等效的原则可得到单跨超静定梁在不规则荷载或对称荷载情况下的等效荷载，为快速获得梁端固端弯矩提供了一种可行的途径。表2为若干单跨超静定梁在对称集中荷载和三角形分布荷载作用下的等效荷载图及等效荷载值。

3 单跨超静定梁在任意集中荷载下的等效变换

重点介绍对称集中荷载作用下单跨超静定梁等效荷载的计算。由此可推而广至一般的荷载情况，如多个任意集中荷载作用于单跨梁的情况。下面对其进行相关研究，图5为受任意集中荷载作用的单跨超静定梁，根据叠加原理可得该梁的固端弯矩为

(10)

式(10)中：Fi为图5中第i个荷载；ai和bi分别为荷载Fi距离左端A点和右端B点的距离，i=1,2,…,n。

将bi=l-ai代入式(10)并整理得

(11)

同样地，也可得B端的固端弯矩为

(12)

梁的等效荷载如图6所示，设Fe为等效荷载的数值，ae和be分别为等效荷载作用点与A、B端的距离，等效荷载图中的梁端固端弯矩分别为

表2 非常规荷载作用下单跨超静定梁的等效荷载

(13)

(14)

取式(14)中两个方程的比值，可得

(15)

将ae和be代入式(14)中的第一个方程，可得等效荷载为

(16)

式(16)即为所求单跨超静定梁在任意集中荷载作用下的等效荷载。

推导式(14)～式(16)时仅考虑了两端固结的情况，对于一端固结一端铰支的情况，确定等效荷载更为容易，因为只需要满足一端固端弯矩即可，不再对此进行推导。针对任意的分布荷载，也可按照上述思路并利用积分确定等效荷载图。在实际工程问题中，作用在单跨梁上的集中荷载往往具有一定的规律，如对称、等值等特点，因此，式(16)还可以进一步进行简化，使其实用化。

图5 多个任意集中荷载作用下单跨静定梁受力图Fig.5 Force diagram of a single-span indeterminate beam under more arbitrary external loads

4 算例分析

算例1多跨连续梁如图7所示，该梁各段抗弯刚度EI为一常数，其中E、I分别为弹性模量和截面惯性矩，试用力矩分配法求该梁的弯矩图。

1、2、3、4和5为梁上的5个结点编号图7 多跨超静定梁受力图Fig.7 Force diagram of a multi-span indeterminate beam

(3)进行力矩分配与传递，如图8所示。

(4)绘制弯矩图：当杆端弯矩确定的前提下，考虑实际荷载的作用，采用叠加原理即可绘制最终的弯矩图(图9)。需要特别注意的是，由于12杆和45杆上作用的是三角形分布荷载，弯矩图在此区域以三次曲线变化，在绘制时需要找到简支梁单独在三角形分布荷载作用下的弯矩的驻点位置及弯矩值，这样绘制出的弯矩图更为准确。

(5)校核：为了检验结果的正确性，采用有限元软件Sap2000对本算例进行建模分析，计算结果如图10所示。可见，图9和图10的弯矩图吻合较好，验证了结果的正确性。

M为弯矩图8 弯矩的分配与传递Fig.8 Processes of moment distribution and carryover

图9 多跨超静定梁弯矩图Fig.9 Bending moment diagram of the multi-span indeterminate beam

图10 Sap2000的计算模型弯矩图Fig.10 Bending moment diagram of the multi-span indeterminate beam in Sap2000

算例2某两层一榀两跨的框架结构如图11所示，梁构件的截面尺寸均为0.5 m×0.25 m，柱构件的截面尺寸均为0.5 m×0.5 m，材料的弹性模量E=2.49×107kN/m2。

采用所提出的等效荷载法，将编号为⑤和⑨梁上的对称荷载转换为一个跨中的集中荷载8Fab/l2=15 kN(表2)，如图12所示。为叙述方便起见，将荷载转换前的受力情况称为工况1，将荷载等效转换后的情况称为工况2，分别采用Sap2000进行计算，并绘制出弯矩图，如图13所示。可以看出，除了编号⑤和⑨梁上跨中部分的弯矩不同外，其他各构件的弯矩并不受影响，因此在获得梁端弯矩的情况下再根据⑤和⑨号梁上的实际荷载绘制出其真实弯矩即可，其他内力可根据实际受力平衡确定。本算例再次验证了所提方法的正确性和可行性。

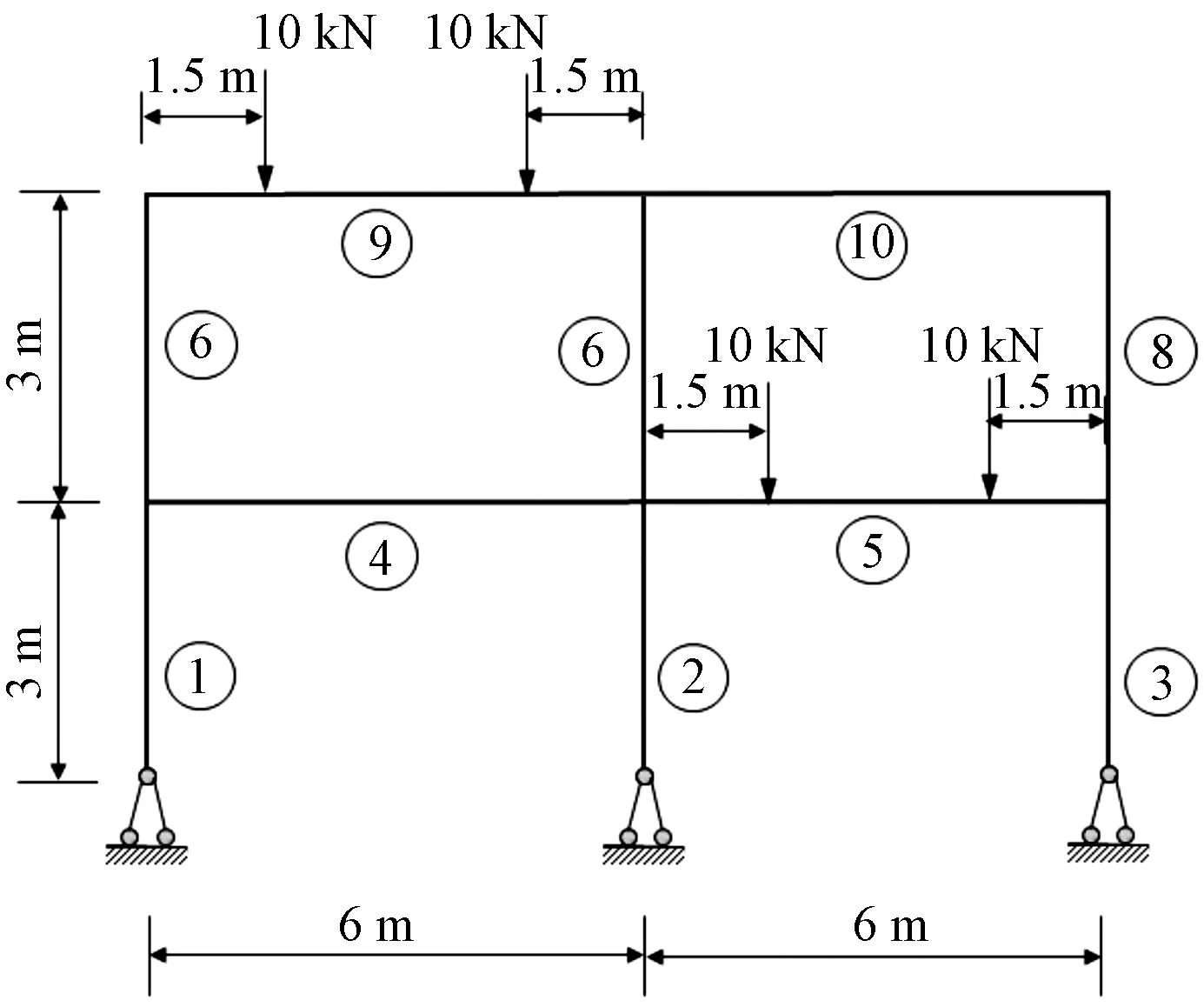
①～⑩为该框架中对应构件的编号，其中在编号为⑤和⑨的 梁上分别作用一对称荷载10 kN，忽略梁和柱的自重图11 框架结构受力图Fig.11 Force diagram of a frame structure

①～⑩为该框架中对应构件的编号图12 框架结构等效荷载图Fig.12 Equivalent force diagram of a frame structure

图13 工况2的框架弯矩图Fig.13 Bending moment diagram of the frame structure for case 2

5 结论

提出了超静定梁的等效荷载解法。以对称集中荷载和三角形分布荷载作用下的单跨超静定梁为例，推导了等效荷载变换公式及其特点。进一步探讨了任意多集中荷载作用下单跨超静定梁的等效荷载确定方法。采用等效荷载可直接获得固端弯矩，为其在力矩分配法及其他力学分析中的应用提供了便利，且不失为一种有效的解题方法。算例表明所提方法的可行性和便捷性。