不同加卸载条件煤岩裂隙面形貌分形各向异性特征研究
宋金旺,刘依婷,高明忠,谢 晶,郭万忠,付茂全,王 飞,刘贵康,叶思琪
(1.大同煤矿集团有限责任公司,山西大同 037001;2.四川大学水利水电学院,四川成都 610065)
煤炭在我国的能源中处于重要的地位[1],同时煤层气在全球性能源结构调整中的比重越来越大[2-3]。在煤炭及煤层气的开采中,煤层变为高裂隙度的裂隙岩体,裂隙体结构的存在对岩体的稳定性评价、渗流规律、破坏力学性质等有着重要的影响,而科学、精确地描述裂隙面粗糙形貌特征是研究裂隙岩体力学的基本前提。目前关于裂隙面或者裂隙的形貌特征的研究,国内外学者主要采用了凸起高度表征法、节理粗糙度系数JRC 表征法[4-10]和分形表征法。由于裂隙分布、裂隙面形貌起伏特征难用统一的指标对其复杂程度、粗糙程度进行定量描述,近年来基于分形理论的裂隙面形貌特征相关研究报道也逐渐进入研究视野,例如谢和平[11-13]采用分形统计的方法分析了岩石断裂表面分形测量中的尺寸效应,提出了可靠的分形测量的途径。对于研究粗糙尺寸较大的岩石, 分形维数描述方法不适用于与其力学性能建立联系,易成[14]、张亮[15]等提出了1 种新的描述表面粗糙形貌的分维指标Rd。张科[16]、WONG K T[17]、马尚权[18]等采用分形方法对破坏后的含孔多裂隙岩石新生裂纹进行研究,发现裂纹几何分布的分形维数D 与破坏特性密切相关。陆瑞全[19]、李佩禅[20]等利用多重分形理论,分析了剪切裂隙非均匀分布特征。许刚刚[21]、杨朋[22]、王志国[23]等对裂隙分形特征演化规律进行了研究。张来娣[24-25]等采用多重分形理论对页岩裂隙形貌特征进行研究。赵阳升[26]等在以岩体破坏裂隙面分布具有分形特征为前提条件,建立了关于岩体破坏裂隙面的三维分形仿真模型。李果[27]、刘京红[28]、赵小平[29]等人采用CT 图像重构技术对煤岩裂隙进行分形研究。于贺、李守巨[30]等根据分形几何理论,以岩体裂隙系统统计地质资料为基础,建立了用来描述岩体裂隙面网络几何特征的分形模型。可以看出,分形理论已经广泛应用于岩石裂隙体结构特征的定量描述研究中。岩体性质的尺寸效应是指利用相似条件对几何相似的同一性质岩体试件进行加载,得到的岩体特性随试件尺寸而变化的现象。岩石性质与尺寸无关的最小体积为代表性单元体REV(Representative Elementary Volume)[31-32]。在破坏行为下固体材料呈现出了尺寸效应,这一直是固体破坏理论中的1 个难以解决的问题。杨圣奇[32,33]等基于岩石的应变强度理论,建立了考虑尺寸效应的单轴压缩下岩石损伤本构模型,研究了岩样尺寸对岩石强度以及破裂形式的影响规律。吕兆兴[33]等开展了非均质数值试验,得出非均质参数对岩石材料强度的尺寸效应。李建林[34]等在岩体尺寸效应研究现状基础上, 研究了关于卸荷岩体的尺寸效应问题。国外对岩石尺寸效应与应变速率等方面的关系进行了大量试验,并取得了一些研究成果[35-37]。可以看出,国内外学者主要研究了岩石力学行为的尺寸效应,但对于裂隙面形貌特征的尺寸效应研究少有涉及。综上,目前岩石裂隙面形貌特征研究大多仍采用单一指标,结合典型破坏形式的裂隙面的分形各向异性特征及其尺寸效应的耦合分析涉及较少。因此,结合分形理论以及CATIA 三维模型重构处理平台,研究典型复杂破坏路径作用下煤岩裂隙面分形各向异性特征以及尺寸效应。
1 煤样裂隙面获取与重构
1.1 煤样和裂隙面
1)煤样制备。原则上选取煤块尺寸大于250 mm×250 mm×200 mm,且完整性较好、无明显裂隙的煤块进行加工。现场取出的煤样加工成长宽高均为100 mm 的立方体用于室内试验,煤样各表面不垂直度和不平行度小于0.02 mm。选取煤样基本信息见表1。
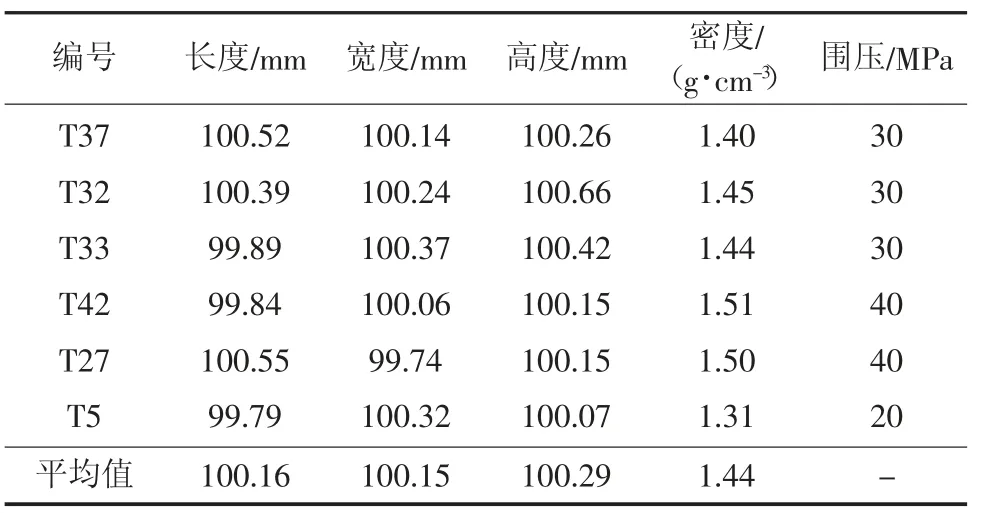
表1 煤样基本信息Table 1 Basic information of coal samples
2)裂隙面获取。为获取复杂破坏路径作用下形成的岩石裂隙面,将煤样加工为裂隙煤样,基于加卸载试验产生煤岩裂隙面。通过不同的加卸载方式,所得到的煤样破坏形式不同。选取不同应力路径下获取的、破坏面较为完整的煤样。不同工况下的煤样破坏特征统计见表2。
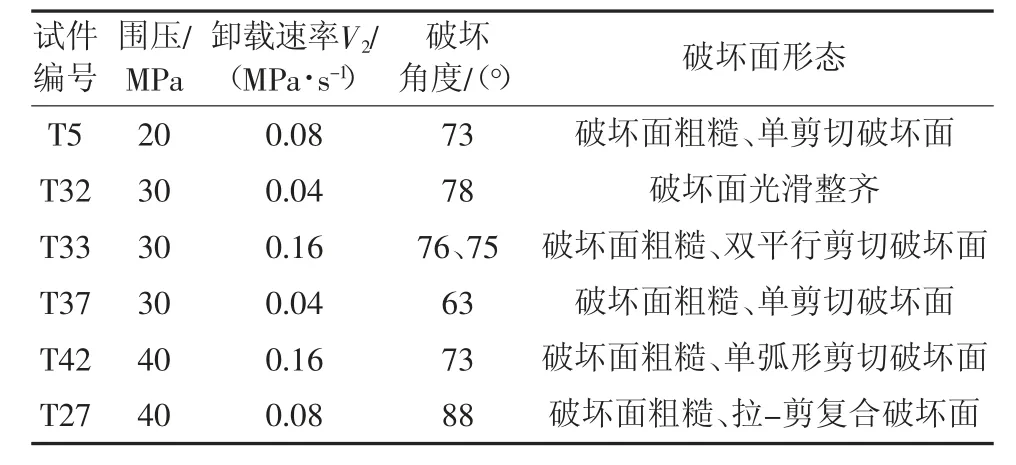
表2 煤岩体破坏特征统计表Table 2 Statistical table of failure characteristics of coal and rock mass
1.2 裂隙面的扫描与重构
为获取复杂应力路径下的岩样裂隙面形貌特征,采用型号为PRINCE775 的激光扫描仪,利用手持激光扫描仪三维数据采集系统对筛选的煤样进行扫描。扫描岩样裂隙面时利用ScanViewer 软件生成扫描数据,进行快速标定,设置扫描参数后,将岩样贴上标记点,选择标记点进行扫描,并将处于同一平面的标记点设为背景,选择激光点进行扫描。
通过扫描得到的破坏裂隙面形貌数据以ASC文件格式进行保存,利用手持激光扫描仪自带的软件Geomagic Studio 进行数据的预处理以及模型的重构,删除扫描过程中除裂隙面以外的一些杂点,建立坐标系,最终获得以扫描点水平方向坐标x、竖直方向坐标y 以及扫描点高度z 为坐标形式的数据。针对扫描复杂破坏路径下得到的破坏裂隙面所获得的形貌数据,初步对裂隙面进行空间起伏频谱分析,典型裂隙面空间起伏频谱分布特征如图1。煤样裂隙面扫描图如图2。
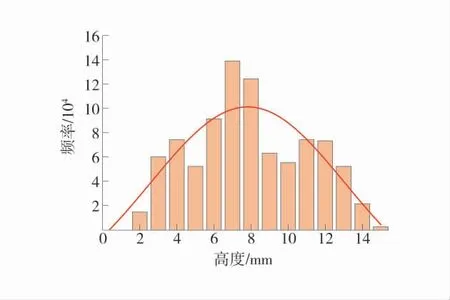
图1 典型裂隙面空间起伏频谱分布特征Fig.1 Spatial fluctuation spectrum distribution characteristics of typical fracture surfaces

图2 煤样裂隙面扫描图Fig.2 Fracture plane scanning of coal samples
由图1 可知,裂隙面的空间起伏分布情况基本符合正态分布。对于分布区间来说,复杂破坏裂隙面的高度起伏分布区间为1~15 mm,裂隙面形貌起伏明显。
由图2 可知,复杂应力路径破坏下的煤样裂隙面起伏高度较大,整个面并不完全处于1 个平面内,裂隙面并不平整,边界处也残缺不齐,这与煤岩自身性脆易碎以及黏结性不强的性质有关。同时由于加卸载试验较为复杂,导致了所得裂隙面破坏严重。
针对复杂破坏路径下的裂隙面,根据断裂力学知识,推测其宏观破坏背后的微细观力学机制,可以认为复杂破坏过程主要以沿晶断裂耦合穿晶断裂的形式为主,导致裂隙结构差异性明显,同时,由于煤样本身就存在初始裂纹,从而影响了整个裂纹扩展形成的粗糙裂隙面。
2 复杂应力路径破坏裂隙面分形各向异性特征
由于部分煤样裂隙面破损比较严重,对后期处理和分析的结果可能会有影响,因此后期选取了裂隙面相对较完整的各应力路径下的T32、T33、T37 3个煤样进行后面的处理和分析。
2.1 裂隙面分析原理
真实的裂隙面具有多维度的分形特征,根据扫描获得的裂隙面形貌数据点(x,y,z)相关信息,结合相应的分形维数计算方法进行计算。目前对一维粗糙曲线的分形维数的计算方法有码尺法、盒维数法(覆盖法)等、和一维曲线类似,二维粗糙面的分形维数计算方法包括投影覆盖法(PCM)[38]、三棱柱表面积法(TPSAM)[39]、立方体覆盖法(CCM)[40]以及改进的立方体覆盖法(ICCM)[41]。本研究对迹线分维采用盒维数法(覆盖法),对面分维的计算采用的是立方体覆盖法,利用Matlab 进行编程计算。
2.1.1 盒维数法
用正方形的格子(δ×δ)覆盖曲线,格子的大小是有变化的。给定盒子的码尺δ,覆盖曲线所需要的总格子数量记为N[42]。假设第i 步使用覆盖的格子为δi×δi,需要的盒子数目为Ni(δi),在第i+1 步需要的覆盖格子δi-1×δi+1,则盒子数目需要Ni+1(δi+1)。可以发现在不同2 个尺寸下所需要的盒子数之比与码尺之比存在如下关系:

式中:D 为分形维数。
式(1)也可以写成:
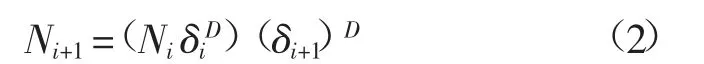
根据分形曲线的定义,式(2)可表示为:

式中:a 为常数。
把它推广至一般情况,可得到:

根据式(1),分形维数D 可表达为:
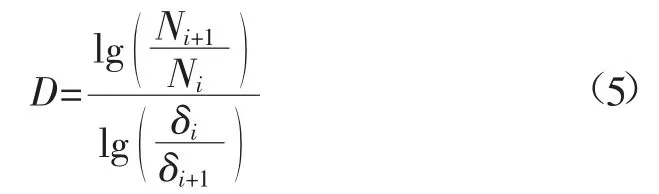
一般地,由式(4)得:

在覆盖的过程中所获得的1 组(δ,N)数据,将其画成双对数曲线图,其斜率就是该曲线的分形维数。
2.1.2 立方体覆盖法[43]
采用三维的立方体网格去直接覆盖粗糙表面,立方体覆盖法示意图如图3[44]。平面xoy 上的有1 个尺寸为δ 的正方形网格。正方形4 个角点的高度分别为h(i,j)、h(i,j+1)、h(i+1,j)以及h(i+1,j+1)(其中i≥1,j≤n-1,n 是每个边的量测点数)。
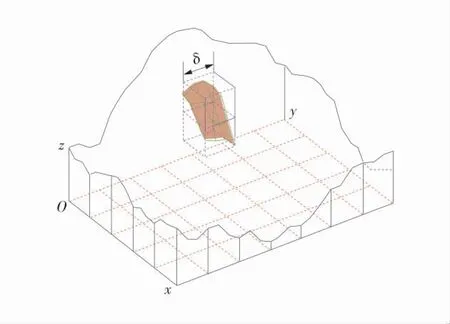
图3 立方体覆盖法示意图Fig.3 Schematic diagram of cube overlay method
用边长为δ 的立方体覆盖粗糙的表面,计算覆盖区域δ×δ 内总共有多少个立方体数,即在第(i,j)个网格内,覆盖粗糙面的立方体个数Ni,j为:
Ni,j=INT(1/δ(max(h(i,j),h(i,j+1),h(i+1,j),
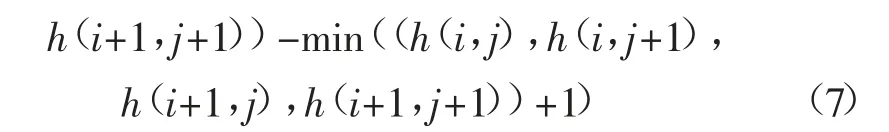
式中:INT 为取整函数。
整个粗糙面被覆盖所需要的立方体总数N(δ)为:

改变立方体尺寸再次覆盖,并计算出整个粗糙面被覆盖所需的立方体总数,如果粗糙面具有分形的性质,则根据分形理论,立方体总数N(δ)与尺寸δ 之间存在着以下的关系:

式中:D为粗糙表面的分形维数。
将粗糙面进行扫描重构,针对所获得的数据,将上述过程编写程序,建立N(δ)与尺寸δ 之间的关系,将结果绘制为立方体边长和立方体数量的双对数曲线,直线的斜率的相反数就是分形维数。
2.2 裂隙截面迹线分形各向异性特征
裂隙截面迹线是垂直于裂隙面的平面旋转不同的角度与裂隙面相交得到的曲线。将处理过的裂隙面导入Geomagic Studio 软件中,沿着裂隙扩展方向构建垂直于裂隙面的平面1-1,与裂隙面相交得到1 条迹线,并将平面1-1 逆时针旋转角度30°、45°、60°、90°、120°、135°、150°,分别对应平面2-2、3-3、4-4、5-5、6-6、7-7、8-8,共计8 个平面,与裂隙面相交得到不同角度的迹线。截面5-5 即为垂直于裂隙扩展方向的截面。截面迹线图如图4。将所得的截面迹线以点数据的形式进行保存,利用Matlab 计算分析裂隙面的分形各向异性特征。
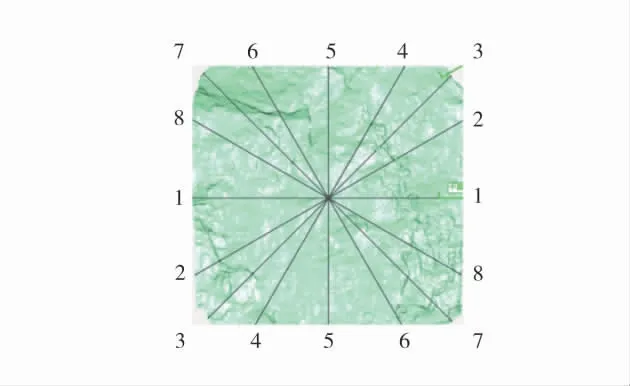
图4 截面迹线图(以T37 为例)Fig.4 Sectional trace line(Take T37 as an example)
复杂加卸载实验破坏下煤岩裂隙面截面迹线的空间展布情况如图5。
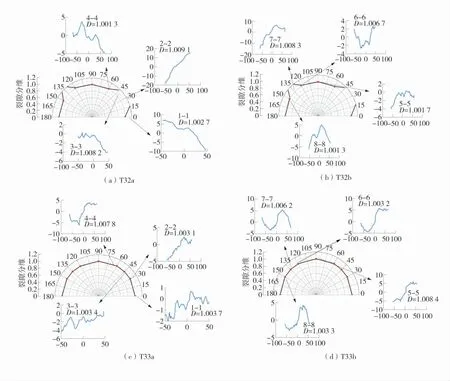
图5 复杂破坏裂隙面截面迹线空间展布及分形各向异性特征Fig.5 Spatial distribution and fractal anisotropy characteristics of cross section trace lines in fracture plane with complex failure
从各试件的截面迹线展布情况来看,迹线起伏幅度较为明显,局部空间波动幅度与高度起伏频率基本一致。以T32、T33 为例,对于T32 裂隙面来说,从截面迹线的分形维数计算结果来看,分形维数变化范围为1.001 3~1.009 1,分维最大值是最小值的1.007 8 倍。沿裂隙扩展方向逆时针旋转30°的方向,截面迹线的分维明显高于其他方向,表明沿这个方向的裂隙面破坏较为严重,粗糙程度较大。其它方向的截面迹线分维大小不一,说明复杂路径破坏形成的裂隙面形貌起伏特征不均匀,各向异性特征明显;对于T33 裂隙面,其分维最大值出现在垂直于裂隙扩展方向也就是90°方向,分维为1.008 4,最小值为1.003 1,出现在30°方向,说明裂隙面沿30°方向裂隙面相对平缓。该裂隙面截面迹线分维最大值是最小值的1.005 3 倍,各向异性特征相对明显。
从以上数据可以看出:①复杂应力路径破坏下各试件的分维波动较大,分维范围在1.001 3~1.009 6,表明破坏裂隙面表面较为粗糙,起伏特征明显;②复杂应力路径破坏裂隙面截面迹线分维最大值均出现在沿裂隙扩展方向30°~90°之间,分维最小值分布较为分散;③各裂隙面的各向异性度K 值分别是K1=1.007 8,K2=1.005 3,K3=1.007 5,可以看出各向异性度在1.005 3~1.007 8 之间,表明复杂应力路径破坏裂隙面的截面迹线分形各向异性特征较为明显。
因为LISP架构具有较好的隧道封装机制,因此它能够更好地实现网络虚拟化。对此,本文设计了一种基于LISP架构来实现网络虚拟化的优化方案。该优化方案主要对隧道路由器进行了一定的变动,并在其端口上新增了访问控制列表,以此来建立虚拟网络。本文主要介绍了两种类型的网络虚拟化优化方案。
不同方向的截面迹线分维计算结果见表3。D下标代表角度,如D0表示0°方向的截面迹线分维,以此类推。

表3 复杂应力路径破坏裂隙面截面迹线分维Table 3 Fractal dimension of cross section trace line of fracture surface damaged by complex stress path
2.3 裂隙截面分形各向异性特征
裂隙截面是沿着不同的角度在裂隙面上截取一定范围的区域。将处理过的裂隙面形貌数据点信息导入CATIA 软件中进行处理,利用扫描点重构三维断面形貌。通过对各试件复杂应力路径下破坏裂隙面共截取了12 个20 mm×20 mm 的正方形区域,其中,由于T32 煤样边界破损较为严重,为使截取的区域完整不影响结论,T32 截取的正方形形心距原心30 mm,T33 和T37 试件截取的正方形区域形心距原点为35 mm。将裂隙扩展方向设为0°,以裂隙扩展方向逆时针旋转0°、30°、60°、90°、120°、150°、180°、210°、240°、270°、300°、330°共截取了12 个区域。其中,0°为裂隙扩展方向,90°垂直于裂隙扩展方向。将截取的区域以ASC 文件形式进行保存以后,利用Matlab 编程计算各区域的分形维数。以T32 为例,截取区域以及各区域重构展布情况及分形各向异性特征如图6。

图6 复杂应力路径破坏裂隙面区域空间展布情况及各向异性特征Fig.6 Spatial distribution and anisotropy characteristics of fracture surface area damaged by complex stress path
图6 较好地展示了复杂应力路径下破坏裂隙面的空间展布情况,从图中可以看出各区域的空间波动幅度较大,与图2 表现出的破坏裂隙面起伏高低分布大致是一致的。从裂隙截面区域的分形维数计算结果可以看出,不同方向截面区域分维存在一定的差异性。
为了更加直观地看出剪切裂隙面各区域的分形维数特征,将各区域分维利用Origin 软件绘制得出分形各向异性特征图如图7。
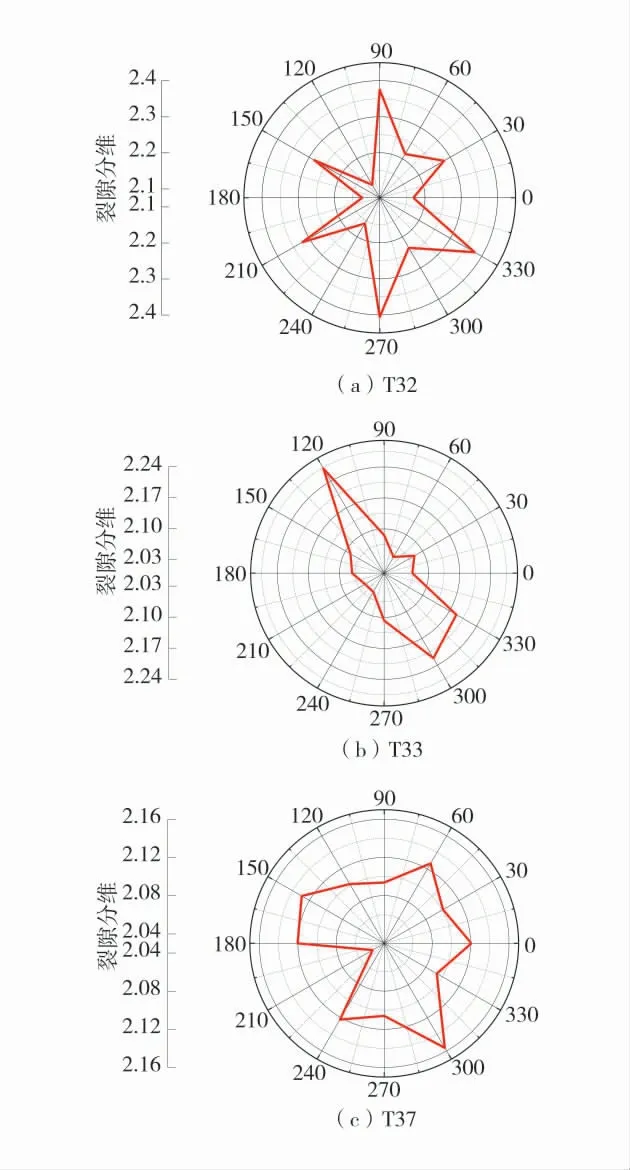
图7 典型复杂应力路径破坏面不同角度分维Fig.7 Fractal dimension of different angles of failure surface of typical complex stress path
从图7 中可以看出,对于T32,分形维数最大值为2.405 5,出现在270°的区域,最小值为2.116 5,出现在120°的区域。T33 的分形维数最大值在120°的位置,为2.273 4,最小值出现在60°区域,为2.042 3。T37 出现分维最大值的区域为300°,数值为2.156 3,最小值出现在210°区域,分维为2.044。总的来说:①复杂应力路径破坏裂隙面截面区域分形维数最大值集中在120°~300°之间,且数值明显高于其他区域分维。分维最小值集中在60°~240°区间;②将分形维数最大值与分形维数最小值的比值定义为各向异性度K,K1=1.137,K2=1.113,K3=1.055。从各向异性度可以看出,复杂应力路径破坏裂隙面的各向异性特征明显。
3 裂隙面分形特征的尺寸效应
3.1 裂隙面断面形貌截取
将处理过的裂隙面形貌特征数据导入Catia 软件中进行处理,利用扫描点重构三维断面形貌。以裂隙面质心为原点,截取同样以该原点为中心的不同大小的正方形区域,分别截取1 mm×1 mm、2 mm×2 mm、4 mm×4 mm、8 mm×8 mm、16 mm×16 mm、32 mm×32 mm、64 mm×64 mm 以及90 mm×90 mm 的8个正方形区域。尺效应过程图如图8。

图8 尺效应过程图(以T36 为例)Fig.8 Process diagram of foot-effect(take T36 as an example)
3.2 裂隙面分维尺寸效应
对绘制的区间进行切割以后以ASC 文件格式分别保存,同时利用计算面分维的Matlab 编程生成各区域的重构图,并计算分形维数值。对不同区域进行编号,如T32 所截区域1 mm×1 mm、2 mm×2 mm、4 mm×4 mm 被编为T32-1,T32-2,T32-4,以此类推。各区域的分形维数计算结果见表4。
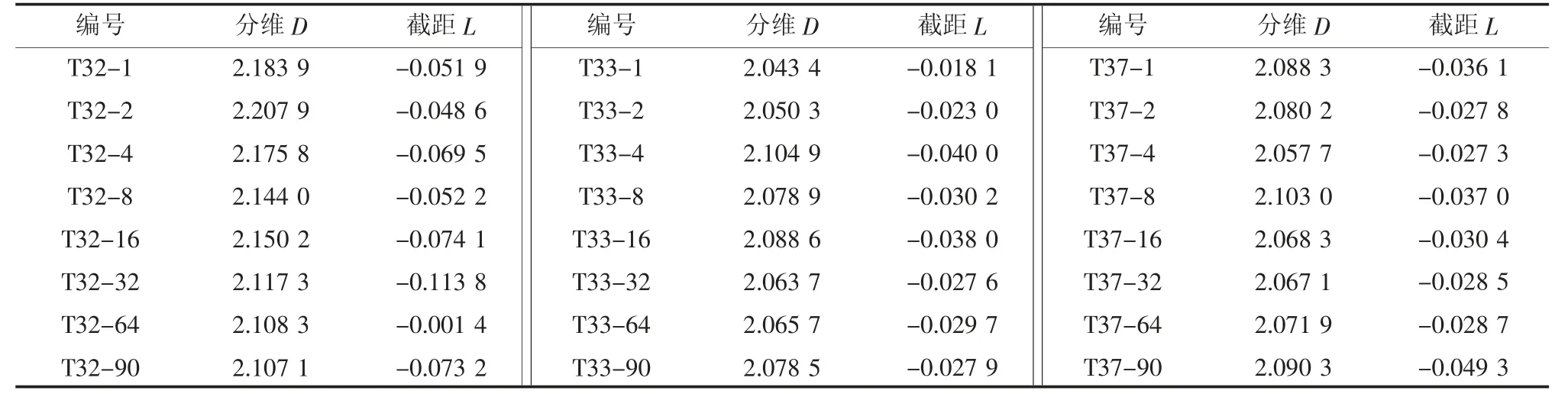
表4 尺寸效应不同区域分维Table 4 Fractal dimension of different regions of size effect
将各试件不同大小的区域分维绘制于1 张图表中,得到典型复杂应力路径破坏裂隙面不同尺寸分维变化如图9。
从图9 中可以看出,各试件在尺寸较小时,分维不太稳定。单独来看,T32 的分维最大值为2.207 9,分维最小值为2.107 1,最大值是最小值的1.049倍,尺寸效应特征相对明显;T33 的分维最大值是2.104 9,最小值为2.043 4,分维最大值是最小值的1.030 倍,随尺寸变化分维波动不大;对T37 来说,其分维最大值为2.103,最小值是2.0577,其分维最大值是最小值的1.022 倍,尺寸效应特征也不明显。对于复杂破坏路径下的破坏裂隙面,分维最大值与最小值的比值集中在1.022~1.049,随着尺寸变化,分形特征变化的规律明显。复杂应力路径破坏裂隙面分维最大值均出现在尺寸为8 mm 以内的区域,当尺寸取的比较小即边长小于20 mm 的情况下,分维波动幅度范围很大,但当所取区域边长大于20 mm 时,分维相对比较稳定。因此,对裂隙面分析分维时,采用大于20 mm 的尺寸,分维更为稳定。
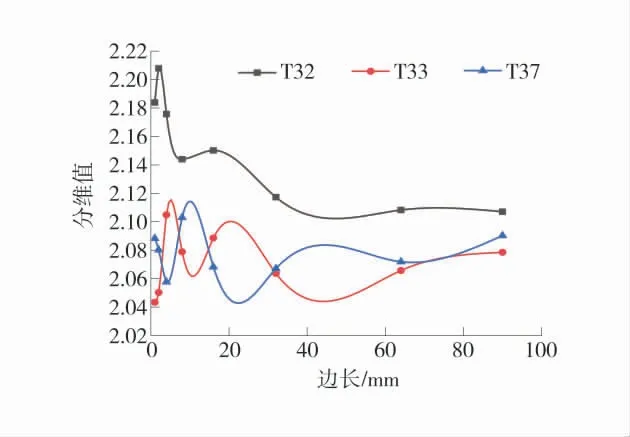
图9 典型复杂应力路径破坏裂隙面不同尺寸分维变化Fig.9 Fractal changes of different sizes of fracture surfaces in typical complex stress paths
4 结 论
1)复杂破坏裂隙面的高度起伏分布区间为1~15 mm,其空间起伏分布情况基本符合正态分布。根据裂隙面扫描形貌图可认为复杂破坏过程主要以沿晶断裂耦合穿晶断裂的形式为主,导致裂隙结构差异性明显。
2)复杂应力路径破坏下各试件的分维范围在1.001 3~1.009 6,截面迹线分维最大值均出现在沿裂隙扩展方向30°~90°之间,分维最小值分布较为分散,各裂隙面的各向异性度在1.005 3~1.007 8 之间,表明复杂应力路径破坏裂隙面的截面迹线分形各向异性特征较为明显。
3)复杂应力路径破坏裂隙面截面区域分形维数最大值集中在120°~300°之间,且数值明显高于其他区域分维,分维最小值集中在60°~240°区间。且从各向异性度可以看出,复杂应力路径破坏裂隙面的各向异性特征明显。
4)对于复杂破坏路径下的破坏裂隙面,分维最大值与最小值的比值集中在1.022~1.049,随着尺寸变化,分形特征变化的规律明显。且复杂应力路径破坏裂隙面分维最大值均出现在尺寸为8 mm 以内的区域。
5)对裂隙面分析分维时,采用大于20 mm 的尺寸,分维更为稳定。

