高速铁路道岔数控龙门铣床的多目标优化

关英俊，张 宇，习兴华，张超杰

（长春工业大学机电工程学院，吉林 长春 130012）

1 引言

近年来高铁行业发展迅速，其中高速铁路道岔作为铁路轨道的重要组成部分，其加工制造也得到越来越多的关注。高速铁路道岔通常使用高锰钢材料制成，加工难度较大，并且高速铁路道岔通常采用成型铣刀一次加工成型，属于重切削类型，因此对加工设备有较高的要求。高速铁路道岔数控龙门铣床作为加工设备，应具有稳定的机械结构以及足够高的动静态刚度和抗振性能，这样才能满足高速铁路道岔的加工需求。

随着数字化设计技术的发展，优化方法也在不断的进步。文献[1]对加工中心床身尺寸元结构的优化进行了研究，在加工中心床身结构质量减小的情况下改善了其动态性能。文献[2]基于试验设计的响应面法，对TK6920型数控落地镗铣床的床身结构进行优化设计并得到最优解。文献[3]提出了一种基于遗传算法的锻压机床优化设计方法，基于该方法开发了一个以多目标参数优化系统为核心的优化设计平台，并验证了平台的有效性与可靠性。文献[4]对同步双驱精密卧式加工中心做了灵敏度分析与多目标优化，采用层次分析法筛选出了最优解。文献[5]对DL-20MP型数控机床床身进行基于灵敏度分析的尺寸优化设计，提高了床身的动态特性。文献[6]对DL20MST型数控车床的床鞍进行了基于神经网络响应面法的尺寸优化，降低了床鞍的质量。

数控龙门铣床具有较为复杂的结构，且影响机床稳定性的因素较多，从而需要从各个方面入手进行优化研究。多数研究人员只对单个因素进行分析优化，这往往不能满足设计需求。因此以高速铁路道岔数控龙门铣床的结构作为研究对象，通过灵敏度分析找出机床结构的关键设计尺寸，并采用多目标尺寸优化的方法对其结构进行改进。

2 建模

运用SolidWorks软件对高速铁路道岔数控龙门铣床进行建模。机床结构主要由立柱、横梁、十字滑座、滑枕、主轴箱、底座、工作台等构成，其中底座和工作台单独安装在地面上，所以在有限元建模和后续的优化中不包括这两部分。运用HyperMesh软件对简化后的机床模型进行网格划分，共划分31845 个节点、31994个单元。

数控龙门铣床大件的材料为灰铸铁HT300，弹性模量为130GPa，泊松比为0.25，密度为7400kg/m3。在整机模型中，当主轴组件所在位置不同时，机床所承受的力和发生的形变不同，根据力学理论可知当主轴组件位于横梁中间时横梁的刚度最弱，故本次分析选择了此工况，约束定义为立柱底面和地面接触的部分施加全约束。三维模型，如图1所示；有限元模型，如图2所示。

图1 三维模型Fig.1 Three-Dimensional Model

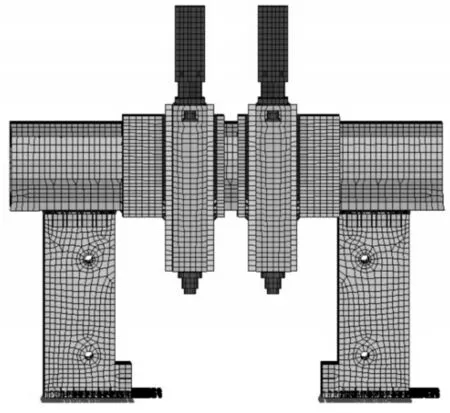
图2 有限元模型Fig.2 Finite Element Model

3 多目标优化数学模型

在设计过程中，以单个目标做优化有时不能满足设计需求；而以多个目标独立地做优化时，各个目标之间有时会产生冲突，不能同时满足设计需求。比如在求解时，需要将柔度最小化且固有频率最大化，结果往往会发生这样的情况：当柔度最小时，固有频率不是最大；又或者固有频率最大时，柔度达不到最小。当优化的各个目标有冲突时，很难求得最优解，于是在这里引入折衷规划法进行求解多目标优化。

折衷规划法的目的是把多个目标通过函数合理的转换成一个单独的目标，进而直接对单目标做优化。最终得到既满足柔度最小又能保证1阶固有频率最大的数学模型如下[7]：

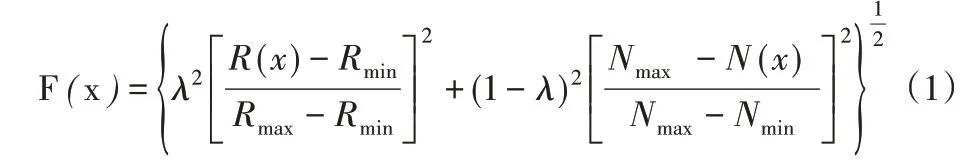
式中：F(x)—综合目标函数；R(x)—柔度目标函数；N(x)—平均频率；λ—柔度的权重，设为0.4；1-λ—固有频率的权重，为0.6；Rmin、Rmax—柔度的最小值与最大值；Nmin、Nmax—1 阶固有频率的最小值与最大值。

若要进行多目标优化求解，还需优先计算出柔度和1阶固有频率的最大值与最小值。求解方法：首先通过灵敏度分析求得数控龙门铣床结构的关键尺寸，然后选取关键尺寸做单工况单目标尺寸优化，最后由优化结果可得柔度与1阶固有频率的数值。

4 灵敏度分析

灵敏度分析是研究系统状态变化对系统参数敏感程度的一种方法。利用灵敏度分析可求得尺寸变化对固有频率、质量等参数的影响程度，进而从中获取关键的设计尺寸，为后续的优化设计提供参考。运用HyperMesh软件中的Sensitivity卡片对数控龙门铣床做灵敏度分析：以机床各个零件的壁厚、筋板厚作为设计变量，以机床的质量和第1、2阶固有频率作为性能指标。其中各个变量的结构位置，如图3所示。各个变量的尺寸变化范围，如表1所示。灵敏度分析所得结果，如图4～图6所示。

图3 尺寸位置简图Fig.3 Schematic Diagram of Size and Location

表1 尺寸变化范围Tab.1 Size Range

灵敏度图中，在零刻度线以上，结构的性能随着设计变量的增加而增大；反之，在零刻度线以下，结构的性能随着设计变量的增加而减小。由图4对质量灵敏度的分析可知，C1、C5、C6、C7的尺寸对质量影响最大；C3、C4、C8、C11、C17、C18、C19的尺寸对质量影响次之；其余尺寸对质量几乎无影响。

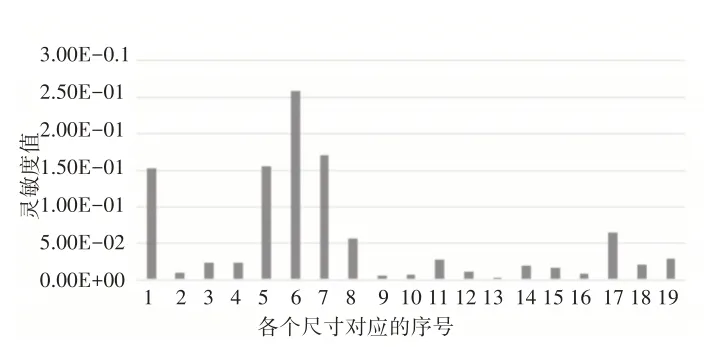
图4 对质量灵敏度分析Fig.4 Mass Sensitivity Analysis

由图5对1阶固有频率灵敏度的分析可知，C1、C5、C6、C7、C17 的尺寸对1 阶固有频率影响最大，C4、C11、C14、C15、C16、C18、C19的尺寸对1阶固有频率影响次之，其余尺寸对1阶固有频率几乎无影响。由图6对2阶固有频率灵敏度的分析可知，C1、C5、C6、C17 的尺寸对2 阶固有频率影响最大，C4、C7、C11、C14、C15、C16、C18、C19的尺寸对2阶固有频率影响次之，其余尺寸对2阶固有频率几乎无影响。最终取C1、C4、C5、C6、C7、C11、C14、C15、C16、C17、C18、C19作为关键尺寸，为后续优化做准备。

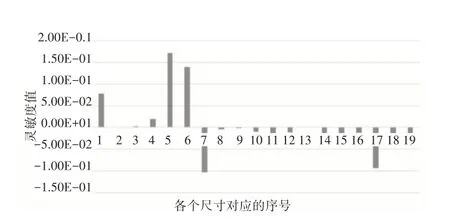
图5 对1阶固有频率灵敏度分析Fig.5 Sensitivity Analysis of First Order Natural Frequency

图6 对2阶固有频率灵敏度分析Fig.6 Sensitivity Analysis of Second Order Natural Frequency

为了使机床结构变形最小，通常以结构的刚度最大化为目标进行优化。在处理这类问题时，往往把刚度最大化问题等效为柔度最小化问题来解决[8]。

在静态单工况条件下，以机床各个零件的壁厚、筋板厚C1、C4、C5、C6、C7、C11、C14、C15、C16、C17、C18、C19作为设计变量，设体积分数0.3为约束条件，柔度最小为目标函数。通过Hyper-Mesh软件中的OptiStruct模块对机床进行尺寸优化。

优化求解后由OUT文件得到最小柔度Rmin=5928.78J，最大柔度Rmax=8514.16J，为后续多目标优化做准备。

固有频率仅与系统的质量、形状、材料等固有特性有关。其中高阶固有频率的振幅一般较小，对结构的影响也较小；而低阶固有频率的振幅一般较大，更容易使结构发生共振。因此提高机床的低阶固有频率对于改善结构的动态稳定性能具有重要意义。

若要得到机床固有频率的初值和最大值，可通过尺寸优化进行求解。在优化求解的过程中，可能会出现模态交换现象，从而使目标函数之间产生振荡问题。为了克服这一问题，采用平均频率公式定义固有频率的数学模型如下所示[9-10]：

式中：N(x)—平均频率；λi—第i阶特征频率；α、β—设定参数，用来调整目标函数；μi—第i阶频率权重系数；m—需要优化的频率阶次。

通过HyperMesh 软件中的OptiStruct 模块对机床进行尺寸优化。在动态单工况条件下，以机床各个零件的壁厚、筋板厚C1、C4、C5、C6、C7、C11、C14、C15、C16、C17、C18、C19作为设计变量，设体积分数0.3为约束条件，以1阶固有频率最大化为目标函数进行尺寸优化。优化求解后由.OUT文件得到1阶固有频率的最小值Nmin=29.56Hz，最大值Nmax=34.87Hz，为后续多目标优化做准备。

5 多目标优化的求解

运用OptiStruct 软件对高速铁路道岔数控龙门铣床进行多目标优化。由于OptiStruct模块本身不支持多目标的尺寸优化，所以需要用OptiStruct模块的函数自定义功能，将多目标优化的数学模型转化为function类型的响应，且通过function响应关联两种单工况，最终将function响应作为此次多目标优化的目标函数。function类型响应如下：

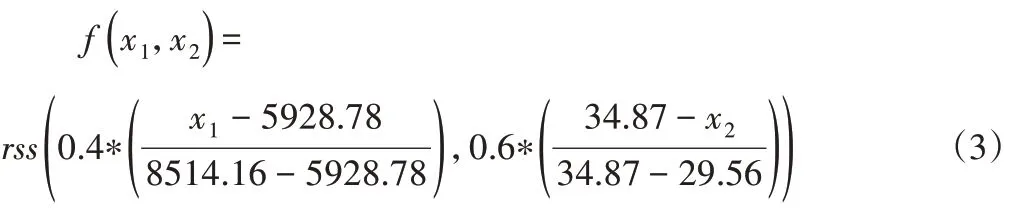
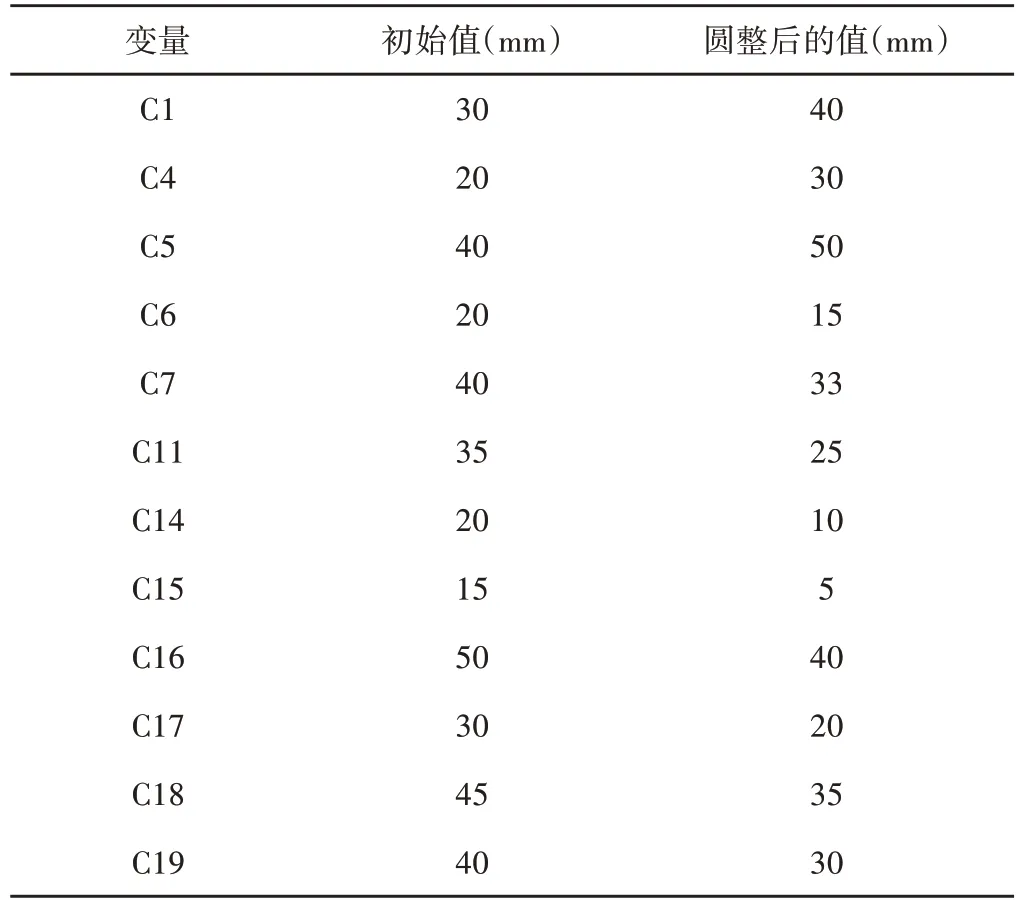
表2 尺寸圆整结果Tab.2 Size Roundness Results

根据多目标优化所得尺寸重新建立有限元模型，并通过模态分析计算出新的1、2阶固有频率结果，如图7、图8所示。优化后的1 阶固有频率为34.99Hz，比优化前的1 阶固有频率提高了18.4%；优化后的2 阶固有频率为38.89Hz，比优化前的2 阶固有频率提高了17.1%；优化后的柔度为6199.47J，比优化前的柔度降低了27.2%；优化后的质量为36.35t，比优化前的质量降低了4.0%。对比结果，如表3所示。

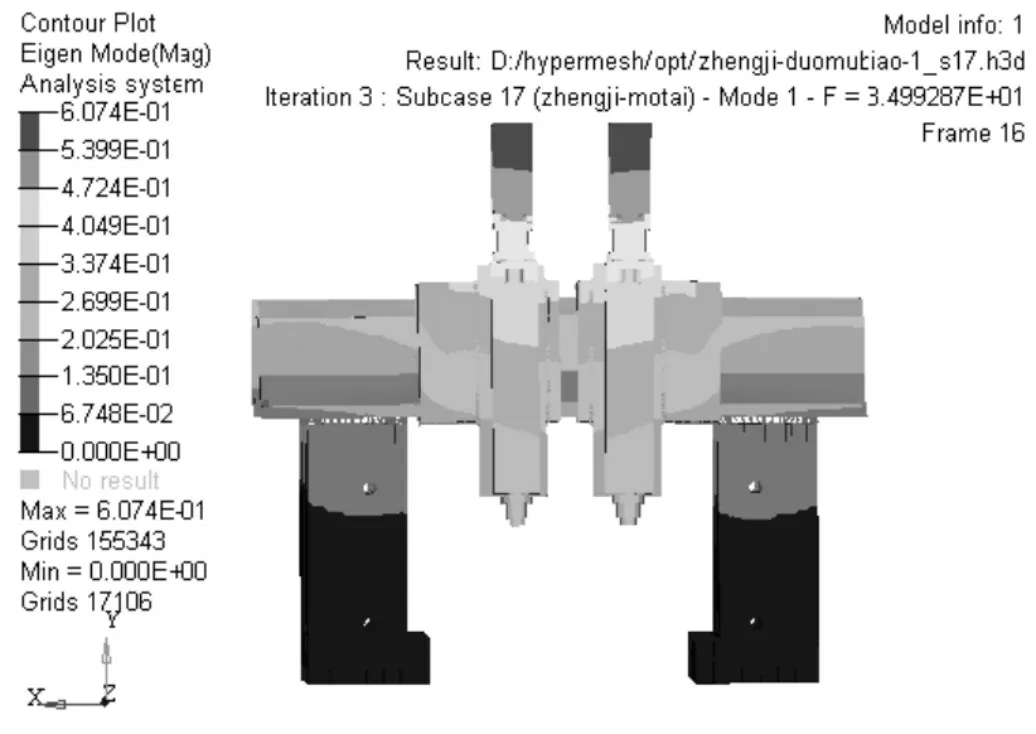
图7 1阶模态Fig.7 First-Order Modal

图8 2阶模态Fig.8 Second-Order Modal

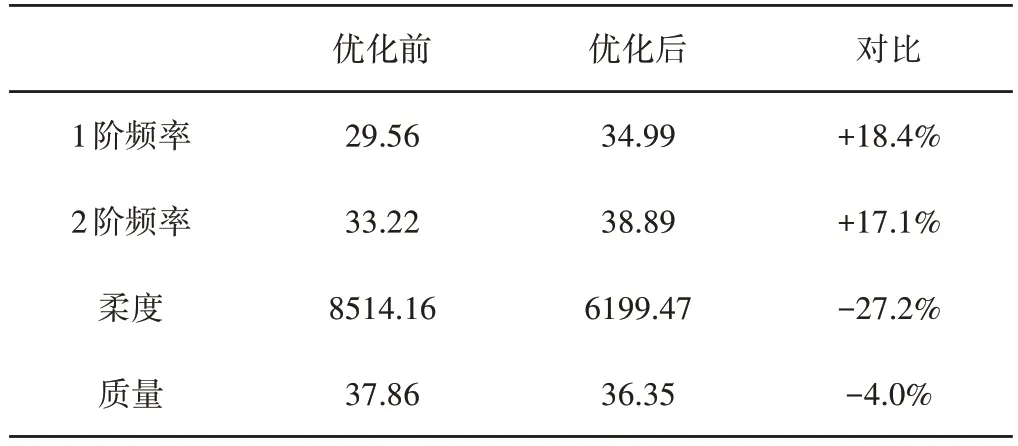
表3 优化结果Tab.3 Optimized Result

6 结论

利用HyperMesh软件建立了高速铁路道岔数控龙门铣床的有限元模型。通过灵敏度分析寻找到机床结构的关键尺寸，并对其进行了静态刚度优化和固有频率优化，随后利用折衷规划法将柔度和固有频率组合成新的函数，对其进行了多目标尺寸优化，优化后使机床1阶固有频率提高了18.4%，2阶固有频率提高了17.1%，柔度降低了27.2%，质量降低了4.0%，优化效果良好。此优化设计思路可为同类产品的设计提供参考与借鉴。